代码随想录第四天 | 链表：模拟（leetcode 24）；双指针在链表上的应用（leetcode 19, 160, 142）

1、正常模拟

1.1 leetcode 24

第一遍代码：写的是没有采用虚拟头节点的情况

看示例的图片，考虑怎么转换，对于节点->next修改如果之后要用这个节点的下一个节点要注意之前操作对于这个下一个节点的变化或者设个值暂存，如果只是修改这个节点本身（不包括对其next的修改）对于下一个节点的使用没事。

改节点的时候要考虑这个节点的数据要不要找个变量存一下，对于指针改变操作的顺序都可以写

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* cur = head;
        ListNode* pre;
        ListNode* nextnode;
        if(head == nullptr || head->next == nullptr) {
            return head;
        }
        else {
            nextnode = head->next->next;
            cur = head->next;
            cur->next = head;
            head->next = nextnode;
            pre = head;
            head = cur;
            cur = nextnode;
        }
        while(cur != nullptr && cur->next != nullptr) {
            pre->next = cur->next;
            pre = cur;
            nextnode = cur->next->next;
            cur->next->next = cur;
            cur->next = nextnode;
            cur = nextnode;
        }

        return head;
    }
};

一定要画图，不画图，操作多个指针很容易乱，而且要想明白操作的先后顺序

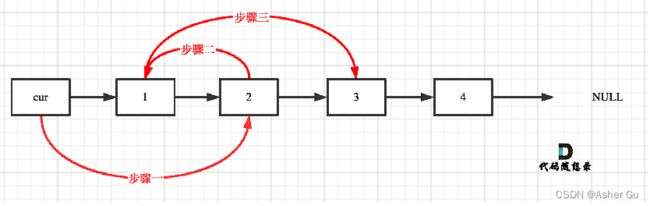
1.2 虚拟节点使用条件，画图分析操作过程

因为牵扯到对两个交换节点之前的元素的操作，所以要加个虚拟节点。有虚拟头节点的情况：（[1], [2], [3]为三次变换）

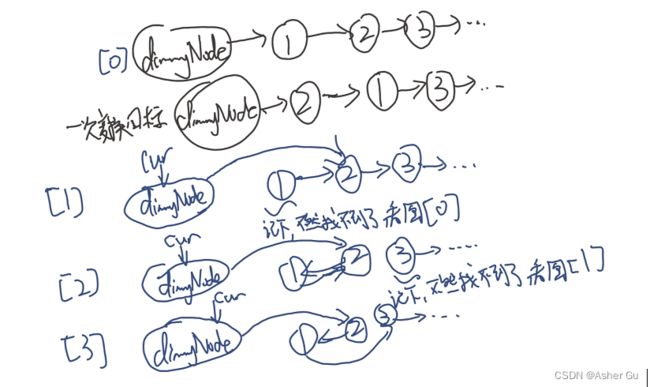
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dimmynode = new ListNode(0);
        dimmynode->next = head;
        ListNode* cur = dimmynode;
        ListNode* pre;
        ListNode* next;
        while(cur->next != nullptr && cur->next->next != nullptr) {
             next = cur->next;
             cur->next = cur->next->next;//发现原来的1号位可能找不到了，要记下（上一行代码）
             //[1]
             pre = cur->next->next;//记录3号位，看第一步改动完成的图
             cur->next->next = next;
             //[2]
             cur->next->next->next = pre;
             //[3]
             cur = cur->next->next;//最后别忘了把cur移动到1号位(不是3号位)
        }
        return dimmynode->next;
    }
};

2、双指针

主要包括快慢指针（从后往前适用，因为链表只能从前往后），以及加入数学计算

2.1 leetcode 19：滑动窗口

删除节点明显要用到前一个节点，所以需要设置虚拟指针。第一次代码：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
    //删除节点明显要用到前一个节点，所以需要设置虚拟指针
        ListNode* dimmynode = new ListNode(0);
        dimmynode->next = head;
        //利用滑动窗口思想找到倒数第N个节点，因为链表只能从前往后，由于删除节点需要找到前一个结点，所以双指针滑动窗口大小为n+1，从虚拟头节点开始
        ListNode* start = dimmynode;
        ListNode* end = dimmynode;
        int len = 1;
        while(len < n+1) {//因为start==end就是长度为1了，所以只要走n步长度就能为n+1
            end = end->next;
            len++;
        }
        while(end->next != nullptr) {
            start = start->next;
            end = end->next;
        }
        ListNode* pre = start;
        ListNode* cur = start->next;
        
        pre->next = pre->next->next;
        delete cur;//如果是最后删除成为空指针时如（[1]，1），如果返回head就是空值了，应该返回dummynode->next
        return dimmynode->next;
    }
};

end首先走n + 1步 ，为什么是n + 1呢，因为只有这样同时移动的时候start才能指向删除节点的上一个节点（方便做删除操作)

2.2 leetcode 160：swap函数

第一次代码：

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        //双指针，因为相当于找是否有节点重合（不止元素相等，是指针相等），除了倒转外，就想到数个数
        ListNode* as = headA;
        ListNode* bs = headB;
        //由于链表只可能在后面重合，所以在两个链表在距离末尾相同的位置开始往后走即可
        //先让a,b走到距末尾相同的位置，参考leetcode 19滑动窗口思想找末尾的
        ListNode* ae = headA;
        ListNode* be = headB;
        int asize = 0;
        int bsize = 0;
        while(ae != nullptr) {
            ae = ae->next;
            asize++;
        }
        while(be != nullptr) {
            be = be->next;
            bsize++;
        }
        if(asize > bsize) {
            int gap = asize - bsize;
            while(gap--) {
                as = as->next;
            }
        }
        else {
            int gap = bsize - asize;
            while(gap--) {
                bs = bs->next;
            }
        }
        while(bs != as) {
            bs = bs->next;
            as = as->next;//考虑as/bs为空的时候的特殊的情况也符合
        }
        return bs;
    }
};

可以用swap函数避免asize和bsize（分别为两个链表的长度）谁大谁小分两种情况考虑

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != NULL) { // 求链表A的长度
            lenA++;
            curA = curA->next;
        }
        while (curB != NULL) { // 求链表B的长度
            lenB++;
            curB = curB->next;
        }
        curA = headA;
        curB = headB;
        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            swap (lenA, lenB);
            swap (curA, curB);
        }
        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上（末尾位置对齐）
        while (gap--) {
            curA = curA->next;
        }
        // 遍历curA 和 curB，遇到相同则直接返回
        while (curA != NULL) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

2.3 leetcode 142（未能找到入口）

第一次代码：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        //看有没有环，首先想到双指针。而又因为需要有环一定要相遇，所以快的那个指针一次走两格
        //而快的指针一定比慢的多走环的整数圈，就可以知道圈有多大，但是不知道什么时候是圈子的起点

    }
};

动图与思路来源 代码随想录

不仅考察对链表的操作，而且还需要一些数学运算。

主要考察两知识点：
判断链表是否环（思路与第一遍代码相同）
如果有环，如何找到这个环的入口

2.4 判断链表是否有环

可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环（追及问题）

2.5 如何找到这个环的入口

假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示：

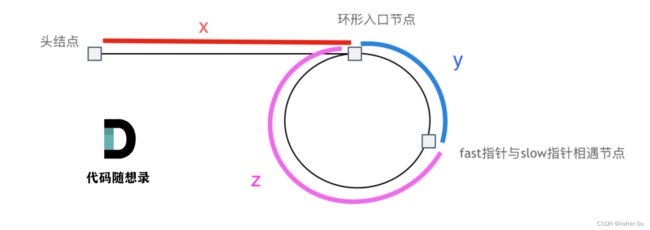
那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针， （y+z）为 一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点， 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

两边消掉一个（x+y）: x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示 头结点到 环形入口节点的的距离。

所以要求x ，将x单独放在左面：x = n (y + z) - y ,

再从n (y + z) 中提出一个 （y + z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针

再把z移过去，
x - z = (n - 1) (y + z)，
意味着x和z之间差 >= 0圈

也就意味着从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

修改代码（注意while逻辑）

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while((fast != nullptr && fast->next != nullptr) ) {
            //fast == slow不能放在while里，因为开始的时候都是head所以跳出去了
            slow = slow->next;
            fast = fast->next->next;
            if(fast == slow) {
                slow = head;
                while(slow != fast) {
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }
        return nullptr;
    }
};

时间复杂度: O(n)，快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
空间复杂度: O(1)

利用快指针和慢指针速度的两倍关系，可以考虑极端情况

2.6 利用极端情况考虑问题

为什么第一次在环中相遇，slow的 步数 是 x+y 而不是 x + 若干环的长度 + y 呢？
首先slow进环的时候，fast一定是先进环来了。

如果slow进环入口，fast也在环入口（

fast和slow同时在入口，是fast追赶slow最极端的情况，追整整一圈，但凡fast不在入口处，追赶一定在入口处的slow都不用走那么费劲

），那么把这个环展开成直线，就是如下图的样子：

可以看出如果slow 和 fast同时在环入口开始走，一定会在环入口3相遇，slow走了一圈，fast走了两圈
slow进环的时候，fast一定是在环的任意一个位置，如图：

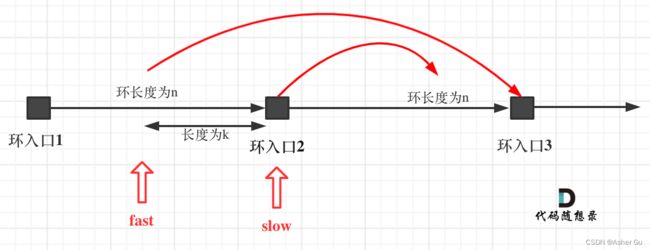
那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。

因为k是小于n的（图中可以看出），所以**(k + n) / 2 一定小于n**。

也就是说slow一定没有走到环入口3，而fast已经到环入口3了。

在slow开始走的那一环已经和fast相遇了。

为什么fast不能跳过去呢？ 在刚刚已经说过一次了，fast相对于slow是一次移动一个节点，所以不可能跳过去。