XGBoost实战2--数据预测保险赔偿
一、概述
本次实战基于给出的数据进行保险预测。数据集:Allstate Claims Severity | Kaggle
给出的训练数据是116列(cat1-cat116)的离散数据和14列(con1-con14)的连续数据。数据集中的每一行表示一个保险索赔。必须预测‘loss’列的值。
二、导入包
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pyecharts.charts import Bar
import pyecharts.options as opts
from scipy import stats
import seaborn as sns
import xgboost as xgb
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer三、查看数据
1、 info查看数据类型
train_data = pd.read_csv('./allstate-claims-severity/train.csv')
test_data = pd.read_csv('./allstate-claims-severity/test.csv')
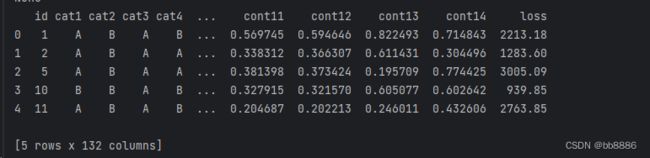
print(train_data.info())2、head查看数据前5条信息
print(train_data.head())3、shape查看数据大小
print(train_data.shape)4、查看数据列名
print('前20列名:', list(train_data.columns[:20]))
print('后20列名:', list(train_data.columns[-20:]))5、describe查看数据统计量信息
print(train_data.describe())6、查看数据是否有空值
print(pd.isnull(train_data).values.any()) # False表示没有缺失值pandas的any方法
7、统计离散型和连续型变量的数量
cat_features = list(train_data.select_dtypes(include=['object']).columns)
print('离散型特征有{}个,它们是:{}'.format(len(cat_features), cat_features))
cont_features = [cont for cont in list(train_data.select_dtypes(include=['float64']).columns) if cont not in ['loss']]
print('连续型特征有{}个,它们是:{}'.format(len(cont_features), cont_features))pandas的selectdtypes方法
8、离散型特征
(1)统计每一类离散型数据的数目
cat_uniques = {}
for cat in cat_features:
cat_uniques[cat] = len(list(train_data[cat].unique()))
cat_uniques_df = pd.DataFrame({'cat_name':list(cat_uniques.keys()),
'unique_values': list(cat_uniques.values())})
print(cat_uniques_df)
data = cat_uniques_df['unique_values'].value_counts().to_dict()
bar = Bar()
bar.add_xaxis(list(data.keys()))
bar.add_yaxis('', list(data.values()))
bar.set_global_opts(title_opts=opts.TitleOpts(title='离散特征值分布情况', pos_left='center'),
xaxis_opts=opts.AxisOpts(name='离散特征中的\n不同值的数目'),
yaxis_opts=opts.AxisOpts(name='具有X个不同值的\n分类特征的数量', is_show=True, splitline_opts=opts.SplitLineOpts(is_show=True))
)
bar.render('a.html')正如我们所看到的,大部分的分类特征(72/116)是二值的,其中有一个具有326个值的特征。
(2)列举了10类离散型特征分布情况
fig, ax = plt.subplots(2, 5, figsize=(16, 9))
for i in range(2):
for j in range(5):
cat = cat_features[5*i+j]
data = train_data[cat].value_counts().to_dict()
ax[i][j].bar(list(data.keys()), list(data.values()), width=0.5)
ax[i][j].set_xlabel(cat)
plt.savefig('./g.png')9、连续型特征
(1)绘制连续值特征分布图
train_data[cont_features].hist(bins=50, figsize=(16, 12))
plt.savefig('./d.png', dpi=300)(2)特征之间的相关性
plt.subplots(figsize=(16, 9))
corr_data = train_data[cont_features].corr()
sns.heatmap(corr_data, annot=True)
plt.savefig('./e.png', dpi=300)(3) 统计连续特征与loss的相关性值,并按降序排列,绘制图
cont_features.append('loss')
res = train_data[cont_features].corr()['loss'].apply(lambda x: round(x, 4)).to_dict()
print(list(res.keys()))
bar2 = Bar()
bar2.add_xaxis(list(res.keys())[:-1])
bar2.add_yaxis('', list(res.values())[:-1], label_opts=opts.LabelOpts(formatter='{c}'))
bar2.set_global_opts(xaxis_opts=opts.AxisOpts(axistick_opts=opts.AxisTickOpts(is_inside=True), # 设置刻度线朝里还是外
axislabel_opts=opts.LabelOpts(interval=0))) # 解决pyechart x轴标签隔一个展示一个的问题
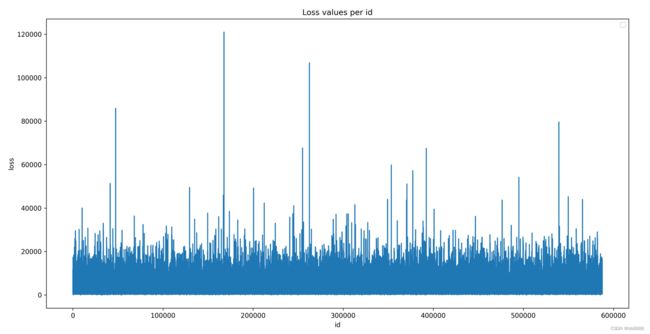
bar2.render('f.html')10、绘制loss值
plt.figure(figsize=(16, 8))
plt.plot(train_data['id'], train_data['loss'])
print('train_data[\'id\']的个数', len(train_data['id']))
plt.title('Loss values per id')
plt.xlabel('id')
plt.ylabel('loss')
plt.legend()
plt.savefig('./b.png', dpi=300)
# plt.show()11、loss的偏度
偏度:度量了实值随机变量的均值分布的不对称性,下面让我们来计算一下loss的偏度。
# scipy.stats 统计指标
skew = stats.mstats.skew(train_data['loss']).data
print(skew)
after_transform_skew = stats.mstats.skew(np.log(train_data['loss'])).data
print(after_transform_skew)
# 两种loss分布对比
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(16, 5)
ax1.hist(train_data['loss'], bins=50)
ax1.set_title('Train Loss target histogram')
ax1.grid(True)
ax2.hist(np.log(train_data['loss']), bins=50, color='g')
ax2.set_title('Train Log Loss target histogram')
ax2.grid(True)
plt.savefig('./c.png', dpi=300)
# plt.show()四、数据预处理--处理训练集和测试集
1、训练集
(1)增加log_loss作为训练集中的预测值y
train_data['log_loss'] = np.log(train_data['loss'])
train_y = train_data['log_loss'](2)选出特征作为训练集中的特征x
features = [x for x in train_data.columns if x not in ['id', 'loss', 'log_loss']]
train_x = train_data[features](3)将离散型转换为数值型
# 将目标列,转换为 category 类型;然后,转换为整形的编码
for c in range(len(cat_features)):
train_x[cat_features[c]] = train_x[cat_features[c]].astype('category').cat.codes
print(train_x)2、测试集
(1)选出特征作为测试集中的特征x
features_test = [x for x in test_data.columns if x not in ['id']]
test_x = test_data[features](2)将离散型转换为数值型
# 将目标列,转换为 category 类型;然后,转换为整形的编码
for c in range(len(cat_features)):
test_x[cat_features[c]] = test_x[cat_features[c]].astype('category').cat.codes
print(test_x)五、建立模型
1、XGBoost 参数
booster : gbtree, 用什么方法进行结点分裂。梯度提升树来进行结点分裂。
objective : multi softmax, 使用的损失函数,softmax 是多分类问题
num_class : 10, 类别数,与 multi softmax 并用
gamma : 损失下降多少才进行分裂
max_depth : 12, 构建树的深度, 越大越容易过拟合
lambda : 2, 控制模型复杂度的权重值的L2正则化项参数,参数越大。模型越不容易过拟合。
subsample : 0.7 , 随机采样训练样本,取70%的数据训练
colsample_bytree : 0.7, 生成树时进行的列采样
min_child_weight : 3, 孩子节点中最小的样本权重和,如果一个叶子结点的样本权重和小于 min_child_weight 则拆分过程结果
slient : 0, 设置成 1 则没有运行信息输出,最好是设置为0
eta : 0.007, 如同学习率。前面的树都不变了,新加入一棵树后对结果的影响占比
seed : 1000
Thread : 7, cup 线程数
2、建立xgboost模型
(1)划分数据集并将数据类型转换成库可以使用的底层格
x_train, x_test, y_train, y_test = train_test_split(train_x, train_y, test_size=0.2, random_state=14)
print(x_test)
dtrain = xgb.DMatrix(x_train, y_train)
d_test = xgb.DMatrix(x_test, y_test)(2) xgboost的CV建模
step1:初始参数
xgb_params = {
'seed': 0,
'eta': 0.1,
'colsample_bytree': 0.5,
'silent': 1,
'subsample': 0.5,
'objective': 'reg:squarederror',
'max_depth': 5,
'min_child_weight': 3
}step2:定义计算损失值的函数
评估策略:e的次幂,用来评估。
结果衡量方法:使用平均绝对误差来衡量,mean_absolute_error(np.exp(y), np.exp(yhat))。
def xg_eval_mae(y_hat, dtrain):
y = dtrain.get_label()
return 'mae', mean_absolute_error(np.exp(y), np.exp(y_hat))step3:CV建模
# feval:评估策略
bst_cv1 = xgb.cv(xgb_params, dtrain, num_boost_round=50, nfold=3, seed=0,
feval=xg_eval_mae, maximize=False, early_stopping_rounds=10)
print('CV score:', bst_cv1.iloc[-1, :]['test-mae-mean'])
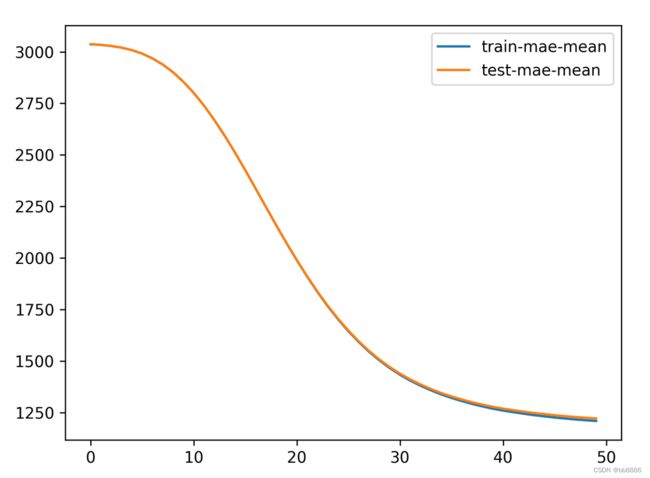
plt.figure()
bst_cv1[['train-mae-mean', 'test-mae-mean']].plot()
plt.savefig('./h.png', dpi=300)(3)修改num_boost_round参数
上面建立的树模型为50, 我们设置为100对比下结果。
bst_cv2 = xgb.cv(xgb_params, dtrain, num_boost_round=100, nfold=3, seed=0,
feval=xg_eval_mae, maximize=False, early_stopping_rounds=10)
print ('CV score:', bst_cv1.iloc[-1, :]['test-mae-mean'])绘图100个数树模型下的结果
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(16, 4)
ax1.set_title('100 rounds of training')
ax1.set_xlabel('Rounds')
ax1.set_ylabel('Loss')
ax1.grid(True)
ax1.plot(bst_cv2[['train-mae-mean', 'test-mae-mean']])
ax1.legend(['Training Loss', 'Test Loss'])
ax2.set_title('60 last rounds of training')
ax2.set_xlabel('Rounds')
ax2.set_ylabel('Loss')
ax2.grid(True)
ax2.plot(bst_cv2.iloc[40:][['train-mae-mean', 'test-mae-mean']])
ax2.legend(['Training Loss', 'Test Loss'])
plt.savefig('./i.png', dpi=300)我们把树模型的数量增加到了100。效果不是很明显。看最后的60次。我们可以看到 测试集仅比训练集高那么一丁点。存在一丁点的过拟合。
不过我们的CV score更低了。接下来,我们改变其他参数。
(4)输出当前模型下测试集的预测值
改变参数之前,需要输出当前模型下测试集的预测值,以观察模型结果有无提升。
step1:数据类型转换成库可以使用的底层格式。
dtest_x = xgb.DMatrix(test_x)step2:用XGBoost自身的库来实现(使用train)
model = xgb.train(xgb_params, dtrain, num_boost_round=50)
test_predict = model.predict(d_test)
mse = mean_squared_error(y_test, test_predict)
print(mse)step3:可输出真实的预测值
test_y = model.predict(dtest_x)
print(test_y[1], len(test_y))调优前的MSE为0.321。
2、xgboost参数调节
step1:选择一组初始参数
衡量标准
def mae_score(y_true, y_pred):
return mean_absolute_error(np.exp(y_true), np.exp(y_pred))
mae_scorer = make_scorer(mae_score, greater_is_better=False)step2:改变 max_depth 和 min_child_weight,其他参数不变
params = {
'seed': 0,
'eta': 0.1,
'colsample_bytree': 0.5,
'silent': 1,
'subsample': 0.5,
'objective': 'reg:squarederror',
# 'max_depth': 5,
# 'min_child_weight': 3,
'num_boost_round': 50,
}
cv_params = {'max_depth': list(range(4, 9)), 'min_child_weight': list((1, 3, 6))}
model = xgb.XGBRegressor(**params)
grid = GridSearchCV(estimator=model, param_grid=cv_params, scoring=mae_scorer, cv=5, verbose=1, n_jobs=4)
grid.fit(x_train, y_train)
test_predict = grid.predict(x_test)
mse = mean_squared_error(y_test, test_predict)
test_y = grid.predict(test_x)
print(grid.best_params_)
print(mse)
print(grid.best_score_)改变 max_depth 和 min_child_weight后,MSE:0.321-->0.296。
step3:调节 gamma 降低模型过拟合风险
params = {
'seed': 0,
'eta': 0.1,
'colsample_bytree': 0.5,
'silent': 1,
'subsample': 0.5,
'objective': 'reg:squarederror',
'max_depth': 8,
'min_child_weight': 3,
'num_boost_round': 50,
}
cv_params = {'gamma': [0.1 * i for i in range(0, 5)]}
model = xgb.XGBRegressor(**params)
grid = GridSearchCV(estimator=model, param_grid=cv_params, scoring=mae_scorer, cv=5, verbose=1, n_jobs=4)
grid.fit(x_train, y_train)
test_predict = grid.predict(x_test)
mse = mean_squared_error(y_test, test_predict)
test_y = grid.predict(test_x)
print(grid.best_params_)
print(mse)
print(grid.best_score_)调节gamma后,MSE:0.296-->0.297。
Step 4: 调节样本采样方式 subsample 和 colsample_bytree
params = {
'seed': 0,
'eta': 0.1,
# 'colsample_bytree': 0.5,
'silent': 1,
# 'subsample': 0.5,
'objective': 'reg:squarederror',
'max_depth': 8,
'min_child_weight': 3,
'num_boost_round': 50,
'gamma': 0.1
}
cv_params = {'subsample': [0.1 * i for i in range(6, 9)],
'colsample_bytree': [0.1 * i for i in range(6, 9)]}
model = xgb.XGBRegressor(**params)
grid = GridSearchCV(estimator=model, param_grid=cv_params, scoring=mae_scorer, cv=5, verbose=1, n_jobs=4)
grid.fit(x_train, y_train)
test_predict = grid.predict(x_test)
mse = mean_squared_error(y_test, test_predict)
test_y = grid.predict(test_x)
print(grid.best_params_)
print(mse)
print(grid.best_score_)调节样本采样方式 subsample 和 colsample_bytree,MSE:0.297-->0.296。
step5:减小学习率并增大树个数
params = {
'seed': 0,
# 'eta': 0.1,
'colsample_bytree': 0.6,
'silent': 1,
'subsample': 0.7,
'objective': 'reg:squarederror',
'max_depth': 8,
'min_child_weight': 3,
'num_boost_round': 100,
'gamma': 0.1
}
cv_params = {'eta': [0.5, 0.4, 0.3, 0.2, 0.1, 0.075, 0.05, 0.04, 0.03]}
model = xgb.XGBRegressor(**params)
grid = GridSearchCV(estimator=model, param_grid=cv_params, scoring=mae_scorer, cv=5, verbose=1, n_jobs=4)
grid.fit(x_train, y_train)
test_predict = grid.predict(x_test)
mse = mean_squared_error(y_test, test_predict)
test_y = grid.predict(test_x)
print(grid.best_params_)
print(mse)
print(grid.best_score_)减小学习率并增大树个数,由于eta没变,MSE:不变。
六、总结
通过GridSerchCV调节参数,找打了一组最优参数,并切该参数下的模型结果最优,MSE最低,从调优前0.321的降到0.296。
最优参数:
best_params = {'max_depth' : 8,
'min_child_weight' : 3,
'gamma' : 0.1,
'colsample'_bytree : 0.6,
'subsample' : 0.7}