代码随想录算法训练营第18天 | 513.找树左下角的值、112. 路径总和 、113.路径总和ii、106.从中序与后序遍历序列构造二叉树、105.从前序与中序遍历序列构造二叉树
513.找树左下角的值
题目链接:找树左下角的值
解法:
这道题我的理解有误。最后一行最左边的值,不是说这个节点必须是最后一行的左叶子节点。如果最后一行,只有一个右叶子节点,那么因为只有一个,那么它就是最左边的。如果最后一行有多个叶子节点,那么不管它们是左节点还是右节点,总之是最左边的那个节点。
递归法:递归法有点难理解。使用前序遍历,深度最大的就是最后一行。记录深度最大的叶子节点,此时就是树的最后一行最左边的值。这里还要用到回溯,确实麻烦。如果保证取到最左边呢?因为记录了最大深度,如果是同一行的右边,那么深度一致,就不更新值了。
迭代法:迭代法非常简单,只需要记录最后一行第一个节点的数值就可以了。
边界条件:无
时间复杂度:
迭代法:O(n)
空间复杂度:
迭代法:O(n)
# 递归法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def findBottomLeftValue(self, root):
"""
:type root: TreeNode
:rtype: int
"""
self.max_depth = float("-inf")
self.result = None
self.traversal(root, 0)
return self.result
def traversal(self, root, depth):
if root.left is None and root.right is None:
if depth > self.max_depth:
self.max_depth = depth
self.result = root.val
return
if root.left:
depth += 1
self.traversal(root.left, depth)
depth -= 1
if root.right:
depth += 1
self.traversal(root.right, depth)
depth -= 1 # 迭代法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import deque
class Solution(object):
def findBottomLeftValue(self, root):
"""
:type root: TreeNode
:rtype: int
"""
queue = collections.deque([root])
result = None
while queue:
for i in range(len(queue)):
node = queue.popleft()
# 只需要记录最后一行第一个节点的数值就可以了
if i == 0:
result = node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result112. 路径总和
题目链接:112. 路径总和
解法:
递归法:不要去累加然后判断是否等于目标和,那么代码比较麻烦,可以用递减,让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
如果最后count == 0,同时到了叶子节点的话,说明找到了目标和。如果遍历到了叶子节点,count不为0,就是没找到。
需要用到回溯。
递归法可以写得比较简单,但是复杂的写法更直观。
迭代法:迭代法得用栈,属于前序遍历。关键在于,需要用两个栈,路径和不能用单一的变量来记录,而是需要记录每条路径的和。因为这里没有回溯,如果一条路径不对,换另外一条,那么单一变量是没法回溯的。
边界条件:为空
时间复杂度:
空间复杂度:
# 递归法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def hasPathSum(self, root, targetSum):
"""
:type root: TreeNode
:type targetSum: int
:rtype: bool
"""
if not root:
return False
# 通过减,而不是加,会更简单。记得进行初始化,减去root的值
return self.traversal(root, targetSum - root.val)
def traversal(self, root, count):
if root.left is None and root.right is None:
# 叶子节点且路径和等于target,则返回True
if count == 0:
return True
else:
return False
if root.left:
count -= root.left.val
# 只有为True才返回,会一直返回到根节点
if self.traversal(root.left, count):
return True
count += root.left.val
if root.right:
count -= root.right.val
if self.traversal(root.right, count):
return True
count += root.right.val
# 这里还有返回值
return False# 递归法,精简的写法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def hasPathSum(self, root, targetSum):
"""
:type root: TreeNode
:type targetSum: int
:rtype: bool
"""
if not root:
return False
# 通过减法,如果遇到叶子节点,且数值等于减去后剩下的数值,则存在
if root.left is None and root.right is None and root.val == targetSum:
return True
return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val) # 迭代法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def hasPathSum(self, root, targetSum):
"""
:type root: TreeNode
:type targetSum: int
:rtype: bool
"""
if not root:
return False
# 这里记录路径和也得用栈,不能用单一的值,不然减了或加了以后,
# 如果路径不对,还得回溯,而迭代法没有回溯的操作
stack = [(root, root.val)]
while stack:
node, path_sum = stack.pop()
if not node.left and not node.right and path_sum == targetSum:
return True
if node.right:
stack.append((node.right, path_sum + node.right.val))
if node.left:
stack.append((node.left, path_sum + node.left.val))
return False113.路径总和ii
题目链接:路径总和ii
解法:
递归法:这个题有了上一题的基础,思路差不多。但这个题的递归函数没有返回值,而是用一个全局变量results来记录所有满足条件的路径。最关键的一点是,某条路径,如果满足条件了,要进行深拷贝再加入到results中,不然回溯的时候会被改变,导致results中的结果也会改变。
迭代法:用深度优先遍历,前序遍历,栈。同样,需要两个栈。而且需要注意在更新左子树和右子树的路径时,path本身要不变,不然相当于左子树的路径和右子树的路径加在一块了,因此不要用append的操作。
边界条件:
时间复杂度:
空间复杂度:
# 递归法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def pathSum(self, root, targetSum):
"""
:type root: TreeNode
:type targetSum: int
:rtype: List[List[int]]
"""
if not root:
return []
self.targetSum = targetSum
self.results = []
self.traversal(root, [root.val])
return self.results
def traversal(self, root, path):
if not root.left and not root.right and sum(path) == self.targetSum:
# 这里得注意,必须拷贝,不然后面回溯,会改变已经加入结果的路径!!!
self.results.append(path[:])
if root.left:
path.append(root.left.val)
self.traversal(root.left, path)
path.pop()
if root.right:
path.append(root.right.val)
self.traversal(root.right, path)
path.pop()# 迭代法
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def pathSum(self, root, targetSum):
"""
:type root: TreeNode
:type targetSum: int
:rtype: List[List[int]]
"""
if not root:
return []
results = []
stack = [(root, [root.val])]
while stack:
node, path = stack.pop()
if not node.left and not node.right and sum(path) == targetSum:
results.append(path)
if node.right:
# 注意新的path用这个写法,那么原path不变,
# 可用于更新左节点的path,而且写法简洁
stack.append((node.right, path + [node.right.val]))
if node.left:
stack.append((node.left, path + [node.left.val]))
return results106.从中序与后序遍历序列构造二叉树
题目链接:中序和后序遍历重构二叉树
解法:
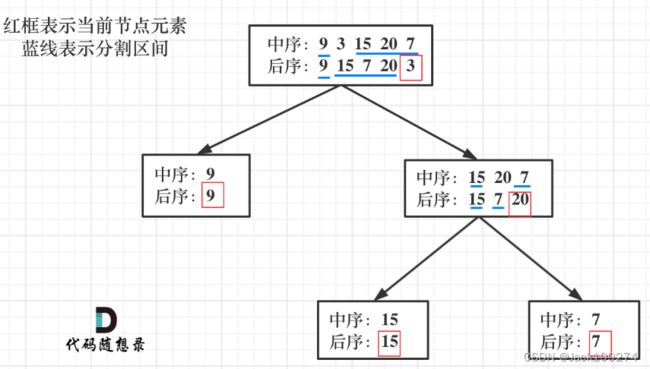
以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
边界条件:无
时间复杂度:
空间复杂度:
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def buildTree(self, inorder, postorder):
"""
:type inorder: List[int]
:type postorder: List[int]
:rtype: TreeNode
"""
# 第一步:树为空,则递归终止
if not inorder or not postorder:
return None
# 第二步:从后序遍历,得到中间节点
mid_val = postorder[-1]
mid_node = TreeNode(val=mid_val)
# 第三步:找到切割点
mid_idx = inorder.index(mid_val)
# 第四步:切割inorder数组
left_inorder = inorder[:mid_idx]
right_inorder = inorder[mid_idx+1:]
# 第五步:切割postorder数组,左右都和inorder一样长
left_postorder = postorder[: mid_idx]
right_postorder = postorder[mid_idx:-1]
# 第六步:递归,重构左子树和右子树
mid_node.left = self.buildTree(left_inorder, left_postorder)
mid_node.right = self.buildTree(right_inorder, right_postorder)
return mid_node105.从前序与中序遍历序列构造二叉树
题目链接:前序和中序遍历重构二叉树
解法:
注意递归传入参数的顺序是 先preorder,再inorder,由于先分割inorder,所以容易把inorder作为第一个参数传入。这种错误是非常难发现的!
再就是获取中间节点的值,是preorder的第0个元素,而不是最后一个。
总之,这两点容易和上一题混淆。
边界条件:
时间复杂度:
空间复杂度:
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
if not inorder:
return None
mid_val = preorder[0]
mid_node = TreeNode(mid_val)
mid_idx = inorder.index(mid_val)
left_inorder = inorder[:mid_idx]
right_inorder = inorder[mid_idx+1:]
left_preorder = preorder[1: mid_idx+1]
right_preorder = preorder[mid_idx+1:]
mid_node.left = self.buildTree(left_preorder, left_inorder)
mid_node.right = self.buildTree(right_preorder, right_inorder)
return mid_node