正则表达式转NFA，DFA,最小化DFA

Exp 2：正则表达式转NFA，DFA,最小化DFA

（1）正则表达式应该支持单个字符，运算符号有： 连接 选择(|) 闭包(*) 正闭包（+） 可选（?） 括号
（2）要提供一个源程序编辑界面，让用户输入表示生成流水线处理过程的正则表达式（可保存、打开正则表达式文件）
（3）需要提供窗口以便用户可以查看转换得到的NFA（用状态转换表呈现即可）
（4）需要提供窗口以便用户可以查看转换得到的DFA（用状态转换表呈现即可）
（5）需要提供窗口以便用户可以查看转换得到的最小化DFA（用状态转换表呈现即可）

本实验的设计还是有点不够简洁。大家如果有能力还是自己再优化设计一下。 里面还是存在一些鸡肋的设计。

结构的设计

1. 基本节点

有状态，字符（用来记录‘^’,'# ',其他字符这些），指向下一个节点的指针。用来表示一个圆圈以及一个箭头。

struct Linknode
{
    int stateNum = -1;
    QChar worker = '#';
    Linknode* next = nullptr;
    Linknode(int s, QChar c, Linknode* n=nullptr)
    {
        stateNum = s;
        worker = c;
        next = n;
    }
};

2.NFA的基本节点，用来传递参数。(函数需要接受初态和终态)

struct NFA{
    Linknode* start = nullptr;
    Linknode* end = nullptr;
    NFA(Linknode* s, Linknode* e){
        start = s;
        end = e;}
};

3.DFA基本节点

因为DFA一个节点要存放一个字符集合，所以使用 QSet结构

struct dfaNode{
    QSet<int> statu_set;
    QChar worker = '#';
    dfaNode* next = nullptr;
};

4.minDFA

struct minDfaNode{
    int state_num;
    QChar worker = '#';
    bool finish = false;
    minDfaNode* next = nullptr;
};

5.窗口的统一结构

class Linklist{
public:
    Linklist();
    QVector<Linknode*> vertexs; //NFA邻接表的表头
    QVector<dfaNode*> dfalist;  //DFA邻接表的表头
    QVector<minDfaNode*> mindfalist;  //最小化邻接表的表头
    Linknode* first; 
    dfaNode* dfa_first;    
    minDfaNode* mindfa_first;
}

6.实际在QT窗口使用的结构是；

class MainWindow : public QMainWindow{
    Q_OBJECT
public:
    QString raw_r; //输入的正则表达式
    QString process_r;  //后缀表达式
    Linklist* link_table = new Linklist();  //总的头
    int state_num = 0;
    QString xlex;
    QString save_path;
    QStack<NFA*> nfa_stack;
    QVector<QChar> alphabet;
    QString Process(QString raw);
}

1.输入正则表达式

第一步：特殊运算符： ‘&’ ， ‘|’ ， ‘*’ ， ‘+’ ， ‘?’ , ‘[ ]’

扫描一行符号

1.去掉空格
2.方括号要转换形式，从[1-5],变成 （1|2|3|4|5）这样方便进一步转换

因为连接符号在正则表达式中是隐形的，所以为了转换，需要手动加上‘&’表示连接符号。

1. 两个字符之间需要加一个 “&”
   这几种情况要加& ： “a a” 、“a (” 、“* a” 、“* (” 、“) a” 、 “) (”
   比如原字符串：a|bcs[1-3]asds
   加&后 ： a|b&c&s&(1|2|3)&a&s&d&s
   开始遍历
   如果栈内的运算符优先级大于等于当前运算符，则弹出栈内运算符

 //添加连接符'&'
    int length = raw.length();
    QString rawadd;
    for(int i=0;i<length;i++)
    {
        rawadd.append(raw[i]);
        if(i < length-1 && ((isAlpha(raw[i]) && isAlpha(raw[i+1])) || (isAlpha(raw[i]) && raw[i+1] == '(') || (raw[i] == '*' && isAlpha(raw[i+1]))
                            || (raw[i] == '*' && raw[i+1] == '(') || (raw[i] == ')' && isAlpha(raw[i+1])) || (raw[i] == ')' && raw[i+1] == '(')))
        {
            rawadd.append('&');
        }
    }

字符可以直接加入到 总的字符串中，因为在中缀和后缀表达式中，数字的位置都是一样的。遇到5大符号（ ‘&’ ， ‘|’ ， ‘*’ ， ‘+’ ， ‘?’），则需要单独处理，进入栈中，这块还有一些逻辑。

‘[ ]’

方括号太抽象， 这里转换成更具体的范围 （||||） 用圆括号和 || 来表示
QString::toLatin1是相当于 ASCii码不包含中文的遇到中文默认转换为ascii码。
bracket（）函数 ， 即当遇到[ - ]这段的时候，用 （||||）替代，其他原封不动的保存。

QString bracket(QString raw)
{
    QString p;
    int i=0;
    while(i<raw.length())
    {
        if(raw[i] == '[')
        {
            p.append('(');
            char c1 = raw[++i].toLatin1();
            p.append(c1);
            i++;
            char c3 = raw[++i].toLatin1();
            for(int j=(c1-'0')+1;j<=(c3-'0');j++)
            {
                p.append('|');
                p.append(char(j+'0'));
            }
            i++;
            p.append(')');
        }else
        {
            p.append(raw[i]);
        }
        i++;
    }
    return p;
}

正则表达式是中缀的，但是为了方便使用后缀表达式 （其实也可以不转换，直接用双栈结构来完成，一个符号栈，一个字母栈。但是没有这么做。）

中缀表达式 9+（3-1）x3+10÷2
后缀表达式9 3 1 - 3 x + 10 2 ÷ +
开两个栈结构，一个放数字，一个放符号。
从左到右。9 入数字栈
+号 入符号栈（目前栈空，栈空就进栈）
（ 入符号栈
目前栈里从上到下：（ +
3入数字栈
当前表达式为 9 3

• 入栈
  目前栈里从上到下：-（ +
  正则表达式中总共有以下的符号。

算法思路如下：

QString process, 和一个栈结构 operator
process相当于数字栈， operator 相当于符号栈

 //转换成后缀表达式
    int i=0;
    length = rawadd.length();
    QString process;
    while(i < length)
    {
        if(isAlpha(rawadd[i]))//遇到字符直接输出
        {
            process.append(rawadd[i]);
        }
        else if(rawadd[i] == '(')
        {
            operate.push(rawadd[i]);
        }
        else if(rawadd[i] == ')')
        {
            //不断弹出操作符号知道遇到'('
            while(operate.top() != '(')
            {
                process.append(operate.pop());
            }
            operate.pop();
        }
        else if((rawadd[i] == '&') || (rawadd[i] == '|') || (rawadd[i] == '*') || rawadd[i] == '+' || rawadd[i] == '?')
        {
            if(!operate.empty())
            {
                QChar t = operate.top();
                if(Priority(t) >= Priority(rawadd[i]))//如果栈内的运算符优先级大于等于当前运算符，则弹出栈内运算符
                {
                    process.append(operate.pop());
                }
            }
            operate.push(rawadd[i]);//把当前运算符入栈
        }
        if(i == length-1)//读完字符串，把剩下的符号全部弹出
        {
            while(!operate.empty())
            {
                process.append(operate.pop());
            }
        }
        i++;
    }

NFA，就是基本结构，由两个点一条边构成。 相比于DFA，NFA就是多加空的边。这样方便合并，不会过于复杂。

正则表达式转成后缀之后，就可以开始构建图结构。
以邻接表形式存储NFA图
后缀表达式，按照扫描的方式来做：
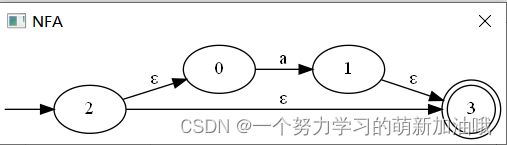
基本NFA图：
是两个结点一条边。

之后构图就是由这些基本结点连接，形成图。
而连接这些基本的结点的就是空，一条边。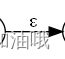

手工做NFA图，以及状态转换表

首先知道运算符号的优先级：
最高优先级： 闭包（ * ），正闭包（ + ），? （可选符号）
第二级：连接（ & ）
第三级： 选择（ | ）
第四级： 右括号（（ ）

一、 连接运算符： a&b

节点编号就是按顺序，这边编号可以忽略。

 else if(process_r[i] == '&'){
            NFA* s = nullptr;
            NFA* e = nullptr;
            if(!nfa_stack.empty())
            {
                e = nfa_stack.pop();
            }
            if(!nfa_stack.empty())
            {
                s = nfa_stack.pop();
            }
            NFA* new_n = link_table->addNFA(s, e);
            nfa_stack.push(new_n);
        }

NFA* Linklist::addNFA(NFA* s, NFA* e){
    //空串连接两个状态
    Linknode* a = new Linknode(e->start->stateNum, '^');
    vertexs[s->end->stateNum]->next = a;
    e->start->worker = '^';
    //压入新的NFA部分
    NFA* new_n = new NFA(s->start, e->end);
    return new_n;
}

在邻接表中，需要新的节点来连接，所以新创建了一个节点。

二、选择运算符号 ： a|b

or （a|b)

转成后缀之后，变成了 ===== > ab|
所以先生成两个基本NFA结构。
然后扫描到选择符号。设计一个函数来完成。
函数参数是两个NFA图，包括每一个的初态和终态。用于连接操作。
返回值： 一个合并后的NFA图

选择符号需要加两个节点，一个初态节点，一个终态节点。

初态节点要加两条边连接两个NFA图的初态。
两个NFA图的终态要各出一条边连接到新终态节点。
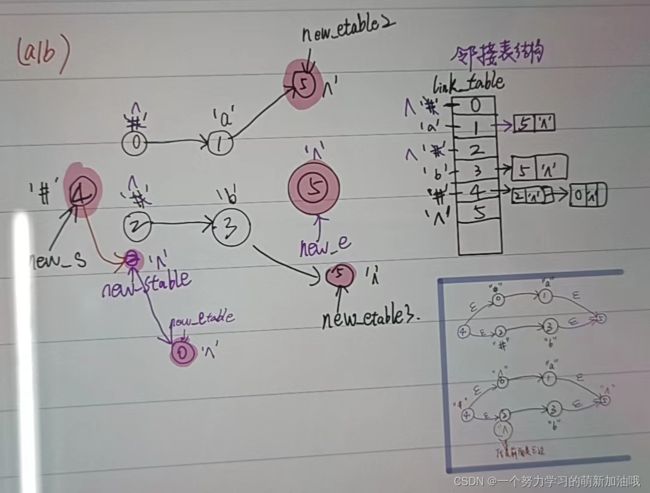
便于理解的图。

实际构建的图如下：
下图中紫色的就是需要添加的部分
加工后：加“^”,也是为了后面代码画图的时候，分辨出来是伊普西隆。


选择运算也是一样，需要把所有的初态和终态都新建立，连接到邻接表中。

NFA* Linklist::orNFA(int& snum, NFA *s, NFA *e){
    //新的初态
    Linknode* new_s = new Linknode(snum++, '#');
    vertexs.append(new_s);//加入邻接表数组
    //新初态连接两部分
    s->start->worker = '^';
    e->start->worker = '^';
    Linknode* new_etable = new Linknode(e->start->stateNum, e->start->worker);
    Linknode* new_stable = new Linknode(s->start->stateNum, s->start->worker);
    new_stable->next = new_etable;
    new_s->next = new_stable;
    //新的终态
    Linknode* new_e = new Linknode(snum++, '^');
    vertexs.append(new_e);//加入邻接表数组
    //新终态连接两部分
    Linknode* new_etable2 = new Linknode(new_e->stateNum, new_e->worker);
    vertexs[s->end->stateNum]->next = new_etable2;
    Linknode* new_etable3 = new Linknode(new_e->stateNum, new_e->worker);
    vertexs[e->end->stateNum]->next = new_etable3;
    //压入新的NFA部分
    NFA* new_n = new NFA(new_s, new_e);
    return new_n;
}

三、闭包运算符号 ： a*

a的0-n个连接。

![在这里插入图片描述](https://img-blog.csdnimg.cn/7166b9817eee474896161adf9d8c258f.png

NFA* Linklist::closureNFA(int& snum, NFA* s)
{
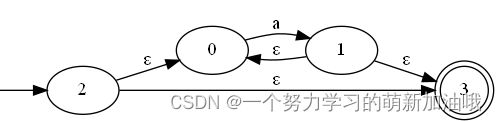
    //新的初态并连接
    Linknode* new_s = new Linknode(snum++, '#');
    s->start->worker = '^';
    Linknode* new_stable = new Linknode(s->start->stateNum, s->start->worker);
    new_s->next = new_stable;
    vertexs.append(new_s);//加入邻接表数组

    //新的终态并连接
    Linknode* new_e = new Linknode(snum++, '^');
    vertexs.append(new_e);//加入邻接表数组

    Linknode* new_etable = new Linknode(new_e->stateNum, '^');
    Linknode* new_etable2 = new Linknode(new_e->stateNum, '^');
    vertexs[s->end->stateNum]->next = new_etable;//旧终态连接
    new_stable->next = new_etable2;//新初态连接

    //旧初态和旧终态的连接
    Linknode* new_stable2 = new Linknode(s->start->stateNum, s->start->worker);
    new_etable->next = new_stable2;

    //压入新的NFA部分
    NFA* new_n = new NFA(new_s, new_e);
    return new_n;
}

四、圆括号 ： （ 1- 10）

圆括号的作用就是，把一堆东西当作一个整体。后缀表达式中不包括括号，

例子：

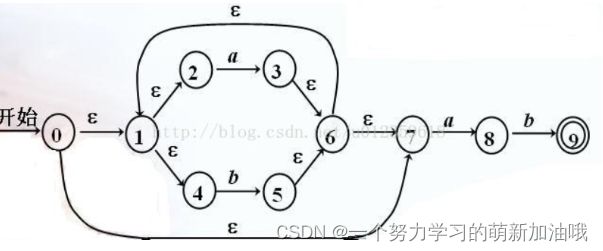
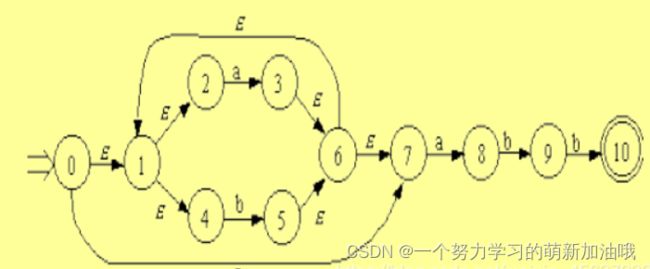
源字符串： a|b*[1-3]a*
加了&之后：a|b*&(1|2|3)&a*
变成后缀之后：ab12|3|&a&|
现在用后缀生成NFA状态表和图结构

这里定义一个NFA类，NFA有两个指针，分别指向初态和终态。

只做记录，不做连接。 其实是为了函数传参。做连接的还是Linktable,其中是带有指针的节点作为组成部分。这里用Linktable 来完成。具体结构如下：

NFA只是为了传递参数。 重要的还是 Linklist* link_table = new Linklist();

class Linklist
{
public:
    Linklist();
    QVector<Linknode*> vertexs;
 }

五、问号 ： （？）

以 a?为例：

 else if(process_r[i] == '?')
        {
            NFA* s = nullptr;
            if(!nfa_stack.empty())
            {
                s = nfa_stack.pop();
            }
            NFA* new_n = link_table->seleNFA(state_num, s);
            nfa_stack.push(new_n);
        }

NFA* Linklist::seleNFA(int &snum, NFA *s)
{
    //新的初态并连接
    Linknode* new_s = new Linknode(snum++, '#');
    s->start->worker = '^';
    Linknode* new_stable = new Linknode(s->start->stateNum, s->start->worker);
    new_s->next = new_stable;
    vertexs.append(new_s);//加入邻接表数组
    //新的终态并连接
    Linknode* new_e = new Linknode(snum++, '^');
    vertexs.append(new_e);//加入邻接表数组
    
    Linknode* new_etable = new Linknode(new_e->stateNum, '^');
    Linknode* new_etable2 = new Linknode(new_e->stateNum, '^');
    vertexs[s->end->stateNum]->next = new_etable;//旧终态连接
    new_stable->next = new_etable2;//新初态连接
    
    //压入新的NFA部分
    NFA* new_n = new NFA(new_s, new_e);
    return new_n;
}

六、正闭包，（+）

 else if(process_r[i] == '+')
        {
            NFA* s = nullptr;
            if(!nfa_stack.empty())
            {
                s = nfa_stack.pop();
            }
            NFA* new_n = link_table->opClosureNFA(state_num, s);
            nfa_stack.push(new_n);
        }

NFA* Linklist::opClosureNFA(int& snum, NFA* s)
{
    //新的初态并连接
    Linknode* new_s = new Linknode(snum++, '#');
    s->start->worker = '^';
    Linknode* new_stable = new Linknode(s->start->stateNum, s->start->worker);
    new_s->next = new_stable;
    vertexs.append(new_s);//加入邻接表数组

    //新的终态并连接
    Linknode* new_e = new Linknode(snum++, '^');
    vertexs.append(new_e);//加入邻接表数组

    Linknode* new_etable = new Linknode(new_e->stateNum, '^');
    vertexs[s->end->stateNum]->next = new_etable;//旧终态连接

    //旧初态和旧终态的连接
    Linknode* new_stable2 = new Linknode(s->start->stateNum, s->start->worker);
    new_etable->next = new_stable2;

    //压入新的NFA部分
    NFA* new_n = new NFA(new_s, new_e);
    return new_n;
}

邻接表中的邻接点都是新建立的。 在vector 数组中不能进行连接，所以代码会比较复杂。

所有的连接都是创建新的节点，和新的节点连接。
下面的代码中， new_stable ,new_stable2, new_etable, new_etable2都是在链表后面加邻接点。
例: vertexs[s->end->stateNum]->next = new_etable2;

正则表达式-》NFA完成啦（以上的方法有个名字： Thompson方法）

下一步：NFA->DFA

思路就是： 1. epsilon 转换。2.多重转换（去掉一对多）

1. epsilon 转换

epsilon连接的两个点可以理解为等价的状态。
** 手工做法：穷举所有可能的情况**

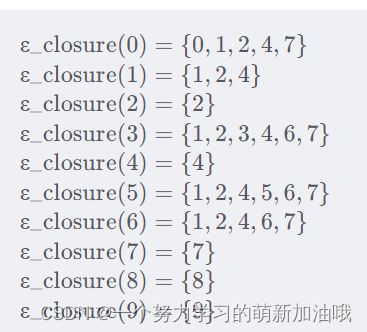
由节点1作为起点，
看有几个字母，状态转换表就有几列。
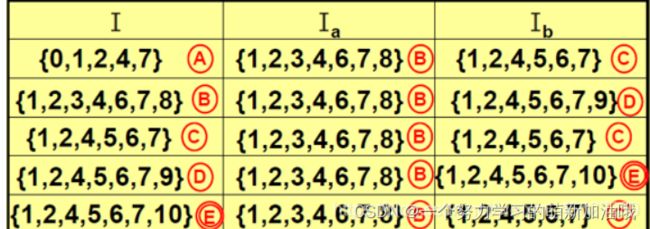
步骤2中有A,B,C,D四种情况，其中A是初始情况（ε _ c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } ε_closure(0)={0,1,2,4,7}ε_closure(0)={0,1,2,4,7}. 多说几句，在NFA图1中，是从0出发的，所以初始情况是ε _ c l o s u r e ( 0 ) ε_closure(0)ε_closure(0)，那假设如果是从X开始，则初始情况是ε _ c l o s u r e ( X ) ε_closure(X)ε_closure(X)）



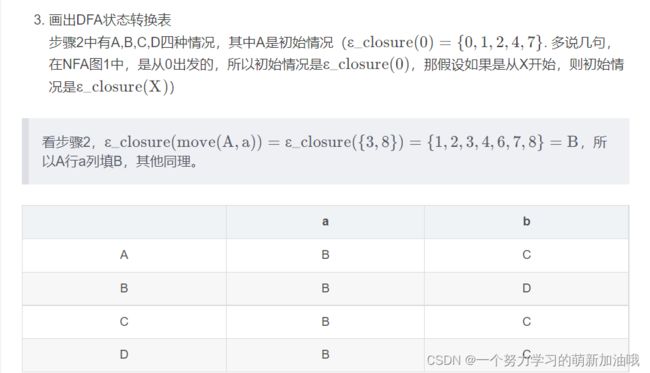
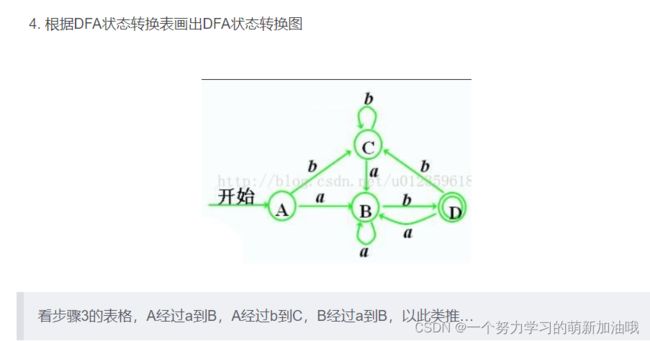
手工做法结束。代码思路如下：

思路

DFA也是一个图。使用dfa_first表示。
DFA图，用一个新的结构体表示。
因为有可能存在等价状态。所以用一个集合表示。

struct dfaNode{
    QSet<int> statu_set;
    QChar worker = '#';
    dfaNode* next = nullptr;
};

可以看的状态转换表格，状态部分，由1-n个节点等价。

第一步：完成找到和本节点以epsilon连接的点的一个集合。

每次都是从状态0 开始。

初始化 DFA

void MainWindow::iniDFAFirst()
{
    link_table->first = nfa_stack.top()->start;                                  //获取初态
    link_table->dfa_first = new dfaNode();
    link_table->dfsEpsilon(link_table->first, link_table->dfa_first->statu_set);//寻找初态的等价状态
    link_table->dfalist.push_back(link_table->dfa_first);
}

注意：

这里的dfa 先使用初态为链表头。 进行初始化。
比如 a*
获得的第一个状态是2, 并且和0，3都是epsilon连接的。所以第一个DFA结点 中字符集合是{2，0，3}

本步骤：找到与0 等价的所有结点，并且把该状态加入到集合中。

void Linklist::dfsEpsilon(Linknode* p, QSet<int>& f){
    while(p != nullptr)
    {
        if(p->worker == '^' || p->worker == '#')
        {
            f.insert(p->stateNum);
            if(p->next != nullptr)
                dfsEpsilon(vertexs[p->next->stateNum], f);
       }
        else {
            return; }
        p = p->next;
   }
 }

经过字符 QChar c之后到达的状态加入到集合s 中

void Linklist::dfsChar(dfaNode* p, QChar c, QSet<int>& s)
{
    QVector<int> t;
    QSet<int>::iterator iter;
    for(iter = p->statu_set.begin(); iter != p->statu_set.end(); iter++)
    {
        if(s.contains(vertexs[*iter]->stateNum)) {//不重复添加
            continue;
        }
        Linknode* a = vertexs[*iter]->next;//查找在该状态中的所有结点的邻接点
        while(a != nullptr)
        {
            if(a->worker == c && !vectorfind2(t, vertexs[*iter]->stateNum))//如果是通过一个字符c到达的结点则放入t
            {
                t.push_back(a->stateNum);
                if(vertexs[a->stateNum]->next!=nullptr) dfsEpsilon(vertexs[vertexs[a->stateNum]->next->stateNum], s);
            }
            a = a->next;
        }
    }
    //已有的集合经过一个字符c能到达的点也需要加入集合
    QSet<int>::iterator iter1;
    for(iter1 = s.begin(); iter1 != s.end(); iter1++)
    {
        Linknode* a = vertexs[*iter1]->next;
        while(a != nullptr)
        {
            if(a->worker == c)
            {
                s.insert(a->stateNum);
            }
            a = a->next;
        }
    }

    for(int i=0;i<t.size();i++)//遍历所有a状态能通过字符c到达的结点
    {
        Linknode* a = vertexs[t[i]]->next;//遍历这些结点的邻接点
        while(a != nullptr)
        {
            if(a->stateNum == 11) qDebug()<<"11";
            dfsEpsilon(vertexs[a->stateNum], s);//把通过一个字符c能到达的结点的能通过epsilon到达的结点加入集合s
            a = a->next;
        }
    }
    VectorToSet(t, s);//把经过一次字符c的结点中被选择的放入
}

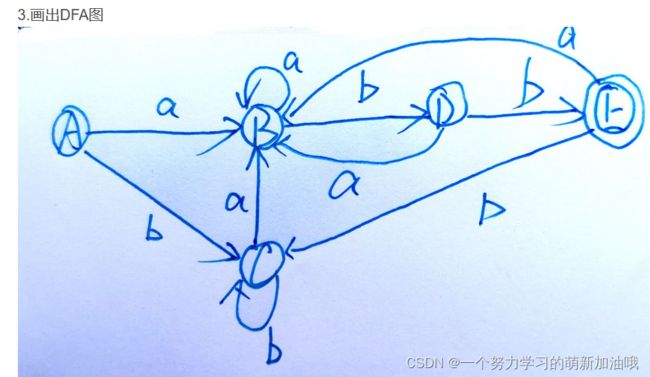
转换成DFA的部分

void MainWindow::iniDFAFirst()
{
    link_table->first = nfa_stack.top()->start;                                 //获取初态
    link_table->dfa_first = new dfaNode();
    link_table->dfsEpsilon(link_table->first, link_table->dfa_first->statu_set);//寻找初态的等价状态
    link_table->dfalist.push_back(link_table->dfa_first);
}

void MainWindow::toDFA()
{
    iniDFAFirst(); //初始化表头结点
    for(int j=0;j<link_table->dfalist.size();j++)
    {
        for(int i = 0;i<alphabet.size();i++)
        {
            dfaNode* d = new dfaNode();
            link_table->dfsChar(link_table->dfalist[j], alphabet[i], d->statu_set);

            if(d->statu_set.size() != 0)
            {
                d->worker = alphabet[i]; //经过的字符 alphabet[i]
                d->next = link_table->dfalist[j]->next;
                link_table->dfalist[j]->next = d;
            }
            else
            {
                delete  d;
                continue;
            }
            dfaNode* new_d = new dfaNode();
            new_d->statu_set = d->statu_set; //复制一份 d 的信息，不能直接连接到邻接表中
            new_d->worker = d->worker;

            if(new_d->statu_set.size() != 0  && link_table->dfalist[j]->statu_set != new_d->statu_set && !Vectorfind(link_table->dfalist, new_d))
                link_table->dfalist.push_back(new_d);
        }
    }
}

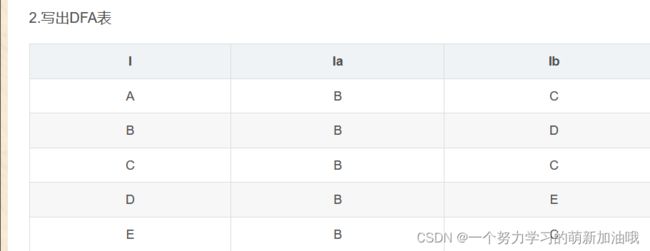
转成表格

void MainWindow::DFAtoForm()
{
    QStandardItemModel * model = new QStandardItemModel();
    //设置列
    model->setColumnCount(alphabet.size()+1); //设置列数
    model->setHorizontalHeaderItem(0, new QStandardItem("状态"));
    for(int i=1;i<=alphabet.size();i++)
    {
        model->setHorizontalHeaderItem(i, new QStandardItem(QString(alphabet[i-1])));
        for(int j=0;j<link_table->dfalist.size();j++)
        {
            dfaNode* p = link_table->dfalist[j]->next;
            QString state_set = "";
            while(p != nullptr)
            {
                if(p->worker == alphabet[i-1])
                {
                    QSet<int>::iterator iter1;
                    for(iter1 = p->statu_set.begin(); iter1 != p->statu_set.end(); iter1++)
                    {
                        state_set.append("  " + QString::number(*iter1)  + ",");
                    }
                }
                p = p->next;
            }
            model->setItem(j, i, new QStandardItem(state_set));
        }
    }
    //设置状态列
    for(int i=0;i<link_table->dfalist.size();i++)
    {
        dfaNode* p = link_table->dfalist[i];
        QString state_set = "";
        QSet<int>::iterator iter1;
        for(iter1 = p->statu_set.begin(); iter1 != p->statu_set.end(); iter1++)
        {
            state_set.append("  " + QString::number(*iter1)  + ",");
        }
        model->setItem(i, 0, new QStandardItem(state_set));//第一列的设置。把所有状态列出。
    }
    ui->tableView_4->setModel(model);
}

下面介绍DFA最小化
借用一个博主的
解题过程如下：

1.根据状态转换图写出状态转换表

算法思路

1.先把所有状态放入一个vector, 通过查找dfaNode的集合是否相同来获取对应的下标作为新的状态号

QVector<dfaNode*> v;
    for(int i=0;i<dfalist.size();i++)
    {
        dfaNode* d = new dfaNode();
        d->statu_set = dfalist[i]->statu_set;
        v.push_back(d);
    }

2. 遍历邻接表, 替换所有的状态集合为新的状态号

for(int i=0;i<dfalist.size();i++)
    {
        //形成mindfa邻接表数组
        dfaNode* p = dfalist[i];
        minDfaNode* f = new minDfaNode();
        int index;
        if(vectorfind(v, p, index))//获取新的状态号
        {
            f->state_num = index;
            f->worker = p->worker;
  if(p->statu_set.contains(vertexs.size()-1)) f->finish = true;//标记是否是终态，用以划分
            mindfalist.push_back(f);
        }

        //形成mindfa邻接表的邻接点
        p = p->next;
        while(p != nullptr)
        {
            int index2;
            if(vectorfind(v, p, index2))//获取新的状态号
            {
                minDfaNode* k = new minDfaNode();
                k->state_num = index2;
                k->worker = p->worker;
                if(p->statu_set.contains(vertexs.size()-1)) k->finish = true;//标记是否是终态，用以划分
                k->next = f->next;
                f->next = k;
            }
            p = p->next;
        }
    }

找状态号的函数

bool vectorfind(QVector<dfaNode*> v, dfaNode* d, int& index)
{
    for(int i=0;i<v.size();i++){
        if(d->statu_set == v[i]->statu_set)
        {
            index = i;
            return true;
        }
    }
    index = -1;
    return false;
}