正则表达式和自动机(DFA&NFA)
文章目录
-
- 一 正则表达式匹配原理
-
- 1.1 正则表达式
- 1.2 DFA
- 1.3 正则表达式和DFA的关系
- 1.4 正则匹配过程
- 二 DFA的构建
- 三 DFA与正则的转化
-
- 3.1 DFA转正则表达式
- 3.2 正则表达式转DFA
-
- 3.2.1 正则表达式转NFA
- 3.2.2 NFA确定化
- 四 js中的正则
一 正则表达式匹配原理
1.1 正则表达式
正则表达式是对字符串操作的一种逻辑公式,就是用事先定义好的一些特定字符、及这些特定字符的组合,组成一个“规则字符串”,这个“规则字符串”用来表达对字符串的一种过滤逻辑。例如,筛选所有以包含连续三个0的0,1字符串的正则表达式为:
( 0 ∪ 1 ) ∗ 000 ( 0 ∪ 1 ) ∗ (0\cup 1)^*000(0\cup 1)^* (0∪1)∗000(0∪1)∗
1.2 DFA
DFA(Deterministic Finite State),确定有穷自动机,从一个状态通过一系列的事件转换到另一个状态。它的形式定义如下:
有穷自动机是一个5元组 ( Q , E , δ , q 0 , F ) (Q,E, \delta ,q_0,F) (Q,E,δ,q0,F),其中:
- Q Q Q是一个有穷集合,叫做状态集。
- E E E是一个有穷集合,叫做字母集。
- δ \delta δ:$Q\times \Sigma \rightarrow Q $是转移函数。
- q 0 ∈ Q q_0 \in Q q0∈Q是起始状态。
- F ⊆ Q F \subseteq Q F⊆Q是接受状态集。
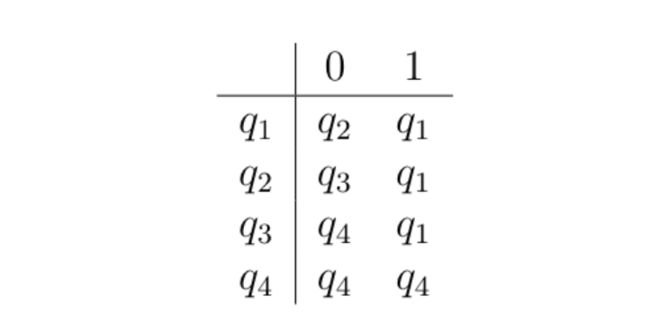
举个例子,有一个有穷自动机 G = ( Q , E , δ , q 0 , F ) G=(Q,E, \delta ,q_0,F) G=(Q,E,δ,q0,F),其中:
Q = { q 1 , q 2 , q 3 , q 4 } Q = \{q_1,q_2,q_3,q_4\} Q={q1,q2,q3,q4}。 表示该自动机共有4个状态
E = { 0 , 1 } E=\{0,1\} E={0,1};表示该自动机只接收0,1字母
q 0 = q 1 q_0=q_1 q0=q1;表示开始状态为 q 1 q_1 q1
F = { q 4 } F=\{q_4\} F={q4}。表示结束状态有 q 4 q_4 q4;
我们可以根据该自动机画出下面这一个图,来形象的理解一下。
1.3 正则表达式和DFA的关系
正则表达式就是建立在自动机的理论基础上的:用户写完正则表达式之后,正则引擎会按照这个表达式构建相应的自动机,也就是说,一个正则表达式必定可以构建出与之对应的DFA,正则表达式与DFA之间的比例关系为1:n。
1.4 正则匹配过程
现在有字符串 S 1 = 1010001 S1 = 1010001 S1=1010001,计算机在判断它是否匹配正则表达式 ( 0 ∪ 1 ) ∗ 000 ( 0 ∪ 1 ) ∗ (0\cup 1)^*000(0\cup 1)^* (0∪1)∗000(0∪1)∗时,匹配的步骤如下:
| 开始状态 | 到达状态 | 输入字符 | 剩余字符串 | 是否接受 |
|---|---|---|---|---|
| q 1 q_1 q1 | q 1 q_1 q1 | 1 | 010001 | 否 |
| q 1 q_1 q1 | q 2 q_2 q2 | 0 | 10001 | 否 |
| q 2 q_2 q2 | q 1 q_1 q1 | 1 | 0001 | 否 |
| q 1 q_1 q1 | q 2 q_2 q2 | 0 | 001 | 否 |
| q 2 q_2 q2 | q 3 q_3 q3 | 0 | 01 | 否 |
| q 3 q_3 q3 | q 4 q_4 q4 | 0 | 1 | 否 |
| q 4 q_4 q4 | q 4 q_4 q4 | 1 | ε \varepsilon ε | 是 |
判定一个字符串匹配某个正则表达式,即当所有字符串输入到自动机中,最终停留的状态为接受状态。
二 DFA的构建
例如,我们现在需要构建一个识别手机号码的自动机,我们需要先明白手机号码所有的限制规则,为了方便画图,我们这里假定所有的手机号码都是5位,那么所有的规则为:
- 5位,第一位一定是1。
- 第二位和第三位根据不同运营商的号码段有所区别,只有有限的组合是合法的手机号码。
- 手机号码第二位为3,第三位可以是任意数字。
- 手机号码第二位为5,第三位为0-3或7-9任意一个数字。
- 后2位可以是任意数字。
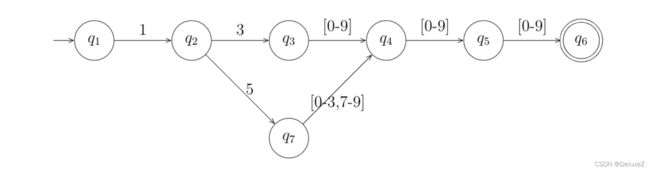
根据规则构建一个自动机的步骤如下:
当然,构造DFA还有很多技巧,例如联结和取非等。
三 DFA与正则的转化
3.1 DFA转正则表达式
从一个DFA转化为一个正则表达式,我们需要知道下面三条构造规则:

除此之外,我们还需要知道,在转化为正则表达式时,我们只关心由开始到接受状态的所有路径。所以在自动机的图里面,除了自我闭环的路径,只有指向自己而没有指出的状态是无用状态,例如上面电话号码的例子中, q 8 q_8 q8状态实际上是一个没用的状态。
根据以上三条规则的第一条,我们可以得到下面的自动机:

根据第二条规则,我们可以得到下面的自动机:

再根据第一条规则,我们可以得到下面的自动机:

所以,电话号码的正则表达式为: 1 ( 3 [ 0 − 9 ] ∣ 5 [ 0 − 3 , 7 − 9 ] ) [ 0 − 9 ] [ 0 − 9 ] 1(3[0-9]\mid 5[0-3,7-9])[0-9][0-9] 1(3[0−9]∣5[0−3,7−9])[0−9][0−9]。
当然,在转化过程中,最终的接受状态可能会有很多个,例如:
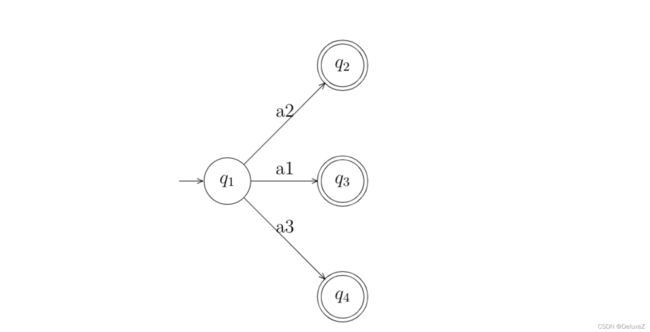
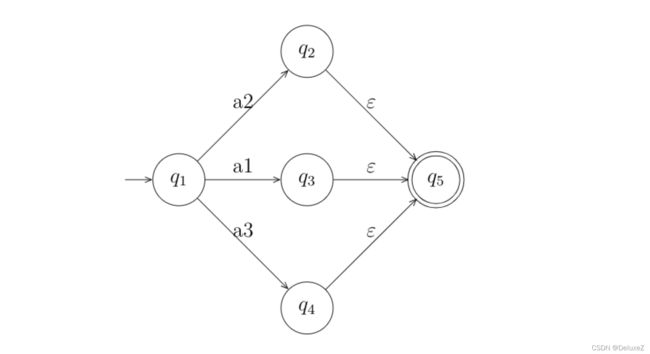
我们可以通过将这些终止节点都连接到一个同一个虚拟的终止节点,在进行状态合并。
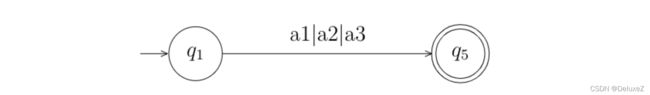
3.2 正则表达式转DFA
正则表达式转DFA需要分为两步,首先,需要将正则表达式转化为NFA,再将NFA确定化。
NFA(Nondeterministic Finite Automaton),非确定有限状态自动机。它与DFA的区别是,一个状态接收某个字符串的下一个状态是不确定的,以及在状态转化中可以接收空字符串 ε \varepsilon ε。
3.2.1 正则表达式转NFA
从一个DFA转化为一个正则表达式,我们需要知道下面三条构造规则:
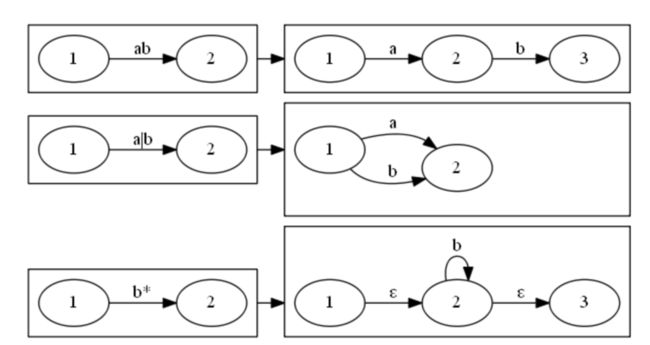
需要注意的是第三条规则有两个空串,我们可能会想能不能省略掉最后那个空边呢?答案是不行的,因为在某些情况下可能会有错误。
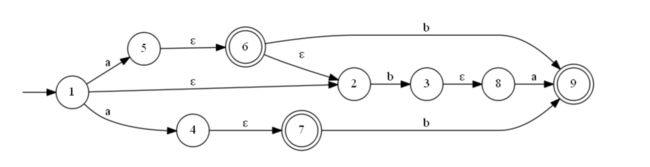
举个例子:正则表达式 ( a ∣ b ) ( c ∣ d ) ∗ ( e ∣ f ) (a\mid b)(c\mid d)^*(e\mid f) (a∣b)(c∣d)∗(e∣f)。将这个正则表达式转化为NFA。
根据第一条规则,我们可以得到如下的NFA:

根据第二、三条规则我们可以得到如下NFA:

3.2.2 NFA确定化
NFA的确定化:由NFA构造出与其等价的DFA称为NFA确定化。其算法如下:
已知 A : N F A A:NFA A:NFA, 构造 A ’ : D F A A’:DFA A’:DFA。
-
令 A ’ A’ A’的初始状态为 I 0 ’ = ε _ C L O S U R E ( S 1 , S 2 , … S k ) I_0’=ε\_CLOSURE({S1,S2,…Sk}) I0’=ε_CLOSURE(S1,S2,…Sk),其中 S 1 … S k S1…Sk S1…Sk是 A A A的全部初始状态。
-
若 I = S 1 , … , S m I={S_1,…,S_m} I=S1,…,Sm是 A ’ A’ A’的一个状态, a ∈ ∑ a∈∑ a∈∑,则定义 f ’ ( I , a ) = I a f’(I, a)=I_a f’(I,a)=Ia,将 I a I_a Ia加入 S ’ S’ S’,重复该过程,直到 S ’ S’ S’不产生新状态。
-
若 I ’ = S 1 , … , S n I’={S_1,…,S_n} I’=S1,…,Sn是 A ’ A’ A’的一个状态,且存在一个 S i S_i Si是 A A A的终止状态,则令 I ’ I’ I’为 A ’ A’ A’的终止状态。
这个NFA确定化的过程如下:
- NFA的初始状态是1,该状态可以接收一个空闭包ε到状态2。因此DFA的初始状态是 {1,2}
- 由上可知DFA的初始状态是 {1,2},{1,2} 中的 1 接收输入字a可转换到 {4,5},而 {4,5} 接收空闭包到状态 {6,7},其中 6 还可以接收空闭包到状态 2。而 2 不能接收输入字 a。因此 {1,2} 接收输入字a可转换到 {2,4,5,6,7}。
- {1,2} 中的 1 不能接收输入字 b;2 接收输入字 b 到 状态3,状态 3 还可以接收空闭包到状态 8。因此 {1,2} 接收输入字b到状态 {3,8}。
- 进行如上三步后,DFA 中的状态有 {1,2}、{2,4,5,6,7}、{3,8},其中 {1,2} 状态转换后的状态已经算完。
- 接下来,我们再看DFA的状态 {2,4,5,6,7}。该状态不能接收输入字a;该状态中的2状态接收 b 到达 3 状态,该 3 状态接收空闭包还可到达8状态。其中的 6 状态和 7 状态均可接收输入字b到达9状态。于是DFA的状态中多了一个状态{3,8,9}。
- 我们再看DFA中状态{3,8}。其中的状态8接收输入字a可以到达状态9;状态{3,8}不能接收输入字b。因此 DFA 的状态增加一个状态{9}。
- 再来看状态{3,8,9},其中的状态8接收输入字a可以到达状态9;该状态不能接收输入字b。由于DFA中已经有状态{9},不再重复加入 DFA 的状态。
- 最后只有一个状态 {9} 了,该状态不能接收任何输入字。
- 总结出DFA中有状态 {1,2},{2,4,5,6,7},{3,8},{3,8,9},{9}。其中包含有NFA的终止状态 6 7 9 中任意一个状态的状态是DFA的终止状态。
表格如下:
| 状态 \ 输入字 | a | b |
|---|---|---|
| +{1,2} | {2,4,5,6,7} | {3,8} |
| -{2,4,5,6,7} | {} | {3,8,9} |
| {3,8} | {9} | {} |
| -{3,8,9} | {9} | {} |
| -{9} | {} | {} |
四 js中的正则
上面讲到的手机号码的验证规则中,你会发现跟我们在代码中写的正则表达式有所不同,在js中,电话号码的正则表达式为:
∧ 1 ( 3 [ 0 − 9 ] ∣ 5 [ 0 − 3 , 5 − 9 ] ) ∖ d { 2 } \wedge 1(3[0-9]|5[0-3,5-9])\setminus d\{2\} ∧1(3[0−9]∣5[0−3,5−9])∖d{2}$ (式1)
同样,下面这个正则表达式也能匹配到相同的结果:
∧ 1 ( 3 ∖ d { 3 } ∣ 5 [ 0 − 3 , 5 − 9 ] ∖ d { 2 } ) \wedge 1(3\setminus d\{3\}\mid 5[0-3,5-9]\setminus d\{2\}) ∧1(3∖d{3}∣5[0−3,5−9]∖d{2})$ (式2)
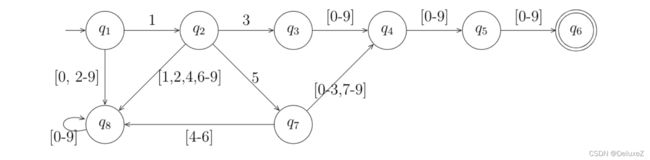
也就是说,我们同一个匹配需求,有多种不同的正则表达式都能达成。导致这种现象出现的主要原因是:自动机不一样。例如,电话号码的例子,我们绘制的自动机也有可能是这样的:

这个自动机对应的正则表达式即为式2。
上面式1的正则表达式跟我们前文讲的也有所不同,这是因为在不同语言中,对正则表达式又有不同的规则。比如:在真正的电话号码中,后8位为任意数字,那我们就需要写8次 [ 0 − 9 ] [0-9] [0−9],这也太麻烦了,要是写100次呢。所以出现了 ∖ d { 8 } \setminus d\{8\} ∖d{8}这个操作,表示任意数字重复8次。在不同语言中,引入了不同的修饰符、模式等定义,简化正则表达式的书写。js中,我们主要会用到以下定义:
| 符号 | 描述 |
|---|---|
| i | 执行对大小写不敏感的匹配。 |
| g | 执行全局匹配(查找所有匹配而非在找到第一个匹配后停止)。 |
| m | 执行多行匹配。 |
| [] | 查找方括号之间的任何字符。 |
| | | 查找任何从 0 至 9 的数字。查找任何以 |
| \d | 查找任何从 0 至 9 的数字。 |
| \s | 查找空白字符。 |
| \b | 匹配单词边界。 |
| \uxxxx | 查找以十六进制数 xxxx 规定的 Unicode 字符。 |
| n+ | 匹配任何包含至少一个 n 的字符串。 |
| n* | 匹配任何包含零个或多个 n 的字符串。 |
| n? | 匹配任何包含零个或一个 n 的字符串。 |