动态规划背包问题总结
文章目录
-
- 0-1背包
-
- 二维dp
- 一维dp
- 完全背包
-
- 二维dp
- 二维dp优化
- 一维dp
- 多重背包
-
- 多重背包二进制优化
- 多重背包单调队列优化
- 混合背包问题
- 二维费用的背包问题
- 分组背包问题
- 有依赖的背包问题
- 背包问题求方案数
- 背包问题求具体方案
参考:背包九讲(度娘自行搜索)
还有b站有个背包九讲的视频也讲的挺好的: 背包九讲专题_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
0-1背包
0-1背包,最简单直白的背包问题,但也是最重要的(因为后续很多种背包问题都会转化为0-1背包问题进行解答),每个物品只有选 / 不选两种选项。
0-1背包的各种类型(最大值/最小值,true/false,组合数/排列数)其实状态转移的逻辑都是相似的,无非就是取最优值的时候根据要求max()/min()/累加/取或等。
下面用到的题目在这儿都能找到:题库 - AcWing,就不一一贴链接了。
二维dp
先从暴力的二维dp入手,因为二维dp其实更容易理解,状态转移逻辑更加直白。
- 状态: 可选物品和背包容量
- 决策: 选 / 不选
- dp数组含义: d p [ i ] [ j ] dp[i][j] dp[i][j]表示,前i个物品,背包容量为j时,能够获取的最大价值
- 状态转移方程: 根据决策分类讨论,对于第 i 件物品,
不选: d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]
选: d p [ i ] [ j ] = d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] dp[i][j] = dp[i-1][j-v[i]] + w[i] dp[i][j]=dp[i−1][j−v[i]]+w[i]
这儿注意:当背包剩余容量j < v[i]时,只有不选一种决策,所以:
j >= v[i]时:
d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] ) dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−v[i]]+w[i])
j < v[i]时:
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i-1][j] dp[i][j]=dp[i−1][j]
那么代码逻辑就很明确了:
#include
#include
using namespace std;
const int N = 1010;
int v[N], w[N];
int dp[N][N];//定义在堆里,会默认初始化为0
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
for(int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
for(int i = 1; i <= n; ++i){
for(int j = 0; j <= m; ++j){
if(j >= v[i]) dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);
else dp[i][j] = dp[i-1][j];
}
}
cout << dp[n][m] << endl;
return 0;
}
循环的顺序是先循环物品,再循环容量,然后循环决策(选/不选)。其实后面的所有背包问题几乎都是这样的循环顺序,物品-容量-决策。
当然由于输入输出的特殊关系,所以可以一边输入一边处理,节省存储体积和价值的数组:
#include
#include
using namespace std;
const int N = 1010;
int dp[N][N];
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w;
for(int i = 1; i <= n; ++i) {
cin >> v >> w;
for(int j = 0; j <= m; ++j){
if(j >= v) dp[i][j] = max(dp[i-1][j], dp[i-1][j-v] + w);
else dp[i][j] = dp[i-1][j];
}
}
cout << dp[n][m] << endl;
return 0;
}
一维dp
观察二维dp代码,可以发现状态 d p [ i ] [ j ] dp[i][j] dp[i][j] 只与前一行的 d p [ i − 1 ] [ . . . ] dp[i-1][...] dp[i−1][...] 有关,所以可以进行状态压缩。
只涉及两行的数据,可以使用滚动数组进行优化,不过滚动数组的思路这儿就不涉及了,也很简单。
这儿直接压缩为一维的,先上代码:
#include
#include
using namespace std;
const int N = 1010;
int dp[N];//dp[j]表示容量为j的最大价值
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w;
for(int i = 1; i <= n; ++i) {
cin >> v >> w;
for(int j = m; j >= v; --j)//注意这儿是逆序的噢
dp[j] = max(dp[j], dp[j-v] + w);
}
cout << dp[m] << endl;
return 0;
}
第二个 for 循环的逆序处理,是为了防止只一次循环计算的值把上一次循环计算的值(还要使用)覆盖掉。如果不好理解的话,可以每次循环输出数组查看一下就可以啦。
所以,0-1背包问题,一维dp的时候需要逆序遍历背包容量。
完全背包
完全背包的每个物品数量无限,想选多少个(只要装得下)都可以。
还是举例:3. 完全背包问题 - AcWing题库

和01背包问题的区别在于每种物品不再是选/不选了,完全背包的物品可以选择任意个(0,1,2…),只要装得下,都可以选。那dp无非就是状态+选择进行搭配,完全背包就相当于01背包的选择变多了,其他方面都是一致的。
01背包只有两种选择的时候,我们取两种选择的较大值,那么完全背包有多种选择,我们也可以枚举每种选择,然后取众多选择里最优的那个。这就是完全背包的朴素解法,比较暴力但是容易理解。
二维dp
还是从暴力的二维dp入手:
- 状态: 可选物品和背包容量
- 决策: 选0/1/2/3… k个(k*nums[i] <= j)
- dp数组含义: d p [ i ] [ j ] dp[i][j] dp[i][j]表示,前i个物品,背包容量为j时,能够获取的最大价值
- 状态转移方程: 根据决策进行分类讨论,对于第 i 件物品,我们决策可以选 0/1/2/3… k 个 ,(k*nums[i] <= j)件。枚举每一个决策:
d p [ i ] [ j ] = m a x ( d p [ i ] [ j ] , d p [ i − 1 ] [ j − k ∗ v [ i ] ] + k ∗ w [ i ] ) dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k*w[i]) dp[i][j]=max(dp[i][j],dp[i−1][j−k∗v[i]]+k∗w[i])
其中k=0,1,2...k(k*v[i] <= j)。
#include
#include
using namespace std;
const int N = 1010;
int dp[N][N];
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w;
for(int i = 1; i <= n; ++i) {
cin >> v >> w;
for(int j = 0; j <= m; ++j){
for(int k = 0; k*v <= j; ++k)//多一层枚举
dp[i][j] = max(dp[i][j], dp[i-1][j-k*v]+k*w);
}
}
cout << dp[n][m] << endl;
return 0;
}
不过,这是一个效率很一般的dp策略。
二维dp优化
先上代码
#include
#include
using namespace std;
const int N = 1010;
int dp[N][N];
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w;
for(int i = 1; i <= n; ++i) {
cin >> v >> w;
for(int j = 0; j <= m; ++j){
if(j >= v) dp[i][j] = max(dp[i-1][j], dp[i][j-v] + w);
else dp[i][j] = dp[i-1][j];
}
}
cout << dp[n][m] << endl;
return 0;
}
可以发现这个代码,和01背包的二维dp代码几乎一模一样,唯一不同的点是第15行,此处是:
if(j >= v) dp[i][j] = max(dp[i-1][j], dp[i][j-v] + w);
01背包的是:
if(j >= v) dp[i][j] = max(dp[i-1][j], dp[i-1][j-v] + w);
等号右边的第二项第一个下标,一个是[i],一个是[i-1]。至于为什么,下一步会解释。这儿先来看一维的dp是什么样的。
一维dp
状态压缩至一维,还是先上代码:
#include
#include
using namespace std;
const int N = 1010;
int dp[N];//dp[j]表示容量为j的最大价值
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w;
for(int i = 1; i <= n; ++i) {
cin >> v >> w;
for(int j = v; j <= m; ++j)//注意这儿是正序的噢
dp[j] = max(dp[j], dp[j-v] + w);
}
cout << dp[m] << endl;
return 0;
}
同样可以发现该代码和0-1背包问题的一维dp代码特别像,事实上两处的代码只有一个地方不同:第二个循环。0-1背包的一维dp,第二个循环需要逆序处理,而完全背包的一维dp,第二个循环需要正序处理。
之前的逆序处理,是因为防止上一层的值被覆盖,那这儿就不怕上一层的值被覆盖掉吗?emm…还真不怕,而且覆盖掉才是我们真正需要的。至于为什么,比较抽象,我先贴一个背包九讲里面的解释:

两层解释,第一层文字解释看不懂没关系,下面说了公式可以推导出来,至于推导过程,是这样的:
来自:动态规划(完全背包问题,有公式推导) - 零钱兑换 II - 力扣(LeetCode)
这儿的推导针对的是完全背包的组合问题,但是文章开头说了,最值问题还是组合问题本质上状态转移逻辑是一致的。
最后再提一句,对于完全背包来说,其实两层 for 循环是可以颠倒的。
多重背包
多重背包问题是这样的:
和前两种背包问题还是很相似,只不过数量上加了一个限制,不可以无限选择,会有一个数量s进行限制,那么我们还是可以对选多少件物品进行枚举:
#include
#include
using namespace std;
const int N = 110;
int dp[N][N];
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w, s;
for(int i = 1; i <= n; ++i) {
cin >> v >> w >> s;
for(int j = 0; j <= m; ++j){
for(int k = 0; k <= s && k*v <= j; ++k)//多一层枚举,加一个s限制
dp[i][j] = max(dp[i][j], dp[i-1][j-k*v]+k*w);
}
}
cout << dp[n][m] << endl;
return 0;
}
可以发现代码和完全背包问题的第一个二维dp代码几乎一致,无非是第三层for循环里面加了一个数量s的限制。
可以进行空间压缩(需要逆序):
#include
#include
using namespace std;
const int N = 110;
int dp[N];
int main(){
int n, m;//物品数量、背包容量
cin >> n >> m;
int v, w, s;
for(int i = 1; i <= n; ++i) {
cin >> v >> w >> s;
for(int j = m; j >= 0; --j){
for(int k = 0; k <= s && k*v <= j; ++k)//多一层枚举,加一个s限制
dp[j] = max(dp[j], dp[j-k*v]+k*w);
}
}
cout << dp[m] << endl;
return 0;
}
不过也说了这种dp策略效率很一般,这一题数据量是100,三层for循环下来复杂度1e6,还能接受,但是下一题数据量提升到1000之后,三层for循环就会超时。
多重背包二进制优化
看这个问题:
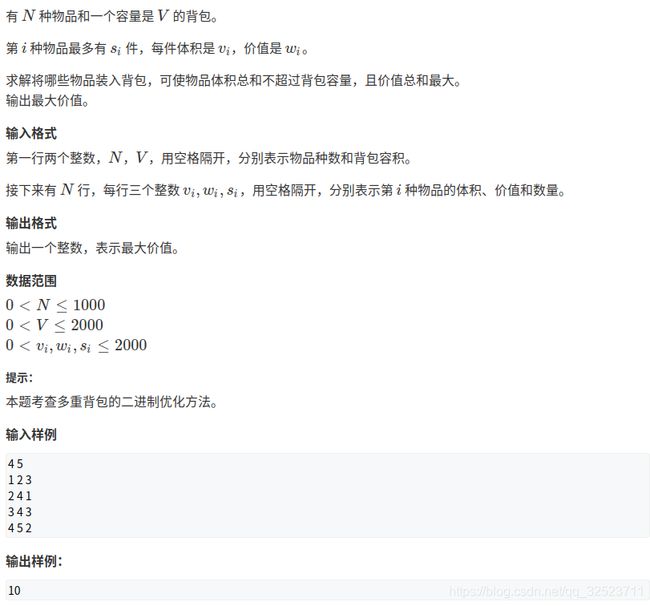
和上一个多重背包问题一样,唯一的区别是数据量由100变为1000,上面的代码就不能用了(超时)。
而且提示也说了,考察的是多重背包的二进制优化方法。
先别管什么是二进制优化方法,先想想怎样把一个多重背包问题转化为一个01背包问题呢?
我们可以每个数量s都全部拆开,比如第一个输入为:[4,5,3],表示体积为4,价值为5,最多有三件,那我们就把[4,5,3]拆开为3个[4,5,1]的物品[4,5],那么选择的过程中不就对应每一个物品都只有选/不选两种状态了吗?这样就成了01背包了。
但是实际上这样拆的复杂度也很高,因为s的数量级也是2000,所以虽然需要拆,但是不能这么拆。至于怎么拆,就涉及二进制优化了。
我们之前全部拆成一个一个的,这么拆原理上可行(但是复杂度太高)的原因是不管最后选择的是多少个,都可以由多个1组合而来,也就是可以被枚举出来。比如7个1,可以组成0-7之间的任何数。但是反过来想,要想组成0-7之间的任何数,需要7个因子吗?不需要,我们用3个数1,2,4就可以搭配出0-7之间的任何数,这就是二进制优化的思想。
所以二进制优化的重点就在于,怎样计算出这些因子(比如上面的1,2,4)。
整体拆的过程是这样的,假设对于i来说,初始输入分别为v[i],w[i],s[i],拆分之后体积、价值分别存储在数组a、b之中:
for (int j = 1; j <= s[i]; j <<= 1){//二进制拆分
a[total] = j * w[i]; //存价值
b[total] = j * v[i]; //存容量
++total;
s[i] -= j;
}
if (s[i] > 0){//拆到最后s[i]还 > 0;
a[total] = s[i] * w[i];
b[total] = s[i] * v[i];
++total;
}
代码的逻辑其实很简单,按照2的幂拆下去,知道不能拆为止,假设初始s = 7,那么:
j = 1, 1 <= 7,拆出一个1,s剩下7-1=6
j = 2, 2 <= 6,拆出一个2,s剩下6-2=4
j = 4, 4 <= 4,拆出一个4,s剩下4-4 = 0
最后,s = 0,退出循环(如果最后s不为0,就把剩余部分再作为一项)
此处s最大值为2000,2000 < 2^11,也就是说最多拆成11个。
拆分之后,就是01背包问题了,直接写一维dp(逆序):
#include
#include
using namespace std;
const int N = 2010;
int a[N*11], b[N*11];//最多拆分为11个(2^11 > 2000)
int dp[N];
int main()
{
int n, m; //物品数量、背包容量
cin >> n >> m;
int v, w, s, idx = 1;
for (int i = 1; i <= n; ++i){
cin >> v >> w >> s;
for(int j = 1; j <= s; j <<= 1){//二进制拆分
a[idx] = j*v;//容量
b[idx++] = j*w;//价值
s -= j;
}
if(s != 0){//拆到最后s[i]还 > 0;
a[idx] = s*v;
b[idx++] = s*w;
}
}
for(int i = 1; i <= idx; ++i){//01背包一维dp
for(int j = m; j >= a[i]; --j){
dp[j] = max(dp[j], dp[j-a[i]] + b[i]);
}
}
cout << dp[m] << endl;
return 0;
}
多重背包单调队列优化
怎么把单调队列和背包问题结合起来呢?

还是和之前一样的题目,但是数据量又大了一个量级,这个量级下二进制优化也倒下了。如果使用二进制优化,复杂度大概是o(NVlog(数量级)),上一题大概是10002000log(2000),大概是10^ 7量级,c++1s内能够计算的量级大概就是10^ 7。而这一题的数量级是200001000log(20000),大约是3*10^8量级,使用二进制优化会超时。(二进制优化的log均以2为底)
所以需要进行单调队列优化,将复杂度优化到o(N*V)量级。单调队列的思路可以看这题:leetcode 第 239 题:滑动窗口最大值(C++)_zj-CSDN博客
emmm…看了半天,自己还不是很理解,可以看这个:AcWing 6. 多重背包问题 III 详解 + yxc大佬代码解读 - AcWing
混合背包问题
混合的意思就是上面几种背包的混合,可能可以选无限次,可能只有选/不选,可能有个数限制:

那其实解决思路就是不同种类的物品,使用不同的选择策略进行转移就可以了:多重背包问题的话,先进行二进制拆分为01背包问题,所以最后其实就是处理两类:01背包和完全背包,采用各自的策略就可以了。
#include
#include
#include
using namespace std;
const int N = 1010;
int dp[N];
struct Thing{
int kind;
int v, w;
};
vector things;
int main(){
int n, m; //物品数量、背包容量
cin >> n >> m;
int v, w, s;
for (int i = 1; i <= n; ++i){
cin >> v >> w >> s;
if(s < 0) things.push_back({-1,v,w});//01背包
else if(s == 0) things.push_back({0, v, w});//完全背包
else{//多重背包问题,二进制分解
for(int j = 1; j <= s; j <<= 1){
things.push_back({-1, j*v, j*w});
s -= j;
}
if(s > 0) things.push_back({-1, s*v, s*w});
}
}
//至此所有的物品要么是01背包类型,要么是完全背包类型
for(const auto &thing : things){
if(thing.kind < 0){
for(int j = m; j >= thing.v; --j)//01背包逆序
dp[j] = max(dp[j], dp[j - thing.v] + thing.w);
}else{
for(int j = thing.v; j <= m; ++j)//完全背包正序
dp[j] = max(dp[j], dp[j - thing.v] + thing.w);
}
}
cout << dp[m] << endl;
return 0;
}
二维费用的背包问题
题目是类似的,但是每装一个物品,既占体积也占重量,不过本质上还是01背包问题,只不过多了一个状态。
解法都是类似的,只是求解的时候需要满足两个限制:容量和承受重量。
/*
dp[i][j]表示体积是i,重量是j的情况下的最大价值
*/
#include
#include
using namespace std;
const int N = 110;
int dp[N][N];
int main(){
int n, v, m;
cin >> n >> v >> m;
int a, b, c;//体积、重量、价值
for(int i = 0; i < n; ++i){
cin >> a >> b >> c;
for(int j = v; j >= a; --j){//01背包逆序,枚举体积
for(int k = m; k >= b; --k){//01背包逆序,枚举重量
dp[j][k] = max(dp[j][k], dp[j-a][k-b] + c);
}
}
}
cout << dp[v][m] << endl;
return 0;
}
LeetCode第 474 题:一和零(C++)_zj-CSDN博客,就是一个二维费用的01背包问题。
分组背包问题
其实这个也很简单,其实就是每组的决策就是s+1种(s为组内物品数量),按照01背包来做就行:
#include
#include
using namespace std;
const int N = 110;
int dp[N], v[N], w[N];//dp[i]表示前i组物品,能够获取的最大价值
int main(){
int n, m;//组数,容量
cin >> n >> m;
for(int i = 0; i < n; ++i){//枚举每一组
int s;
cin >> s;
for(int j = 0; j < s; ++j) cin >> v[j] >> w[j];
//因为组内元素互斥,所以必须先枚举容量再枚举分组物品,颠倒过来之后不能保证互斥
for(int j = m; j >= 0; --j){//枚举容量,01背包逆序
for(int k = 0; k < s; ++k){//枚举分组
if(j >= v[k]) dp[j] = max(dp[j], dp[j-v[k]] + w[k]);
}
}
}
cout << dp[m] << endl;
return 0;
}
有依赖的背包问题
物品之间存在依赖关系,可能是主件+附件的关系,主件可以单独选择,但是附件不可以。选择附件的时候必须同时选择它的主件。或者依赖关系呈现一颗树的形式,选择子结点就必须选择父结点。


这个选择思想好理解,但是怎么去选择很难实现。。。
首先直接来的话,我们可以先遍历树,生成每一种可能的策略,但是根据背包九讲里面说的:

所以去生成所有的策略是不太现实的,除非依赖关系很简单,比如这一题:购物单_zj-CSDN博客
参考:AcWing 10. 有依赖的背包问题(思路不同于dxc,但是个人感觉更好理解) - AcWing
所以总体的思路是分组背包+树形dp(在用动态规划求每个父节点的属性之
前,需要对它的各个儿子的属性进行一次动态规划式的求值。)。
#include
#include
#include
using namespace std;
const int N = 110;
int v[N], w[N], dp[N][N];//dp[i][j]表示选择结点i为子树的物品,容量<=j的情况获取的最大价值
int n, m, root;
vector g[N];//邻接表
//dfs在遍历到 x 结点时,先考虑一定选上根节点 x
void dfs(int x){//考虑以x为根节点的子树
for(int i = v[x]; i <= m; ++i) dp[x][i] = w[x];//根节点x必须选
for(int i = 0; i < g[x].size(); ++i){//遍历父节点x的子节点
int y = g[x][i];//子节点y
dfs(y);//对树自下而上遍历
//在进行下面的01背包决策之前,根节点x的所有子节点能够获取的最大价值dp[y][0 ~ j-v[x]]已经计算好了
//j的范围为v[x]~m, 因为事先肯定选择了v[x]
for(int j = m; j >= v[x]; --j){//01背包的逆序思路(容量)
//分给子树y的空间不能大于j-v[x],不然无法选根物品x
for(int k = 0; k <= j - v[x]; ++k){//枚举决策(k表示分给以y为根节点的子树的空间)
dp[x][j] = max(dp[x][j], dp[x][j-k] + dp[y][k]);//这一步很难理解。。。
}
}
}
}
int main(){
cin >> n >> m;
for(int i = 1; i <= n; ++i){//结点的标号从1开始
int p;//依赖的节点(父节点)
cin >> v[i] >> w[i] >> p;
if(p == -1) root = i;//记录根节点
else g[p].push_back(i);//如果不是根节点就加入邻接表,节点i的父节点是p
}
dfs(root);
cout << dp[root][m] << endl;
return 0;
}
不容易理解的是,上面的代码其实是可以选择到节点1,2,4,5的,修改背包容量为11就可以了。至于为什么能够选到,还是得打印出来dp表更容易理解。dfs(y)后面的两层for循环,其实就像是bfs填写dp表的过程,依次遍历分配给子树多大的空间,计算该空间下能够得到的最大价值。
假设输入为:
3 7
2 3 -1
2 2 1
3 5 1
那么其实很容易看出全部物品都选的话,容量刚好够,所以最大价值是10。
输出dp表:
0 0 0 0 0 0 0 0
0 0 3 3 5 8 8 10 //最后计算
0 0 2 2 2 2 2 2 //先计算
0 0 0 5 5 5 5 5 //再计算
计算过程其实是先计算出第二行,然后是第三行,最后通过下面两行计算出第一行(根节点对应行)。最后的dp[1][7] = dp[1][4] + dp[3][3] = 5 + 5 = 10,而dp[1][4] = dp[1][2] + dp[2][2] = 2 + 3 = 5。也就是说dp[1][4] = 选择根节点(消耗空间2) + 又分配空间2去选择节点2,而dp[1][7] = 选择了节点1、 2 (消耗空间4) + 又分配空间3去选择节点3。
所以上面才会说整个过程很像bfs的dp打表过程。
不得不说dfs递归的树形dp还是很难理解的,虽然最终都是转化为01背包求解,但是自下而上的树形dp确实用的很妙。
背包问题求方案数
背包问题求具体方案
LeetCode第 140 题:单词拆分 II(C++)_zj-CSDN博客