二叉树的遍历+二叉树的基本操作

---

二叉树的操作

一、 二叉树的存储

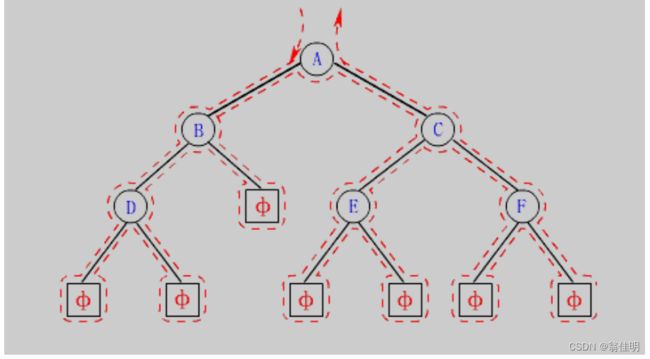
1.二叉树的存储结构

• 顺序存储
• 类似于链表的链式存储

// 孩子表示法
class Node {
int val; // 数据域
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
	int val; 
	Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
	Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
	Node parent; // 当前节点的根节点
}

二、 二叉树的基本操作

1.前置

创建一棵二叉树：

1. 定义结点

public class TestBinaryTree {
    static class  TreeNode{//
        public char val;//数据域
        public TreeNode left;//左孩子的引用
        public TreeNode right;//右孩子的引用

        public TreeNode(char val){//构造方法
            this.val = val;
        }
    }
      public TreeNode root;//二叉树的根节点
}

1.设置数据域，左右孩子的引用

2.设置构造方法

3.设置该树的根节点

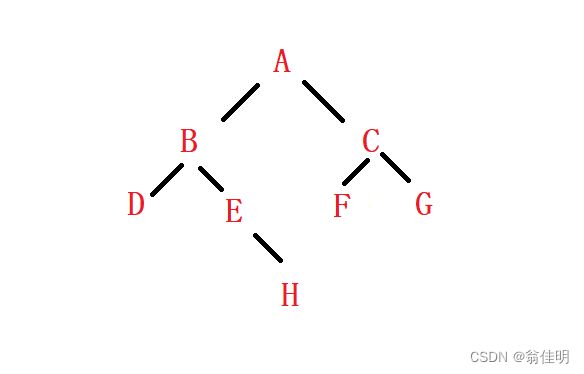
2.简单的创建二叉树

    public TreeNode creatTree(){//创建一个二叉树
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');
        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        E.left = H;
        C.left = F;
        C.right = G;
        return A;
    }

只是简单的手动创建二叉树，正确的写法在下文用递归完成

2.二叉数的遍历

1.前序遍历

根节点 -> 左子树 -> 右子树

1.遇到根节点，先打印根节点

2.根节点打印完，先打印左子树，左边打印完了，再打印右子树

3.每棵树都有根、左、右，子树中同样根据该顺序打印

ABDCEF

遍历思路：

    //前序遍历       先根，再左，后右
    //递归实现:
    public  void preOrder(TreeNode root){
        if (root==null){
            return ;
        }
        System.out.println(root.val);
        preOrder(root.left);
        preOrder(root.right);
    }

• 截止条件为结点等于空
• 如果不为空，打印根结点的值
• 递归子树，遇到空返回
• 把左子树递归完后，再进入右子树

子问题思路：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
         if (root==null){
            return res;
        }
        res.add(root.val);
        List<Integer> leftTree = preorderTraversal(root.left);
        res.addAll(leftTree);
        List<Integer> rightTree = preorderTraversal(root.right);
        res.addAll(rightTree);
        
        return res;

    }
}

2.中序遍历

左子树 -> 根节点 -> 右子树

先打印左子树，左子树打印完了，再打印根节点，最后打印右子树

    //中序遍历
    public  void inOrder(TreeNode root){
        if (root==null){
            return ;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

DBAECF

3.后序遍历

左子树 -> 右子树 -> 根节点

先打印左子树，再打印右子树，最后打印根节点

DBEFCA

    //后序遍历
    public  void postOrder(TreeNode root){
        if (root==null){
            return ;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }

4.层序遍历

按从左到右，从上到下的顺序

ABCDEF

• 前序遍历可以定位根的位置

• 中序遍历找到根，根的左边就是左子树，根的右边是右子树

• 只根据前序遍历和后续遍历不能创建一个二叉树，无法确定左右子树

3.二叉树的操作

1.获取树中节点的个数

时间复杂度 : o (N) 要遍历每一个结点

空间复杂度 ：o (log₂N) 开辟的内存 ~= 高度，开辟右树的时候，左树已经递归完了

(log₂N)->完全二叉树 单分支数：o(N)

子问题思路：左数的结点+右树的结点+1

    public int size(Node root) {
        if (root == null) {
            return 0;
        }
        int leftSize = size(root.left);
        int rightSize = size(root.right);
        return leftSize + rightSize + 1;
    }

结点为空返回0；

一个结点的左右子结点都为null,返回0+0+1 = 1，代表该子树的结点数

左子树结点数+右子树结点数+1 等于当前数的总结点数

遍历思路：遇见结点+1

    public int nodeSize = 0;

    public void size(TreeNode root) {
        if (root == null) {
            return 0;
        }
        nodeSize++;
        size(root.left);
        size(root.right); 
    }

结点不为空就+1

2.获取叶子节点的个数

    public int getLeafNodeCount(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right == null) {
            return 1;//遇到叶子结点，返回1
        }
        int leftSize = getLeafNodeCount(root.left);//递归返回左数的叶子结点个数
        int rightSize = getLeafNodeCount(root.right);//递归返回右数的叶子结点个数
        return leftSize + rightSize;
    }

子问题思路：

遇到叶子结点，返回1

递归找到底层的叶子结点，层层返回，左右子树分别包含的叶子结点数之和

    public static int leafSize;
    public void getLeafNodeCount2(TreeNode root) {
        if (root == null){
            return;
        }
        if (root.left ==null&& root.right==null){
            leafSize++;
        }
        getLeafNodeCount2(root.left);
        getLeafNodeCount2(root.right);
    }

递归思路，遇到符合的叶子结点，计数+1

3.获取第K层节点的个数

子问题思路：

    //获取第K层节点的个数
    public int getKLevelNodeCount(TreeNode root, int k) {
        if (root == null) {
            return 0;
        }
        if (k == 1) {
            return 1;
        }
        int liftSize = getKLevelNodeCount(root.left, k - 1);
        int rightSize = getKLevelNodeCount(root.right, k - 1);
        return liftSize + rightSize;
    }

1.求 root 的第 K 层结点 ==求左树的第K-1层结点 + 求右树的第K-1层结点

2.不断递归子树，当 K-1 为1时，所求的结点数的返回值之和 就为K层的结点个数

4.获取二叉树的高度

    // 获取二叉树的高度
    public int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight= getHeight(root.left);
        int rightHeight= getHeight(root.right);
        return (leftHeight > rightHeight) ? leftHeight + 1 : rightHeight + 1;
    }

1.求出左树的高度和右树的高度，返回两者中的最大值+1

2.root==null ，返回0

3.时间复杂度 o（N）, N为结点个数，每个结点在递归中只被遍历一遍

4.空间复杂度：o(height)，height为二叉树高度，递归函数需要栈空间，栈空间取决于递归的深度，空间复杂的==二叉树的高度

5.检测值为value的元素是否存在

思路：

1.前序遍历的方式遍历二叉树

2.判断每个结点的val值是否为value，符合返回当前结点

3.如果结点为空返回空，不为空判断是否符合

4递归左子树->递归右子树

5.递归返回的值可能是空的，再次判断

    // 检测值为value的元素是否存在
    public TreeNode find(TreeNode root, int val) {
        if (root == null) {//根节点为空返回空
            return null;
        }
        if (root.val == val) {//结点符合要求，返回结点
            return root;
        }
        TreeNode Left = find(root.left, val);//递归返回的值可能是空的
        if (Left != null) {
            return Left;
        }
        TreeNode Right = find(root.right, val);
        if (Right != null) {
            return Right;
        }
        return null;//没有找到
    }

点击移步博客主页，欢迎光临~