第一周所有搜索题解

目录

n皇后

自然数拆分

填涂颜色

PERKET

单词方阵 

kkksc03考前临时抱佛脚

Lake Counting S

马的遍历

奇怪的电梯

玉米迷宫

Meteor Shower

 单词接龙

---

n皇后

- [P1219 [USACO1.5]八皇后 Checker Challenge]([USACO1.5]八皇后 Checker Challenge - 洛谷)

我在这里想介绍一下如何用dfs解n皇后。

dfs一般会用到递归，所以首先我们应该确认递归参数，终止条件，递归搜索逻辑。

题目分析：递归参数很明显为行数row,终止条件即为row>输入的行数n,此时回溯。根据题目意思，在处理递归节点时，同一列不能放，对角线都不能放，同一行也不能放（但在实际操作中无需考虑）。同一列不能放很简单，直接用个一维数组记录即可。但对于对角线却需要转换一下。

图片来自于：biibii懒猫老师

​

 同一上对角线中，行号减去列号相等，也用一个数组来记录，但为了让所有下标都大于0，所以都加上一个n.

​

 同一下对角线中，行号加列号想等，且相加后所有下标大于等于0，所以无需加个n.

实现代码如下：

#include
int place[15];//栈，用来记录每一行皇后的位置
int flag[15],d1[30],d2[30];//d1为上对角线，d2为下对角线,0表示未被占据，非0表示已占据
int n,count,top;
void dfs(int row)
{
    if(row>n)//边界情况要>n，不是等于n
    {
        count++;
        if(count<=3)
        {
            for(int i=1;i<=top;i++)
            {
                printf("%d ",place[i]);
            }
            printf("\n");
        }
        return;
    }
    for(int i=1;i<=n;i++)//1至n列，尝试第row个皇后在第n列的可能性
    {
        if(!flag[i]&&!d1[row-i+n]&&!d2[row+i])
        {
            top++;
            place[top]=i;
            flag[i]=1;
            d1[row-i+n]=1;
            d2[row+i]=1;
            dfs(row+1);
            //回溯后取消标记
            flag[i]=0;
            d1[row-i+n]=0;
            d2[row+i]=0;
            top--;
        }
    }
}
int main()
{
    scanf("%d",&n);
    dfs(1);
    printf("%d",count);
    return 0;
}

自然数拆分

- [P2404 自然数的拆分问题](自然数的拆分问题 - 洛谷)

这题我同样用dfs解。

题目分析：这题的递归参数有两个，分别为加数位置number和剩下的数x。终止条件为x等于0且number>2,因为最少要两个数相加，然后回溯。在处理递归节点时，每一个加数应该大于等于它前一个加数。

所以代码如下：

#include
int a[10];//存加数
void dfs(int number,int x)//number为第几个加数位置，x为剩下的数
{
   if(x==0&&number>2)
   {
       for(int i=1;i=a[number-1])//此时a[0]=1发挥作用
       {
           a[number]=i;
           x-=i;
           dfs(number+1,x);
           //回溯
           a[number]=0;
           x+=i;
       }
   }
   return;
}
int main()
{
   int n=0;
   scanf("%d",&n);
   a[0]=1;
   dfs(1,n);
    return 0;
}

填涂颜色

填涂颜色：- [P1162 填涂颜色](填涂颜色 - 洛谷)

这其实是一道非常典型的连通块题目。我们用dfs来解。

题目分析：题目让我们·把闭合圈1内的0换成2，闭合圈1内的0难找，我们可以逆向思维，去找闭合圈外的0，并将其标记即可。不难发现，与边界0相通的0都是需要标记的，所以我们可以从边界0开始上下左右四个方向来搜索。注意这题不需要标记。

实现代码如下：

//把圈外的元素都搜一遍并赋值-1，从一点向四个方向搜索，越界或不等于0时停止
#include
int n;
int map[31][31];
void dfs(int x,int y)
{
    if(map[x][y]!=0||x<1||y<1||x>n||y>n)return;//换成map[x][y]==1没输出
    map[x][y]=-1;
    dfs(x+1,y);
    dfs(x,y-1);
    dfs(x-1,y);
    dfs(x,y+1);
}
int main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
            scanf("%d",&map[i][j]);
        }
    }
    //将四条边界中为0的分别搜索
    for(int i=1; i<=n; i++)
    {
        if(map[i][1]==0)dfs(i,1);
        if(map[i][n]==0)dfs(i,n);
        if(map[1][i]==0)dfs(1,i);
        if(map[n][i]==0)dfs(n,i);
    }
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
        {
            if(map[i][j]==-1)printf("0 ");
            if(map[i][j]==1)printf("1 ");
            if(map[i][j]==0)printf("2 ");
        }
        printf("\n");
    }
    return 0;
}

其实上面的dfs还有另一种写法，可能对于大家来说更熟悉一些。

void dfs(int x,int y)
{
    int next[4][2]= {{0,1},{1,0},{0,-1},{-1,0}};
    map[x][y]=-1;
    for(int i=0; i<4; i++)
    {
       int dx=x+next[i][0];
       int dy=y+next[i][1];
       if(map[dx][dy]!=0||x<1||y<1||x>n||y>n)continue;
       dfs(dx,dy);
    }
}

PERKET

PERKET：- [P2036 [COCI2008-2009#2] PERKET]([COCI2008-2009#2] PERKET - 洛谷)

这道题仍然可以用dfs解。

题目分析：求总酸度和总苦度的最小绝对差，可以分别用个一维数组来存着酸度和苦度，除此之外还需要用个book数组来记录每种调料是否使用过。

#include
#include
int sour[15],bitter[15],book[15],min=9999999;
int n,a=1,b;
void dfs(int x)
{
    if(x==n)return;
    for(int i=1;i<=n;i++)//搜索范围
    {

        if(book[i]==0)//没查找过的才操作
        {
            a*=sour[i];
            b+=bitter[i];
            if(min>abs(a-b))min=abs(a-b);
            book[i]=1;
            dfs(x+1);
            //回溯操作
            book[i]=0;
            a/=sour[i];
            b-=bitter[i];
        }
    }
}
int main()
{

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&sour[i],&bitter[i]);
    }
    dfs(0);
    printf("%d",min);
    return 0;
}

单词方阵 

单词方阵：- [P1101 单词方阵](单词方阵 - 洛谷)

题目分析：题目要我们保留"yizhong"单词，其他的改为'*’。我们先定义一个全是‘*’的答案数组，然后遍历整个单词方阵，如果遍历到了字母'y',那就往八个方向搜索。如果在某一方向上的字符串等于“yizhong”，那就把答案数组的相应位置改正“yizhong”即可。

实现代码如下：

#include
#include
char map[101][101],b[10]="yizhong",ans[101][101];
int next[8][2]= {{1,-1},{1,0},{1,1},{0,-1},{0,1},{-1,-1},{-1,0},{-1,1}};//移动模拟数组
int flag,n;
void dfs(int x,int y)
{
    for(int i=0; i<8; i++)//8个方向分别搜索
    {
        flag=1;//标记
        for(int j=1; j<=6; j++)
        {
            int dx=x+j*next[i][0];
            int dy=y+j*next[i][1];
            if(dx<0||dy<0||dx>n-1||dy>n-1||map[dx][dy]!=b[j])
            {
                flag=0;//标记该方向不行
                break;
            }

        }
        if(flag==1)
        {
            for(int j=0; j<=6; j++)
                ans[x+j*next[i][0]][y+j*next[i][1]]=map[x+j*next[i][0]][y+j*next[i][1]];
        }

    }
}
int main()
{
    scanf("%d",&n);
    getchar();
    for(int i=0; i

kkksc03考前临时抱佛脚

- [P2392 kkksc03考前临时抱佛脚]https://www.luogu.com.cn/problem/P2392

 因为kkksc03是双核,故单科最少总时间分配给两核的时间应尽量相同，将每科总时长的1/2记为背包容量，使用0-1背包思想解题，再用该科总时长-dp[总时长的1/2]即为该科的最少时间。

实现代码如下：

#include
int num[5],test[21],dp[1000],ans;
int main()
{
    for(int i=1; i<=4; i++)
    {
        scanf("%d",&num[i]);
    }
    for(int i=1; i<=4; i++)
    {
        int sum=0;
        for(int j=1; j<=num[i]; j++)
        {
            scanf("%d",&test[j]);
            sum+=test[j];
        }
        for(int j=1; j<=num[i]; j++)
        {
            for(int k=sum/2; k>=test[j]; k--)
            {
                dp[k]=dp[k]>(dp[k-test[j]]+test[j])?dp[k]:(dp[k-test[j]]+test[j]);//优化后0-1背包的写法
            }
        }
        ans+=(sum-dp[sum/2]);
        for(int j=1; j<=sum/2; j++)dp[j]=0; //非常重要，记得清0
    }
    printf("%d",ans);
    return 0;
}

Lake Counting S

Lake Counting S- [P1596 [USACO10OCT]Lake Counting S]https://www.luogu.com.cn/problem/P1596

题目分析：刚开始我一直看不懂题目的意思，经过朋友的解释后我忽然发现这就是一个连通块的题目，与染色题差不多。实际上就是要我们求W连通块的个数，需要注意的是在找到一个W的连通块后，需要将其全部标记，以防下次重新搜。

代码实现如下：

#include
char map[110][110];
int n,m,count;
int next[8][2]= {{1,-1},{1,0},{1,1},{0,-1},{0,1},{-1,-1},{-1,0},{-1,1}};//移动模拟数组
void dfs(int x,int y)
{
    map[x][y]='1';//标记这些W，以防下次被再次搜到
    for(int i=0; i<8; i++)
    {
        int dx=x+next[i][0];
        int dy=y+next[i][1];
        if(dx<1||dy<0||dx>n||dy>m-1||map[dx][dy]!='W')
            continue;
        dfs(dx,dy);

    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++)
        scanf("%s",map[i]);
    for(int i=1; i<=n; i++)
    {
        for(int j=0; j

马的遍历

马的遍历：- [P1443 马的遍历](马的遍历 - 洛谷)

说实话，我觉得这题和迷宫问题简直相差无几，都是求从一个点出发到另一个点的最短路径，直接照着迷宫的思路来就好了。特别注意的是马的移动有八个方向，我刚开始还以为是4个。

直接上手操作。

#include
#include
int m,n;
struct note
{
    int x;
    int y;
    int step;
};
struct note queue[160001];//bfs解
int next[8][2]={{2,1},{2,-1},{-2,1},{-2,-1},{1,2},{-1,2},{1,-2},{-1,-2}};
int book[401][401];
int main()
{
    int startx=0,starty=0;
    scanf("%d%d%d%d",&n,&m,&startx,&starty);
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            //起点入队
            int head=1,tail=1,flag=0;
            struct note point;
            point.x=startx;
            point.y=starty;
            point.step=0;
            queue[tail]=point;
            tail++;
            book[startx][starty]=1;
            while(headn||dy>m||book[dx][dy]==1)
                        continue;
                    struct note t;
                    t.x=dx;
                    t.y=dy;
                    t.step=queue[head].step+1;
                    queue[tail]=t;
                    tail++;
                    book[dx][dy]=1;
                }
                 //搜完出队
                head++;
            }
            if(flag==0)printf("%-5d",-1);
            memset(book,0,sizeof(book));

        }
        printf("\n");
    }
    return 0;
}

然后我就光荣的超时了，仔细一想，我上面的做法中多次从起点出发用广搜寻找目标点实属没必要。实际上用一遍广搜就可以了，不设终止条件，让他把能走的全部走完，然后用个答案数组存储相应位置所需要的步数即可，其他的则为-1.

修改后的代码：

#include
#include
int m,n;
struct note
{
    int x;
    int y;
    int step;
};
struct note queue[160001];
int next[8][2]= {{2,1},{2,-1},{-2,1},{-2,-1},{1,2},{-1,2},{1,-2},{-1,-2}};
int book[401][401];
int ans[401][401];
int main()
{
    memset(ans,-1,sizeof(ans));
    int startx=0,starty=0;
    scanf("%d%d%d%d",&n,&m,&startx,&starty);
    //不设终止条件，让他把能走的全部走完
    int head=1,tail=1;
    struct note point;
    point.x=startx;
    point.y=starty;
    point.step=0;
    queue[tail]=point;
    tail++;
    ans[startx][starty]=0;
    book[startx][starty]=1;
    while(headn||dy>m||book[dx][dy]==1)
                continue;
            struct note t;
            t.x=dx;
            t.y=dy;
            t.step=queue[head].step+1;
            queue[tail]=t;
            ans[dx][dy]=t.step;//用答案数组记录相应步数
            tail++;
            book[dx][dy]=1;
        }
        head++;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        printf("%-5d",ans[i][j]);//控制域宽
        printf("\n");
    }
    return 0;
}

奇怪的电梯

奇怪的电梯：- [P1135 奇怪的电梯](奇怪的电梯 - 洛谷)。

其实解这题依旧可以用到迷宫思路，只不过方向改为了上下。

直接上代码

#include
#include
int move[210],n,a,b,flag,min=9999999;
int book[210];
void dfs(int y,int step)
{
    if(y==b)
    {
        flag=1;
        if(min>step)min=step;
       return;
    }
    for(int i=1; i<=2; i++)
    {
        
        int dy=y+pow(-1,i)*move[y];
        if(dy<1||dy>n||book[dy]==1)
            continue;
        book[dy]=1;
        dfs(dy,step+1);
        book[dy]=0;
    }
}
int main()
{
    scanf("%d%d%d",&n,&a,&b);
    for(int i=1; i<=n; i++)
        scanf("%d",&move[i]);
    book[a]=1;
    dfs(a,0);
    if(flag==1)printf("%d",min);
    else printf("-1");
    
    return 0;
}

令人非常激动的是，我又超时了！在我苦恼了很久后我决定去看看别人的题解，然后我就发现了一个非常重要的神来之笔！

if(y==b)
    {
        flag=1;
        if(min>step)min=step;
    }
    if(step>min)return;

修改成上面之后通过只用了7ms!因为这样写可以直接过滤掉很多比现有次数长的分支！不用一路走下去！

玉米迷宫

玉米迷宫：- [P1825 [USACO11OPEN]Corn Maze S]([USACO11OPEN]Corn Maze S - 洛谷)

这是让我卡了整整一天的题目，虽然说思路不难，与普通迷宫类似，但是有些坑值得注意！

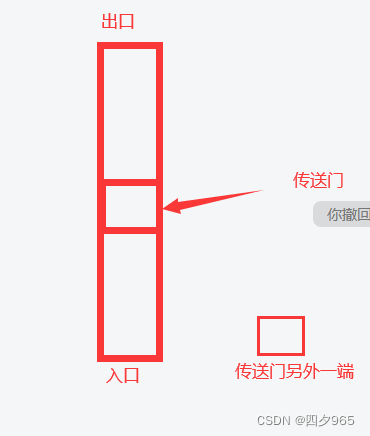
1.传送器不一定只用一次，有可能只是一个中转点，如下图：

你得走到传送门，传送到另一端，再在另一端随便走一步再回来，所以我们在标记时不能标记传送门的两端。

2.在走到传送门时，你需要遍历这个地图寻找对应的传送门，但请记住要避开原传送门坐标，只要x,y不全相等就可以了。！！！我当时一直认为x,y都得不相等，真被自己给蠢到了。

bfs解题代码如下：

#include
int n,m,startx,starty,endx,endy,dx,dy;
char map[310][310];
int book[310][310];
struct point
{
    int x;
    int y;
    int step;
};
void check(int *x,int *y)//寻找对应传送门
{
    for(int i=1; i<=n; i++)
    {
        for(int j=0; jn||dy<0||dy>m-1||book[dx][dy]==1||map[dx][dy]=='#')
                continue;
            if(map[dx][dy]>=65&&map[dx][dy]<=90)check(&dx,&dy);//传送
            queue[tail].x=dx;
            queue[tail].y=dy;
            queue[tail].step=queue[head].step+1;
            tail++;
            book[dx][dy]=1;
            if(map[dx][dy]>=65&&map[dx][dy]<=90)book[dx][dy]=0;//不能标记传送点的两端
        }
        head++;
    }
    return 0;
}

Meteor Shower

- [P2895 [USACO08FEB]Meteor Shower S]([USACO08FEB]Meteor Shower S - 洛谷)       

该题需要特别注意定义一个二维数组来记录流星坠落到每个格子的最早时间，如果该格子没有流星坠落则记为-1. 除此之外走过的格子当然也需要标记。其他的就是正常的迷宫做法。

   bfs解题代码如下：

#include
#include
struct point
{
    int x;
    int y;
    int time;
};
int droptime[310][310],book[310][310];
struct point queue[90100];
int next[4][2]= {{0,1},{1,0},{0,-1},{-1,0}};
int main()
{
    memset(droptime,-1,sizeof(droptime));//先全部记为不会坠落
    int m=0,xi=0,yi=0,ti=0;
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&xi,&yi,&ti);
        if(ti=0&&dy>=0&&(droptime[dx][dy]>ti||droptime[dx][dy]==-1))droptime[dx][dy]=ti;//取最早坠落时间
        }
    }
    int head=1,tail=1;
    queue[tail].x=0;
    queue[tail].y=0;
    queue[tail].time=0;
    book[0][0]=1;
    tail++;
    while(head=0&&dy>=0&&(droptime[dx][dy]>queue[head].time+1||droptime[dx][dy]==-1)&&book[dx][dy]==0)
            {
                book[dx][dy]=1;
                queue[tail].x=dx;
                queue[tail].y=dy;
                queue[tail].time=queue[head].time+1;
                tail++;
            }
        }
        head++;
    }
    return 0;
}

 单词接龙

单词接龙：- [P1019 [NOIP2000 提高组] 单词接龙]([NOIP2000 提高组] 单词接龙 - 洛谷)

需要注意的是这题每个单词可以最多出现两次，用个数组记录即可，接龙时可以有重合部分但不能存在包含关系，不然接了和没接是一样的。这题适合用dfs解。求重合部分可以从已经在龙里的最后一个单词（记为a）的最后面开始枚举（从后向前枚举）直到找到a单词的一个字母和想要接龙的单词(记为b)的第一个字母相等,把a单词中匹配到的相等字母的位置记录为j，然后a单词从j+1到尾进行循环枚举，同时b单词从头到后进行枚举，如果有不相等的一个字母就返回0，否则返回b的长度 -（k + 1）.

  代码实现如下：

   

#include
#include
char word[100][100];
int book[100],l[100];
int n,ans,max,p;
char start;
int check(int x,int y)//判断单词x,与单词y是否可接
{
    int lx=l[x];
    int ly=l[y];
    for(int i=lx-1;i>=0;i--)
    {
        if(word[x][i]==word[y][0])
        {
            int k=0;
            for(int j=i+1;j<=lx-1;j++)
            {
                k++;
                if(word[x][j]!=word[y][k])return 0;
            }
            return ly-k-1;
        }
    }
    return 0;
}
void dfs(int x)//x为龙尾，搜索可以接的单词
{
    if(ans>p)p=ans;
    for(int i=1;i<=n;i++)
    {
        if(book[i]<2&&check(x,i))
        {
            book[i]++;
            ans+=check(x,i);
            dfs(i);
            //回溯处理
            book[i]--;
            ans-=check(x,i);
        }
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%s",word[i]);
        l[i]=strlen(word[i]);
    }
    scanf(" %c",&start);
    for(int i=1; i<=n; i++)
    {
        if(word[i][0]==start)
        {
            ans+=l[i];
            book[i]++;
            dfs(i);
            //回溯处理
            book[i]--;
            ans-=l[i];
            if(max

洛谷有毒！！！我用

 getchar();
 scanf("%c",&start);

不给过！要想过只能用

scanf(" %c",&start);

总结：dfs牺牲时间换空间，bfs牺牲空间换时间。