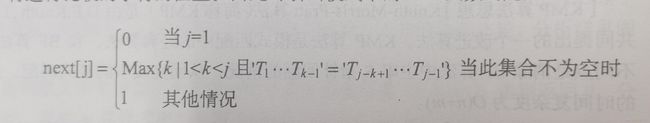第四章 串【数据结构与算法】【精致版】

前言

2023-11-3 15:47:38

以下内容源自《【数据结构与算法】【精致版】》
仅供学习交流使用

版权

禁止其他平台发布时删除以下此话
本文首次发布于CSDN平台
作者是CSDN@日星月云
博客主页是https://jsss-1.blog.csdn.net
禁止其他平台发布时删除以上此话

第4章串

4.1应用实例

文本编辑器

4.2串及其运算

4.2.1串的基本概念

1.串的概念
串（string）是由零个或多个字符组成的有限序列，一般记作：S=‘a₁a₂a₃…a_n’
其中
（1） S 为串的名字
（2）单引号括起来的字符串序列为串的值；将串值括起来的单引号本身不属于串，它的作用是避免串与常数与标识符混淆
（3）a_n（1≤i≤n）可以是字母、数字或其他字符
（4）n为串中字符的字数，称为串的长度。
2.常用术语
①空串
②空格串
③子串
④主串
⑤前缀子串
⑥后缀子串
⑦位置
⑧串相等
⑨模式匹配

4.2.2 串的基本运算

1.串的抽象数据类型定义
串的抽象数据类型定义如下。
ADT String{
数据对象:D={a_i,la_i∈CharacterSet,i=1,2,…,n,n>0}
数据关系:R={i-1|a,>la_i-1,a_i∈D,i=2,3,n}
基本操作:
(1) StrAssign(S,chars)
初始条件:chars是字符串常量。
操作结果:生成一个串S,并使其串值等于chars。
(2)StrCopy(S.T)
初始条件:串T存在
操作结果:将串T的值献给串S
(3) StrLength(S)
初始条件:串S存在
操作结果:返回串S的长度,即串S中字符的个数
(4) Strlnsert(S,pos,T)
初始条件:串S和T存在,I≤pos≤StrLength(S)+1
操作结果:在串S的第pos个字符之前插入串T
(5) StrDelete(S.pos,len)
初始条件:串S存在,1≤pos≤Strlength(S),且0≤len≤Sulengh(S)-pos+l
操作结果:在串S中删除从第pas个字符开始连续len个字符后形成的子串,
(6) StrCompare(S,T)
初始条件:串S和T存在。
操作结果:若串S和串了相等,则返回值等于0;否则返回串S和串下第一个不相等字符的ANSI码值之差
(7) StrCat(S,T)
初始条件:串S和T存在。S足够长
操作结果:将串T的值连接在串S的后面。
(8) SubString(T,S.pos.len）
初始条件:串S存在,1≤lpos≤StrLength(S),且0≤lensStrLength(S)-pos+1
操作结果:截取串S中从第pos个字符开始连续len个字符形成的子串,并赋值给串T,
(9) StrIndex(S,pos, T)
初始条件:串S和T存在,1≤pos≤StrLength(S):
操作结果:若串S中从第pos个字符后存在与串T相等的子串,则返回串T在申S中第pos个字符后首次出现的位置;否则返回0。
(10) StrReplace(S,T,V)
初始条件;串S、串T和串V存在,且串T是非空申。
操作结果:用串V替换串S中出现的所有与串T相等的不重叠的子串。
(11) StrEmpty(S)
初始条件:串S存在。
操作结果:若串S为空串,则返回TRUE;否则返回FALSE
(12) StrClear(S)
初始条件;串S存在
操作结果:将S清为空串，
(13) StrDestroy(S)
初始条件;串S存在
操作结果:销毁串S
}ADT Siring

4-1串的删除操作.c

#include
#include
#include
typedef struct String{
	char ch[MAXLEN+1];
	int len;
}String;

int StrLength(String S){
	if(S!=NULL){
		return S.len;
	}else{
		return 0;
	}
}

int StrCompare(String V,String T)  {
	return strcmp(V.ch,T.ch);
}

//【算法4-1】 串的删除操作 
//从串S中删除所有与T相同的字串
int Delete_Substring(String S, String T){ 
	int 1=1,n=0;
	while(i<=StrLength(S)-StrLength(T)+1){
	
		Substring(V,S,i,StrLength(T));	//求主串s从第i个字符起长度为串T长的子串V
		if(StrCompare(V,T)==0){			//子串v和T相等时，在串s中删除串T
			SubString(head,S,1,i-l);	//head是串s的前i-1个字符形成的子串
			SubString(tail,S,i+StrLength(T),StrLength(S)-i-StrLength(T)+1);
										//tail是串s中串T之后的字符所形成的子串
			StrCat(head,tail);			//将串tail连接在串head的后面
			StrAssign (S,head);			//使串s为删除子串T后的串值
			n++; 						//删除的次数累加
		}	else i++;
	}
	
	return n;							//返回删除的次数 
}

int main(){
	
} 

2. 串的基本运算示例

4.3串的存储结构及实现

4.3.1 定长顺序串

1.定长顺序串存储结构
定长顺序串存储结构如下:

#define MAXLEN 50//字符串的最大长度
typedef struct{
	char ch[ MAXLEN+1];//存储字符串的一维数组,每个分量存储一个字符,第0号单元不使用  
	int len;//字符串的长度
}SString;

串的实际长度可在预定义长度MAXLEN的范围内随意变动,超过MAXLEN,串值被舍去,称为“截断”

2.定长顺序串基本操作的实现

1-定长顺序串.c

#include
#include
#include 

//1.定长顺序串存储结构 

#define MAXLEN 50//字符串的最大长度 
typedef struct{
	char ch[MAXLEN+1];//存储字符串的一维数组，每一个分量存储一个字符，第0号单元不使用 
	int len;//字符串的长度 
} SString;
//建立串
//生成一个串，并且其串值等于chars 
void StrAssign(SString* S,char* chars){ 
	int len=strlen(chars);
	S->len=len;
	int i;
	for(i=0;i<len;i++){
		S->ch[i+1]=chars[i];
	}
//	Output(*S);
} 
//输出串
void Output(SString *S){
 	int i;
 	for(i=1;i<=S->len;i++){
		printf("%c",S->ch[i]);
	}
	printf("\n");
}

//(1)串插入函数 
//【算法4-2】串插入函数 
int SStrInsert(SString *S,int pos,const SString T){
	int i;
	if(NULL== S||NULL== S->ch||NULL==T.ch||pos<1||pos>S->len+1) {
		return 0;		//插入位置不合法 
	}


	if(S->len + T.len <= MAXLEN){//插入后串长小于等于MAXLEN，串T可以全部插入 
		for(i = S->len + T.len; i >=pos + T.len;i--)
			S->ch[i]= S->ch[i -T.len];
		for(i = pos; i < pos + T.len; i++)
			S->ch[i] =T.ch[i - pos+1];
		S->len = S->len+T.len;
	}else if(pos + T.len <= MAXLEN){ //插入后串长大于MAXLEN，串T可以全部插入 
		for(i = MAXLEN;i>= pos + T.len;i--)
			S->ch[i] = S->ch[i - T.len];
		for(i = pos; i < pos + T.len; i++)
			S->ch[i] = T.ch[i- pos+1];
		S->len = MAXLEN;
	}else{//插入后串长大于MAXLEN，串T的部分字符也可能被舍弃	 
		for(i = pos; i <= MAXLEN; i++)
			S->ch[i]=T.ch[i - pos + 1];
		S->len = MAXLEN;
	}
	return 1;
}


//(2)串删除函数
//【算法4-3】 串删除函数
int SStrDelete( SString * S,int pos, int len){
	int i=1;
	if(pos <1||pos >S->len || len <0|| len > S->len-pos+1){
		return 0;//删除参数不合法
	}
	for(i=pos;i<=S->len-len;i++){//移动元素
	 	S->ch[i]=S->ch[i+ len];
	}
	S->len=S->len-len;
	return 1;
}
//(3)串连接函数
//【算法4-4】 串连接函数
int SStrCat(SString * S, const SString T){
	int i=1;
	if(S->len+T.len<=MAXLEN){ //连接后非长小于等于MAXLEN
		for(i=S->len+1;i<=S->len+T.len;i++){
			S->ch[i]=T.ch[i-S->len];
		}		
		S->len=S->len+T.len;//更新串S的长度
		return 1;
	}else if(S->len<MAXLEN){//连接后中长大于 MAXLEN,且申S的长度小于MAXLEN
							//串T的部分字符被合弃
		for(i=S->len+1;i<=MAXLEN;i++){
			S->ch[i]=T.ch[i-S->len];
		}
		S->len=MAXLEN;
		return 0;
	}else{
		return 0;//串 S的长度等于 MAXLEN,串下不被连接
	}
		
}
//(4)求子串函数
//【算法4-5】 求子串函数 
int SubSString(SString * T,SString S,int pos,int len ){
	int i;
	if(len<0||len>S.len-pos+1||pos<1||pos>S.len){
		return 0;
	}
	for(i=1;i<=len; i++){
		T->ch[i]=S.ch[pos+i-1]; //提取pos之后的字符作为新串T
	}
	T->len=len;
	return 1 ;
}


 

int main(){
	SString *S;
	S=(SString*)malloc(sizeof(SString)); 
	char chars[MAXLEN];
	printf("输入chars:\n");
	gets(chars);
	printf("建立串：\n"); 
	StrAssign(S,chars);
	printf("输出串S：\n"); 
	Output(S); 
		
	SString *T;
	T=(SString*)malloc(sizeof(SString)); 
	StrAssign(T,chars);
	printf("输出串T：\n"); 
	Output(T);
	
	//串插入
	SStrInsert(S,2,*T);
	printf("在S[2]中插入T\n");
	Output(S);
	
	//串删除 
	SStrDelete(S,2,3);
	printf("在S[2]中删除长度为3的子串\n");
	Output(S);
	
	//串连接
	SStrCat(S,*T);
	printf("S连接T\n"); 
	Output(S);

	//求子串 
	SString *Z;
	Z=(SString*)malloc(sizeof(SString));  
	SubSString(Z,*S,2,3);
	printf("S[2]长度为3的子串\n"); 
	Output(Z);	
	
} 

通过以上的具体操作可以看出,在定长顺序串的操作中,可能出现串“截断”克服这种弊端,只有不限定串的最大长度,即动态分配串值的存储空间。

4.3.2 堆串

1.堆串存储结构

typedef struct{
	char * ch;//若是非空串,则指向串的起始地址;否则ch为NULL
	int len;//字符串的长度
}HString;

为了便于理解和讨论,这里在给串分配存储空间时,在实际串长的基础上多分配一个存储间，且连续空间的第0号单元不使用。

2.堆串基本操作的实现

2-堆串.c

#include
#include
#include 

typedef struct{
	char * ch;//若是非空串,则指向串的起始地址;否则ch为NULL
	int len;//字符串的长度
}HString;


//(1)串初始化函数
//【算法4-6】串初始化函数
void HStrInt(HString *S){	//初始化空串
	S->ch=NULL;			//将新定义的空串S的赋值为NULL
	S->len=0;			//将新定义的宝串S的长度设为0
}

//(2)串赋值函数
//【算法4-7】串赋值函数
int HStrAssign(HString *S,const char *chars){
	int i=0;
	while(chars[i]!='\0') i++;
	S->len=i; //串S的长度等于串chars的长度 
	if(0!=S->len){
		if(S->ch!=NULL) free(S->ch);
		S->ch=(char*) malloc((S->len+1)*sizeof(char));
		//0号单元不用，比实际需求多开辟一个空间 
		if(NULL==S->ch) return 0; //空间开辟失败
		for(i=1;i<=S->len;i++){
			S->ch[i]=chars[i-1];//将chars的内容注意赋给S->ch 
		} 

	} else{
		S->ch=NULL;
	}
	return 1;
}

//输出串
void Output(HString *S){
 	int i;
 	for(i=1;i<=S->len;i++){
		printf("%c",S->ch[i]);
	}
	printf("\n");
}


//(3)串插入函数 
//【算法4-8】 串插入函数 
int HStrInsert(HString * S, int pos, const HString T){
	int i;char* temp;
	if(pos>S->len||pos<1) return 0; //插入位置不合法
	temp=( char *)malloc((S->len+T.len+1)* sizeof( char));
	if(NULL==temp) return 0;
	for(i=1;i<pos;i++){				//把S串 pos(不含S->ch[pos])之前的字符赋给 temp
		temp[i]=S->ch[i];
	}
	for(i=pos; i<pos+T.len; i++){	//把 temp[pos :pos + T.len]之间的部分
		temp[i]=T.ch[i-pos+1];		//赋成串T的内容
	}
	for(i=pos +T.len;i<=S->len+T.len;i++){//把原 pos 之后的内容连接
		temp[i]=S->ch[i-T.len]; 	//到temp的尾部
	}
	free(S->ch); 
	S->ch=temp;
	S->len=S->len +T.len; 			//更新串S的长度
	return 1;
}


//(4)串删除函数
//【算法4-9】 串删除函数
int HStrDelete( HString * S,int pos,int len ){
	int i;char * temp;
	if(len<0||pos<1||pos>S->len-len+1)
		return 0;//删除位置不合法
	temp=(char*)malloc((S->len-len+1) *sizeof(char));
	if(NULL== temp) return 0;
	for(i=1;i<pos;i++) //把 S串 pos(不含 S->ch[pos])之前的字符复制给temp
		temp[i]=S->ch[i];
	for(i=pos;i<=S->len-len;i++) //把 temp[pos]之后的部分改写								 
		temp[i]=S->ch[i+len];	 //为S[pos+len:S->len]的内容
	
	free(S->ch);				 //这两句使得 temp替换S->ch 的位置
	S->ch=temp;
	S->len=S->len-len;			 //更新串 S的长度
	return 1;	
}

//(5)串连接函数
//【算法4-10】 串连接函数
int HStrCat(HString *S,const HString T){
	int i= 1;
	S->ch=(char *)realloc(S->ch,(S->len + T.len + 1)*sizeof(char));
								//函数 realloc 保留了串 S 原有的字符内容
	if(NULL==S->ch) return 0;
	for(i=S->len+1;i<=T.len+S->len; i++)
		S->ch[i]=T.ch[i- S->len];
	S->len=S->len+T.len;		//更新串 S的长度
	return 1;
}

//(6)求子串函数
//【算法4-11】求子串函数
int SubHString( HString * T, HString S, int pos , int len){
	int i=1;
	if(len<0||len>S.len-pos+1||pos<1||pos>S.len)
		return 0; //求子串参数不合法
	T->len=len;
	if(NULL!=T->ch) free(T->ch);
	T->ch=( char * )malloc( (T->len +1)* sizeof( char)) ;
	if(NULL==T->ch) return 0;
	for(i=1; i<=T->len; i++)
		T->ch[i]=S.ch[pos+i-1]; //提取 pos 之后的字符作为新串T
	return 1;
}

int main(){
	HString *S;
	S=(HString*)malloc(sizeof(HString)); 
	HStrInt(S);
	char chars[10];
	printf("输入chars:\n");
	gets(chars);
	printf("建立串：\n"); 
	HStrAssign(S,chars); 
	printf("输出串S：\n"); 
	Output(S);
	
	HString *T;
	T=(HString*)malloc(sizeof(HString)); 
	HStrInt(T);	
	HStrAssign(T,chars);
	printf("输出串T：\n"); 
	Output(T);	
	
	//串插入
	HStrInsert(S,2,*T);
	printf("在S[2]中插入T\n");
	Output(S);
	
	//串删除 
	HStrDelete(S,2,3);
	printf("在S[2]中删除长度为3的子串\n");
	Output(S);
	
	//串连接
	HStrCat(S,*T);
	printf("S连接T\n"); 
	Output(S);

	//求子串 
	HString *Z;
	Z=(HString*)malloc(sizeof(HString));  
	HStrInt(Z);	
	SubHString(Z,*S,2,3);
	printf("S[2]长度为3的子串\n"); 
	Output(Z);	
	
	
}

4.3.3 块链串

由于串是一种符殊的线性表,所以存储字符串的串值除了可以采用顺序存储结构，也可以用链式存储结构。

在串的链式存储结构中，链表的每个结点既可以存放一个字符,也可以存放多个字符，每个结点称为“块”,整个链表称为“块链结构”。

块链串存储结构如下:

3-块链串.c

#define BLOCK_SIZE 4//每个结点存放字符个数为4
typedef struct block{
	char ch[ BLOCK_SIZE];
	struct block * next;
} Block;
typedef struct{
	Block * head;//块链串的头指针
	Block * lail;//块链串的尾指针
	int len;//字符串长度
}LString;

4.4串的模式匹配

子串的定位操作是找子串在主串中从第 pos 个字符后首次出现的位置,又被称为“串的模式匹配"或“串匹配”,此运算的应用非常广泛。例如,在文本编辑程序中,经常要查找某一特定单词在文本中出现的位置。显然,解决此问题的有效算法能极大地提高文本编辑程序的响应性能在串匹配中,一般将主串S称为“目标串”,子串T称为“模式串”。

模式匹配的算法很多。本章仅讨论 BF模式匹配和KMP模式匹配这两种串匹配算法。

4.4.1 BF模式匹配算法

[BE算法思想]
Brute-Force 算法又称“蛮力匹配”算法(简称BP算法),从主串S的第pos个字符开始,和模式串了的第一个字符进行比较,若相等,则继续逐个比后续字符;否则回溯到主串的第 pos+1个字符开始再重新和模式串T进比较。以此类推,直至模式串了中的每一个字符依次和主串中的一个连的字符序列全部相等,则称模式匹配成功,此时返回模式串了的第一个字在主串S中的位置;否则主串中没有和模式串相等的字符序列,称模式匹配不成功。

[BF算法描述]
从主串S的第pos个字符开始的子串与模式串T比较的策略是从前到后依次进行比较。因此在主串中设置指示器i表示主串S中当前比较的字符;在模式串T中设置指示器j表示模式串T中当前比较的字符。

如图4-5所示,给出了一个匹配过程的例子,其中方框阴影对应的字符为主串S和模式串T比较时不相等的失配字符(假设 pos=1)。

从主串S中第pos个字符起和模式串T的第一个字符比较,若相等则继续逐个比较后续字符,此时i++;j++;否则从主串的下一个字符(i-j+2)和模式串的第一个字符(j=1)比较,分析详图4-6(a)。

当匹配成功时,返回模式串T中第一个字符相对于在主串的位置(i-T.en);否则返回0,分析详见图4-6(b),其中m是模式串的长度T.len。

4-12BF模式匹配算法

#include
#include
#include 

//1.定长顺序串存储结构 

#define MAXLEN 50//字符串的最大长度 
typedef struct{
	char ch[MAXLEN+1];//存储字符串的一维数组，每一个分量存储一个字符，第0号单元不使用 
	int len;//字符串的长度 
} SString;
//建立串
//生成一个串，并且其串值等于chars 
void StrAssign(SString* S,char* chars){ 
	int len=strlen(chars);
	S->len=len;
	int i;
	for(i=0;i<len;i++){
		S->ch[i+1]=chars[i];
	}
//	Output(*S);
} 
//输出串
void Output(SString *S){
 	int i;
 	for(i=1;i<=S->len;i++){
		printf("%c",S->ch[i]);
	}
	printf("\n");
}

int Index(SString S,int pos,SString T){
	int i=pos,j=1;//主串从第pos开始,模式串从头开始
	while (i<=S.len&&j<=T.len){
		if(S.ch[i]==T.ch[j]){//当对应字符相等时,比较后续字符
			i++;
			j++;
		}
		else{				//当对应字符不等时
			i=i-j+2;			//主串回溯到j-j+2的位置重新比较
			j=1;				//模式串从头开始重新比较
		}
	}
	if(j>T.len)	return i-T.len;	//匹配成功时,返回匹配起始位置
	else return 0;				//匹配失败时,返回0
}

int main(){
	SString S;
	char chars1[MAXLEN]={'a','b','a','b','c','a','b','c','a','c','b','a','b'};
	StrAssign(&S,chars1);
	Output(&S);
	
	SString *T;
	T=(SString*)malloc(sizeof(SString)); 
	char chars2[MAXLEN]={'a','b','c','a','c'};
	StrAssign(T,chars2);
	Output(T);	
	
	int ix=Index(S,1,*T);
	printf("%d",ix);//6
}

[BF算法分析]
BF算法的思想比较简单,但当在最坏情况下时,算法的时间复杂度为0(n×m),其中n和m分别是主串和模式的长度。这个算法的主要时间耗费在失配后的比较位置有回溯,因而造成了比较次数过多。为降低时间复杂度可采用无回溯的算法。

4.4.2 KMP模式匹配算法

[KMP算法思想]
Knuth-Morris-Pratt算法(简称KMP),是由DEKnuthJ.HMorris和V.RPratt 共同提出的一个改进算法。KMP算法是模式匹配中的经典算法,和BF算法相比,KMP算法的不同点是消除了 BF算法中主串S指针i回溯的情况。改进后算法的时间复杂度为0(n+m)。

[KMP算法描述]
KMP算法中,每当一趟匹配过程中出现字符比较不等时,主串S中的指针不需回溯,而是利用已经得到的“部分匹配”结果将模式串向右“滑动”尽可能远的一段距离后,继续进行比较。

回顾图4-5的匹配过程示例,在第三趟匹配中,当i=7、j=5字符比较不等时,又从i=4.j=1重新开始比较。然而,经过仔细观察可发现,在i=4和j=1,i=5和j=1以及i=6和j=1这三次比较都是不必进行的。因为从第三趟部分匹配的结果就可得出,主串中第4、5、6个字符必然和模式串中的第2.3.4个字符相等,即都是’bca。因为模式串中的第一个字符是’a’,因此它无须再和这三个字符进行比较,而仅需将模式串向右滑动三个字符的位置继续进行i=7.j=2时的字符比较即可。同理,在第一趟的匹配中出现字符不等时,仅需将模式向右移动两个字符的位置进行i=3、j=1时的字符比较。因此,在整个匹配的过程中，指针没有回溯,如图4-7所示。

一般情况下，假设主串为’S₁S₂…S_n’,模式串为’T₁T₂…T_n’，从上例的分析可知，为了实现KMP算法，需要解决以下问题，当匹配过程中产生“失配”(即S_i≠T_i)时，模式串“向右滑动”可滑动的距离有名远，也就是说，当主串中字符S_i,与模式串中字符T_j"失配”时，主串中字符S_i( i 指针不回溯)应与模式串中哪个字符再进行比较?

假设此时主串中字符S_i应与模式中字符T_k(k S=S₁S₂…S_i-j+1S_i-j+2…S_i-k+1…S_i-1S_i …S_n
T=            T₁    T₂    …T_j-k+1…T_j-k+2…
T=                               T₁     …T_k-1…

可以看出，若模式串中存在’T₁T₂…T_k-1’=‘T_j-k+1T_j-k+2…T_j-1’,且满足1i≠T_j 时，仅需将模式串向右滑动至第k个字符和主串中第i个字符对齐，匹配仅需从S_i、T_k的比较起继续进行，无需i指针的回溯。在匹配过程中为了尽可能“滑动”远一段的距离，因而应选择满足条件较大的k值。

若令next[j]=k，则next[]表明当模式中第j个字符与主串中相应字符“失配”时，在模式中需重新和主串中该字符进行比较的字符的位置。由此可引出模式串的next函数的定义:

由此可见next函数的计算仅和模式串本身有关，而和主串无关。其中’T₁T₂…T_k-1’是’T₁T₂…T_j-1‘’ 的真前缀子串,'T_j-k+1T_j-k+2…T_j-1’是’T₁T₂…T_j-1’的真后缀子串。当next函数定义中的集合不为空时 next[j]的值等于串’T₁T₂…T_j-1’的真前缀子串和真后缀子串相等时的最大子串长度+1。

通过以上分析，推导出模式串’abaabcac’的next值的计算过程如表4.1所示。
(1)当j=1时，由定义得知，next[1]=0;
(2)当j=2时，满足1

模式串’abaabcac’的next函数值如图4-8所示。

在求得模式串的next函数之后,匹配可如下进行:假设以指针i和j分别指示主串S和模式串T中当前比较的字符,令i的初始值为pos,j的初始值为1。若在匹配过程中S_i=T_i,，则i和j分别增1;否则，i不变,而j退到 next[j]的位置再比较(即S_i和T_next[j]进行比较),若相等,则指针各自增1,否则j再退到下一个next值的位置,以此类推,直至下列两种可能:一种是j退到某个next值(next[next[···next[j]]])时字符比较相等,则指针各自增1继续进行匹配；另一种是j退到next值为0(即与模式的第一个字符“失配”),则此时需将主串和模式串都同时向右滑动一个位置(此时j=0,当向右滑动一个位置时,即模式串的第一个字符),即从主串的下一个字符S_i+1和模式T_i重新开始比较。图4-9是KMP匹配过程的一个例子(假设pos=1)

[算法4-13]KMP模式匹配算法

int Index_KMP(SString S, int pos, SString T){
	int i=pos,j=1;						//主串从第pos开始,模式串从头开始
	while(i<=S.len && j<=T.len){
		if(j==0||S.ch[i]==T.ch[j]){		//继续比较后续宇符
			++i;++j;
		}else{
			j=next[j];					//模式串向右滑动
		}
	}
	if(j>T.len) return i-T.len;			//匹配成功时,返回匹配的起始位置
	else return 0;						//匹配失败时，返回0
}

[next算法描述]
KMP算法是在已知模式next函数值的基础上执行的,那么,如何求得模式串的next函数值呢?

由定义可知next[1]=0,假设next[j]=k,这表明在模式串中存在’T₁T₂···T_k-1’='T_j-k+1T_j-k+2···T_j，这样的关系,其中k为满足1next[j+1]的值可能有以下两种情况。

(1)若T_j=T_k则表明在模式串中’T₁T₂···T_k-1’=‘T_j-k+1T_j-k+2···T_j’

T=T~1~ ··· T~j-k+1~	···	T~j-1~ T~j~ ··· T~m~
					   	        =
T=		    T~1~    ···	T~k-1~ T~k~···
			长度为k

这就是说next[j+1]=k+1，即next[j+1]=next[j]+1。

(2)若T_j≠T_k则表明在模式串中’T₁T₂···T_k-1’≠’T_j-k+1T_j-k+2···T_j’

此时可将求next函数值的问题看成是一个模式匹配的问题,整个模式串既是主串又是模式串其中1

T=T~1~ ··· T~j-k+1~	··· T~j-k'+1~ ···	T~j-1~ T~j~ ··· T~m~
					   	        ≠
T=		    T~1~    ···	T~k-k'+1~ ···   T~k-1~  T~k~ ···
T=					    T~1~     ···	T~k'-1~ T~k'-next[k]~

①若T_j=T_k’,且k’=next[k],则next[j+1]=k’+1,即next[j+1]=next[k]+1,也相当于next[j+1]=next[next[j]]+1。
②若T_j≠T_k’则继续比较T_j和T_next[k’]即比较T_j和T_{next[next[k]]}
······
然后一直重复下去,若直到最后j=0时都未比较成功,则next[j+1]=1。

通过以上分析,计算第j+1个字符的 next 值时,需看第j个字符是否和第j个字符的next值指向的字符相等。

由此推导出模式串T=abaabcac的next值计算过程如下。
①当j=1时,由定义得知,next[1]=0。

j=1
T=a
n=0

②当j=2时,满足1

j=12
T=ab
n=01

③当j=3时,由于T₂≠T₁,且next[1]=0,则next[3]=1。

j=12345678
T=abaabcac
n=011
T~2~ ≠ T~next[2]~	(T~1~)
T~2~ ? T~next[1]~	(0)
next[3]=1

④当j=4时,由于T₃=T₁则next[4]=next[3]+1,即next[4]=2。

j=12345678
T=abaabcac
n=0112
  
T~3~ = T~next[3]~	(T~1~)
next[4]=next[3]+1

⑤当j=5时,由于T₄≠T₂,且next[2]的值是1,故继续比较T₄和T₁,由于T₄=T₁,则next[5]=next[2]+1,即next[5]=2。

j=12345678
T=abaabcac
n=01122
  
T~4~ ≠ T~next[4]~	(T~2~)
T~4~ = T~next[2]~	(T~1~)
next[5]=next[2]+1

⑥当j=6时,由于T₅=T₂,则next[6]=next[5]+1,即next[6]=3。

j=12345678
T=abaabcac
n=011223
  
T~5~ = T~next[5]~	(T~2~)
next[6]=next[5]+1

⑦当j=7时,由于T₆≠T₃,且next[3]的值是1,故继续比较T₆和T₁,由于T₆≠T₁,且 next[1]=0,则next[7]=1。

j=12345678
T=abaabcac
n=0112231
  
T~6~ ≠ T~next[6]~	(T~3~)
T~6~ ≠ T~next[3]~	(T~1~)
T~6~ ? T~next[1]~	(0)
next[7]=1

⑧当j=8时由于T₇=T₁,则next[8]=next[7]+1,即next[8]=2。

j=12345678
T=abaabcac
n=01122312
  
T~7~ = T~next[7]~	(T~1~)
next[8]=next[7]+1,

故得出该模式串的next值如图4-8所示。

j=12345678
T=abaabcac
n=01122312

[算法4-14]next算法

void Get_Next(SString T, int next[]){
	int j=1,k=0;
	next[1]=0;
	while(j<T.len){
		if(k==0||T.ch[j]==T.ch[k] ){
			++j;
			++k;
			next[j]=k;
		}else{
			k=next[k];
		}
	}
}

[nextval算法描述]

上述定义的next函数在某些情况下尚有缺陷。假设主串为’aaabaaaab’模式串为’aaaab’，则模式串对应的next函数值如下所示。

在求得模式串的next值之后,匹配过程如图4-10(a)所示。

从串匹配的过程可以看到,当i=4,j=4时,S₄不等于T₄,由next[j]所示还需进行i=4、j=3;i=4、j=2;i=4、j=1这三次比较。实际上,因为模式申中的第1,2,3个字符和第4个字符都相等(即都是a)因此,不需要再和主串中第4个字符相比较,而可以将模式一次向右滑动4个字符的位置直接进行i=5、j=1的字符比较。

这就是说,若按上述定义得到next[j]=k,而模式串中T_j=T_k,则当S_i≠T_j时,不需要进行S_i和T_k的比较,直接和T_next[k]进行比较;换句话说,此时的next[j]的值应和next[k]相同,为此将next[j]修正为nextval[j]。而模式串中T_j≠T_k则当S_i≠T_j时，还是需要进行S_i和T_k的比较,因此nextval[j]的值就是k,即nextval[j]的值就是next[j]的值。

通过以上分析,计算第j个字符的 nextval值时,要看第j个字符是否和第j个字符的next指向的字符相等。若相等,则nextval[j]=nextval[next[j]];否则,nextval[j]=next[j]。由此推出模式串T='aaaab’的nextval值计算过程如下。

①当j=1时,由定义得知,nextval[1]=0。
②当j=2时,由nex[2]=1,且 T₂=T₁,则nextval[2]=nextval[1],即nextval[2]=0。
③当j=3时,由next[3]=2,且T₃=T₂,则nextval[3]=nextval[2],即nextval[3]=0。
④当j=4时,由next[4]=3,且T₄=T₃则nextval[4]=nextval[3],即nextval[4]=0。
⑤当j=5时,由next[5]=4,且T₅≠T₄,则nextval[5]=next[5],即nextval[5]=4。

模式串’aaaab’的nextal函数值如下所示。

在求得模式串的nextval值之后,匹配过程如图4-10(b)所示。

求nextval函数值有两种方法,一种是不依赖next数组值,直接用观察法求得;另一种方法是如上所述的根据next数组值进行推理,在这里仅介绍第二种方法。

[算法4-15] nextval算法

void Get_NextVal(SString T, int next[] ,int nextval[]){
	int j=2,k=0;
	Get_Next(T,next);//通过算法4-14获得T的next值
	nextval[1]=0;	
	while (j<=T.len){
		k=next[j];
		if(T.ch[j]==T.ch[k]) nextval[j]=nextval[ k];
		else nextval[j]=next[j];
		j++;
	}
}

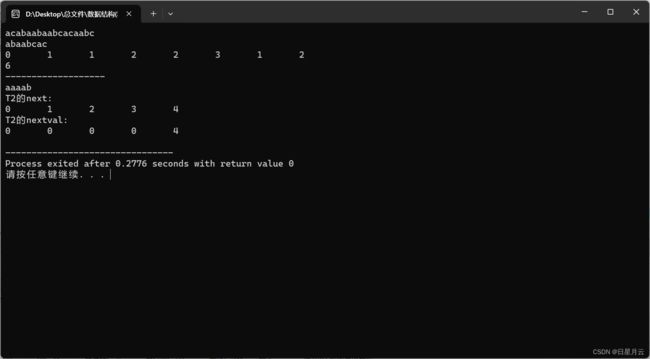
4-13KMP模式匹配算法.c

#include
#include
#include 

//1.定长顺序串存储结构 

#define MAXLEN 50//字符串的最大长度 
typedef struct{
	char ch[MAXLEN+1];//存储字符串的一维数组，每一个分量存储一个字符，第0号单元不使用 
	int len;//字符串的长度 
} SString;
//建立串
//生成一个串，并且其串值等于chars 
void StrAssign(SString* S,char* chars){ 
	int len=strlen(chars);
	S->len=len;
	int i;
	for(i=0;i<len;i++){
		S->ch[i+1]=chars[i];
	}
//	Output(*S);
} 
//输出串
void Output(SString *S){
 	int i;
 	for(i=1;i<=S->len;i++){
		printf("%c",S->ch[i]);
	}
	printf("\n");
}

int next[MAXLEN];

//【算法4-13】KMP模式匹配算法
int Index_KMP(SString S, int pos, SString T){
	int i=pos,j=1;						//主串从第pos开始,模式串从头开始
	while(i<=S.len && j<=T.len){
		if(j==0||S.ch[i]==T.ch[j]){		//继续比较后续宇符
			++i;++j;
		}else{
			j=next[j];					//模式串向右滑动
		}
	}
	if(j>T.len) return i-T.len;			//匹配成功时,返回匹配的起始位置
	else return 0;						//匹配失败时，返回0

}


//【算法4-14】next算法
void Get_Next(SString T, int next[]){
	int j=1,k=0;
	next[1]=0;
	while(j<T.len){
		if(k==0||T.ch[j]==T.ch[k] ){
			++j;
			++k;
			next[j]=k;
		}else{
			k=next[k];
		}
	}
}

//【算法4-15】 nextval算法
void Get_NextVal(SString T, int next[] ,int nextval[]){
	int j=2,k=0;
	Get_Next(T,next);//通过算法4-14获得T的next值
	nextval[1]=0;	
	while (j<=T.len){
		k=next[j];
		if(T.ch[j]==T.ch[k]) nextval[j]=nextval[ k];
		else nextval[j]=next[j];
		j++;
	}
}

int main(){
	SString S;
	char chars1[MAXLEN]={'a','c','a','b','a','a','b','a','a','b','c','a','c','a','a','b','c'};
	StrAssign(&S,chars1);
	Output(&S);
	
	SString *T;
	T=(SString*)malloc(sizeof(SString)); 
	char chars2[MAXLEN]={'a','b','a','a','b','c','a','c'};
	StrAssign(T,chars2);
	Output(T);	
	
	Get_Next(*T,next); 
	for(int i=1;i<=T->len;i++){
		printf("%d\t",next[i]);
	}
	printf("\n");
	
	int ix=Index_KMP(S,1,*T);
	printf("%d\n",ix);//6	
	
	
	printf("-------------------\n"); 
	SString *T2;
	T2=(SString*)malloc(sizeof(SString)); 
	char chars3[MAXLEN]={'a','a','a','a','b'};
	StrAssign(T2,chars3);
	Output(T2);		
	
	int nextval[T2->len+1];
	Get_NextVal(*T2,next,nextval); 
	printf("T2的next:\n"); 
	for(int i=1;i<=T2->len;i++){
		printf("%d\t",next[i]);
	}
	printf("\n");
	printf("T2的nextval:\n");
	for(int i=1;i<=T2->len;i++){
		printf("%d\t",nextval[i]);
	}
	printf("\n");
		
} 

[KMP算法分析]

KMP算法是在已知模式的 next或nextval的基础上执行的,如果不知道它们两者之一,则没有办法使用KMP算法。虽然有next和 nextval之分,但它们表示的意义和作用完全一样,因此在已知next或nextval进行匹配时,匹配算法不变。

通常模式串的长度m比主串的长度n要小很多且计算next或nextval函数的时间复杂度为0(m)。因此,对于整个匹配算法来说,所增加的计算next或nextval是值得的。

BF算法的时间复杂度为0(nxm),但是实际执行中m往往是远远小于n的,故近似于0(n+m),因此至今仍被采用。KMP算法仅当模式串与主串之间存在许多“部分匹配”的情况下,才会比 BF算法快。KMP算法的最大特点是主串的指针不需要回溯,整个匹配过程中,主串仅需从头到尾扫描一次,对于处理从外设输入的庞大文件很有效,可以边读边匹配。

4.5实例分析与实现

4.5.1串的实例分析

略

4.5.2简单文本编辑软件的实现

略

4.6算法总结

(1)字符串是一种特殊的线性表，器特殊性在于组成线性表的数据元素仅是一个单字符
(2)字符串常用的存储方式有定长顺序串、堆串和块链串三种。
(3)顺序串是以一维数组作为存储结构，其运算实现方法类似于线性表的顺序存储结构
(4)堆串是以动态一维数组作为存储结构,其运算实现方法和顺序串在存储管理上有所不同。
(5)块链串以链表作为存储结构，其运算实现方法类似于链表。
(6)串的模式匹配算法是本章的难点，BF模式匹配算法处理思路简单,但由于需要进行失配后主串回溯的处理，故而时间复杂度较高。改进的KMP模式匹配算法计算失配后模式串向右滑动的最大位置，由于失配后无回溯，故而匹配速度较高。

习题

练习计算next

abaabcac
01122312

aaaab
01234

abaabcabc
011223123

ababcabaababb
0112312342345

abcabaa
0111232

abcaabbabcabaacbacba
01112231234532211211

4(1)假定下面所有的串均是顺序串,参数 ch，ch1和 ch2均是字符型,编写下列算法。

①将串r中所有其值为ch1的字符换成 ch2的字符
②将串r中所有字符按照相反的次序仍存放在r中
③从串r中删除其值等于 ch 的所有字符。
④从串中第index 个字符起求出首次与串r2相同的子串的起始位置。

#include
#include
#include 

//1.定长顺序串存储结构 
#define MAXLEN 50//字符串的最大长度 
typedef struct{
	char ch[MAXLEN+1];//存储字符串的一维数组，每一个分量存储一个字符，第0号单元不使用 
	int len;//字符串的长度 
} SString;
//建立串
//生成一个串，并且其串值等于chars 
void StrAssign(SString* S,char* chars){ 
	int len=strlen(chars);
	S->len=len;
	int i;
	for(i=0;i<len;i++){
		S->ch[i+1]=chars[i];
	}
//	Output(*S);
} 
//输出串
void Output(SString *S){
 	int i;
 	for(i=1;i<=S->len;i++){
		printf("%c",S->ch[i]);
	}
	printf("\n");
}
 
//4.(1)①
//用v替换所有的t 
void charReplace(SString *S,char t,char v){
	int i;
	for (i=1;i<=S->len;i++){
		if(S->ch[i]==t){
			S->ch[i]=v; 
		}
	}
}

//4.(1)② 
//将S翻转 
void StringReserve(SString *S){
	int i;
	for (i=1;i<=S->len/2;i++){
		int j=S->len-i+1;
		char tmp=S->ch[i];
		S->ch[i]=S->ch[j];
		S->ch[j]=tmp;
	}	
}

//4.(1)③
//删除所有ch 
void charDelete(SString *S,char ch){
	char chars[S->len];
	int c=1;
	int i;
	for (i=1;i<=S->len;i++){
		if(S->ch[i]!=ch){
			chars[c++]=S->ch[i]; 
		}
	}	
	for (i=1;i<=c;i++){
		S->ch[i]=chars[i];
	}
	S->len=c;
}

int Index(SString S,int pos,SString T){
	int i=pos,j=1;//主串从第pos开始,模式串从头开始
	while (i<=S.len&&j<=T.len){
		if(S.ch[i]==T.ch[j]){//当对应字符相等时,比较后续字符
			i++;
			j++;
		}
		else{				//当对应字符不等时
			i=i-j+2;			//主串回溯到j-j+2的位置重新比较
			j=1;				//模式串从头开始重新比较
		}
	}
	if(j>T.len)	return i-T.len;	//匹配成功时,返回匹配起始位置
	else return 0;				//匹配失败时,返回0
}

//4.(1)④ 
//查找子串
//调用BF算法 
int StringIndex(SString *S1,int index,SString *S2){	
	return Index(*S1,index,*S2);
}

int main(){
	SString S;

	char *chars="abcabc";
	printf("建立串S\n"); 
	StrAssign(&S,chars);
	
	printf("输出串S\n");
	Output(&S);

	char ch='a';
	char ch1='b';
	char ch2='d';
	printf("将ch1(%c)替换为ch2(%c)\n",ch1,ch2); 
	charReplace(&S,ch1,ch2);
	Output(&S);
	
	printf("将S翻转\n",ch1,ch2); 
	StringReserve(&S);
	Output(&S);	
	
	printf("将S删除ch(%c)\n",ch); 
	charDelete(&S,ch);
	Output(&S);	
	
	SString T;
	char *chars2="dc";		
	StrAssign(&T,chars2);
	
	printf("输出串T\n");
	Output(&T);	 
	
	int ix=StringIndex(&S,1,&T);
	printf("%d\n",ix);
	
} 

4(3)编写算法,实现顺序串的基本操作 StrReplace(S,T,V)

最后

2023-11-3 19:01:45

我们都有光明的未来
不必感谢我，也不必记得我

祝大家考研上岸
祝大家工作顺利
祝大家得偿所愿
祝大家如愿以偿
点赞收藏关注哦