AVLTree代码刨析
AVLTree原理:
AVLTree是高度平衡二叉树,每一个节点的左右子树高度差都小于2,这是AVLTree高度平衡的由来,他是在平衡二叉树的基础上进行特殊的处理(旋转:如果该节点不满足高度平衡二叉树的特点就进行旋转 旋转目的是为了调整该节点左右子树高度差 促使其达到高度平衡二叉树)
AVLTree节点之间是通过三叉链(里面存有三个节点:_parent,_left,_right)进行链接的 这样做为了更好的用迭代器去遍历二叉树
AVLTree缺点也很明显,旋转次数太多,但红黑树旋转就较少,所以AVLTree树的建立较耗时间,红黑树肯会更优。
补充:AVLTree就是为了更好的搜索查找而设计的,根据树的特点,深度越深所存的值就越多,查找也就越快,所以说该树主要为查找而生,实现删除功能会逆着之前的步骤进行调整,所以没有实现。我感觉重建二叉树也不会太费时间。
平衡原理:
该篇AVLTree是通过平衡因子(balance fact)进行调整;
平衡因子取值:0,1/-1,2/-2;
通过左树新增节点父亲的平衡因子“--” 右树新增节点父亲的平衡因子“++”
当父亲的平衡因子为2/-2时;说明左右子树高度差已经等于2了,不满足高度平衡二叉树,此时就要进行相应的旋转,如何进行旋转待会再细说。
当父亲的平衡因子为1/-1时;继续向上更新,因为以该节点为根的树,还是高度平衡二叉树,但是不保证新增的节点对他的祖先不产生影响,有可能他的祖先平衡因子会变成2/-2,这样就会发生上述的旋转,所以要进行向上更新。
平衡二叉树的主要难点就是旋转 旋转搞清楚就没什么困难了。
平衡二叉树的旋转:
之前就提到过旋转是调整以该节点,为旋转轴的子树的高度,所以说旋转之后该树已经是平衡二叉树了,所以不用再向上更新平衡因子。平衡因子会在每次旋转之后进行更新。
注意:AVLTree旋转使创始者规定的,这样做肯定是更好的,所以不要产生疑问,如为什么要这样旋转,为什么不是那样旋转?必须遵循AVLTree的旋转规则,一步一步画图去走。
我的建议:看懂以后,需要反复去练习,这里面运用的知识还是挺多的,如树,平衡二叉树,节点之间的链接(与链表链接十分相似),大大提高知识的运用与理解。
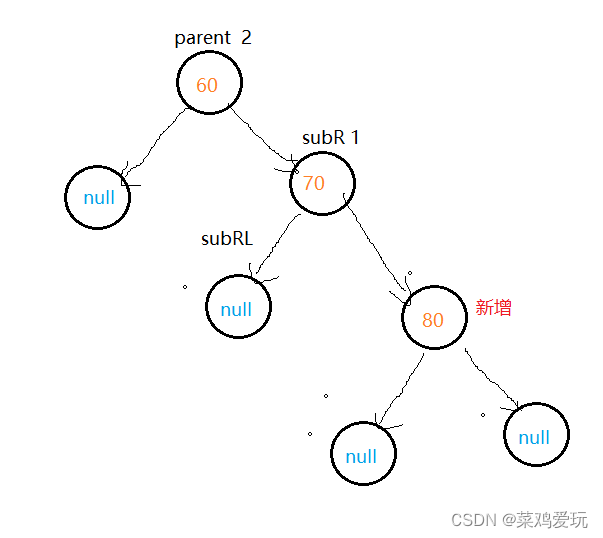
右旋:
右旋示例图:
右边高了,必须使右边降下来,构成平衡二叉树,旋转过程如下图:
代码如下:
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//建立parent与subRL之间的关系
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//建立parent与subR之间的关系
Node* ppNode = parent->_parent;
parent->_parent = subR;
subR->_left = parent;
if (ppNode == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
subR->bf = parent->bf = 0;//平衡因子的更新
}平衡因子更新如上图所示,根据旋转之后的图,调整平衡因子。
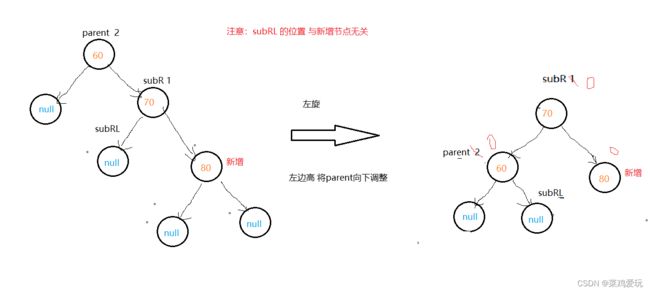
左旋:
左旋示例图:
左边高了,必须使左边降下来,构成平衡二叉树,旋转过程如下图:
代码如下:
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (ppNode == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
subL->bf = parent->bf = 0;
}平衡因子更新如上图所示,根据旋转之后的图,调整平衡因子。
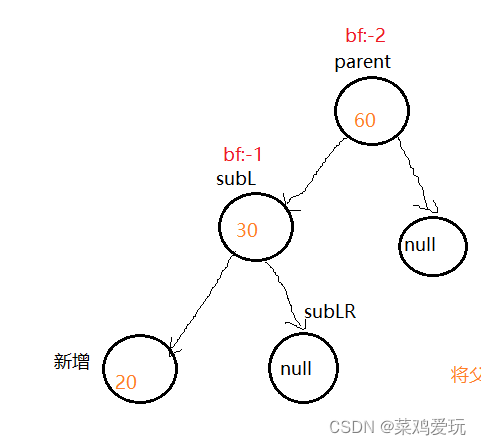
左右旋:
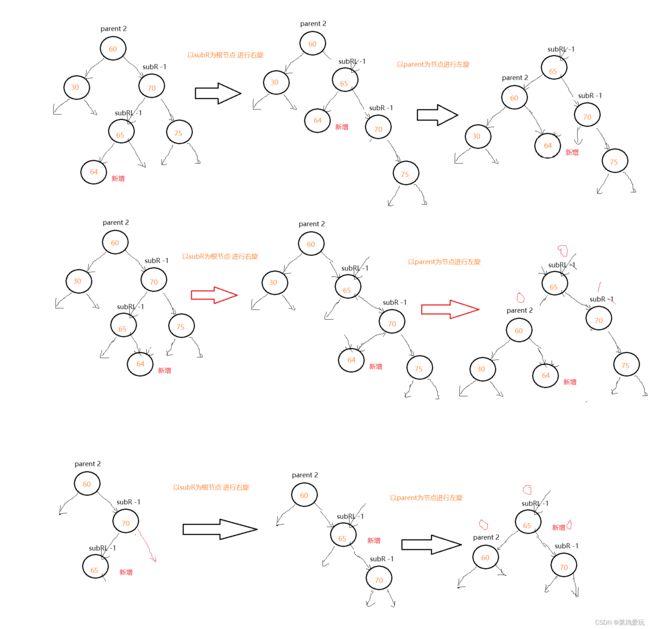
该新增节点使根节点的左右子树不能构成平衡二叉树,需要进行旋转调整高度差,旋转过程如下图:
没有更新旋转过程的平衡因子,但是每个旋转函数中,都会对平衡因子进行更新,只是我没有在图上更新,旋转最终平衡因子可以根据图去更新
上面三种图,对应代码中三种情况的平衡因子更新,可能顺序有点乱。
代码如下:
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->bf;
RotateL(subL);//左旋
RotateR(parent);//右旋
if (bf == -1)//左子树新增
{
subLR->bf = 0;
subL->bf = 0;
parent->bf = 1;
}
else if (bf == 1)//右子树新增
{
subLR->bf = 0;
subL->bf = -1;
parent->bf = 0;
}
else if (bf == 0)//本身就是新增
{
subLR->bf = 0;
subL->bf = 0;
parent->bf = 0;
}
else
{
assert(false);
}
}右左旋:
该新增节点使根节点的左右子树不能构成平衡二叉树,需要进行旋转调整高度差,旋转过程如下图:
没有更新旋转过程的平衡因子,但是每个旋转函数中,都会对平衡因子进行更新,只是我没有在图上更新,旋转最终平衡因子可以根据图去更新
上面三种图,对应代码中三种情况的平衡因子更新,可能顺序有点乱。
代码如下:
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->bf;
RotateR(subR);//右旋
RotateL(parent);//左旋
if (bf == -1)//左子树新增
{
subRL->bf = 0;
subR->bf = 1;
parent->bf = 0;
}
else if (bf == 1)//右子树新增
{
subRL->bf = 0;
subR->bf = 0;
parent->bf = -1;
}
else if(bf == 0)//本身是新增
{
subRL->bf = 0;
subR->bf = 0;
parent->bf = 0;
}
else
{
assert(false);
}
}以上是平衡二叉树的旋转代码实现,如果不对请指教,
平衡二叉树的遍历:
平衡二叉树的遍历采用中序遍历,原因是平衡二叉树左子树始终小于根节点,根节点始终小于右子树,而中序遍历正好是:左,中,右,正好是升序遍历所以采用中序遍历
void Inorder()
{
_Inorder(_root);
}
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_Inorder(root->_right);
}平衡二叉树的判断:
平衡二叉树:左右子树高度差不超过1。
LCR 175. 计算二叉树的深度
平衡因子:就是右子树高度减左子树高度,其差值(可正负)就是平衡因子。
LCR 176. 判断是否为平衡二叉树
同时上面两个条件也可以做两个题。
int Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
int lh = Height(root->_left);
int rh = Height(root->_right);
return lh > rh ? lh + 1 : rh + 1;
}
bool IsBalance()
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int lh = Height(root->_left);
int rh = Height(root->_right);
if (rh - lh != root->bf)
{
cout << "平衡因子异常" << endl;
return false;
}
return abs(rh - lh) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}以上是通过平衡因子进行判断旋转,有的可能是通过计算该节点左右子树的高度差进行旋转,道理是一样的,平衡因子就是右子树高度减左子树高度得到的值(可正负)。
完整代码:
#pragma once
#include
using namespace std;
#include
#include
#include
template
struct AVLTreeNode
{
pair _kv;
AVLTreeNode* _parent;
AVLTreeNode* _left;
AVLTreeNode* _right;
int bf;//blance fact 平衡因子
AVLTreeNode(const pair& kv)
:_kv(kv)
,_parent(nullptr)
,_left(nullptr)
,_right(nullptr)
,bf(0)
{}
};
template
class AVLTree
{
typedef AVLTreeNode Node;
private:
Node* _root = nullptr;
public:
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
//向下寻找该节点该去的位置
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;//已经存在
}
}
//parent就是要插入节点的父亲 判断该节点是左孩子还是右孩子
cur = new Node(kv);
if (parent->_kv.first > cur->_kv.first)
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}//不存在相等的情况
while (parent)
{
//左子树新增--
//右子树新增++
if (parent->_left == cur)
{
parent->bf--;
}
else
{
parent->bf++;
}
//如果parent->bf==0就不再继续更新 因为左右子树已经平衡
//如果parent->bf==1/-1还要继续往上更新 因为左右子树不平衡
//如果parent->bf==2/-2就要旋转 因为已经出现左右子树的高度差不等于1 不是搜索树
if (parent->bf == 0)
{
break;
}
else if (parent->bf == 1 || parent->bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if(parent->bf==2||parent->bf==-2)
{
if (parent->bf == 2 && cur->bf == 1)
{
RotateL(parent);
}
else if (parent->bf == -2 && cur->bf == -1)
{
RotateR(parent);
}
else if (parent->bf == 2 && cur->bf == -1)
{
RotateRL(parent);
}
else if (parent->bf == -2 && cur->bf == 1)
{
RotateLR(parent);
}
else
{
assert(false);
}
break;//旋转之后以该节点为根节点的树已经平衡 旋转目的就是为了平衡左右子树
}
}
return true;
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//建立parent与subRL之间的关系
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//建立parent与subR之间的关系
Node* ppNode = parent->_parent;
parent->_parent = subR;
subR->_left = parent;
if (ppNode == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
subR->bf = parent->bf = 0;//平衡因子的更新
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (ppNode == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
subL->bf = parent->bf = 0;
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->bf;
RotateL(subL);
RotateR(parent);
if (bf == -1)//左子树新增
{
subLR->bf = 0;
subL->bf = 0;
parent->bf = 1;
}
else if (bf == 1)//右子树新增
{
subLR->bf = 0;
subL->bf = -1;
parent->bf = 0;
}
else if (bf == 0)//本身就是新增
{
subLR->bf = 0;
subL->bf = 0;
parent->bf = 0;
}
else
{
assert(false);
}
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->bf;
RotateR(subR);
RotateL(parent);
if (bf == -1)
{
subRL->bf = 0;
subR->bf = 1;
parent->bf = 0;
}
else if (bf == 1)
{
subRL->bf = 0;
subR->bf = 0;
parent->bf = -1;
}
else if(bf == 0)
{
subRL->bf = 0;
subR->bf = 0;
parent->bf = 0;
}
else
{
assert(false);
}
}
void Inorder()
{
_Inorder(_root);
}
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_Inorder(root->_right);
}
int Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
int lh = Height(root->_left);
int rh = Height(root->_right);
return lh > rh ? lh + 1 : rh + 1;
}
bool IsBalance()
{
return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int lh = Height(root->_left);
int rh = Height(root->_right);
if (rh - lh != root->bf)
{
cout << "平衡因子异常" << endl;
return false;
}
return abs(rh - lh) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
};
void TestAVLTree1()
{
//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree t;
for (auto e : a)
{
t.Insert(make_pair(e, e));
}
t.Inorder();
cout << t.IsBalance() << endl;
}
void TestAVLTree2()
{
srand(time(0));
const size_t N = 100000;
AVLTree t;
for (size_t i = 0; i < N; ++i)
{
size_t x = rand();
t.Insert(make_pair(x, x));
//cout << t.IsBalance() << endl;
}
//t.Inorder();
cout << t.IsBalance() << endl;
} 以上就是AVLTree的重要内容,有什么疑惑或者文章错误请指教~
下期发布红黑树讲解