<<算法很美>>——(五)——回溯算法核心框架(上)
目录
前言
基本概念
基本框架
例题:全排列
前言
本篇博客来自回溯算法解题套路框架 :: labuladong的算法小抄 (gitee.io),想在此做个学习笔记和大家共同学习,加深印象.
视频版:【labuladong】回溯算法核心套路详解_哔哩哔哩_bilibili
基本概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称
基本框架
1.回溯算法就是一种暴力穷举法
2.穷举过程其实就是遍历一棵多叉树的过程.
3.回溯算法的代码框架和多叉树遍历代码框架相似
站在回溯的某个节点上,我们需要思考三个问题:
- 路径:就是我们当前做出的选择
- 选择列表:就是我们当前可以做出的选择
- 结束条件:也就是到达决策树底部,无法再做出选择
框架:
result=[];
def backtrack(路径,选择列表)
if 满足结束条件:
result.add(路径);
return
for 选择 in 选择列表
做选择
backtrack(路径,选择列表)
撤销选择
上面代码的核心的部分就是for循环里面的做出选择,然后进行递归,之后进行撤销选择.可能到这里还是对上面的三个问题很懵,不太懂,没关系,不用慌,这里只是提一下,留点印象即可,下面我会跟大家一起做全排列和N皇后两个经典题目,对其进行深度剖析。
例题:全排列
拿到这个问题我们会怎么思考囊?首先我们举个{1,2,3}这个例子,我们一般会固定一个数1,然后第二位可以拿2,最后一位拿3,也可以第二位拿3,最后一位拿2。然后再按这样穷举后两位...
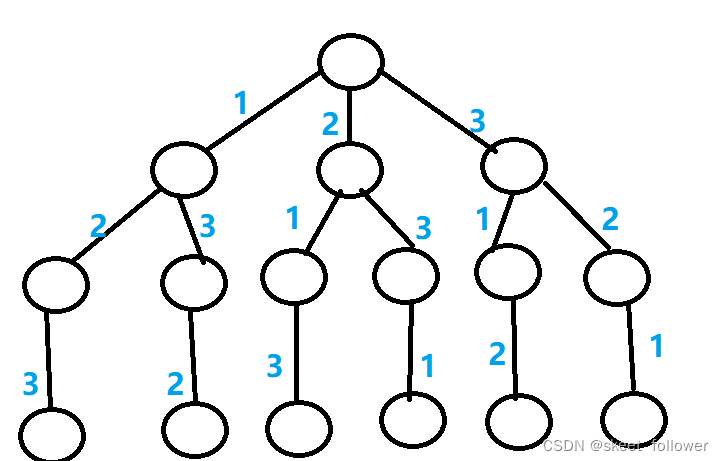
这样听起来感觉很懵,因此我们画个回溯树帮助我们理解
按照这个回溯树依次从根开始遍历,其实就是所有的全排列。我们不妨称为这棵回溯树为决策树。为什么这么说囊,就是我们站在每个节点都要去决策下一步往哪走,看图,假如我们站在1下。
我们现在可以选择2或者3,为什么不能选择1囊,因为我们前面已经走过了,而全排列又不允许重复.
1就是路径,记录我们已经走过的路径.2和3就是选择列表,表示我们当前可以选择的路径。结束条件就是遍历到树的底层叶子结点为空,选择列表为空时。
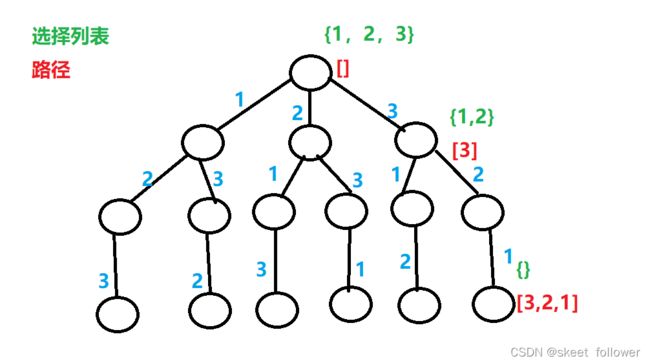 我们定义的
我们定义的 backtrack 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
实都是树的遍历问题,而多叉树的遍历框架就是这样:
void traverse(TreeNode root) {
for (TreeNode child : root.childern) {
// 前序遍历需要的操作
traverse(child);
// 后序遍历需要的操作
}
}
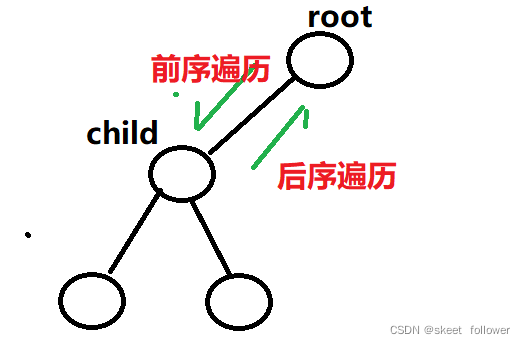
而所谓的前序遍历和后序遍历,只是在两个不同时间点做的事.前序遍历是在进入某个节点之前那个时间点遍历,后序遍历是在进入某个节点之后那个时间点遍历。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确维护节点的属性,那么就要在这两个特殊时间点搞点动作:
现在是否理解回溯的核心框架
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
代码:
List> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
List> permute(int[] nums) {
// 记录「路径」
LinkedList track = new LinkedList<>();
// 「路径」中的元素会被标记为 true,避免重复使用
boolean[] used = new boolean[nums.length];
backtrack(nums, track, used);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素(used[i] 为 false)
// 结束条件:nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList track, boolean[] used) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (used[i]) {
// nums[i] 已经在 track 中,跳过
continue;
}
// 做选择
track.add(nums[i]);
used[i] = true;
// 进入下一层决策树
backtrack(nums, track, used);
// 取消选择
track.removeLast();
used[i] = false;
}
}
在蓝桥杯天梯赛中我们更经常看到的是下面这个形式的代码
#include
#include
#include
using namespace std;
int ants ;
int a[10] = { 0,1,2,3,4,5,6,7,8,9 };
void f(int k)
{
if (k == 10)
{
//这里一般还会有个判断条件
return;
}
//从k位开始的每个字符,都尝试放在K这个位置
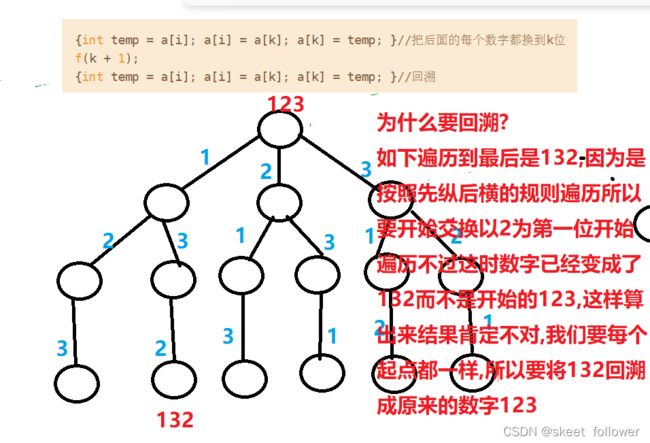
for (int i = k; i < 10; i++)
{
{int temp = a[i]; a[i] = a[k]; a[k] = temp; }//把后面的每个数字都换到k位
f(k + 1);
{int temp = a[i]; a[i] = a[k]; a[k] = temp; }//回溯
}
}
int main()
{
f(0);
cout << ants << endl;
return 0;
} 学过C++的朋友都知道可以直接用next_permutation实现
#include
#include
#include
using namespace std;
int ants;
int a[10] = { 0,1,2,3,4,5,6,7,8,9 };
int main()
{
do {
ants++;
} while (next_permutation(a, a + 10));
//f(0);
cout << ants << endl;
return 0;
} 当然也可以这道题也可以用前缀和,迭代等方法做,感兴趣的伙伴们可以下去尝试一下。至此我们回溯算法的框架就介绍完了,下一篇我们进行N皇后的求解。