二叉树的实现及其遍历
递归搞得我怀疑人生,写个二叉树缓解一下心情......
满二叉树:
包含2^k-1个节点
每层的节点数为2^(k-1)
完全二叉树:
除了最后一层所有层的节点都是满的
具有n个节点的完全二叉树的深度为log2n+1
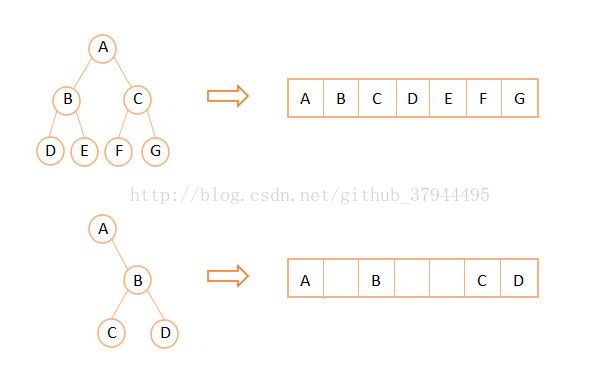
1、二叉树的顺序存储
使用数组来记录二叉树的所有节点,存储情况如下图所示:
代码如下:
class ArrayBinTree {
//使用数组来记录该树的所有节点
private Object[] datas;
private int DEFAULT_DEEP = 8;
//保存该树的深度
private int deep;
private int arraySize;
//以默认的深度来创建二叉树
public ArrayBinTree() {
this.deep = DEFAULT_DEEP;
this.arraySize = (int) Math.pow(2, deep) - 1;//二叉树总节点的个数,是个公司
datas = new Object[arraySize];
}
//以指定深度来创建二叉树
public ArrayBinTree(int deep) {
this.deep = deep;
this.arraySize = (int) Math.pow(2, deep) - 1;
datas = new Object[arraySize];
}
//以指定深度,指定根节点创建二叉树
public ArrayBinTree(int deep, T data) {
this.deep = deep;
this.arraySize = (int) Math.pow(2, deep) - 1;
datas = new Object[arraySize];
datas[0] = data;
}
/**
* 为指定节点添加子节点。
* @param index 需要添加子节点的父节点的索引
* @param data 新子节点的数据
* @param left 是否为左节点
*/
public void add(int index , T data , boolean left){
if (datas[index] == null){
throw new RuntimeException(index + "处节点为空,无法添加子节点");
}
if (2 * index + 1 >= arraySize){
throw new RuntimeException("树底层的数组已满,树越界异常");
}
//添加某个指定index的左子节点,奇数
if (left){
datas[2 * index + 1] = data;
}else{//偶数 添加某个指定index的右子节点,奇数
datas[2 * index + 2] = data;
}
}
//判断二叉树是否为空。
public boolean empty(){
//根据根元素来判断二叉树是否为空
return datas[0] == null;
}
//返回根节点。
public T root(){
return (T)datas[0] ;
}
//返回指定节点(非根节点)的父节点。
public T parent(int index){
return (T)datas[(index - 1) / 2] ;//整除,不会产生小数,生成节点的逆向
}
//返回指定节点(非叶子节点)的左子节点。当左子节点不存在时返回null
public T left(int index){
if (2 * index + 1 >= arraySize){
throw new RuntimeException("该节点为叶子节点,无子节点");
}
return (T)datas[index * 2 + 1] ;
}
//返回指定节点(非叶子节点)的右子节点。当右子节点不存在时返回null
public T right(int index){
if (2 * index + 2 >= arraySize){
throw new RuntimeException("该节点为叶子节点,无子节点");
}
return (T)datas[index * 2 + 2] ;
}
//返回该二叉树的深度。
public int deep(int index){
return deep;
}
//返回指定节点的位置。
public int pos(T data){
//该循环实际上就是按广度遍历来搜索每个节点
for (int i = 0 ; i < arraySize ; i++){
if (datas[i].equals(data)){
return i;
}
}
return -1;
}
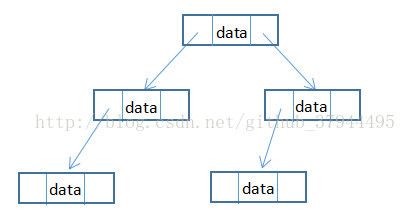
} 为每个节点增加左右两个指针,分别指向该节点的左右两个子节点
(刚才不知道点了什么,屏幕中突然出现了一条提示“ALT+左箭头可后退”,在我还没有理解这句话的时候我的手已经做出了反应,alt+左箭头毫不犹豫的按了下去,结果......真的后退了......我之前打的字粘的代码传的图片都没有了......如果你想清空刚才你写的文章的话这不失为一个好方法,要不然朋友们还是不要轻易尝试了......)
链表存储情况如下图所示:
代码如下:
class LinkBinTree {
public static class TreeNode{
Object data;
TreeNode left;
TreeNode right;
public TreeNode(){
}
public TreeNode(Object data){
this.data = data;
}
public TreeNode(Object data , TreeNode left, TreeNode right){
this.data = data;
this.left = left;
this.right = right;
}
}
private TreeNode root;
//以默认的构造器来创建二叉树
public LinkBinTree(){
this.root = new TreeNode();
}
//以指定根元素来创建二叉树
public LinkBinTree(E data){
this.root = new TreeNode(data);
}
/**
* 为指定节点添加子节点。
* @param parent 父节点
* @param data 新子节点的数据
* @param isLeft 是否为左节点
* @return 新增的节点
*/
public TreeNode addNode(TreeNode parent , E data, boolean isLeft){
if (parent == null) {//父亲为空
throw new RuntimeException(parent +
"节点为null,无法添加子节点");
}
if (isLeft && parent.left != null){//已经有左节点了
throw new RuntimeException(parent +
"节点已有左子节点,无法添加左子节点");
}
if (!isLeft && parent.right != null){//已经有右节点了
throw new RuntimeException(parent +
"节点已有右子节点,无法添加右子节点");
}
TreeNode newNode = new TreeNode(data);
if (isLeft) {
//让父节点的left引用指向新节点
parent.left = newNode;
}else{
//让父节点的left引用指向新节点
parent.right = newNode;
}
return newNode;
}
//判断二叉树是否为空。
public boolean empty(){
//根据根元素来判断二叉树是否为空
return root.data == null;
}
//返回根节点。
public TreeNode root(){
if (empty()){
throw new RuntimeException("树为空,无法访问根节点");
}
return root;
}
//返回指定节点(非叶子)的左子节点。当左子节点不存在时返回null
public E leftChild(TreeNode parent){
if (parent == null){
throw new RuntimeException(parent +
"节点为null,无法添加子节点");
}
return parent.left == null ? null : (E)parent.left.data;
}
//返回指定节点(非叶子)的右子节点。当右子节点不存在时返回null
public E rightChild(TreeNode parent){
if (parent == null) {
throw new RuntimeException(parent +
"节点为null,无法添加子节点");
}
return parent.right == null ? null : (E)parent.right.data;
}
//返回该二叉树的深度。
public int deep(){
//获取该树的深度
return deep(root);
}
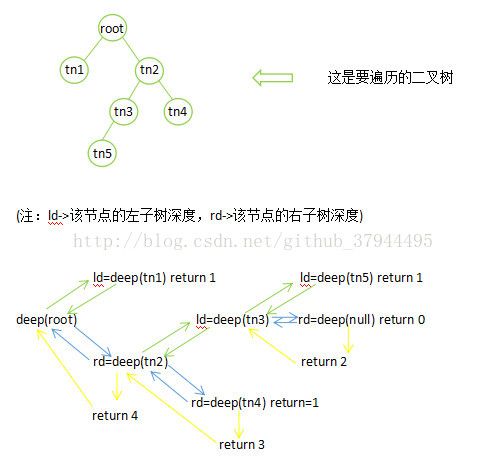
//这是一个递归方法:每棵子树的深度为其所有子树的最大深度 + 1
private int deep(TreeNode node){
if (node == null){
return 0;
}
//没有子树
if (node.left == null && node.right == null){
return 1;
}else{
int leftDeep = deep(node.left);
int rightDeep = deep(node.right);
//记录其所有左、右子树中较大的深度
int max = leftDeep > rightDeep ? leftDeep : rightDeep;
//返回其左右子树中较大的深度 + 1
return max + 1;
}
}
} (终于弄明白了最后一个计算深度的递归方法,画个图庆祝一下......)
3、二叉树的先序、中序、后序遍历
先序(DLR):
(1)访问根节点
(2)先序遍历左子树
(3)先序遍历右子树
中序(LDR):
(1)中序遍历左子树
(2)访问根节点
(3)中序遍历右子树
后序(LRD):
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根节点
public class Traverse {
class TreeNode{
private T data;
private TreeNode leftNode;
private TreeNode rightNode;
public TreeNode(T data,TreeNode leftNode,TreeNode rightNode){
this.data=data;
this.leftNode=leftNode;
this.rightNode=rightNode;
}
public T getData(){
return data;
}
public void setData(T data){
}
public TreeNode getLeftNode(){
return leftNode;
}
public void setLeftNode(TreeNode leftNode){
this.leftNode=leftNode;
}
public TreeNode getRightNode(){
return rightNode;
}
public void setRightNode(TreeNode rightNode){
this.rightNode=rightNode;
}
}
public TreeNode init(){
TreeNode D=new TreeNode("D",null,null);
TreeNode H=new TreeNode("H",null,null);
TreeNode I=new TreeNode("I",null,null);
TreeNode J=new TreeNode("J",null,null);
TreeNode P=new TreeNode("K",null,null);
TreeNode G=new TreeNode("G",P,null);
TreeNode F=new TreeNode("F",null,J);
TreeNode E=new TreeNode("E",H,I);
TreeNode B=new TreeNode("B",D,E);
TreeNode C=new TreeNode("C",F,G);
TreeNode A=new TreeNode("A",B,C);
return A;
}
public void printNode(TreeNode node){
System.out.println(node.getData()+" ");;
}
//先序遍历
public void pre_order(TreeNode node){
this.printNode(node);//D
if(node.getLeftNode()!=null){//L
this.pre_order(node.getLeftNode());
}
if(node.getRightNode()!=null){
this.pre_order (node.getRightNode());
}
}
//中序遍历
public void in_order(TreeNode node){
if(node.getLeftNode()!=null){//L
this.in_order(node.getLeftNode());
}
this.printNode(node);//D
if(node.getRightNode()!=null){//R
this.in_order(node.getRightNode());
}
}
//后序遍历
public void post_order(TreeNode node){
if(node.getLeftNode()!=null){//L
this.post_order(node.getLeftNode());
}
if(node.getRightNode()!=null){//R
this.post_order(node.getRightNode());
}
this.printNode(node);//D
}
public static void main(String[] args) {
Traverse Tree=new Traverse();
TreeNode node=Tree.init();
System.out.println("先序遍历DLR的情况");
Tree.pre_order(node);
System.out.println("中序LDR遍历的情况");
Tree.in_order(node);
System.out.println("后序遍历LRD的情况");
Tree.post_order(node);
}
}
实现代码如下:
public void level(TreeNode node){
Queue> queue=new ArrayDeque>();
queue.add(node);
while(!queue.isEmpty()){
TreeNode n=queue.poll();
this.printNode(n);
if(n.getLeftNode()!=null){
queue.add(n.getLeftNode());
}
if(n.getRightNode()!=null){
queue.add(n.getRightNode());
}
}
}