11.2需求曲线，消费者剩余，成本函数，需求函数

劳动的边际产量就是说单增加劳动要素，会增加多少的Q，是在Q为一定值的情况下，每个具体情况下的投资效益

平均产量函数是说已投入的L，每个L平均会增加多少产量

边际技术替代率是说，K与L之间的替代率，在每个具体Q的情况下

那就是得到由生产函数得到K与Q和L之间的关系，然后对L求偏导，就可以得到替代率函数

问增减性，就接着求导

劳动的边际产量函数的增减性，边际产量函数对劳动要素求导

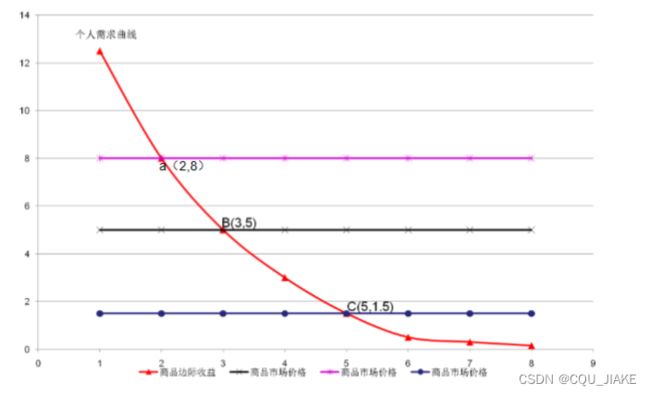
需求曲线

需求函数刻画的是需求与价格之间的关系式，从消费者角度理解是，如果价格是多少，那么会购买多少，即需求多少，注意，是一定会买的数量，多的不买，少的不够，在这个价位下

从厂商的角度理解就反过来了，即如果只想要他买一件，那么最高可以定价多高，即可以定价很高，但是消费者只会买一件，而且是一定会买一件，如果定价再高，消费者就不会购买，

就是因为此时，消费者的支付意愿已经低于了市场定价，就不会再购买

如果定价低一点，消费者此时消费意愿大于市场定价，就会产生此时的消费者剩余，

也就是说，个人需求曲线上的点，是消费者在当下价格下所能接受的购买商品的最大数量，但是它买的数量不一定就是这个数量，是介于0~这个曲线之间的，但是一定不会超过它

还没到边界时，说明还有边际收益，再买，则边际收益降低

边际收益曲线就是消费者商品需求曲线理解就是，轴的含义反转一下，

假定一个定价，就会得到这个定价下，消费者愿意购买的最大数量，之所以不继续购买，是因为此时边界上的点，就是满足边际收益=边际成本，边际成本始终是此时的定价，那就是说明，曲线上的点，两个坐标，一个是消费者需求量，也即所谓最大购买量，一个是此时定价，但是此时定价=边际成本=边际收益，所以也可以理解为需求量与边际收益的关系

产生消费者剩余，也可以理解为，消费者还没买到当下定价下所能购买到的最大数量，即消费者肯定还乐意继续购买，但是还没有购买，所以就产生了剩余。

如果消费者想买的数量越多，那么它所能接受的每件单价的最高定价也就越低；反着理解就是，如果定价越低，那么消费者愿意购买的最大数量就越多。

定价一定时，肯定对应着一个最大的意愿购买数量，此时，边际收益恰好等于定价

但是之前的时候，即还没买到最大意愿购买数量时，消费者肯定是非常乐意购买的，因为第一件的时候，第一件的边际收益远远大于不变的定价，随着买的数量不断增加，边际收益与不变的定价之间的差值越来越小，直到到需求曲线上的相等

横轴是商品价格，纵轴是需求数量；价格越高，需求越是少。

对于商品边际收益，横轴是生产数量，纵轴是边际收益，生产越多，边际收益越小

需求与市场价之间的关系，一般市场价越高，需求越少；越低，需求越高。

消费者购买商品的边际收益曲线就是消费者的商品需求曲线

价格越高，需求越低，买的越少；买的少，则边际收益高

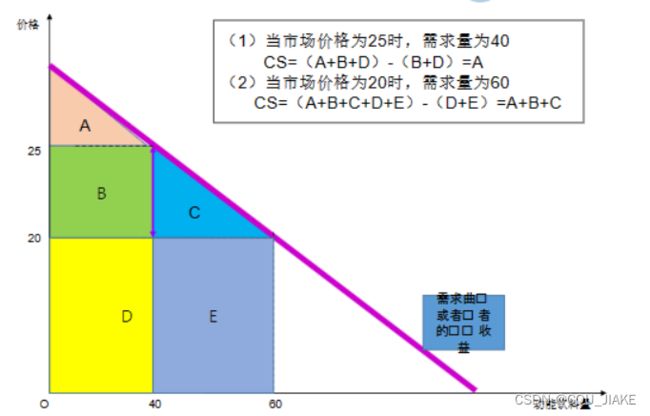
消费者剩余

消费者为一定量的某种商品愿意支付的价格和他实际支付的价格之间可能出现差额，

一方面，由于存在边际效用递减规律，随着消费者购买数量的增多，愿意支付的价格越来越低。

越来越低的价格是由于边际效用递减的因素影响，即买的越多，实际的收益越低

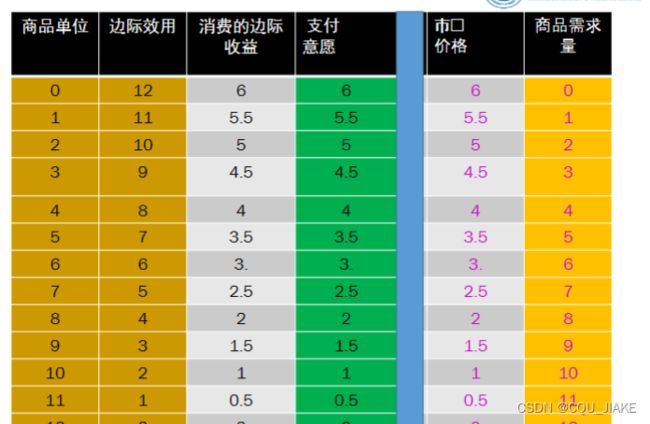
支付意愿等于消费者的边际收益，就是说当下购买商品的收益，即边际收益越大，那么支付意愿越大，，反之，则越小。当支付意愿高于市场价格的商品单位时，就会购买；不然，支付意愿低迷时，就不会购买。说的就是边际收益和市场价格之间的一个关系

已知个人需求曲线，就是需求与价格之间的一个关系，要求边际收益曲线，就是价格

消费者个人需求曲线不仅是消费者的边际收益曲线，而且也是消费者支付意愿曲线

消费者剩余：消费者的需求价格与市场价格之间的差额

边际剩余=边际支付意愿-市场单价

最高定价不应该超过边际支付意愿，不然就不会购买，即分布在费用与边际支付意愿之间

消费者的总剩余=支付意愿总额-市场价格总额=消费者总收益-消费者购买总支出

支付意愿总额

需求曲线是需求量与价格之间的关系。边际收益曲线是数量与边际收益之间的关系，

数量越多，边际收益越小；从需求曲线上看，是需求量越多，则反映的是价格越小

理解的话，就不是一个单纯的量增量减的，而是二元的，二者相互影响，只不过画出来是一个东西

要确定消费者剩余，价格与需求量二者缺一不可

成本函数

成本函数是指在目标产量Q给定下，怎样调整各要素投入量，从而使购买各要素服务的总支出最小化，就是最小成本与产量Q的关系式，并可以确定出各要素投入量的一个具体情况

此时最小化的支出与产量Q的关系就是成本函数

然后成本函数是要通过其，由当下的生产要素情况以及给定的Q，得到当下的一个最小生产成本

生产函数

生产函数，在一定时期内，技术水平不变的情况下，生产中所用的各种生产要素的数量与所能生产的最大产量之间的关系。就是通过生产函数，可以由当下的生产要素情况得到当下的最大产量

生产函数的因变量是最大产量，就是Q，自变量是各种生产要素，如Q=f(K,L)就是说根据当下的K,L得到当下的最大产量，即Q

由生产函数得到成本函数

思路是，在给定生产函数和要素价格的条件下，通过拉格朗日乘数法求出“在既定产量下”的成本最小化的原则

再通过成本最小化原则，将其中一种要素数量改写成另一种要素数量的关系式，带入生产函数

目标函数是总成本，让其最小化。限制条件是生产函数

其最小化时，对各生产要素的偏导为0，