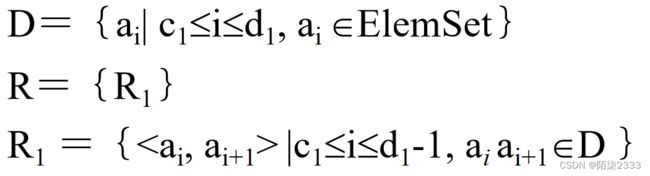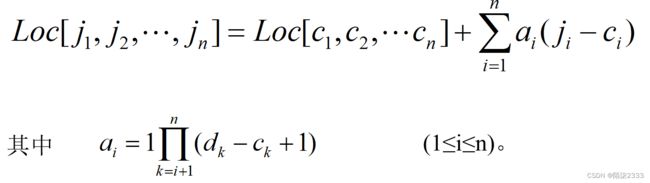数据结构（超详细讲解！！）第二十节 数组

1.定义

1.概念

相同类型的数据元素的集合。    

记作：A=(A0,A1,…,Am-1)

二维数组可看作是每个数据元素都是相同类型的一维数组的一维数组。多维数组依此类推。

二维数组是数据元素为线性表的线性表。

A=(A0，A1，……，An-1)

其中：  Ai=(ai0，ai1，……，ai m-1)         (0≤i≤n-1)

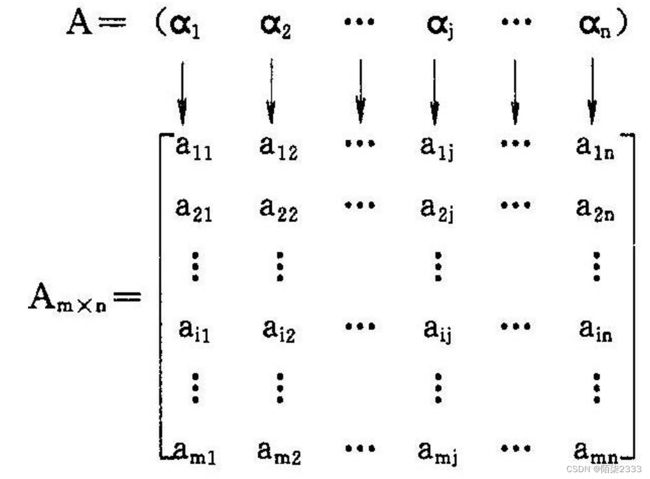
 Am×n的二维数组

矩阵Am×n看成n个列向量的线性表

矩阵Am×n看成m个行向量的线性表

 以上我们以二维数组为例介绍了数组的结构特性，实际上数组是一组有固定个数的元素的集合。

 也就是说，一旦定义了数组的维数和每一维的上下限，数组中元素的个数就固定了。      

例如二维数组A3×4，它有3行、4列，即由12个元素组成。

由于这个性质，使得对数组的操作不像对线性表的操作那样可以在表中任意一个合法的位置插入或删除一个元素。      

对于数组的操作一般只有两类：                        

(1) 获得特定位置的元素值；                        

(2) 修改特定位置的元素值。

2.数组的逻辑结构定义

数组的逻辑结构定义：ARRAY=(D, R)

其中D是数据元素的集合，R是描述下标的关系的集合

由此，对于一维数组有：

c1 ，d1为一维数组下标的下界和上界。

二维数组：

n维数组：

逻辑特性：

3.数组的抽象类型定义：

基本操作：

基本操作：
   InitArray(&A,n,bound1,…,boundn)
          操作结果：若维数n和各维长度合法，则构造相应的数组A，并返回OK。
    DestroyArray(&A)
          操作结果：销毁数组A。
    Value(A,&e,index1,…,indexn)
          初始条件：A 是n维数组，e为元素变量，随后是n个下标值。
              操作结果：若各下标不越界，则e赋值为所指定的A的元素值，并返回OK。
    Assign(&A,e,index1,…,indexn)
          初始条件：A是n维数组，e为元素变量，随后是n个下标值。
              操作结果：若下标不越界，则将e的值赋值给所指定的A的元素，并返回OK。
}//ADT Array

2.数组的顺序表示和实现

由于数组的运算一般不包括插入和删除，因此不必考虑数据元素的移动。因而采用顺序存储方式是较为适宜的。

（1）行主次序存取，即把二维数组看成行向量组成的一维结构。

此方式下的存储映象为：行主次序

（2）列主次序存取，即把二维数组看成列向量   组成的一维结构。

此方式下的存储映象为：列主次序

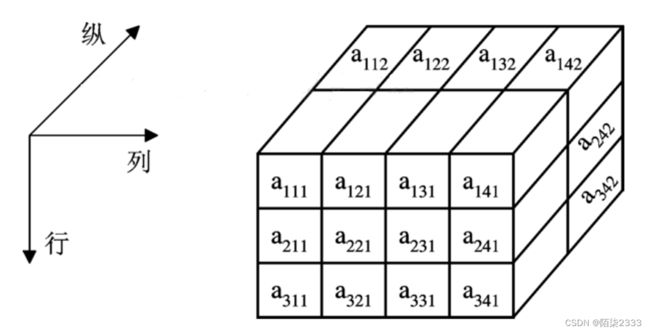
假设有一个3×4×2的三维数组A ，共有24个元素，其逻辑结构如图所示。

 三维数组元素的标号由三个数字表示，即行、列、纵三个方向。

a142表示第1行，第4列，第2纵的元素。

如果对A3×4×2（下标从1开始）采用以行为主序的方法存放，即行下标变化最慢，纵下标变化最快，则顺序为：

       a111，a112，a121，a122， …，a331，a332，a341，a342       

采用以纵为主序的方法存放， 即纵下标变化最慢， 行下标变化最快， 则顺序为：    

 a111，a211，a311，a121，a221，a321，…，a132，a232，a332，a142，a242，a342  

按上述两种方式顺序存储的数组，只要知道整个数组的起始地址、维数和每维的上下界，以及每个数组元素所占用的单元数，就可以将数组元素的存储地址表示为其下标的线性函数。

因此，顺序存储的数组是一种随机存取的结构。

3.二维数组的顺序存储

以二维数组Am×n为例，假设每个元素只占一个存储单元，“以行为主”存放数组，下标从1开始，首元素a11的地址为Loc［1, 1］，求任意元素aij的地址。aij是排在第i行，第j列，并且前面的第i-1行有n×（i-1）个元素，第ｉ行第j个元素前面还有ｊ-１个元素。

由此得到如下地址计算公式： Loc［i, j］=Loc［1, 1］+n×(i-1)+(j-1)

 根据计算公式，可以方便地求得aij的地址是Loc［i, j］。如果每个元素占size个存储单元，

则任意元素aij的地址计算公式为： Loc［i, j］=Loc［1, 1］ + (n×(i-1)+j-1)×size

4.三维数组的顺序存储

 三维数组A（1..r ,  1..m ,  1..n）可以看成是r个m×n的二维数组。

  假定每个元素占一个存储单元，采用以行为主序的方法存放，即行下标r变化最慢， 纵下标n变化最快。 首元素a111的地址为Loc［1, 1, 1］，求任意元素aijk的地址。        

显然，ai11的地址为Loc［i, 1, 1］=Loc［1, 1, 1］+(i-1)×m×n， 因为在该元素之前， 有ｉ-１个ｍ×ｎ的二维数组。由ai11的地址和二维数组的地址计算公式，不难得到三维数组任意元素aijk的地址：    

Loc［i, j, k］=Loc［1, 1, 1］+(i-1)×m×n+(j-1)×n+(k-1) 其中1≤i≤ｒ，1≤j≤ｍ， 1≤k≤ｎ。、

 如果将三维数组推广到一般情况，即：用j1、j2、j3代替数组下标i、j、k， 并且j1、j2、j3的下限为c1、c2、c3，上限分别为d1、 d2、d3，每个元素占一个存储单元，则三维数组中任意元素a(j1， j2，j3)的地址为：

Loc［j1, j2, j3］=Loc［c1, c2, c3］+l×(d2-c2+1)×(d3-c3+1)×(j1-c1) +l×(d3-c3+1)×(j2-c2)+l×(j3-c3)

其中l为每个元素所占存储单元数。

令α1=l×(d2-c2+1)×(d3-c3+1),  α2=l×(d3-c3+1), α3=1

则： Loc［j1, j2, j3］=Loc［c1, c2, c3］+α1×(j1-c1)+α2×(j2-c2)+α3(j3-c3)=Loc［c1, c2, c3］+∑αi×(ji-ci)     （1≤i≤3） 

 由公式可知Loc［j1, j2, j3］与j1, j2, j3呈线性关系。        

对于ｎ维数组A(c1∶d1, c2∶d2，…, cn∶dn)，我们只要把上式推广，就可以容易地得到ｎ维数组中任意元素aj1j2…jn的存储地址的计算公式: