10000hours

【DeepLizard】Pytorch神经网络编程学习笔记(第二部分)

视频地址（B站）：适用于初学者的PyTorch神经网络编程教学
课程官方博客地址：DEEPLIZARD
个人笔记第一部分：DeepLizard：Pytorch神经网络编程教学(第一部分)

说明：

笔记为个人学习笔记，如有错误，欢迎指正。
本篇笔记整理的内容为课程的第二部分，对应视频为 $P_{14}\sim P_{43}$
DeepLizard课程为全英文授课，B站视频为中文字幕，且每个视频都有配套的博客与课后测试题。

文章目录

Section 1：数据和数据处理
- P14：fashion-mnist数据集
- P15：使用torchvision演示一种简单的提取、转换和加载流程(ETL)
- - ETL过程
  - 使用PyTorch准备数据
  - - PyTorch Dataset Class
    - PyTorch DataLoader Class
- P16：使用DataSet和DataLoader
- - 查看数据
  - 访问训练集中的数据
  - PyTorch DataLoader：处理成批的数据
Section 2：神经网络和 PyTorch 设计
- P17：构建PyTorch CNN
- - 一些包和函数
  - 构建神经网络
- P18：CNN层，理解构建CNN时使用的参数
- - CNN层
  - CNN层参数
- P19：CNN内部的权重张量
- - 可学习参数
  - 获取实例网络
  - 访问层的权重
  - 权重张量形状
  - 权重矩阵
- P20：PyTorch可调用的神经网络模块，以及网络和层的前向方法是如何调用的
- - Linear类中的权重
  - 特殊的调用方法：__call()__函数
- P21：调试PyTorch源代码
- P22：实现一个卷积神经网络的前向方法
- P23：使用卷积神经网络由数据集的样本输入生成输出预测答案
- P24：将一批图像传递到网络并解释输出
- P25：一个输入张量在通过CNN的过程中的变化
- - CNN输出尺寸公式（方形）
  - CNN输出尺寸公式（非方形）
Section 3：训练神经网络
- P26：训练卷积神经网络（单个批次）
- - 训练卷积神经网络所需的步骤
  - 代码实现
- P27：构建一个卷积神经网络的训练循环
- P28：构建混淆矩阵
- P29：拼接张量和堆叠张量
- P30：使用tensorboard来可视化CNN在网络训练过程中的指标
- P31：神经网络超参数
- - 每次修改单个超参数值
  - 循环遍历不同的超参数值
  - 添加更多的参数
Section 4：神经网络实验#
- P32：编写Run Builder类，使不同的参数值生成多个运行
- P33：同步超参数测试
- P34：加速神经网络训练过程
- P35：使用 CUDA 训练神经网络
- - tensor with CUDA
  - network with CUDA
  - 检测系统中CUDA能否使用
  - GPU vs CPU
- P36：数据集规范化
- - 均值和标准差
  - 归一化和不归一化的效果区别
- P37：调试PyTorch 数据加载器源代码
- P38：使用Sequential类来建立神经网络的顺序
- - 准备工作
  - 建立神经网络的顺序
  - - 方式一
    - 方式二
    - 方式三
  - 使用Sequential类建一个Network类
  - - 原始Network
    - 方式一
    - 方式二
    - 方式三
    - 预测image
- P39：PyTorch 中的批处理规范
- - 创建网络
  - 准备数据
  - 测试
Section 5：补充学习
- P40：重置reset网络的权重
- - 重置单个层的权重
  - 重置网络中的层的权重
  - - all weights layer by layer
    - all weights using snapshot
    - all weights using re-initialization
- P41：改进测试框架
- P42：Max Pooling vs No Max Pooling
- P43：结束课程

Section 1：数据和数据处理

对应视频： $P_{14}\sim P_{16}$

P14：fashion-mnist数据集

略。

P15：使用torchvision演示一种简单的提取、转换和加载流程(ETL)

ETL过程

Extract data from a data source. 从数据源中提取数据。
Transform data into a desirable format. 将数据转换为所需的格式。
Load data into a suitable structure. 将数据加载到合适的结构中。

使用PyTorch准备数据

torchvision包，它可以使我们访问以下资源：Datasets；Models；Transforns；Utils

PyTorch Dataset Class

如要使用torchvision获取FashionMNIST数据集，可以通过以下代码实现：

train_set = torchvision.datasets.FashionMNIST(
    root='./data'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

参数	说明
root	磁盘上数据所在的位置
train	数据集是否是训练集
download	是否下载数据
transform	应对数据集元素执行的转换组合

当第一次运行完此代码后，FashionMNIST数据集将会下载到本地。

PyTorch DataLoader Class

为训练集创建一个DataLoader包装器：

train_loader = torch.utils.data.DataLoader(train_set
    ,batch_size=1000
    ,shuffle=True
)

P16：使用DataSet和DataLoader

查看数据

# 查看训练集中有多少图像
len(train_set) # 6000

# 查看每个图像的标签
train_set.targets # tensor([9, 0, 0,  ..., 3, 0, 5])

# 查看数据集中每个标签有多少个
train_set.targets.bincount() # tensor([6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000])

访问训练集中的数据

sample = next(iter(train_set))
len(sample) # 2

为访问训练集中的单个元素，先将train_set传给函数iter()，该函数返回一个表示数据流的对象，之后就可以用Python的内置函数next()来获取数据流中的下一个数据元素。

由函数的输出可知，每个样本(sample)包含两项，这是数据集中包含的图像标签对。可以使用序列解包来分配图像和标签：

image, label = sample
print(type(image)) # 
print(type(label)) #

查看元素：

print(image.shape) # torch.Size([1, 28, 28])
print(torch.tensor(label).shape) # torch.Size([])

# 调用squeeze（）,删除维度
print(image.squeeze().shape) # torch.Size([28, 28])

绘制图像：

plt.imshow(image.squeeze(), cmap='gray')
print(torch.tensor(label)) # tensor(0)
# 说明：这里sample为train_set[2]，也就是第三个元素，它的标签为0，对照上面的train_set.targets输出，可以看到第三个图像的标签就是0

PyTorch DataLoader：处理成批的数据

# 先创建一个批处理大小为10的数据加载程序：
display_loader = torch.utils.data.DataLoader(train_set, batch_size = 10)

# 注意：当shuffle=True时，每个batch都会不同
batch = next(iter(display_loader))
print(len(batch)) # 2

# 查看返回批次的长度
images, labels = batch
print(type(images)) #  
print(type(labels)) # 
print(images.shape) # torch.Size([10, 1, 28, 28]) # (批量大小，颜色通道数，图像高度，图像宽度) 
print(labels.shape) # torch.Size([10])

绘制一批图像：

# 绘制一批图像
# 方法一：
grid = torchvision.utils.make_grid(images, nrow=10)
plt.figure(figsize=(15,15))
plt.imshow(np.transpose(grid, (1,2,0)))

# 方法二：
grid = torchvision.utils.make_grid(images, nrow=10)
plt.figure(figsize=(15,15))
plt.imshow(grid.permute(1,2,0))

Section 2：神经网络和 PyTorch 设计

P17：构建PyTorch CNN

一些包和函数

nn.Module
PyTorch的神经网络库中包含了构建神经网络所需的所有典型组件。深度神经网络是使用多层构建的，神经网络中每一层都有两个主要组成部分：变换（代码），权重的集合（数据）。

PyTorch中的nn.Module是所有包含层的神经网络模块的基类，这意味着PyTorch中的所有层都扩展了nn.Module。
forward()
前向传播：当把一个张量传递给我们的网络作为输入，张量通过每个层变换向前流动，直到张量达到输出层。这个通过网络向前流动的张量的过程被称为前向传播。

每一层都有它自己的变换，张量向前通过每一层的变换。所有单独的层的前向传播的组合定义了网络本身的整体向前转换。

在PyTorch中，每个nn.module都有一个前向方法来代表前向传输。因此在神经网络中构建层时，必须提供前向方法（forward method）的实现，前向方法就是实际的变换。
nn.functional
nn.functional包为我们提供了许多可用于构建层的神经网络操作。

构建神经网络

在 PyTorch 中构建神经网络的大纲：

创建一个扩展神经网络模块基类的神经网络类
在类构造函数中将网络的层定义为类属性
使用网络层属性以及nn.functional API的操作来定义网络的前向传播forward()

import torch.nn as nn

# 基础版
class Network:
    def __init__(self):
        self.layer = None # 层
        
    def forward(self, t): # 前向传播函数
        t = self.layer(t)
        return t
    
# 进阶版
class Netword(nn.Module): # 定义一个扩展基类的神经网络类
    def __init__(self):
        super().__init__()
        # 卷积层
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
        
        # 线性层
        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Lineat(in_features=60, out_features=10)
        
    def forward(self, t): 
        # t = self.layer(t)
        return t

P18：CNN层，理解构建CNN时使用的参数

CNN层

在P17中，我们定义了两个卷积层和三个线性层。我们的每一层都扩展了PyTorch的神经网络模块基类。

对于每一层，有两个主要项目封装其中：前向函数定义和权重张量。每层中的权重张量包含了随着我们的网络在训练过程中学习而更新的权重值。在神经网络模块类中，PyTorch可以跟踪每一层的权重张量。由于我们扩展了神经网络模块基类，我们自动继承了这个功能。

CNN层参数

parameter 和 argument

parameter在函数定义中使用，由于这个原因，我们可以把参数看成是占位符。
argument是当函数被调用时传递给函数的实际值。
或者说，parameter是形参，argument是实参
超参数和数据相关超参数
超参数的值是手动设置和任意选择的，主要是根据试错来选择超参数的值，并更多地使用过去已被证明有效的值。e.g. CNN层中的超参数
- kernel_size：内核大小设置了在该层中使用的滤波器的大小。（在DL中，内核kernel和滤波器filter是一个意思，所以卷积核和卷积滤波器是一个东西）
- out_channels：设置滤波器的深度。这是滤波器的内核数。（在一个卷积层中，输入通道与一个卷积滤波器配对来执行卷积运算。滤波器包含输入通道，这个操作的结果是一个输出通道。所以一个包含输入通道的滤波器可以给我们一个相应的输出通道。因此我们在设置输出通道数时，其实是在设置滤波器的数量。）
- out_features：设置输出张量的大小。
数据相关超参数是其值依赖于数据的参数。e.g. 第一个卷积层in_channels和输出层out_features。

P19：CNN内部的权重张量

可学习参数

可学习参数是在训练过程中学习的参数。对于可学习参数，通常重一组任意的值开始，当网络学习时，这些值就会以迭代的方式更新。

可学习参数是网络内部的权重，它们存在于每一层中。

获取实例网络

network = Network()
print(network)

# 输出
Network(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=192, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=60, bias=True)
  (out): Linear(in_features=60, out_features=10, bias=True)
)

kernel_size=(5, 5)：当我们传递单个数字时，层构造函数假定我们想要的是一个方形滤波器。
stride=(1, 1)：告诉conc层在每次卷积操作后滤波器应该滑动多远。

访问层的权重

network.conv1.weight

其输出是一个张量，其中的值或标量分量是我们网络的可学习参数。当网络训练时，这些权重值会以一种方式更新，以使损失函数最小化。

权重张量形状

传递给层的参数值将直接影响网络的权重。

对于卷积层，权重值位于滤波器内部，在代码中，滤波器实际上是权重张量本身。层内的卷积操作是层的输入通道与层内的滤波器之间的操作。

network.conv1.weight.shape
# 输出：torch.Size([6, 1, 5, 5])

第一个轴的长度为6，这说明有6个滤波器。
第二个轴的长度为1，说明只有单个输入通道。
第三、四个轴的数值代表滤波器的高度和宽度。

network.conv2.weight.shape
# 输出：torch.Size([12, 6, 5, 5])

第二个conv层有12个滤波器，说明有来自前一层的6个输入通道。
可以将值6看做是赋予每个滤波器一定的深度，滤波器没有迭代的卷积所有的通道，而是具有与通道数相匹配的深度。

关于这些卷积层的两个要点：滤波器使用一个张量来表示，张量内的每个滤波器也有一个深度来说明正在卷积的输入通道数。

这里的张量是秩为4的张量，第一个轴表示滤波器的数量；第二个轴表示每个滤波器的深度，对应于被卷积的输入通道数量；最后两个轴表示每个滤波器的高和宽。
$(滤波器数量，深度，高度，宽度)$

权重矩阵

network.fc1.weight.shape # torch.Size([120, 192])
network.fc2.weight.shape # torch.Size([60, 120])
network.out.weight.shape # torch.Size([10, 60])
len(network.out.weight.shape) # 2

每个线性层都有一个秩为2的权重张量。以fc1的权重张量为例，由权重张量的形状可知，row120是输出特征的大小，column192是输入特征的大小，也就是说，权重张量的形状是根据输入特征和输出特征的大小得来的。通过矩阵乘法来直观感受：

线性层使用矩阵乘法来将它们的输入特征转换为输出特征：当输入特征被线性层接收时，它们以一个扁平的一维张量的形式传递，然后乘以权重矩阵，得到的结果就是输出特征。

这就是线性层的工作原理：它们使用一个权重矩阵将一个输入特征空间映射到一个输出特征空间。

P20：PyTorch可调用的神经网络模块，以及网络和层的前向方法是如何调用的

Linear类中的权重

定义输入特征和权重矩阵：

import torch

in_features = torch.tensor([1,2,3,4], dtype=torch.float32)

weight_matrix = torch.tensor([
    [1,2,3,4],
    [2,3,4,5],
    [3,4,5,6]
],dtype=torch.float32)

执行矩阵乘法，由P19的内容可知，得到的输出就是输出特征out_features：

weight_matrix.matmul(in_features)
# 输出：tensor([30., 40., 50.])

定义一个线性层，输入特征大小为4，输出特征大小为3：

fc = nn.Linear(in_features=4, out_features=3)

这一步要注意的是：通过使用权重矩阵将4维空间映射到3维空间。权重矩阵位于PyTorch线性层类中，由PyTorch创造，PyTorch线性层类通过将4和3传递给构造函数，以创建一个3x4的权重矩阵

调用对象实例

fc(in_features)
# 输出：tensor([ 0.2730, -0.4860, -1.7627], grad_fn=)

这里的值[ 0.2730, -0.4860, -1.7627]与[30., 40., 50.]相差甚远，这是因为PyTorch创建了一个权重矩阵，并用随机值来初始化。

权重矩阵中的值定义了一个线性函数( $y = A x + b$ )。这表明了在训练过程中，当权重被更新时，网络的映射是如何变化的，当更新权重时，我们在改变函数（更改了 $A$ 和 $b$ ）。

再使用新的输入进行测试：

fc.weight = nn.Parameter(weight_matrix)
fc(in_features)
# 输出：tensor([30.4673, 40.0535, 50.3319], grad_fn=)

输出结果更接近[30,40,50]但又不完全相等，这是因为有偏置值的存在。

特殊的调用方法：call()函数

如果一个类实现了特殊的__call()__方法，每当调用对象实例时，都会调用__call()__方法。

我们不直接调用前向方法forward()，而是调用对象实例，在调用对象实例之后，__call()__方法会被调用，而__call()__方法又反过来调用forward()方法。

PyTorch在__call()__方法中运行的额外代码是我们从未直接调用forward()方法的原因：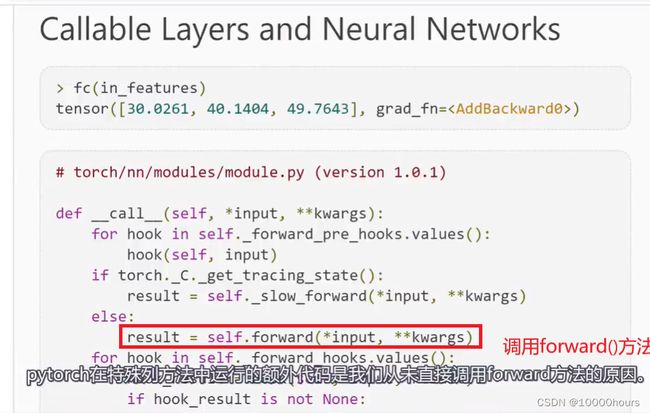

P21：调试PyTorch源代码

略

P22：实现一个卷积神经网络的前向方法

我们的forward()方法接收一个张量作为输入，然后返回一个张量作为输出。

forward()方法的实现将使用我们在构造函数中定义的所有层。forward()方法是输入张量到一个预测的输出张量的映射。

关于input layer：

任何神经网络的输入层都是由输入数据决定的。
比如，若输入张量中包含三个元素，那网络将有三个节点包含在它的输入层中，因此可将输入层看做恒等转换（ $f (x) = x$ ）
输入层通常隐藏。但在以下代码中，将输入层用代码显示表示出来：t = t

import torch  
import torch.nn as nn  
import torch.nn.functional as F  
  
class Network(nn.Module):  
    def __init__(self):  
        super().__init__()  
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)  
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)  
  
        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)  
        self.fc2 = nn.Linear(in_features=120, out_features=60)  
        self.out = nn.Linear(in_features=60, out_features=10)  
  
    def forward(self, t):  
        # （1）输入层input layer(输入层在代码中通常隐藏)  
        t = t  
  
        # （2）卷积层 hidden conv layer        t = self.conv1(t) # 其中封装了权重  
        t = F.relu(t)  
        t = F.max_pool2d(t, kernel_size=2, stride=2)  
  
        # （3）卷积层 hidden conv layer        t = self.conv2(t) # 其中封装了权重  
        t = F.relu(t)  
        t = F.max_pool2d(t, kernel_size=2, stride=2)  
  
        # 注：每层都由一组权重和一组操作组成。  
        # 权重被封装在神经网络模块层类实例中：e.g. self.conv1(t)  
        # relu()和max_pool2d()都是操作  
  
        # 在把输入传递给第一个线性层之前，必须重塑张量。每当把卷积层的输出输入到一个线性层时，就会出现这种情况  
  
        # （4）线性层 hidden liner layer        # 12是由之前的卷积层产生的输出通道数决定的  
        # 4 * 4是12个输出通道的高和宽  
        t = t.reshape(-1, 12 * 4 * 4)  
        t = self.fc1(t)  
        t = F.relu(t)  
  
        # （5）线性层 hidden liner layer        t = self.fc2(t)  
        t = F.relu(t)  
  
        # （6）输出层 output layer        t = self.out(t)  
        t = F.softmax(t, dim=1)  
  
        return t

P23：使用卷积神经网络由数据集的样本输入生成输出预测答案

再来理解一下前向传播：

前向传播是将输入张量转换为输出张量的过程。
神经网络是将输入张量映射到输出张量的函数，而前向传播只是将输入张量传递给网络并从网络接收输出的过程的一个特殊名称。

代码实现：

import torch
import torch.nn as nn
import torch.nn.functional as F

import torchvision
import torchvision.transforms as transforms

torch.set_printoptions(linewidth=120)

# 建立训练集
train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

# 建立模型
class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        # （1）输入层input layer(输入层在代码中通常隐藏)
        t = t

        # （2）卷积层 hidden conv layer
        t = self.conv1(t) # 其中封装了权重
        t = F.relu(t)
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        # （3）卷积层 hidden conv layer
        t = self.conv2(t) # 其中封装了权重
        t = F.relu(t)
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        # 注：每层都由一组权重和一组操作组成。
        # 权重被封装在神经网络模块层类实例中：e.g. self.conv1(t)
        # relu()和max_pool2d()都是操作

        # 在把输入传递给第一个线性层之前，必须重塑张量。每当把卷积层的输出输入到一个线性层时，就会出现这种情况

        # （4）线性层 hidden liner layer
        # 12是由之前的卷积层产生的输出通道数决定的
        # 4 * 4是12个输出通道的高和宽
        t = t.reshape(-1, 12 * 4 * 4)
        t = self.fc1(t)
        t = F.relu(t)

        # （5）线性层 hidden liner layer
        t = self.fc2(t)
        t = F.relu(t)

        # （6）输出层 output layer
        t = self.out(t)
        t = F.softmax(t, dim=1)

        return t

# 关闭PyTorch的梯度跟踪功能
torch.set_grad_enabled(False)

# 创建一个网络实例
network = Network()

# 获取样本并解压
sample = next(iter(train_set))
image, label = sample # image.shape:[1,28,28]，一个颜色通道，高度和宽度均为28

# 当把数据传给网络时，网络期待的是一批数据，因此要将这些单张图像转换为一个批次
# 把单个样本图像张量放入一个大小为1的批次中，只需unsqueeze()方法来为张量增加一个额外的维度
image.unsqueeze(0) # [1, 1, 28, 28]，批次大小为1


# 预测
pred = network(image.unsqueeze(0)) # 图像的形状应为(batch_size * in_channels * H * W)

# 至此，通过使用前向方法从网络得到了一个预测
# 网络返回一个预测张量，它包含了10个类别的预测值
print(pred) # tensor([[0.1183, 0.1015, 0.0903, 0.0977, 0.1076, 0.1084, 0.0925, 0.0954, 0.0982, 0.0901]])

P24：将一批图像传递到网络并解释输出

import torch
import torch.nn as nn
import torch.nn.functional as F

import torchvision
import torchvision.transforms as transforms

#torch.set_printoptions(linewidth=120)


# 建立模型
class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        # （1）输入层input layer(输入层在代码中通常隐藏)
        t = t

        # （2）卷积层 hidden conv layer
        t = self.conv1(t) # 其中封装了权重
        t = F.relu(t)
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        # （3）卷积层 hidden conv layer
        t = self.conv2(t) # 其中封装了权重
        t = F.relu(t)
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        # 注：每层都由一组权重和一组操作组成。
        # 权重被封装在神经网络模块层类实例中：e.g. self.conv1(t)
        # relu()和max_pool2d()都是操作

        # 在把输入传递给第一个线性层之前，必须重塑张量。每当把卷积层的输出输入到一个线性层时，就会出现这种情况

        # （4）线性层 hidden liner layer
        # 12是由之前的卷积层产生的输出通道数决定的
        # 4 * 4是12个输出通道的高和宽
        t = t.reshape(-1, 12 * 4 * 4)
        t = self.fc1(t)
        t = F.relu(t)

        # （5）线性层 hidden liner layer
        t = self.fc2(t)
        t = F.relu(t)

        # （6）输出层 output layer
        t = self.out(t)
        t = F.softmax(t, dim=1)

        return t

# 关闭PyTorch的梯度跟踪功能
torch.set_grad_enabled(False)

# 创建一个网络实例
network = Network()

# 建立训练集
train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=False
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

# 数据加载器
data_loader = torch.utils.data.DataLoader(
    train_set
    ,batch_size=10
)

batch = next(iter(data_loader)) # 一次返回10张图像
images, labels = batch # image.shape:[10, 1, 28, 28]; labels.shape:[10]

# 预测
preds = network(images)
# preds.shape:[10, 10]，有10张图像，对于这10张图，有10个预测类

将预测类别与标签进行比较：

# 将预测值与标签进行比较
preds.argmax(dim=1).eq(labels)
# 输出：tensor([False, False, False, False, False,  True, False,  True, False, False])
# 只有两个预测正确

P25：一个输入张量在通过CNN的过程中的变化

CNN输出尺寸公式（方形）

假设输入尺寸为 $n\times n$
假设滤波器尺寸为 $f\times f$
假设填充padding为 $p$ ，步长stride为 $s$
输出尺寸 $O$ 的计算公式为：
$\frac{n-f+2p}{s} + 1$

以我们之前构建的的CNN为例，输入张量在通过CNN的过程中的尺寸变化如下：

操作	输出尺寸
初始输入	[1,1,28,28]
卷积（ $5\times5$ ）	[1,6,24,24
最大池化（ $2\times2$ ）	[1,6,12,12]
卷积（ $5\times5$ ）	[1,12,8,8]
最大池化（ $2\times2$ ）	[1,12,4,4]
Flatten展平	[1,192]( $192 = 12 * 4 * 4$ )
线性转换	[1,120]
线性转换	[1,60]
线性转换	[1,10]
可以将值带入计算一下。

CNN输出尺寸公式（非方形）

假设输出尺寸为 $n_h\times n_w$
假设滤波器尺寸为 $f_h\times f_w$
假设填充padding为 $p$ ，步长stride为 $s$
输出尺寸的高度 $O_h$ 为：
$O_h=\frac{n_h-f_h+2p}{s}+1$
输出尺寸的宽度 $O_w$ 为：
$O_w= \frac{n_w-f_w+2p}{s}+1$

Section 3：训练神经网络

对应视频： $P_{26}\sim P_{31}$

P26：训练卷积神经网络（单个批次）

训练卷积神经网络所需的步骤

从训练集中得到一批数据
将这批数据传递给网络
计算损失
计算损失函数的梯度和网络的权值
更新权重，使用梯度来减少损失
重复1~5，直到一个epoch完成
重复1~6，以获得所期望的精度

代码实现

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torchvision
import torchvision.transforms as transforms

torch.set_printoptions(linewidth=120) # 设置输出行宽
torch.set_grad_enabled(True) # 默认情况下即为True，开启梯度跟踪功能

def get_num_correct(preds, labels):
    return preds.argmax(dim=1).eq(labels).sum().item()

class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        t = F.relu(self.conv1(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = F.relu(self.conv2(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = t.reshape(-1, 12 * 4 * 4)
        t = F.relu(self.fc1(t))

        t = F.relu(self.fc2(t))

        t = self.out(t)

        return t

train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

# 单批次训练
network = Network()

train_loader = torch.utils.data.DataLoader(train_set, batch_size=100)
optimizer = optim.Adam(network.parameters(), lr=0.01)

batch = next(iter(train_loader)) # 获取批次
images, labels = batch

preds = network(images) # 传递批次
loss = F.cross_entropy(preds, labels) # 计算损失

loss.backward() # 计算梯度
optimizer.step() # 更新梯度

# 打印损失和预测正确的图像数
print('loss1:', loss.item())
print('correct1:',get_num_correct(preds, labels))
preds = network(images)
loss = F.cross_entropy(preds, labels)
print('loss2:',loss.item())
print('correct2:',get_num_correct(preds, labels))

输出结果：

loss1: 2.3046135902404785
correct1: 11
loss2: 2.288461208343506
correct2: 11

以上都是针对单个批次的训练

P27：构建一个卷积神经网络的训练循环

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torchvision
import torchvision.transforms as transforms

torch.set_printoptions(linewidth=120) # 设置输出行宽
torch.set_grad_enabled(True) # 默认情况下即为True，开启梯度跟踪功能

def get_num_correct(preds, labels):
    return preds.argmax(dim=1).eq(labels).sum().item()

class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        t = F.relu(self.conv1(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = F.relu(self.conv2(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = t.reshape(-1, 12 * 4 * 4)
        t = F.relu(self.fc1(t))

        t = F.relu(self.fc2(t))

        t = self.out(t)

        return t

train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=False
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

# Training Loop
network = Network()

train_loader = torch.utils.data.DataLoader(train_set, batch_size=100)
optimizer = optim.Adam(network.parameters(), lr=0.01)

for epoch in range(5):
    total_loss = 0
    total_correct = 0
    for batch in train_loader:
        images, labels = batch

        preds = network(images) # 传递批次
        loss = F.cross_entropy(preds, labels) # 计算损失

        optimizer.zero_grad() # 告诉优化器把梯度属性中的权重的梯度归零，这是因为pytorch会积累梯度，
        loss.backward() # 计算梯度
        optimizer.step() # 更新梯度

        total_loss += loss.item()
        total_correct += get_num_correct(preds, labels)

    print('epoch:', epoch, 'total_correct:', total_correct, 'loss:', total_loss)

print(total_correct / len(train_set))

输出结果：

epoch: 0 total_correct: 46839 loss: 345.08213037252426
epoch: 1 total_correct: 51307 loss: 234.14958696067333
epoch: 2 total_correct: 51962 loss: 215.7918103337288
epoch: 3 total_correct: 52259 loss: 206.81365805864334
epoch: 4 total_correct: 52613 loss: 198.79174283146858
0.8768833333333333

注：

为什么优化器可以更新权重？因为优化器知道网络的权重，我们将权重传递给优化器构造器。
在视频的11:00左右，作者进行代码调试，可以清晰的看到梯度和权重的变化。

P28：构建混淆矩阵

要创建混淆矩阵，需要一个预测张量和一个有相应真值或标签的张量。

def get_all_preds(model, loader):
    all_preds = torch.tensor([])
    for batch in loader:
        images, labels = batch
        
        preds = model(images)
        all_preds = torch.cat( # 将这些预测连接起来
            (all_preds, preds)
            , dim=0
        )
    return all_preds

prediction_loader = torch.utils.data.DataLoader(train_set, batch_size=10000)
train_preds = get_all_preds(network, prediction_loader) # 包含了训练集中每个样本的预测

# 需要在不跟踪梯度的情况下的得到我们的预测，或者不需要创建图表,使用更少的内存
with torch.no_grad():
    prediction_loader = torch.utils.data.DataLoader(train_set, batch_size=10000)
    train_preds = get_all_preds(network, prediction_loader)

preds_correct = get_num_correct(train_preds, train_set.targets)
print('total correct:',preds_correct)
print('accuracy:', preds_correct / len(train_set))

# 输出
total correct: 51211
accuracy: 0.8535166666666667

接下来，建立混淆矩阵，需要标签以及一个相应的预测张量

print(train_set.targets)
print(train_preds.argmax(dim=1))
# 输出
tensor([9, 0, 0,  ..., 3, 0, 5])
tensor([9, 0, 0,  ..., 3, 0, 5])

接下来我们需要将这些预测标签和目标标签配对：

stacked = torch.stack(
    (
        train_set.targets
        ,train_preds.argmax(dim=1)
    )
    ,dim=1
)

接着，创建一个空的矩阵，并将数据导入空矩阵：

# 创建一个混淆矩阵
cmt = torch.zeros(10,10,dtype=torch.int64) # 10 * 10

for p in stacked:
    true_label, pred_label = p.tolist()
    cmt[true_label, pred_label] = cmt[true_label, pred_label] + 1 # 实际上是要计算相应类别的出现次数

查看这个混淆矩阵：

tensor([[5626,    0,   35,   55,   14,    2,  231,    0,   36,    1],
        [  80, 5752,    4,  132,    5,    2,   13,    0,   12,    0],
        [ 142,    0, 4003,   59, 1086,    1,  667,    1,   41,    0],
        [ 537,    9,    6, 5096,  164,    1,  183,    0,    3,    1],
        [  24,    3,  166,  238, 4764,    0,  781,    2,   22,    0],
        [   1,    0,    2,    6,    0, 5347,    0,  496,   36,  112],
        [1627,    2,  368,   81,  394,    1, 3440,    0,   87,    0],
        [   0,    0,    0,    0,    0,    5,    0, 5914,   15,   66],
        [  65,    0,   13,   32,   33,   10,   31,    4, 5806,    6],
        [   1,    0,    0,    1,    0,   10,    0,  524,    1, 5463]])

下面展示一种通过调包的方式画出混淆矩阵

# 画一个混淆矩阵,使用包
import matplotlib.pyplot as plt

from sklearn.metrics import confusion_matrix
# from plotcm import plot_confusion_matrix

import itertools
import numpy as np
import matplotlib.pyplot as plt

def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues):
    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
        print("Normalized confusion matrix")
    else:
        print('Confusion matrix, without normalization')

    print(cm)
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=45)
    plt.yticks(tick_marks, classes)

    fmt = '.2f' if normalize else 'd'
    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, format(cm[i, j], fmt), horizontalalignment="center", color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

cm = confusion_matrix(train_set.targets, train_preds.argmax(dim=1))
print(type(cm))
print(cm)

# 打印
<class 'numpy.ndarray'>
array([[5626,    0,   35,   55,   14,    2,  231,    0,   36,    1],
       [  80, 5752,    4,  132,    5,    2,   13,    0,   12,    0],
       [ 142,    0, 4003,   59, 1086,    1,  667,    1,   41,    0],
       [ 537,    9,    6, 5096,  164,    1,  183,    0,    3,    1],
       [  24,    3,  166,  238, 4764,    0,  781,    2,   22,    0],
       [   1,    0,    2,    6,    0, 5347,    0,  496,   36,  112],
       [1627,    2,  368,   81,  394,    1, 3440,    0,   87,    0],
       [   0,    0,    0,    0,    0,    5,    0, 5914,   15,   66],
       [  65,    0,   13,   32,   33,   10,   31,    4, 5806,    6],
       [   1,    0,    0,    1,    0,   10,    0,  524,    1, 5463]],
      dtype=int64)

names = ('T-shirt','Trouser','Pullover','Dress','Coat','Sandal','Shirt','Sneaker','Bag','Ankel boot')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, names)

输出：

Confusion matrix, without normalization
[[5626    0   35   55   14    2  231    0   36    1]
 [  80 5752    4  132    5    2   13    0   12    0]
 [ 142    0 4003   59 1086    1  667    1   41    0]
 [ 537    9    6 5096  164    1  183    0    3    1]
 [  24    3  166  238 4764    0  781    2   22    0]
 [   1    0    2    6    0 5347    0  496   36  112]
 [1627    2  368   81  394    1 3440    0   87    0]
 [   0    0    0    0    0    5    0 5914   15   66]
 [  65    0   13   32   33   10   31    4 5806    6]
 [   1    0    0    1    0   10    0  524    1 5463]]

混淆矩阵：

P29：拼接张量和堆叠张量

拼接是在一个现有的轴上连接一系列张量，堆叠是在一个新的轴上连接一系列的张量。

如何选择拼接还是堆叠？
假设现有三个图像张量，每个都有三个轴，每个张量都是相互独立的：

假设我们的任务是将这些张量结合在一起形成一个三个图像的单张量。
在这个例子中，只有三个维度，但对于一批数据，需要四个维度，所以说要沿着一个新的轴将张量堆叠起来，新轴就是批次轴：

如果沿着任何现有的轴将这个张量拼接起来，我们就会把颜色通道、高度或宽度弄乱。
假设图像已有了批处理的一个维度，这意味着我们有三个批次，其大小为1：

假设我们的任务是获得一批三张图像。我们可以在批处理维度上进行拼接：

代码演示：

# stack VS cat
import torch
t1 = torch.tensor([1,1,1])
t2 = torch.tensor([2,2,2])
t3 = torch.tensor([3,3,3])

torch.cat(
    (t1,t2,t3)
    ,dim=0
)
# 在现有的轴上进行拼接
tensor([1, 1, 1, 2, 2, 2, 3, 3, 3])

torch.stack(
    (t1,t2,t3)
    ,dim=0
)
# 创建一个新轴，并沿着这个轴将这些张量堆叠起来
tensor([[1, 1, 1],
        [2, 2, 2],
        [3, 3, 3]])

P30：使用tensorboard来可视化CNN在网络训练过程中的指标

tensorboard是tensorflow的可视化工具，它是一个前端web界面，从一个文件中读取数据，然后显示它。它使我们能跟踪和可视化度量标准，比如我们的损失和准确率，还能可视化我们的网络图。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import torchvision
import torchvision.transforms as transforms

torch.set_printoptions(linewidth=120) # 设置输出行宽
torch.set_grad_enabled(True) # 默认情况下即为True，开启梯度跟踪功能

from torch.utils.tensorboard import SummaryWriter

def get_num_correct(preds, labels):
    return preds.argmax(dim=1).eq(labels).sum().item()

class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        t = F.relu(self.conv1(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = F.relu(self.conv2(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = t.reshape(-1, 12 * 4 * 4)
        t = F.relu(self.fc1(t))

        t = F.relu(self.fc2(t))

        t = self.out(t)

        return t

# train_set = './PyTorchLearning/data/FashionMNIST'
train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=False
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

train_loader = torch.utils.data.DataLoader(train_set, batch_size=100, shuffle=True)

#------------------------------------------
tb = SummaryWriter()

network = Network()
images, labels = next(iter(train_loader))
grid = torchvision.utils.make_grid(images)

tb.add_image('images', grid)
tb.add_graph(network, images)
tb.close()
#------------------------------------------

运行上述代码之后，在根目录下会出现一个名为runs的文件夹:
进入终端，并进入根目录，之后执行指令tensorboard --logdir=runs，将http://localhost:6006/粘贴到浏览器打开，就可以看到界面了。

tensorboard界面

（1）首先可以看到IMAEGS界面已经出现了图片：

（2）在GRAPHS界面可以看到我们的网络图：

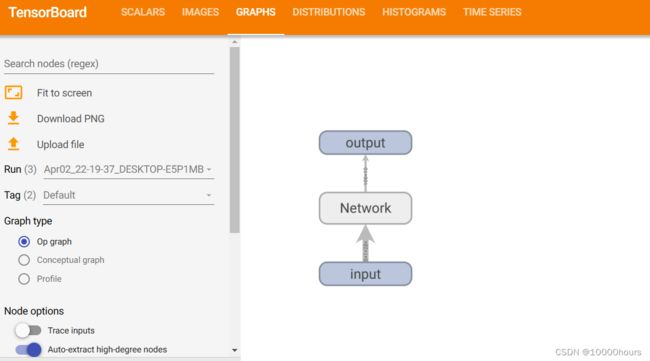
双击可以看到里面的详细结构：

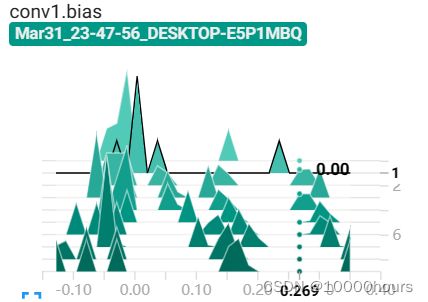
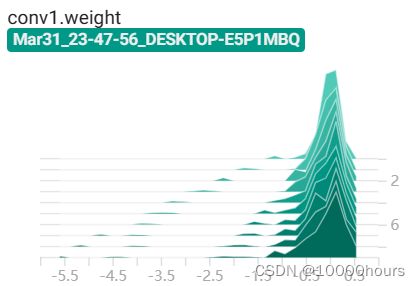
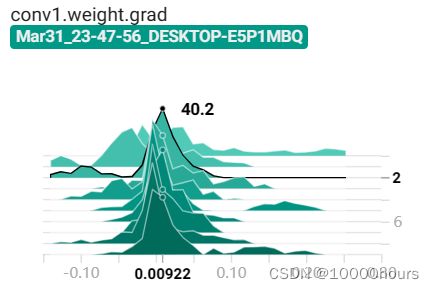
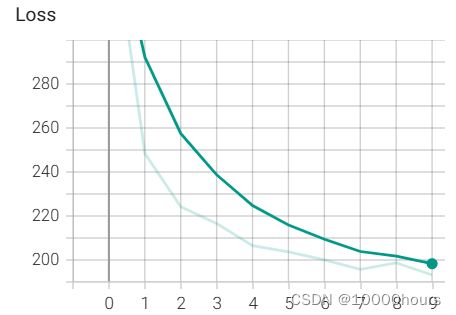
（3）将单批次训练改为循环。循环的代码如下：

# LOOP
network = Network()
optimizer = optim.Adam(network.parameters(), lr=0.01)

images, labels = next(iter(train_loader))
grid = torchvision.utils.make_grid(images)

tb = SummaryWriter()
tb.add_image('images', grid)
tb.add_graph(network, images)

for epoch in range(5):
    total_loss = 0
    total_correct = 0
    for batch in train_loader:
        images, labels = batch

        preds = network(images) # 传递批次
        loss = F.cross_entropy(preds, labels) # 计算损失

        optimizer.zero_grad() # 告诉优化器把梯度属性中的权重的梯度归零，这是因为pytorch会积累梯度，
        loss.backward() # 计算梯度
        optimizer.step() # 更新梯度

        total_loss += loss.item()
        total_correct += get_num_correct(preds, labels)

    # 添加值
    tb.add_scalar('Loss', total_loss, epoch)
    tb.add_scalar('Number Correct', total_correct, epoch)
    tb. add_scalar('Accuracy', total_correct / len(train_set), epoch)

    # 创建直方图
    tb.add_histogram('conv1.bias', network.conv1.bias, epoch)
    tb.add_histogram('conv1.weight', network.conv1.weight, epoch)
    tb.add_histogram('conv1.weight.grad', network.conv1.weight.grad, epoch)

    print('epoch:', epoch, 'total_correct:', total_correct, 'loss:', total_loss)
tb.close()

运行结束后刷新tensorboard界面，可以看到新增的条目：

<1>SCALARS界面：

<2>HSITOGRAMS界面：
||
—|—|—

P31：神经网络超参数

每次修改单个超参数值

batch_size = 100
lr = 0.01

network = Network()
train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size, shuffle=True)
optimizer = optim.Adam(network.parameters(), lr=lr)

images, labels = next(iter(train_loader))
grid = torchvision.utils.make_grid(images)

comment = f'batch_size={batch_size} lr={lr}' # 添加注释字符串
tb = SummaryWriter(comment=comment)
tb.add_image('images', grid)
tb.add_graph(network, images)

for epoch in range(5):
    total_loss = 0
    total_correct = 0
    for batch in train_loader:
        images, labels = batch

        preds = network(images) # 传递批次
        loss = F.cross_entropy(preds, labels) # 计算损失

        optimizer.zero_grad() # 告诉优化器把梯度属性中的权重的梯度归零，这是因为pytorch会积累梯度，
        loss.backward() # 计算梯度
        optimizer.step() # 更新梯度

        total_loss += loss.item() * batch_size # 调整损失计算
        total_correct += get_num_correct(preds, labels)

    # 添加值
    tb.add_scalar('Loss', total_loss, epoch)
    tb.add_scalar('Number Correct', total_correct, epoch)
    tb. add_scalar('Accuracy', total_correct / len(train_set), epoch)

    # 添加所有参数
    for name, weight in network.named_parameters():
        tb.add_histogram(name, weight, epoch)
        tb.add_histogram(f'{name}.grad', weight.grad, epoch)


    print('epoch:', epoch, 'total_correct:', total_correct, 'loss:', total_loss)

tb.close()

循环遍历不同的超参数值

batch_size_list = [100, 1000, 10000]
lr_list = [0.01, 0.001, 0.0001, 0.00001]

for batch_size in batch_size_list:
    for lr in lr_list:
        network = Network()

        train_loader = torch.utils.data.DataLoader(
            train_set, batch_size=batch_size
        )
        optimizer = optim.Adam(
            network.parameters(), lr=lr
        )

        images, labels = next(iter(train_loader))
        grid = torchvision.utils.make_grid(images)

        comment = f'batch_size={batch_size} lr={lr}'  # 添加注释字符串
        tb = SummaryWriter(comment=comment)
        tb.add_image('images', grid)
        tb.add_graph(network, images)

        for epoch in range(5):
            total_loss = 0
            total_correct = 0
            for batch in train_loader:
                images, labels = batch

                preds = network(images)  # 传递批次
                loss = F.cross_entropy(preds, labels)  # 计算损失

                optimizer.zero_grad()  # 告诉优化器把梯度属性中的权重的梯度归零，这是因为pytorch会积累梯度，
                loss.backward()  # 计算梯度
                optimizer.step()  # 更新梯度

                total_loss += loss.item() * batch_size  # 调整损失计算
                total_correct += get_num_correct(preds, labels)

            # 添加值
            tb.add_scalar('Loss', total_loss, epoch)
            tb.add_scalar('Number Correct', total_correct, epoch)
            tb.add_scalar('Accuracy', total_correct / len(train_set), epoch)

            # 添加所有参数
            for name, weight in network.named_parameters():
                tb.add_histogram(name, weight, epoch)
                tb.add_histogram(f'{name}.grad', weight.grad, epoch)

            print('epoch:', epoch, 'total_correct:', total_correct, 'loss:', total_loss)

        tb.close()

添加更多的参数

创建一个参数字典，并使用product函数，生成参数
之间的笛卡尔积，然后遍历。

from itertools import product

parameters = dict(
    lr = [0.01, 0.001]
    ,batch_size = [10, 100, 1000]
    ,shuffle = [True, False]
)

param_values = [v for v in parameters.values()]

for lr, batch_size, shuffle in product(*param_values):
    print(lr, batch_size, shuffle)
    # comment = f'batch_size={batch_size} lr={lr} shuffle={shuffle}'

    network = Network()

    train_loader = torch.utils.data.DataLoader(
        train_set, batch_size=batch_size
    )
    optimizer = optim.Adam(
        network.parameters(), lr=lr
    )

    images, labels = next(iter(train_loader))
    grid = torchvision.utils.make_grid(images)

    comment = f'batch_size={batch_size} lr={lr} shuffle={shuffle}'
    tb = SummaryWriter(comment=comment)
    tb.add_image('images', grid)
    tb.add_graph(network, images)

    for epoch in range(5):
        total_loss = 0
        total_correct = 0
        for batch in train_loader:
            images, labels = batch

            preds = network(images)  # 传递批次
            loss = F.cross_entropy(preds, labels)  # 计算损失

            optimizer.zero_grad()  # 告诉优化器把梯度属性中的权重的梯度归零，这是因为pytorch会积累梯度，
            loss.backward()  # 计算梯度
            optimizer.step()  # 更新梯度

            total_loss += loss.item() * batch_size  # 调整损失计算
            total_correct += get_num_correct(preds, labels)

        # 添加值
        tb.add_scalar('Loss', total_loss, epoch)
        tb.add_scalar('Number Correct', total_correct, epoch)
        tb.add_scalar('Accuracy', total_correct / len(train_set), epoch)

        # 添加所有参数
        for name, weight in network.named_parameters():
            tb.add_histogram(name, weight, epoch)
            tb.add_histogram(f'{name}.grad', weight.grad, epoch)

        print('epoch:', epoch, 'total_correct:', total_correct, 'loss:', total_loss)

    tb.close()

刷新tensorboard就可以看到新的输出。

Section 4：神经网络实验#

对应视频： $P_{32}\sim P_{39}$

P32：编写Run Builder类，使不同的参数值生成多个运行

from collections import OrderedDict
from collections import namedtuple
from itertools import product

# 能让我们在训练过程中尝试不同的值时，拥有更大的控制能力
class RunBuilder():
    @staticmethod # 这意味着我们不需要类的实例来调用该方法
    def get_runs(params):
        Run = namedtuple('Run', params.keys())

        runs = []
        for v in product(*params.values()): # product函数给了一组定义我们运行的顺序对
            runs.append(Run(*v)) # 为每一个都添加一个运行列表

        return runs

RunBuilder的运行：

# 如何构建
params = OrderedDict(
    lr = [.01, 0.001]
    ,batch_size = [1000, 10000]
)

runs = RunBuilder.get_runs(params)
runs

输出：

[Run(lr=0.01, batch_size=1000),
 Run(lr=0.01, batch_size=10000),
 Run(lr=0.001, batch_size=1000),
 Run(lr=0.001, batch_size=10000)]

可以看到RunBuilder已经构建并返回了一个四次运行的列表。

如果我们将额外的值添加到测试中，就是将它们添加到原始的参数列表中。如果想要添加一个全新的参数，新参数将自动在运行中被使用，运行输出的字符串也会更新。下图展示了添加新参数后的运行效果：

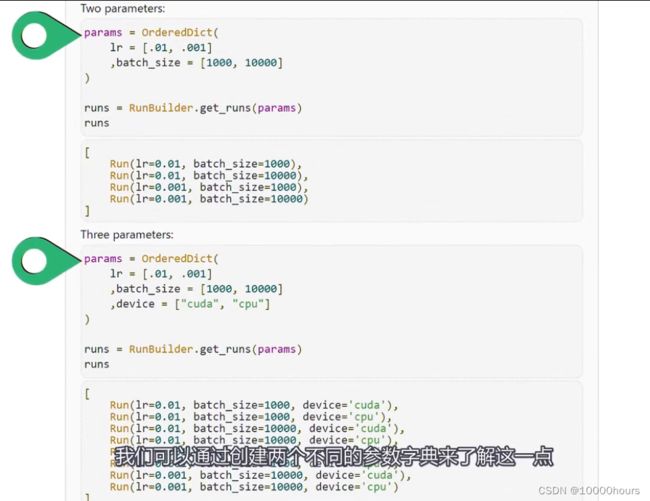
通过这个方法，我们就可以将之前的这种代码：

for lr batch_size, shuffle in product(*param_values):
	comment = f'batch_size={batch_size} lr={lr} shuffle={shuffle}'
	# 给定参数集的训练过程

修改为以下代码：

for fun in RunBuilder.get_runs(params):
	comment = f'-{run}'
	# 给定参数集的训练过程

P33：同步超参数测试

在本节中将演示如何轻松地实验大量的超参数值，同时保持训练循环和结果。

我们的目标是能够在顶部添加参数和值，并在多次训练中测试或尝试这些值。另外，我们希望能够添加任意数量的参数和任意数量的参数值，并仍然能推断出结果和组成循环训练的代码，为此我们需要新建类：RunBuilder（上节已经构建），RunManager（它允许我们管理运行循环中的每个运行）。

构建RunManager：

class RunManager():
    def __init__(self):

        self.epoch_count = 0
        self.epoch_loss = 0
        self.epoch_num_correct = 0
        self.epoch_start_time =  None

        self.run_params = None
        self.run_count = 0
        self.run_data = []
        self.run_start_time = None

        self.network = None
        self.loader = None
        self.tb = None

    def begin_run(self, run, network, loader):

        self.run_start_time = time.time()

        self.run_params = run
        self.run_count += 1

        self.network = network
        self.loader = loader
        self.tb = SummaryWriter(comment=f'-{run}')

        images, labels = next(iter(self.loader))
        grid = torchvision.utils.make_grid(images)

        self.tb.add_image('images',grid)
        self.tb.add_graph(self.network, images)

    def end_run(self):
        self.tb.close()
        self.epoch_count = 0

    def begin_epoch(self):
        self.epoch_start_time = time.time()

        self.epoch_count += 1
        self.epoch_loss = 0
        self.epoch_num_correct = 0

    def end_epoch(self):
        epoch_duration = time.time() - self.epoch_start_time
        run_duration = time.time() - self.run_start_time

        loss = self.epoch_loss / len(self.loader.dataset)
        accuracy = self.epoch_num_correct / len(self.loader.dataset)

        self.tb.add_scalar('Loss', loss, self.epoch_count)
        self.tb.add_scalar('Accuracy', accuracy, self.epoch_count)

        for name, param in self.network.named_parameters():
            self.tb.add_histogram(name, param, self.epoch_count)
            self.tb.add_histogram(f'{name}.grad', param.grad, self.epoch_count)

        results = OrderedDict()
        results['run'] = self.run_count
        results['epoch'] = self.epoch_count
        results['loss'] = loss
        results['accuracy'] = accuracy
        results['epoch duration'] = epoch_duration
        results['run duration'] = run_duration
        for k,v in self.run_params._asdict().items(): results[k] = v
        self.run_data.append(results)
        df = pd.DataFrame.from_dict(self.run_data, orient='columns')

        # 如果在Jupyter notebook中运行，加上下面两句
        from IPython.display import clear_output # 提醒我clear_out没定义,于是我import了一下
        clear_output(wait=True)
        display(df)

    def track_loss(self, loss):
        self.epoch_loss += loss.item() * self.loader.batch_size

    def track_num_correct(self, preds, labels):
        self.epoch_num_correct += self._get_num_correct(preds, labels)

    @torch.no_grad()
    def _get_num_correct(self, preds, labels):
        return preds.argmax(dim=1).eq(labels).sum().item()

    def save(self, fileName):
        pd.DataFrame.from_dict(
            self.run_data
            ,orient='columns'
        ).to_csv(f'{fileName}.csv')

        import json
        with open(f'{fileName}.json', 'w', encoding='utf-8') as f:
            json.dump(self.run_data, f, ensure_ascii=False, indent=4)

测试运行一下：

params = OrderedDict(
    lr = [.01, 0.001]
    ,batch_size = [1000, 10000]
    ,shuffle = [True, False]
)

m = RunManager()
for run in RunBuilder.get_runs(params):
    network = Network()
    loader = torch.utils.data.DataLoader(train_set, batch_size=run.batch_size, shuffle=run.shuffle)
    optimizer = optim.Adam(network.parameters(), lr=run.lr)
    
    m.begin_run(run, network, loader)
    for epoch in range(5):
        m.begin_epoch()
        for batch in loader:
            
            images = batch[0]
            labels = batch[1]
            preds = network(images)
            loss = F.cross_entropy(preds, labels)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            m.track_loss(loss)
            m.track_num_correct(preds, labels)
            
        m.end_epoch()
    m.end_run()
m.save('results')

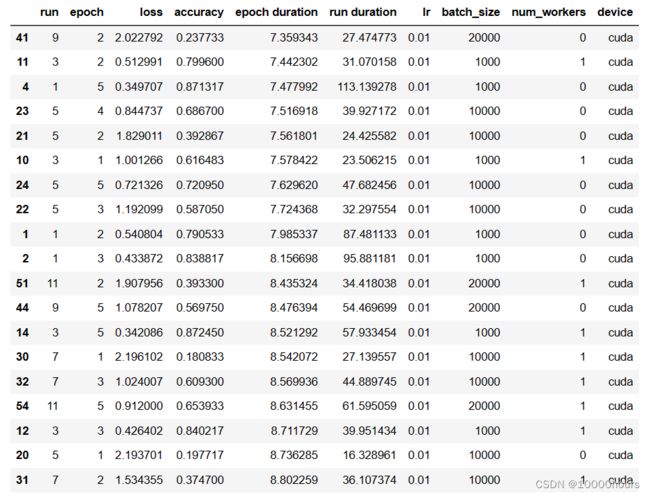
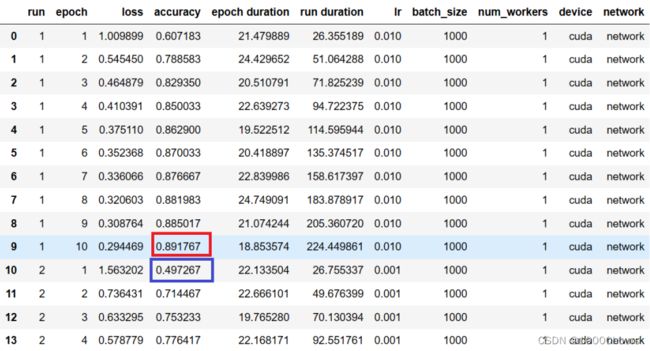
输出结果如下图所示。我们可以看到不同参数设置下的不同loss和accuracy值，由此能便于我们做进一步的分析。

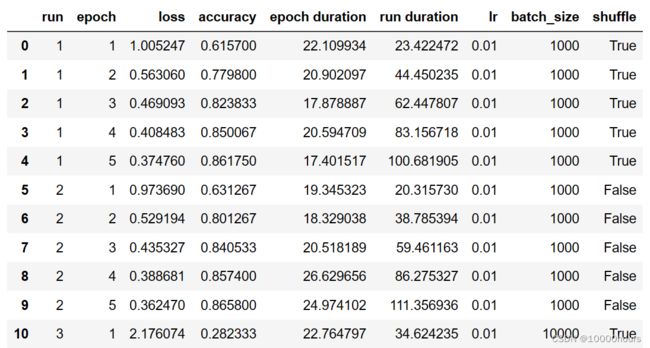
P34：加速神经网络训练过程

num_worker告诉数据加载器有多少子进程用于数据加载，它的值通常为0，表明在主进程中加载数据，表明训练过程将按顺序进行。

如何知道应该添加多少个工作进程（num_worker=?）？最好是测试：

params = OrderedDict(
    lr = [.01,]
    ,batch_size = [1000, 10000]
    , num_workers = [0, 1, 2, 4, 8, 16]
    #,shuffle = [True, False]
)

m = RunManager()
for run in RunBuilder.get_runs(params):
    network = Network()
    loader = torch.utils.data.DataLoader(train_set, batch_size=run.batch_size,num_workers=run.num_workers)
    optimizer = optim.Adam(network.parameters(), lr=run.lr)
    
    m.begin_run(run, network, loader)
    for epoch in range(5):
        m.begin_epoch()
        for batch in loader:
            
            images = batch[0]
            labels = batch[1]
            preds = network(images)
            loss = F.cross_entropy(preds, labels)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            m.track_loss(loss)
            m.track_num_correct(preds, labels)
            
        m.end_epoch()
    m.end_run()
m.save('results')

查看输出结果：
当num_worker从0增加到1时，可以看到epoch duration和run duration都有一定程度的减小：

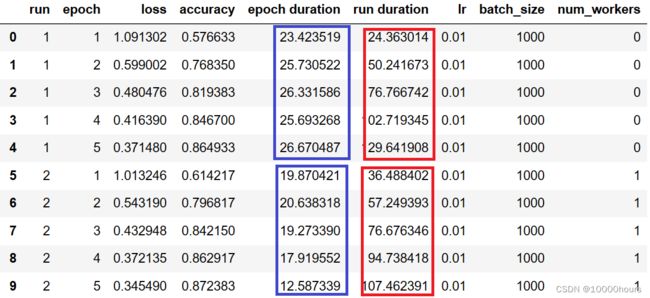
增加到2效果也较为明显，然而继续增加到4，epoch duration和run duration竟增加了，从4到8变化也不大：

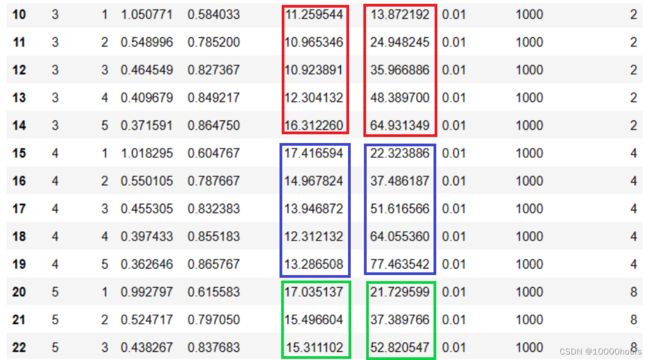
当增加到16时，直接出现错误（如下图所示）。出现死锁，导致程序卡住，线程阻塞：

可见num_worker的值并非越大越好，需要仔细斟酌后再设定。

P35：使用 CUDA 训练神经网络

tensor with CUDA

定义张量t1和t2之后，它们的默认计算设备为CPU，使用.to('cuda')可以将计算设备换成GPU，此时t1的计算设备就是GPU了：

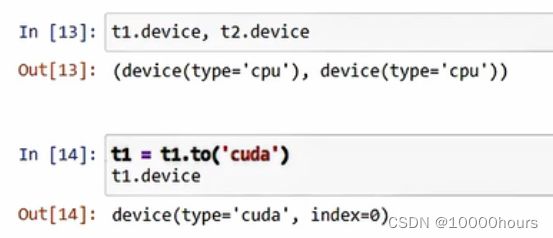
此时，若让两个位于不同计算设备的张量进行计算，会出现下面这样的问题。可以看出，机器希望参与运算的第二个参数拥有与第一个参数相同的计算设备：

将二者的计算设备都改为’cuda’，计算可以顺利执行：

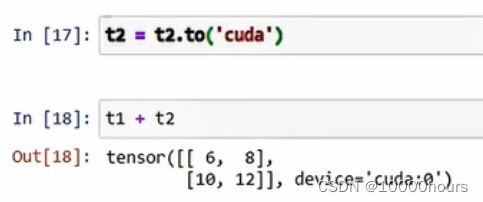
network with CUDA

定义一个网络，输出其参数，以及所在的计算设备：

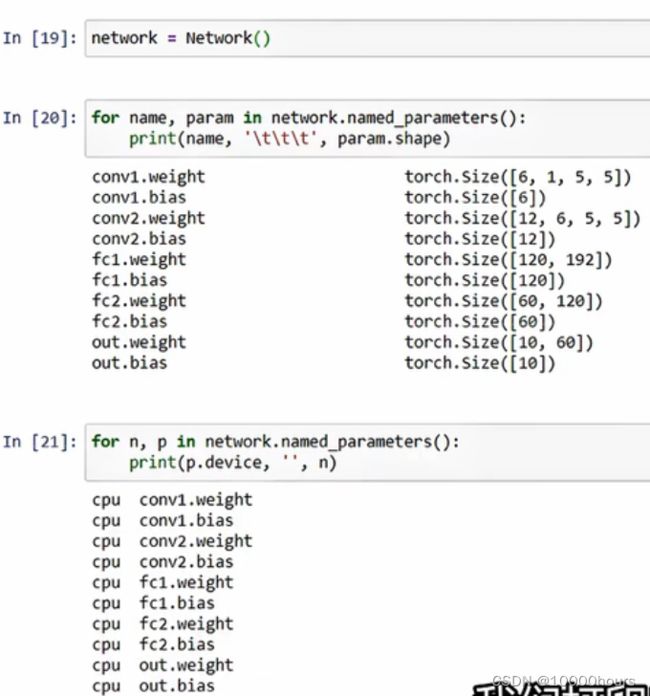
这说明在默认情况下，当我们创建一个pytorch网络，它的所有参数都是在CPU上初始化的。

将网络移动到GPU上：

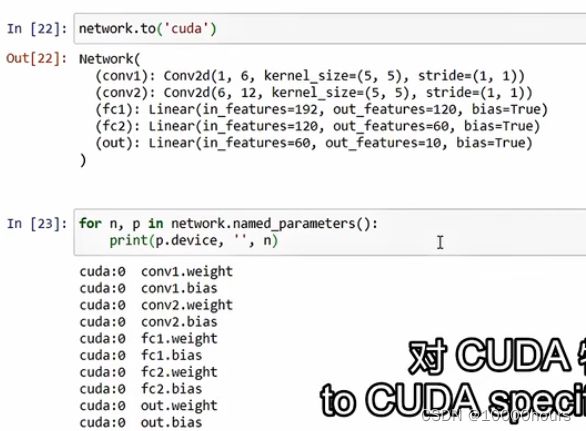
创建一个样本，并将该样本传递给网络（样本在CPU上初始化）捕捉到异常：

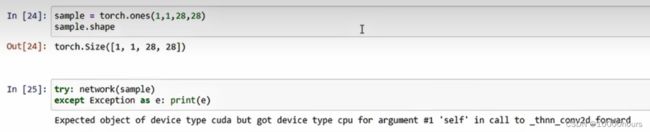
将样本移动到CUDA之后，可以正常计算：

检测系统中CUDA能否使用

可以用以下语句检测：

torch.cuda.is_available()

GPU vs CPU

测试GPU到底加速多少?
首先修改RunManager的begin_run方法：

然后执行以下测试代码：

params = OrderedDict(
    lr = [.01,]
    , batch_size = [1000, 10000, 20000]
    , num_workers = [0, 1]
    , device = ['cuda', 'cpu']
)

m = RunManager()
for run in RunBuilder.get_runs(params):
    
    # device 
    device = torch.device(run.device)    
    network = Network().to(device)
    
    loader = torch.utils.data.DataLoader(train_set, batch_size=run.batch_size,num_workers=run.num_workers)
    optimizer = optim.Adam(network.parameters(), lr=run.lr)
    
    m.begin_run(run, network, loader)
    for epoch in range(5):
        m.begin_epoch()
        for batch in loader:
            
            # to device
            images = batch[0].to(device)
            labels = batch[1].to(device)
            
            preds = network(images)
            loss = F.cross_entropy(preds, labels)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            m.track_loss(loss)
            m.track_num_correct(preds, labels)
            
        m.end_epoch()
    m.end_run()
m.save('results')

可以看到输出结果：
然后将输出结果按epoch duration排序：

# 排序
pd.DataFrame.from_dict(m.run_data, orient='columns').sort_values('epoch duration')

可以看到cuda遥遥领先：

P36：数据集规范化

均值和标准差

先创建数据集：

# 数据集规范化
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms

from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
        # normalize
    ])
)

先用一种简单的方式计算数据集的均值和标准差：

# easy way
loader = DataLoader(train_set, batch_size=len(train_set),num_workers=1)
data = next(iter(loader))
data[0].mean(), data[0].std()

输出

(tensor(0.2860), tensor(0.3530))

另一种方式：

# harder way
# 迭代多批数据。如果数据太大，我们将其分解为多个批次处理
loader = DataLoader(train_set, batch_size=1000, num_workers=1)
num_of_pixels = len(train_set) * 28 * 28 # 图像中总像素数

total_sum = 0
for batch in loader : total_sum += batch[0].sum()
mean = total_sum / num_of_pixels

sum_of_squared_error = 0
for batch in loader : sum_of_squared_error += ((batch[0] - mean).pow(2)).sum()
std = torch.sqrt(sum_of_squared_error / num_of_pixels)
    
mean, std

输出：

(tensor(0.2860), tensor(0.3530))

可以看到两种方式下的结果是相同的。

数据的直方图如下，中间的竖线就是其均值：

归一化和不归一化的效果区别

创建一个归一化的数据集：

# 使用均值和方差
train_set_normal = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
        , transforms.Normalize(mean, std)
    ])
)

查看数据集的均值和标准差：

loader = DataLoader(train_set_normal, batch_size=len(train_set),num_workers=1)
data = next(iter(loader))
data[0].mean(), data[0].std()

输出：

(tensor(-9.3670e-08), tensor(1.))

可以看到均值为0，标准差为1，这是归一化的结果。

测试归一化和不归一化的训练效果：

trainsets = {
    'not_normal' : train_set
    , 'normal' : train_set_normal
}

params = OrderedDict(
    lr = [.01]
    ,batch_size = [1000]
    ,num_workers = [1]
    , device = ['cuda']
    , trainset = ['not_normal', 'normal']
)

m = RunManager()
for run in RunBuilder.get_runs(params):
    
    device = torch.device(run.device)    
    network = Network().to(device)    
    loader = torch.utils.data.DataLoader(trainsets[run.trainset], batch_size=run.batch_size,num_workers=run.num_workers)
    optimizer = optim.Adam(network.parameters(), lr=run.lr)
    
    m.begin_run(run, network, loader)
    for epoch in range(10):
        m.begin_epoch()
        for batch in loader:
            
            images = batch[0].to(device)
            labels = batch[1].to(device)            
            preds = network(images)
            loss = F.cross_entropy(preds, labels)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            m.track_loss(loss)
            m.track_num_correct(preds, labels)
            
        m.end_epoch()
    m.end_run()
m.save('results')

得到的运行结果如下：

按照accuracy对结果进行排序：

pd.DataFrame.from_dict(m.run_data).sort_values('accuracy',ascending=False)

可以看到归一化有利于得到更高的精确度。但是并非每次都要归一化，要针对不同的数据做相应的处理。

P37：调试PyTorch 数据加载器源代码

略。

P38：使用Sequential类来建立神经网络的顺序

准备工作

import torch
import torch.nn as nn
import torch.nn.functional as F

import torchvision
import torchvision.transforms as transforms

import matplotlib.pyplot as plt
import math

from collections import OrderedDict

torch.set_printoptions(linewidth=150)

train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)

image, label = train_set[0] # image.shape:torch.Size([1, 28, 28])

in_features = image.numel() # 784
out_features = math.floor(in_features / 2) # 392
out_classes = len(train_set.classes) # 10

建立神经网络的顺序

方式一

network1 = nn.Sequential(
    nn.Flatten(start_dim=1)
    , nn.Linear(in_features, out_features)
    , nn.Linear(out_features, out_classes)
)

network1

输出：

Sequential(
  (0): Flatten(start_dim=1, end_dim=-1)
  (1): Linear(in_features=784, out_features=392, bias=True)
  (2): Linear(in_features=392, out_features=10, bias=True)
)

预测iamge：

image = image.unsqueeze(0)
network1(image)

输出：(这些是每个类别的10个预测，这个预测不够准确，因为我们还没有训练网络)

tensor([[-0.1980, -0.0317,  0.2527,  0.2140, -0.0549, -0.0994, -0.0038, -0.1374,  0.1117,  0.1083]], grad_fn=)

方式二

layers = OrderedDict([
    ('flat', nn.Flatten(start_dim=1))
    ,('hidden', nn.Linear(in_features, out_features))
    ,('output', nn.Linear(out_features, out_classes))          
])

network2 = nn.Sequential(layers)
network2

输出：

Sequential(
  (flat): Flatten(start_dim=1, end_dim=-1)
  (hidden): Linear(in_features=784, out_features=392, bias=True)
  (output): Linear(in_features=392, out_features=10, bias=True)
)

预测image：

network2(image)

输出：(预测结果不同。虽然network1和network2有着相同的结构，但是两个网络中的权重不同)

tensor([[-0.1359,  0.2879, -0.3738,  0.0343, -0.0800,  0.2685,  0.5197,  0.0467, -0.0519,  0.1609]], grad_fn=)

若想要这两个网络得到相同的预测，需设置随机数种子：

torch.manual_seed(50)
network1 = nn.Sequential(
    nn.Flatten(start_dim=1)
    , nn.Linear(in_features, out_features)
    , nn.Linear(out_features, out_classes)
)

torch.manual_seed(50)
layers = OrderedDict([
    ('flat', nn.Flatten(start_dim=1))
    ,('hidden', nn.Linear(in_features, out_features))
    ,('output', nn.Linear(out_features, out_classes))          
])
network2 = nn.Sequential(layers)

network1(image), network2(image)

输出：(这次的预测是相同的)

(tensor([[ 0.1681,  0.1028, -0.0790, -0.0659, -0.2436,  0.1328, -0.0864,  0.0016,  0.1819, -0.0168]], grad_fn=),
 tensor([[ 0.1681,  0.1028, -0.0790, -0.0659, -0.2436,  0.1328, -0.0864,  0.0016,  0.1819, -0.0168]], grad_fn=))

方式三

torch.manual_seed(50)
network3 = nn.Sequential()
network3.add_module('flat', nn.Flatten(start_dim=1))
network3.add_module('hidden', nn.Linear(in_features, out_features))
network3.add_module('output', nn.Linear(out_features, out_classes)) 
network3

输出：

Sequential(
  (flat): Flatten(start_dim=1, end_dim=-1)
  (hidden): Linear(in_features=784, out_features=392, bias=True)
  (output): Linear(in_features=392, out_features=10, bias=True)
)

使用随机数种子后，3个网络的预测是一致的：

network1(image), network2(image), network3(image)

(tensor([[ 0.1681,  0.1028, -0.0790, -0.0659, -0.2436,  0.1328, -0.0864,  0.0016,  0.1819, -0.0168]], grad_fn=),
 tensor([[ 0.1681,  0.1028, -0.0790, -0.0659, -0.2436,  0.1328, -0.0864,  0.0016,  0.1819, -0.0168]], grad_fn=),
 tensor([[ 0.1681,  0.1028, -0.0790, -0.0659, -0.2436,  0.1328, -0.0864,  0.0016,  0.1819, -0.0168]], grad_fn=))

使用Sequential类建一个Network类

原始Network

class Network(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)

        self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
        self.fc2 = nn.Linear(in_features=120, out_features=60)
        self.out = nn.Linear(in_features=60, out_features=10)

    def forward(self, t):
        t = F.relu(self.conv1(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = F.relu(self.conv2(t))
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        t = t.reshape(-1, 12 * 4 * 4)
        t = F.relu(self.fc1(t))

        t = F.relu(self.fc2(t))

        t = self.out(t)

        return t

创建网络实例：

torch.manual_seed(50)
network = Network()

方式一

torch.manual_seed(50)
sequential1 = nn.Sequential(
    nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
    ,nn.ReLU()
    ,nn.MaxPool2d(kernel_size=2, stride=2)
    ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
    ,nn.ReLU()
    ,nn.MaxPool2d(kernel_size=2, stride=2)
    ,nn.Flatten(start_dim=1)
    ,nn.Linear(in_features=12 * 4 * 4, out_features=120)
    ,nn.ReLU()
    ,nn.Linear(in_features=120, out_features=60)
    ,nn.ReLU()
    ,nn.Linear(in_features=60, out_features=10)
)
sequential1

输出：

Sequential(
  (0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (1): ReLU()
  (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (3): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
  (4): ReLU()
  (5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (6): Flatten(start_dim=1, end_dim=-1)
  (7): Linear(in_features=192, out_features=120, bias=True)
  (8): ReLU()
  (9): Linear(in_features=120, out_features=60, bias=True)
  (10): ReLU()
  (11): Linear(in_features=60, out_features=10, bias=True)
)

方式二

torch.manual_seed(50)
layers = OrderedDict([
    ('conv1',nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5))
    ,('relu1', nn.ReLU())
    ,('maxpool1', nn.MaxPool2d(kernel_size=2, stride=2))
    
    ,('conv2', nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5))
    ,('relu2', nn.ReLU())
    ,('maxpool2', nn.MaxPool2d(kernel_size=2, stride=2))
    
    ,('flatten', nn.Flatten(start_dim=1))
    ,('fc1', nn.Linear(in_features=12 * 4 * 4, out_features=120))
    ,('relu3', nn.ReLU())
    
    ,('fc2', nn.Linear(in_features=120, out_features=60))
    ,('relu4', nn.ReLU())
    ,('out', nn.Linear(in_features=60, out_features=10))
])
sequential2 = nn.Sequential(layers)
sequential2

输出：

Sequential(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (relu1): ReLU()
  (maxpool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
  (relu2): ReLU()
  (maxpool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (fc1): Linear(in_features=192, out_features=120, bias=True)
  (relu3): ReLU()
  (fc2): Linear(in_features=120, out_features=60, bias=True)
  (relu4): ReLU()
  (out): Linear(in_features=60, out_features=10, bias=True)
)

方式三

方式三就是add_module，不再赘述

预测image

network(image), sequential1(image), sequential2(image)

输出：（因为使用了随机数种子，所以预测结果相同）

(tensor([[-0.0957,  0.1053, -0.1055,  0.1547, -0.0366, -0.0132,  0.0749, -0.1152,  0.0426,  0.0639]], grad_fn=),
 tensor([[-0.0957,  0.1053, -0.1055,  0.1547, -0.0366, -0.0132,  0.0749, -0.1152,  0.0426,  0.0639]], grad_fn=),
 tensor([[-0.0957,  0.1053, -0.1055,  0.1547, -0.0366, -0.0132,  0.0749, -0.1152,  0.0426,  0.0639]], grad_fn=))

P39：PyTorch 中的批处理规范

创建网络

torch.manual_seed(50)
network1 = nn.Sequential(
    nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
    ,nn.ReLU()
    ,nn.MaxPool2d(kernel_size=2, stride=2)
    ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
    ,nn.ReLU()
    ,nn.MaxPool2d(kernel_size=2, stride=2)
    ,nn.Flatten(start_dim=1)
    ,nn.Linear(in_features=12 * 4 * 4, out_features=120)
    ,nn.ReLU()
    ,nn.Linear(in_features=120, out_features=60)
    ,nn.ReLU()
    ,nn.Linear(in_features=60, out_features=10)
)
# 添加nn.BatchNorm2d()和nn.BatchNorm1d
torch.manual_seed(50)
network2 = nn.Sequential(
    nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
    ,nn.ReLU()
    ,nn.MaxPool2d(kernel_size=2, stride=2)
    ,nn.BatchNorm2d(6) # 6是因为out_channels=6
    ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
    ,nn.ReLU()
    ,nn.MaxPool2d(kernel_size=2, stride=2)
    ,nn.Flatten(start_dim=1)
    ,nn.Linear(in_features=12 * 4 * 4, out_features=120)
    ,nn.ReLU()
    ,nn.BatchNorm1d(120) # 120是因为out_features=120
    ,nn.Linear(in_features=120, out_features=60)
    ,nn.ReLU()
    ,nn.Linear(in_features=60, out_features=10)
)

准备数据

# train_set
train_set = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
    ])
)
loader = DataLoader(train_set, batch_size=len(train_set),num_workers=1)
data = next(iter(loader))
mean = data[0].mean()
std = data[0].std()

train_set_normal = torchvision.datasets.FashionMNIST(
    root='./data/FashionMNIST'
    ,train=True
    ,download=True
    ,transform=transforms.Compose([
        transforms.ToTensor()
        , transforms.Normalize(mean, std)
    ])
)

trainsets = {
    'not_normal' : train_set
    , 'normal' : train_set_normal
}

networks = {
    'no_batch_norm':network1
    ,'batch_norm':network2
}

测试

params = OrderedDict(
    lr = [.01]
    ,batch_size = [1000]
    ,num_workers = [1]
    , device = ['cuda']
    , trainset = ['normal']
    , network = list(networks.keys())
)

m = RunManager()
for run in RunBuilder.get_runs(params):
    
    device = torch.device(run.device)    
    network = networks[run.network].to(device)
    loader = torch.utils.data.DataLoader(trainsets[run.trainset], batch_size=run.batch_size,num_workers=run.num_workers)
    optimizer = optim.Adam(network.parameters(), lr=run.lr)
    
    m.begin_run(run, network, loader)
    for epoch in range(20):
        m.begin_epoch()
        for batch in loader:
            
            images = batch[0].to(device)
            labels = batch[1].to(device)            
            preds = network(images)
            loss = F.cross_entropy(preds, labels)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            m.track_loss(loss)
            m.track_num_correct(preds, labels)
            
        m.end_epoch()
    m.end_run()
m.save('results')

将测试结果排序：

pd.DataFrame.from_dict(m.run_data).sort_values('accuracy',ascending=False)

排序后的结果为：

可以看到batch_norm的网络的准确率达到了93.5%（最高），no_batch_norm的网络的准确率达到了91.4%（最高）。batch_norm 的网络能更快收敛。

Section 5：补充学习

对应视频： $P_{40}\sim P_{43}$

P40：重置reset网络的权重

重置单个层的权重

torch.manual_seed(50)
layer = nn.Linear(2,1) # 创建一个最基本的线性层

查看这个层的权重：

layer.weight

输出：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

更新权重：

t = torch.rand(2)
o = layer(t)
o.backward()

optimizer = optim.Adam(layer.parameters(), lr=0.01)
optimizer.step()

再次查看layer.weight，可以看到权重已经更新：

Parameter containing:
tensor([[ 0.1569, -0.6200]], requires_grad=True)

重置layer的权重：

torch.manual_seed(50)
layer.reset_parameters()

再次查看layer.weight，可以看到已经恢复到最初的权重了：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

重置网络中的层的权重

all weights layer by layer

创建一个网络：

network = nn.Sequential(nn.Linear(2,1))

查看network[0].weight：

Parameter containing:
tensor([[-0.6500, -0.1395]], requires_grad=True)

采用for循环重置网络内层的权重：

torch.manual_seed(50)
for module in network.children():
    module.reset_parameters()

查看network[0].weight，可以看到network[0]的权重成功重置：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

为网络增加一层：

# 增加一层
network = nn.Sequential(
    nn.Linear(2,1)
    ,nn.Softmax()
)
network

Sequential(
  (0): Linear(in_features=2, out_features=1, bias=True)
  (1): Softmax(dim=None)
)

再次使用for循环重置网络内层的权重：

try:
    torch.manual_seed(50)
    for module in network.children():
        module.reset_parameters()
except Exception as e:
    print(e)

这时会出现这种情况：

'Softmax' object has no attribute 'reset_parameters'

这是因为子层可能没有参数，因此仅采用for循环重置每一层的参数是有风险的。

all weights using snapshot

snapshot 是一种灵活重置的方式。

创建网络：

torch.manual_seed(50)
network = nn.Sequential(nn.Linear(2,1))

查看network[0].weight：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

保存网络当前的状态：

torch.save(network.state_dict(), "./network.pt")

然后更新网络权重：

t = torch.rand(2)
o = network(t)
o.backward()

optimizer = optim.Adam(network.parameters(), lr=0.01)
optimizer.step()

此时再次查看network[0].weight，可以看到权重已经更新：

Parameter containing:
tensor([[ 0.1569, -0.6200]], requires_grad=True)

加载刚刚保存的网络状态：

network.load_state_dict(torch.load("./network.pt"))

然后再次查看network[0].weight：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

这种方式，可以在网络训练的任何时候保存权重，然后在想使用的时候加载出来。

all weights using re-initialization

创建网络：

torch.manual_seed(50)
network = nn.Sequential(nn.Linear(2,1))

查看network[0].weight：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

更新网络权重:

t = torch.rand(2)
o = network(t)
o.backward()

optimizer = optim.Adam(network.parameters(), lr=0.01)
optimizer.step()

再次查看network[0].weight，可以看到权重已更新：

Parameter containing:
tensor([[ 0.1569, -0.6200]], requires_grad=True)

然后重新初始化网络：

torch.manual_seed(50)
network = nn.Sequential(nn.Linear(2,1))

再次查看network[0].weight，可以看到权重已经恢复：

Parameter containing:
tensor([[ 0.1669, -0.6100]], requires_grad=True)

P41：改进测试框架

在之前的测试中，我们使用RunBuilder和RunManager类来测试不同的网络，但是每结束一个网络的测试并开始下一个新的网络的测试时，这个新网络的测试是以上一个旧网络测试的结束为起点的，如下图所示：（在run1到run2的过渡中，这测试的是两个不同的网络，但是accuracy的值却相差无几）

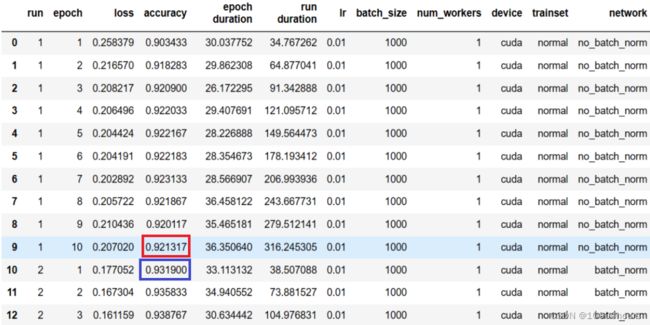
因此，在开始一个新网络的测试时，我们应重置网络的权重。为了达到该目的，写一个NetworkFacory类：

class NetworkFactory():
    @staticmethod
    def get_network(name):
        if name == 'network': # 重置网络权重
            torch.manual_seed(50)
            return  nn.Sequential(
                        nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
                        ,nn.ReLU()
                        ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
                        ,nn.ReLU()
                        ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Flatten(start_dim=1)
                        ,nn.Linear(in_features=12 * 4 * 4, out_features=120)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=120, out_features=60)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=60, out_features=10)
                    )
        else:
            return None

然后使用该类来进行测试：

params = OrderedDict(
    lr = [.01,.001]
    ,batch_size = [1000]
    ,num_workers = [1]
    , device = ['cuda']   
    , network = ['network']
)

m = RunManager()
for run in RunBuilder.get_runs(params):
    
    device = torch.device(run.device)    
    network = NetworkFactory.get_network(run.network).to(device)
    loader = torch.utils.data.DataLoader(train_set, batch_size=run.batch_size,num_workers=run.num_workers)
    optimizer = optim.Adam(network.parameters(), lr=run.lr)
    
    m.begin_run(run, network, loader)
    for epoch in range(10):
        m.begin_epoch()
        for batch in loader:
            
            images = batch[0].to(device)
            labels = batch[1].to(device)            
            preds = network(images)
            loss = F.cross_entropy(preds, labels)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            m.track_loss(loss)
            m.track_num_correct(preds, labels)
            
        m.end_epoch()
    m.end_run()
m.save('results')

测试结果如，可以看到这次run1向run2过渡时，两个网络的accuracy值就相差很大了，这是因为在测试新的网络时，进行了网络权重重置：

P42：Max Pooling vs No Max Pooling

网络如何在有和没有maxpooling的情况下执行。

修改NetworkFactory类：

class NetworkFactory():
    @staticmethod
    def get_network(name):
        if name == 'max_pool':
            torch.manual_seed(50)
            return  nn.Sequential(
                        nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
                        ,nn.ReLU()
                        ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
                        ,nn.ReLU()
                        ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Flatten(start_dim=1)
                        ,nn.Linear(in_features=12 * 4 * 4, out_features=120)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=120, out_features=60)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=60, out_features=10)
                    )
        elif name == 'no_max_pool':            
            torch.manual_seed(50)
            return  nn.Sequential(
                        nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
                        ,nn.ReLU()
#                         ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
                        ,nn.ReLU()
#                         ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Flatten(start_dim=1)
                        ,nn.Linear(in_features=12 * 20 * 20, out_features=120)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=120, out_features=60)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=60, out_features=10)
                    )

进行测试：

class NetworkFactory():
    @staticmethod
    def get_network(name):
        if name == 'max_pool':
            torch.manual_seed(50)
            return  nn.Sequential(
                        nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
                        ,nn.ReLU()
                        ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
                        ,nn.ReLU()
                        ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Flatten(start_dim=1)
                        ,nn.Linear(in_features=12 * 4 * 4, out_features=120)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=120, out_features=60)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=60, out_features=10)
                    )
        elif name == 'no_max_pool':            
            torch.manual_seed(50)
            return  nn.Sequential(
                        nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
                        ,nn.ReLU()
#                         ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
                        ,nn.ReLU()
#                         ,nn.MaxPool2d(kernel_size=2, stride=2)
                        ,nn.Flatten(start_dim=1)
                        ,nn.Linear(in_features=12 * 20 * 20, out_features=120)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=120, out_features=60)
                        ,nn.ReLU()
                        ,nn.Linear(in_features=60, out_features=10)
                    )

对测试结果按accuracy排序：

pd.DataFrame.from_dict(m.run_data).sort_values('accuracy',ascending=False)

结果如下：

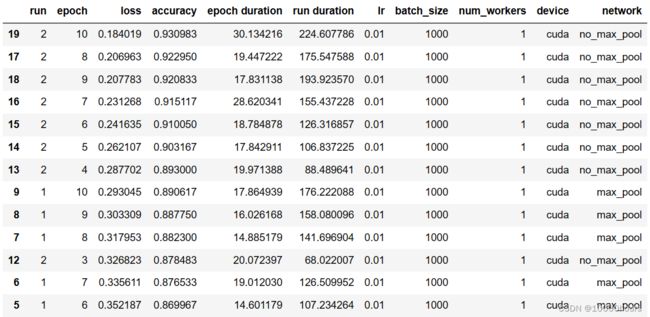
可以看到no_max_pool的精确度是更高的，这种结果的原因可能是，我们的数据已经足够简单，我们再maxpooling，实际上就会丢失很多数据。

可以看下面两个例子，左边是原始输入，右边是执行maxpooling操作后。

尽管右边的输出相对接近原始输入，但是丢失了太多数据，比如衬衫上的方块变成了右边的直线：

下面这张图就更明显了：

P43：结束课程

课程学习路线：

课程结束，借用授课老师最后说的话激励一下自己，以及每个看到这里的屏幕前的你：
No matter what you’re pursuing, it does not matter how slow you go, as long as you do not stop.

个人笔记第一部分：DeepLizard：Pytorch神经网络编程教学(第一部分)

你可能感兴趣的:(AI,Learning,pytorch,神经网络,深度学习)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
android系统selinux中添加新属性property 辉色投像
1.定位/android/system/sepolicy/private/property_contexts声明属性开头：persist.charge声明属性类型：u:object_r:system_prop:s0图12.定位到android/system/sepolicy/public/domain.te删除neverallow{domain-init}default_prop:property
C语言宏函数南林yan C语言 c语言
一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
c++ 的iostream 和 c++的stdio的区别和联系黄卷青灯77 c++算法开发语言 iostream stdio
在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
LocalDateTime 转 String igotyback java 开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码说私域人工智能小程序
摘要：本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合，阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇，提升了用户信任感、拓展了营销渠道，并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展，社区团购作为一种新兴的商业模式，在满足消费者日常需
每日一题——第八十九题互联网打工人no1 C语言程序设计每日一练 c语言
题目：在字符串中找到提取数字，并统计一共找到多少整数，a123xxyu23&8889，那么找到的整数为123，23，8889//思想：#include#include#includeintmain(){charstr[]="a123xxyu23&8889";intcount=0;intnum=0;//用于临时存放当前正在构建的整数。boolinNum=false;//用于标记当前是否正在读取一个整
每日一题——第八十一题互联网打工人no1 C语言程序设计每日一练 c语言
打印如下图案:#includeintmain(){inti,j;charch='A';for(i=1;i<5;i++,ch++){for(j=0;j<5-i;j++){printf("");//控制空格输出}for(j=1;j<2*i;j++)//条件j<2*i{printf("%c",ch);//控制字符输出}printf("\n");}return0;}
每日一题——第八十二题互联网打工人no1 C语言程序设计每日一练 c语言
题目：将一个控制台输入的字符串中的所有元音字母复制到另一字符串中#include#include#include#include#defineMAX_INPUT1024boolisVowel(charp);intmain(){charinput[MAX_INPUT];charoutput[MAX_INPUT];printf("请输入一串字符串：\n");fgets(input,sizeof(inp
每日一题——第八十三题互联网打工人no1 C语言程序设计每日一练 c语言
题目：将输入的整形数字输出,输出1990，输出"1990"#include#defineMAX_INPUT1024intmain(){intarrr_num[MAX_INPUT];intnum,i=0;printf("请输入一个数字：");scanf_s("%d",&num);while(num!=0){arrr_num[i++]=num%10;num/=10;}printf("\"");for(
git常用命令笔记咩酱-小羊 git 笔记
###用习惯了idea总是不记得git的一些常见命令，需要用到的时候总是担心旁边站了人~~~记个笔记@_@，告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"[email protected]"基本操作克隆远程仓库gitclone查看
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
利用LangChain的StackExchange组件实现智能问答系统 nseejrukjhad langchain microsoft 数据库 python
利用LangChain的StackExchange组件实现智能问答系统引言在当今的软件开发世界中，StackOverflow已经成为程序员解决问题的首选平台之一。而LangChain作为一个强大的AI应用开发框架，提供了StackExchange组件，使我们能够轻松地将StackOverflow的海量知识库集成到我们的应用中。本文将详细介绍如何使用LangChain的StackExchange组件
如何部分格式化提示模板:LangChain中的高级技巧 nseejrukjhad langchain java 服务器 python
标题:如何部分格式化提示模板:LangChain中的高级技巧内容:如何部分格式化提示模板:LangChain中的高级技巧引言在使用大型语言模型(LLM)时,提示工程是一个关键环节。LangChain提供了强大的提示模板功能,让我们能更灵活地构建和管理提示。本文将介绍LangChain中一个高级特性-部分格式化提示模板,这个技巧可以让你的提示管理更加高效和灵活。什么是部分格式化提示模板?部分格式化提
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
Faiss Tips：高效向量搜索与聚类的利器焦习娜Samantha
FaissTips：高效向量搜索与聚类的利器faiss_tipsSomeusefultipsforfaiss项目地址:https://gitcode.com/gh_mirrors/fa/faiss_tips项目介绍Faiss是由FacebookAIResearch开发的一个用于高效相似性搜索和密集向量聚类的库。它支持多种硬件平台，包括CPU和GPU，能够在海量数据集上实现快速的近似最近邻搜索（AN
【PG】常见数据库、表属性设置江无羡数据库
PG的常见属性配置方法数据库复制、备份相关表的复制标识单表操作批量表操作链接数据库复制、备份相关表的复制标识单表操作通过ALTER语句单独更改一张表的复制标识。ALTERTABLE[tablename]REPLICAIDENTITYFULL;批量表操作通过代码块的方式，对某个schema中的所有表一起更新其复制标识。SELECTtablename,CASErelreplidentWHEN'd'TH
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
每日一题——第八十八题互联网打工人no1 C语言程序设计每日一练 c语言
题目：输入一个9位的无符号整数，判断其是否有重复数字#include#include#includeintmain(){charnum_str[10];printf("请输入一个9位数的无符号数：");scanf_s("%9d",&num_str);if(strlen(num_str)!=9){printf("输入的不是一个9位无符号整数，请重新输入");}else{if(hasDuplicate
mac电脑命令行获取电量小米人er 我的博客 macos 命令行
在macOS上，有几个命令行工具可以用来获取电量信息，最常用的是pmset命令。你可以通过以下方式来查看电池状态和电量信息：查看电池状态：pmset-gbatt这个命令会返回类似下面的输出：Nowdrawingfrom'BatteryPower'-InternalBattery-0(id=1234567)95%;discharging;4:02remainingpresent:true输出中包括电
【Git】常见命令(仅笔记) 好想有猫猫 Git Linux学习笔记 git 笔记 elasticsearch linux c++
文章目录创建/初始化本地仓库添加本地仓库配置项提交文件查看仓库状态回退仓库查看日志分支删除文件暂存工作区代码远程仓库使用`.gitigore`文件让git不追踪一些文件标签创建/初始化本地仓库gitinit添加本地仓库配置项gitconfig-l#以列表形式显示配置项gitconfiguser.name"ljh"#配置user.namegitconfiguser.email"[email protected]
OPENAIGC开发者大赛企业组AI黑马奖 | AIGC数智传媒解决方案 RPA中国人工智能 AIGC 传媒
在第二届拯救者杯OPENAIGC开发者大赛中，涌现出一批技术突出、创意卓越的作品。为了让这些优秀项目被更多人看到，我们特意开设了优秀作品报道专栏，旨在展示其独特之处和开发者的精彩故事。无论您是技术专家还是爱好者，希望能带给您不一样的知识和启发。让我们一起探索AIGC的无限可能，见证科技与创意的完美融合！创未来AI应用赛-企业组AI黑马奖作品名称：AIGC数智传媒解决方案参赛团队：深圳市三象智能技术
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
你可能遗漏的一些C#/.NET/.NET Core知识点追逐时光者 C#.NET DotNetGuide编程指南 c#.net .netcore microsoft
前言在这个快速发展的技术世界中，时常会有一些重要的知识点、信息或细节被忽略或遗漏。《C#/.NET/.NETCore拾遗补漏》专栏我们将探讨一些可能被忽略或遗漏的重要知识点、信息或细节，以帮助大家更全面地了解这些技术栈的特性和发展方向。拾遗补漏GitHub开源地址https://github.com/YSGStudyHards/DotNetGuide/blob/main/docs/DotNet/D
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
python多线程程序设计之一 IT_Beijing_BIT #Python 程序设计语言 python
python多线程程序设计之一全局解释器锁线程APIsthreading.active_count()threading.current_thread()threading.excepthook(args,/)threading.get_native_id()threading.main_thread()threading.stack_size([size])线程对象成员函数构造器start/ru
python语法——三目运算符 HappyRocking python python 三目运算符
在java中，有三目运算符，如：intc=(a>b)?a:b表示c取两者中的较大值。但是在python，不能直接这样使用，估计是因为冒号在python有分行的关键作用。那么在python中，如何实现类似功能呢？可以使用ifelse语句，也是一行可以完成，格式为：aifbelsec表示如果b为True，则表达式等于a，否则等于c。如：c=(aif(a>b)elseb)同样是完成了取最大值的功能。
C语言代码练习（第十九天）小小框架 C语言 C语言重点练习 c语言
今日练习：52、有一个已经排好序的数组，要求输入一个数后，按原来排序的规律将它插入数组中53、输出"魔方阵"。所谓魔方阵是指它的每一行，每一列和对角线之和均相等。54、找出一个二维数组中的鞍点，即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点。有一个已经排好序的数组，要求输入一个数后，按原来排序的规律将它插入数组中运行代码intmain(){intarr[11]={1,3,9,12,15
Java实现的简单双向Map，支持重复Value superlxw1234 java 双向map
关键字：Java双向Map、DualHashBidiMap 有个需求，需要根据即时修改Map结构中的Value值，比如，将Map中所有value=V1的记录改成value=V2，key保持不变。数据量比较大，遍历Map性能太差，这就需要根据Value先找到Key，然后去修改。即：既要根据Key找Value，又要根据Value
PL/SQL触发器基础及例子百合不是茶 oracle数据库触发器 PL/SQL编程
触发器的简介; 触发器的定义就是说某个条件成立的时候，触发器里面所定义的语句就会被自动的执行。因此触发器不需要人为的去调用，也不能调用。触发器和过程函数类似过程函数必须要调用, 一个表中最多只能有12个触发器类型的,触发器和过程函数相似触发器不需要调用直接执行, 触发时间：指明触发器何时执行，该值可取： before：表示在数据库动作之前触发
[时空与探索]穿越时空的一些问题 comsci 问题
我们还没有进行过任何数学形式上的证明,仅仅是一个猜想..... 这个猜想就是; 任何有质量的物体(哪怕只有一微克)都不可能穿越时空,该物体强行穿越时空的时候,物体的质量会与时空粒子产生反应,物体会变成暗物质,也就是说,任何物体穿越时空会变成暗物质..(暗物质就我的理
easy ui datagrid上移下移一行商人shang js 上移下移 easyui datagrid
/** * 向上移动一行 * * @param dg * @param row */ function moveupRow(dg, row) { var datagrid = $(dg); var index = datagrid.datagrid("getRowIndex", row); if (isFirstRow(dg, row)) {
Java反射 oloz 反射
本人菜鸟，今天恰好有时间，写写博客，总结复习一下java反射方面的知识，欢迎大家探讨交流学习指教首先看看java中的Class package demo; public class ClassTest { /*先了解java中的Class*/ public static void main(String[] args) { //任何一个类都
springMVC 使用JSR-303 Validation验证杨白白 spring mvc
JSR-303是一个数据验证的规范，但是spring并没有对其进行实现，Hibernate Validator是实现了这一规范的，通过此这个实现来讲SpringMVC对JSR-303的支持。 JSR-303的校验是基于注解的，首先要把这些注解标记在需要验证的实体类的属性上或是其对应的get方法上。登录需要验证类 public class Login { @NotEmpty
log4j 香水浓 log4j
log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, HTML, DATABASE #log4j.rootCategory=DEBUG, STDOUT, DAILYFILE, ROLLINGFILE, HTML #console log4j.appender.STDOUT=org.apache.log4j.ConsoleAppender log4
使用ajax和history.pushState无刷新改变页面URL agevs jquery 框架 Ajax html5 chrome
表现如果你使用chrome或者firefox等浏览器访问本博客、github.com、plus.google.com等网站时，细心的你会发现页面之间的点击是通过ajax异步请求的，同时页面的URL发生了了改变。并且能够很好的支持浏览器前进和后退。是什么有这么强大的功能呢？ HTML5里引用了新的API，history.pushState和history.replaceState，就是通过
centos中文乱码 AILIKES centos OS ssh
一、CentOS系统访问 g.cn ，发现中文乱码。于是用以前的方式：yum -y install fonts-chinese CentOS系统安装后，还是不能显示中文字体。我使用 gedit 编辑源码，其中文注释也为乱码。后来，终于找到以下方法可以解决，需要两个中文支持的包： fonts-chinese-3.02-12.
触发器 baalwolf 触发器
触发器(trigger)：监视某种情况，并触发某种操作。触发器创建语法四要素：1.监视地点(table) 2.监视事件(insert/update/delete) 3.触发时间(after/before) 4.触发事件(insert/update/delete) 语法： create trigger triggerName after/before
JS正则表达式的i m g bijian1013 JavaScript 正则表达式
g:表示全局（global)模式，即模式将被应用于所有字符串，而非在发现第一个匹配项时立即停止。 i:表示不区分大小写（case-insensitive）模式，即在确定匹配项时忽略模式与字符串的大小写。 m:表示
HTML5模式和Hashbang模式 bijian1013 JavaScript AngularJS Hashbang模式 HTML5模式
我们可以用$locationProvider来配置$location服务（可以采用注入的方式，就像AngularJS中其他所有东西一样）。这里provider的两个参数很有意思，介绍如下。 html5Mode 一个布尔值，标识$location服务是否运行在HTML5模式下。 ha
[Maven学习笔记六]Maven生命周期 bit1129 maven
从mvn test的输出开始说起当我们在user-core中执行mvn test时，执行的输出如下： /software/devsoftware/jdk1.7.0_55/bin/java -Dmaven.home=/software/devsoftware/apache-maven-3.2.1 -Dclassworlds.conf=/software/devs
【Hadoop七】基于Yarn的Hadoop Map Reduce容错 bit1129 hadoop
运行于Yarn的Map Reduce作业，可能发生失败的点包括 Task Failure Application Master Failure Node Manager Failure Resource Manager Failure 1. Task Failure 任务执行过程中产生的异常和JVM的意外终止会汇报给Application Master。僵死的任务也会被A
记一次数据推送的异常解决端口解决 ronin47 记一次数据推送的异常解决
　　需求：从db获取数据然后推送到B 程序开发完成，上jboss,刚开始报了很多错，逐一解决，可最后显示连接不到数据库。机房的同事说可以ping 通。　　自已画了个图，逐一排除，把linux 防火墙　和　setenforce　设置最低。　　　service iptables stop
巧用视错觉-UI更有趣 brotherlamp UI ui视频 ui教程 ui自学 ui资料
我们每个人在生活中都曾感受过视错觉（optical illusion）的魅力。视错觉现象是双眼跟我们开的一个玩笑，而我们往往还心甘情愿地接受我们看到的假象。其实不止如此，视觉错现象的背后还有一个重要的科学原理——格式塔原理。格式塔原理解释了人们如何以视觉方式感觉物体，以及图像的结构，视角，大小等要素是如何影响我们的视觉的。在下面这篇文章中，我们首先会简单介绍一下格式塔原理中的基本概念，
线段树-poj1177-N个矩形求边长（离散化+扫描线） bylijinnan 数据结构算法线段树
package com.ljn.base; import java.util.Arrays; import java.util.Comparator; import java.util.Set; import java.util.TreeSet; /** * POJ 1177 (线段树+离散化+扫描线)，题目链接为http://poj.org/problem?id=1177
HTTP协议详解 chicony http协议
引言
Scala设计模式 chenchao051 设计模式 scala
Scala设计模式我的话：在国外网站上看到一篇文章，里面详细描述了很多设计模式，并且用Java及Scala两种语言描述，清晰的让我们看到各种常规的设计模式，在Scala中是如何在语言特性层面直接支持的。基于文章很nice，我利用今天的空闲时间将其翻译，希望大家能一起学习，讨论。翻译
安装mysql daizj mysql 安装
安装mysql (1)删除linux上已经安装的mysql相关库信息。rpm -e xxxxxxx --nodeps (强制删除) 执行命令rpm -qa |grep mysql 检查是否删除干净 (2)执行命令 rpm -i MySQL-server-5.5.31-2.el
HTTP状态码大全 dcj3sjt126com http状态码
完整的 HTTP 1.1规范说明书来自于RFC 2616，你可以在http://www.talentdigger.cn/home/link.php?url=d3d3LnJmYy1lZGl0b3Iub3JnLw%3D%3D在线查阅。HTTP 1.1的状态码被标记为新特性，因为许多浏览器只支持 HTTP 1.0。你应只把状态码发送给支持 HTTP 1.1的客户端，支持协议版本可以通过调用request
asihttprequest上传图片 dcj3sjt126com ASIHTTPRequest
NSURL *url =@"yourURL"; ASIFormDataRequest*currentRequest =[ASIFormDataRequest requestWithURL:url]; [currentRequest setPostFormat:ASIMultipartFormDataPostFormat];[currentRequest se
C语言中，关键字static的作用 e200702084 C++c C#
在C语言中，关键字static有三个明显的作用： 1)在函数体，局部的static变量。生存期为程序的整个生命周期，（它存活多长时间）；作用域却在函数体内（它在什么地方能被访问（空间））。一个被声明为静态的变量在这一函数被调用过程中维持其值不变。因为它分配在静态存储区，函数调用结束后并不释放单元，但是在其它的作用域的无法访问。当再次调用这个函数时，这个局部的静态变量还存活，而且用在它的访
win7/8使用curl geeksun win7
1. WIN7/8下要使用curl，需要下载curl-7.20.0-win64-ssl-sspi.zip和Win64OpenSSL_Light-1_0_2d.exe。下载地址： http://curl.haxx.se/download.html 请选择不带SSL的版本，否则还需要安装SSL的支持包 2. 可以给Windows增加c
Creating a Shared Repository; Users Sharing The Repository hongtoushizi git
转载自： http://www.gitguys.com/topics/creating-a-shared-repository-users-sharing-the-repository/ Commands discussed in this section: git init –bare git clone git remote git pull git p
Java实现字符串反转的8种或9种方法 Josh_Persistence 异或反转递归反转二分交换反转 java字符串反转栈反转
注：对于第7种使用异或的方式来实现字符串的反转，如果不太看得明白的，可以参照另一篇博客： http://josh-persistence.iteye.com/blog/2205768 /** * */ package com.wsheng.aggregator.algorithm.string; import java.util.Stack; /**
代码实现任意容量倒水问题 home198979 PHP 算法倒水
形象化设计模式实战 HELLO!架构 redis命令源码解析倒水问题：有两个杯子，一个A升，一个B升，水有无限多，现要求利用这两杯子装C
Druid datasource zhb8015 druid
推荐大家使用数据库连接池 DruidDataSource. http://code.alibabatech.com/wiki/display/Druid/DruidDataSource DruidDataSource经过阿里巴巴数百个应用一年多生产环境运行验证，稳定可靠。它最重要的特点是：监控、扩展和性能。下载和Maven配置看这里： http
两种启动监听器ApplicationListener和ServletContextListener spjich java spring 框架
引言:有时候需要在项目初始化的时候进行一系列工作，比如初始化一个线程池，初始化配置文件，初始化缓存等等，这时候就需要用到启动监听器，下面分别介绍一下两种常用的项目启动监听器 ServletContextListener 特点: 依赖于sevlet容器，需要配置web.xml 使用方法: public class StartListener implements
JavaScript Rounding Methods of the Math object 何不笑 JavaScript Math
The next group of methods has to do with rounding decimal values into integers. Three methods — Math.ceil(), Math.floor(), and Math.round() — handle rounding in differen

【DeepLizard】Pytorch神经网络编程学习笔记(第二部分)

文章目录

Section 1：数据和数据处理

P14：fashion-mnist数据集

P15：使用torchvision演示一种简单的提取、转换和加载流程(ETL)

ETL过程

使用PyTorch准备数据

PyTorch Dataset Class

PyTorch DataLoader Class

P16：使用DataSet和DataLoader

查看数据

访问训练集中的数据

PyTorch DataLoader：处理成批的数据

Section 2：神经网络和 PyTorch 设计

P17：构建PyTorch CNN

一些包和函数

构建神经网络

P18：CNN层，理解构建CNN时使用的参数

CNN层

CNN层参数

P19：CNN内部的权重张量

可学习参数

获取实例网络

访问层的权重

权重张量形状

权重矩阵

P20：PyTorch可调用的神经网络模块，以及网络和层的前向方法是如何调用的

Linear类中的权重

特殊的调用方法：__call()__函数

P21：调试PyTorch源代码

P22：实现一个卷积神经网络的前向方法

P23：使用卷积神经网络由数据集的样本输入生成输出预测答案

P24：将一批图像传递到网络并解释输出

P25：一个输入张量在通过CNN的过程中的变化

CNN输出尺寸公式（方形）

CNN输出尺寸公式（非方形）

Section 3：训练神经网络

P26：训练卷积神经网络（单个批次）

训练卷积神经网络所需的步骤

代码实现

P27：构建一个卷积神经网络的训练循环

P28：构建混淆矩阵

P29：拼接张量和堆叠张量

P30：使用tensorboard来可视化CNN在网络训练过程中的指标

P31：神经网络超参数

每次修改单个超参数值

循环遍历不同的超参数值

添加更多的参数

Section 4：神经网络实验#

P32：编写Run Builder类，使不同的参数值生成多个运行

P33：同步超参数测试

P34：加速神经网络训练过程

P35：使用 CUDA 训练神经网络

tensor with CUDA

network with CUDA

检测系统中CUDA能否使用

GPU vs CPU

P36：数据集规范化

均值和标准差

归一化和不归一化的效果区别

P37：调试PyTorch 数据加载器源代码

P38：使用Sequential类来建立神经网络的顺序

准备工作

建立神经网络的顺序

方式一

方式二

方式三

使用Sequential类建一个Network类

原始Network

方式一

方式二

方式三

预测image

P39：PyTorch 中的批处理规范

创建网络

准备数据

测试

Section 5：补充学习

P40：重置reset网络的权重

重置单个层的权重

特殊的调用方法：call()函数