高通量测序技术和序列拼接算法探析

　　摘    要：　高通量测序 (High-throughput Sequencing, HTS) 技术是继第一代测序技术之后发展起来的一种新型测序方式, 又被称为下一代测序技术。与第一代测序技术中采用基于Sanger方法的自动、半自动毛细管测序方法不同, 高通量测序技术采用了基于焦磷酸测序的并行测序技术, 是对传统测序技术的一项重要技术突破, 它不仅克服了第一代测序技术高成本、低通量、低速度的缺点, 而且能满足现代分子生物学和基因组学快速发展的需求, 达到低成本、高通量以及快速的目的。相较于第一代测序数据, 高通量测序数据具有典型的长度短、覆盖度不均匀以及准确率低的特点, 同时第三代测序技术虽保持了高通量测序技术边测序边合成的思想, 但采用了更为高效的单分子实时测序技术和纳米孔测序技术, 具有高通量、低成本和测序数据长的优势。因此, 要获得完整的全基因组基因序列, 生物学家就需要使用一种技术将短测序reads拼装成一条完整的基因单链序列。在这种情况下, 序列拼接算法应运而生。首先, 介绍了序列拼接算法的发展背景以及高通量测序技术的相关概念, 分析了高通量测序技术在序列拼接算法中所具有的优势;其次, 通过总结序列拼接算法的发展成果, 按基于greedy策略、基于Overlap-Layout-Consensus (OLC) 策略和基于De Bruijn Graph (DBG) 策略的分类对序列拼接算法进行阐述;最后, 探讨了序列拼接算法的相关研究方向和发展趋势。

　　关键词：　高通量测序技术; 序列拼接算法; greedy; Overlap-Layout-Consensus; De Bruijn Graph;

　　Abstract：　High-throughput sequencing technology is a new sequencing method developed after the first generation sequencing technology, also known as next-generation sequencing technology.Different from the automatic and semi-automatic capillary sequencing method based on Sanger, the high-throughput sequencing technology adopts the parallel sequencing technology based on pyrosequencing.It not only conquers the shortcomings of high cost, low throughput and low speed of the first generation sequencing technology, but also meets the demands of the rapid development of modern molecular biology and genomics with low cost, high throughput and fast speed.Compared with the first generation sequencing data, high-throughput sequencing data are characterized by short lengths, uneven coverage and low accuracy, and the third-generation sequencing technology adopts more efficient single molecular real-time sequencing and Nanopore sequencing technology as well as the principle of sequencing and synthesis, which has the advantages of high throughput, low cost and long sequencing data.Therefore, in order to obtain complete genome sequence, a technique is needed to assemble short sequencing reads into a complte single-stranded sequence of genes.In this case, the sequence assembly algorithm was proposed.Firstly, the development background of sequence assembly algorithms and the related concepts of high-throughput sequencing technology were introduced, and the advantages of high-throughput sequencing technology on sequence assembly were analyzed.Secondly, by summarizing the development of sequence assembly algorithms.The sequence assembly algorithms were illustrated, according to the algorithm classifications, respectively, by greedy strategy, Overlap-Layout-Consensus (OLC) strategy and De Bruijn Graph (DBG) strategy.Finally, the research direction and development trend of sequence assembly algorithms were discussed.

　　Keyword：　High-throughput sequencing; Sequence assembly algorithms; Greedy; Overlap-layout-consensus; De bruijn graph;

　　1、 引言

　　随着测序技术的发展, 生物学家获得了海量的生物测序数据, 这些测序数据被广泛应用于医学、遗传科学和生物学等诸多领域。为了通过分析这些测序数据来更多地了解生物之间的功能、结构和进化关系等生物学含义, 研究人员建立了大量的公共测序数据库, 如美国国家生物技术信息中心NCBI、欧洲生物信息研究所EBI、日本DNA数据库DDBJ, 从而有利于高效地整合、处理以及分析不同类型的测序数据, 使得人们可以通过互联网来更为方便地进行交流和研究, 保证资源和信息共享[1];同时, 大量的相似性比对工具[2,3,4,5,6]也被成功地用于解决同源性数据库搜索和高通量测序数据相似性比对问题。由于一些生物基因组全序列的成功测定, 人们可从整个基因组的规模来全面了解现有生物基因之间的功能和结构关系及差异, 同时能够清晰了解并研究导致生物病变的侯选基因, 进而促进生物基因科技的发展, 对生物学研究、探索与认识生物进化的本质提供重要参考, 为序列拼接算法的快速发展奠定基础。

　　高通量测序技术的发展使得研究人员能够以更高的效率来获得细菌、真菌乃至动植物的全基因组序列图谱, 加快了对相应物种基因的研究, 使得研究相近物种间的进化关系成为可能。在人类基因组计划[7]完成以来, 通过蛋白质序列测定、基因组测序和分子结构解析等试验, 千人基因组工程[8]和UK10K[9]成功地测序完成了上千人的基因组图谱, 且对单个人的测序花费降低至1 000美元以下[10]。然而, 高通量测序数据的膨胀式发展已然成为了现有计算条件下进行基因组测序的桎梏, 同时, 高通量测序数据存在测序reads短、重复率高以及覆盖度不均匀等不足。因此, 要获得生物的完整全基因组基因序列, 生物学家就需要使用一种技术将短测序reads拼装成一条完整的基因单链序列。在不断研究后, 生物学家发现可以使用计算机, 根据短测序reads间的重叠关系将这些reads数据拼接成一个或多个较长的序列片段, 最终获得生物的全基因组基因序列, 该拼接过程被称为序列拼接。因此, 研发一种针对超高量基因序列数据的基因组拼接组装技术是打破上述瓶颈的重要途径之一, 这也是人类全基因组序列研究的重要内容。

　　针对现有组装算法的研究与发展, 本文第2节简要介绍高通量测序技术的相关概念;第3节按基于greedy策略、基于OLC策略和基于DBG策略将序列拼接算法分成3类, 并阐述每类中具有代表性的算法;最后进行总结, 分析并探讨序列拼接组装算法研究中存在的问题和相关发展方向。

　　2、 高通量测序技术

　　高通量测序技术是在第一代测序技术基础上改进而来的一种新型基因组测序技术。第一代测序技术主要以基于Sanger[11]方法的自动、半自动毛细管测序技术为标志。在2003年, 科学家采用该技术完成了首个人类全基因组测序, 总共耗时3年并花费了4.37亿美元。为了解决第一代测序技术存在的成本高、通量低、速度低的缺点, 满足现代分子生物学和基因组学快速发展的需求, 达到低成本、高通量以及快速的目的, 454 Life Sciences公司于2005年开发了一种基于焦磷酸测序法的超高通量基因组测序系统, 其能够快速、准确地测定一段较短的DNA序列, 成为了第二代测序技术的开端。因此, 第二代基因组测序技术也被称为高通量测序技术或下一代测序技术。2007年, 科学家们首次使用高通量测序技术, 以耗时4个月和不到150万美元的花费完成了“DNA之父”詹姆斯·沃森的个人基因组测序。

　　随着HTS的发展, 所需拼接的基因组数据量也急速增长, 而且二代测序产生的reads较短 (30～500 bp) [12], 导致不仅HTS数据无法满足大多数序列分析的需要[13], 而且难以设计一种通用数据融合技术去处理高度不确定性、多源性和杂合度的基因组数据以及通过获取局部信息来反映全局问题[14]。为了应对该挑战, 越来越多的针对提高组装效率和适应不同测序序列数据的基因组拼接技术不断出现, 例如并行化拼接过程以及优化算法结构等。自2007年以来, 已经有70多个测序工具[15]尝试解决该问题。然而, 计算机的微处理性能和存储设备的容量平均每18～24个月增长一倍, 而基因组测序数据平均4～5个月就增长一倍, 因此延长测序序列长度和提升基因组组装算法效率成为了目前拼接庞大基因数据的重要方式。为了解决这一问题, 3GS (Third Generation Sequencing) 测序技术应运而生。3GS虽然保持了第二代测序技术的边合成边测序的思想[16], 但与第二代测序技术不同, 其在测序过程中使用了单分子荧光测序技术或纳米孔测序技术[17,18,19,20,21]。3GS在保证了原有高精度的情况下, 测序读长超过10 kB[22], 并且无需进行PCR扩增, 具有更快的测序速度和更低的测序成本, 为拼接基因组序列提供了便利。

　　HTS进行基因组测序时具有如下优势[23]:突破了一系列限制平行测序规模的瓶颈, 极大地提高了平行测序的能力;能够处理庞大的基因组序列, 具有高通量的特点;极大地降低了测序成本等。但是由于新一代测序技术的发展, 测序所产生的序列片段太短、覆盖度不均匀以及3GS产生的序列数据的错误率较高等问题, 不仅导致了在进行序列拼接组装的过程中需要进行大量计算, 而且降低了序列拼接组装的精确度。因此, 在现有计算能力大致不变的情况下, 学者们提出了一种新型的数据结构算法。该算法主要研究序列拼接算法的并行化问题, 以提高计算机的并行计算能力, 同时通过增加序列片段的长度来减小重复序列片段的影响, 从而极大地提高针对高通量测序技术所产生序列的组装速度和精确度, 并且已经产生了大量的融合二代数据和三代数据优势的拼接算法[24,25,26], 即利用“linked reads”来提高拼接的完整度。

　　3、 序列拼接算法

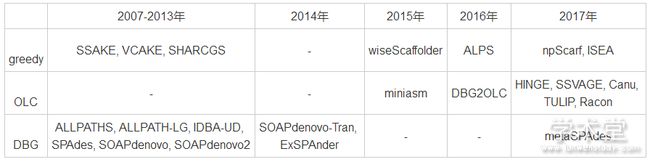
　　根据拼接策略的不同, 可以将序列拼接算法分为3种:基于greedy策略的算法、基于Overlap-Layout-Consensus策略的算法和基于De Bruijn Graph策略的算法。按照出版时间和拼接策略进行分类的结果如表1所列。

　　表1 主要序列拼接算法的分类

　　3.1、 基于greedy策略的拼接算法

　　Greedy策略是最早被应用于HTS拼接算法的策略。基于greedy策略的拼接算法首先通过一定的最优化规则来获取reads或contigs (重叠群) 作为初始种子序列, 然后基于这个种子序列向两边添加更多的reads或contigs, 延伸方案一般有基于最大重叠长度和投票机制两种[27], 直到reads或contigs无法再继续延伸为止, 最后重复上述过程, 直到所有序列拼接完成, 如图1所示。

　　图1 Greedy策略拼接示意图

　　Fig.1 Assembly graph based on greedy strategy

　　图1中, 在序列1的拼接过程中, 第一条待拼接序列和序列1在序列比对过程中有一个错配G (用深灰色表示, 下同) , 且有9个碱基匹配, 而下面的其他3条序列错配数分别为2, 3, 2, 匹配数分别为8, 5, 4, 因此将选取第一条进行拼接。但需要注意的是, 由于重复序列3 (浅灰色序列) 的影响, greedy策略可能会导致在实际拼接过程中序列1和序列4拼接在一起, 从而产生错误拼接, 进而影响拼接精确度。

　　在greedy策略中, reads或contigs的选取是按照碱基拼接质量递减的顺序来考虑的, 且该类算法能够应用于基于OLC策略以及DBG策略的拼接算法中。然而, 该类算法不仅容易陷入局部最优, 而且未充分考虑重复序列以及错误序列所造成的拼接歧义, 使得组装序列的错误率较高, 一般仅适用于小型基因组的拼接。其中比较经典的算法有SSAKE[28], VCAKE[29], SHARCGS[30], 这几种算法不显示使用拼接图, 而是基于重叠关系使用贪婪算法建立一致性序列。

　　wiseScaffolder[31]是一种建立在重叠群上并支持手工控制的迭代扩展策略。该算法把由paired-end reads拼接而成的重叠群与Meta-pair reads进行比对, 利用该比对信息检测出重叠群中的嵌合体位置并利用覆盖度估计重叠群拷贝数, 从而在嵌合体位置分割重叠群, 以消除嵌合体位置对序列拼接的影响。wiseScaffolder按照单拷贝重叠群长度从大到小的顺序进行两端扩展, 并利用比对信息将未参与scaffolding的重叠群插入到图中以消除空位。最后, 算法利用Meta-pair reads与拼接序列进行比对纠错, 以提高拼接序列的质量和完整度。

　　npScarf[32]是一种能在长reads测序过程中进行短reads序列拼接的迭代扩展算法。算法利用了Nanopore测序的实时特征, 首次实现了实时控制测序器的数据流并获得测序状态信息, 降低了过度测序的花费。算法利用重叠群拼接过程的覆盖度识别出独立重叠群, 然后找出同时与两个独立重叠群重叠且得分最大的reads用于桥接重叠群, 并按照重叠得分由大到小的顺序迭代桥接所有的独立重叠群, 从而形成大型重叠群, 同时通过与非独立重叠群比对消除大型重叠群中的空位, 获得一致性序列。

　　ALPS[33]是一种基于贪心策略的从头拼接算法, 该算法通过整合已测序的肽序列、序列的位置置信度、数据库以及同源性搜索信息, 首次以较高的精确度自动地拼接出完整的单克隆抗体序列。首先, 利用测序产生的肽序列、相近数据库序列和同源性搜索序列建立以 (k-1) -mer为顶点、边长为k的有向DBG。为提高拼接质量, 算法综合序列强度和位置置信度对图中各顶点加权, 从而获得加权DBG。然后, 以图中最大权重顶点为重叠群种子, 向两边选取邻近权重最高的节点进行扩展, 并删除图中已扩展节点, 直到图为空或达到指定重叠群数为止。当未得到完整序列时, 算法需要利用相近数据库序列进行空位填充, 并将重叠群合并为单个完整序列。

　　ISEA[34]是由中南大学的王建新教授团队提出来的一种利用双端信息和拼接距离分布进行从头拼接的迭代种子扩展算法。该算法利用基于DBG的种子扩展策略和打分函数进行处理, 在数学统计层次上保证了序列的拼接精确度并提高了拼接效率, 具有较好的统计学意义。

　　3.2、 基于OLC策略的拼接算法

　　基于该策略的拼接算法主要分为3个阶段。

　　1) Overlap阶段:

　　该阶段对所有参与拼接的reads进行两两比对, 计算其reads间的重叠关系。当两比对reads的重叠区域达到一定阈值时, 将其保留, 用于建立重叠图。

　　2) Layout阶段:

　　根据上一步中的重叠关系建立关于整个reads序列之间的重叠图, 通过遍历重叠图找出能够经过图中大多数节点且只经过一次的路径作为contigs。

　　3) Consensus阶段:

　　通过多序列比对, 使用配对信息将这些contigs拼接组装成一致性序列。但是, 由于目前无法有效降低多序列比对的复杂度, 因此常使用渐进式双序列比对算法替代。基于该策略的拼接算法如图2所示。

　　图2中, 左边区域表示了建立多个reads间的重叠关系, 右边则表示根据已建立的重叠关系而生成的重叠图, 这里设置重叠数量至少为7, 其中浅灰色线则表示两连接对象的重叠碱基数也满足条件。Consensus阶段则表示在获得contigs之后, 将其与原始pair-end数据进行比对, 以确定contigs之间的相对位置并消除空位, 从而将contigs连接成一致性序列。

　　图2 OLC策略拼接示意图

　　Fig.2 Assembly graph based on OLC strategy

　　基于OLC策略的拼接算法[35,36,37]由于涉及到大量的序列比对过程, 用于拼接短reads序列时的计算开销过大, 因此常用于组装一代或三代测序技术产生的较长序列数据。但对于三代测序技术, 其测序reads碱基的错误率达到了15%, 拼接组装该类测序数据时一般都需要对其初始序列进行预纠错。

　　文献[38]提出的HINGE利用拆分重复序列的最优化方案来解决重复序列影响从头拼接长reads的问题。HINGE利用从重叠图中获得的比对信息在reads上加入hinges标记, 这些标记被放置在与无桥接重复序列匹配的reads所对应的开始与结束位置。算法传播该标记信息来处理与拼接无关的重复序列, 并建立一个只能够合并无桥接重复序列片段的最大拆分重复序列重叠图。同时, 该算法利用DALIG-NER[39]能够满足在15%错误率下进行比对的性质, 使得在数据预处理时仅需过滤嵌合体reads, 最后在Consensus阶段中修正拼接错误。

　　文献[40]提出的Canu是一种高效且准确利用自适应k-mers权重以及拆分重复序列来拼接包含大量重复序列以及高错误率reads的PacBio或者Nanopore测序数据的组装算法, 具有低开销、高覆盖度的优势。该算法利用基于tf-idf加权技术的重叠策略来构建关于k-mers的重叠图, 能够最优化处理重复序列对拼接的影响, 并突破计算具有高噪音单分子测序数据重叠关系的瓶颈。另外, 为了最大化Canu算法的准确性以及完整性, Canu在整个拼接过程中多次对reads和重叠区域进行纠错。该算法可运行于独立电脑或者集群服务器上, 并自动选取相对应的算法执行方式。

　　文献[41]提出的DBG2OLC拼接算法是一种综合利用NGS (Next-Generation Sequencing) 和3GS数据来解决高错误率3GS长reads拼接问题并降低测序开销的混合算法。它利用SparseAssembler[42]拼接NGS数据获得带索引的contigs, 并将contigs与3GS数据进行比对, 从而可使用contigs标识符来压缩表示长reads。该操作不仅可以降低算法对测序覆盖度的需求, 而且可以极大地减小建立长reads重叠图以及纠正错误的计算开销。此外, 该算法对长reads利用多序列比对来消除重叠图中的嵌合体reads以及错误contigs标识。

　　文献[43]提出的miniasm算法是一种用于拼接SMRT (Single-Molecule Sequencing in Real Time) 以及ONT (Oxford Nanopore Technologies) 测序所产生的高噪声长reads而无需进行错误纠正和抛光的基于OLC策略的从头拼接算法。该算法能够在实现一定连续性以及精确性的预期下快速且简便地组装序列, 首先通过minimap算法计算所有reads间的重叠信息, 特别地, 该算法中提出的序列比对格式PAF使得它可以与其他比对算法进行融合以支持后续拼接;然后寻求已简化重叠图中满足通过出入度为1的节点的路径作为unitigs。鉴于该算法暂无consensus步骤, Racon[44]算法在其基础上设计了consensus步骤, 通过利用测序长reads与拼接产生的unitigs进行比对, 产生了高质量的一致性序列。

　　文献[45]提出的TULIP拼接算法是一种将大型基因组拼接问题分割为局部从头拼接其长reads子集合的算法。算法在拼接过程中通过比对Illumina测序的短reads序列以及ONT测序的长reads序列来获取它们的比对信息, 并建立以短reads为顶点、比对在同一长reads中连接短reads的序列片段作为边的重叠图, 从而极大地简化了拼接算法的重叠计算过程, 使得计算复杂度接近于线性。此外, 该算法在拼接之前也无需对长reads数据预纠错, 而是利用ONT对最后产生的一致性序列进行抛光处理。

　　文献[46]提出的SSVAGE拼接算法是第一个基于重叠图策略的从头拼接病毒准种的算法。该算法有3种不同的重叠图构建模式:SSVAGE-de-novo表示无参考序列的重叠图构建;SAVAGE-b-ref表示使用其他算法组装样本序列而产生的一致性序列作为参考序列构建重叠图;SAVAGE-h-ref表示输入已存在的高质量参考序列构建重叠图。对于无参考序列的重叠图构建, 算法使用FM-index方法计算reads间的重叠, 反之则通过比对reads与参考序列来建立reads间的重叠关系。该算法通过计算图中的团来识别变异与测序错误, 从而生成了具有高质量的一致性序列。

　　3.3、 基于DBG策略的拼接算法

　　基于DBG策略的拼接算法一般包含如下过程。

　　1) DBG建立阶段:首先将所有待拼接的reads分割成长度为k的序列片段, 称为k-mers, 且同一reads中的相邻k-mers有k-1个碱基重叠;然后利用这些k-mers建立DBG, 其中k-mers作为图的节点, 图中相邻节点间有k-1个碱基重叠, 只有两k-mers首尾的第一个碱基不同。

　　2) contigs构建阶段:在DBG建立完成后, 拼接算法一般需要利用启发式算法消除由测序错误以及杂合位点引起的tips和bubbles等错误来简化图结构, 并找出只经过DBG图中每条边一次的欧拉路径作为contigs。

　　3) scaffolding阶段:将上一步中获得的contigs与原始测序reads进行比对, 并根据比对信息以及reads位置信息填充无连接contigs之间的空位, 通过组装得到最后的一致性序列。

　　基于DBG策略的拼接算法如图3所示。

　　图3 DBG策略拼接示意图

　　Fig.3 Assembly graph based on DBG

　　在DBG图中, k-mers的大小为3 (k值一般为奇数) , 浅灰色图节点表示tips结构, 深灰色图节点则为重复序列, 其中上下两回路所连接的图节点都表示bubbles结构。简化该气泡结构后可得碱基序列, 如图3中的序列TCCGTA和TCTCCA。右下角为contigs拼接结果, 其中Consensus阶段和OLC策略类似。

　　基于DBG策略的拼接算法[47,48,49]被广泛应用于拼接来自SOLiD和Solexa平台测序产生的短reads序列。DBG结构最早是介绍并运用在EULER[38]拼接算法中, 该数据结构非常适合于对具有重叠关系的短重复reads序列进行测序, 且能够极大地减少序列冗余所带来的内存消耗等问题。DBG算法很好地弥补了HTS数据中测序序列长度较短的缺点, 在拼接过程中支持并行化且只需要较少的比对操作, 极大地缩短了基因组序列的拼接时间, 提高了拼接效率。但由于错误的k-mers和大量重复序列会极大地降低基于该种策略算法的组装效果, 因此该类算法一般都需要对拼接reads和DBG图或已拼接完成的一致性序列进行纠错, 以提高拼接精确度, 同时需利用三代测序数据、“linked reads”数据以及光学图谱技术提高拼接的完整度。现有拼接算法大部分都以该策略作为主要的算法数据结构。

　　3.3.1、 ALLPATHS

　　ALLPATHS[50]是一种被用于拼接大型基因组序列的基于DBG策略的算法, 它由Broad Institute of MIT and Harvard研究中心于2009年研发出来, 主要是为了解决难以利用具有高重复率特征的二代测序短reads进行从头拼接的问题。该算法不仅可以处理短reads基因组数据, 而且可以应用于所有的DNA序列数据, 同时具有较高的拼接完整性、连续性以及正确性, 并保留了由序列多样性所引起的内在歧义。

　　该算法主要有两个关键过程。首先, 对于一个配对read, 找出通过该read的所有序列路径;其次, 使用配对信息对基因组进行分离, 同时选取满足一定长度和复本数量的路径合并成无分支结构的unipaths, 从而建立unipaths图, 使局部拼接可并行化。在执行过程中, 超短reads (一般长度为25～50 bp) 之间具有大量的overlaps信息, 但这些overlaps信息大部分是错误的 (不是连续的短reads) 。为了解决这一问题, ALLPATHS算法引入了k-mers编号算法, 使得k-mers可以按照reads的顺序进行连续编号, 进而可以根据编号的差别来避免不必要的overlaps计算开销, 同时提高序列拼接的连续性。为了达到更高的拼接准确性和完整性, ALLPATHS在拼接过程中对所有的reads进行错误纠正[51], 同时利用所有局部拼接产生的结果之间的重叠信息组合生成一个全局拼接图, 最后利用pair-end信息消除该全局图中的错误分支结构。

　　2011年, Broad Institute of MIT and Harvard研发中心基于并行测序技术产生的大规模哺乳动物基因组序列的拼接组装问题提出了ALLPATHS-LG[52]拼接算法。该算法是测序技术与高性能计算方法的结合体, 对ALLPATHS中算法在处理重复序列、错误纠正等方面进行改进, 并使用了跳查文库。该算法虽然要求必须至少制备一个具有overlapping的paired-reads文库, 但是在序列组装错误率与拼接序列连续性方面却取得了平衡, 具有较好的基因组覆盖度和精确度, 是一种公认的较好基因组从头拼接组装软件。

　　3.3.2、 SOAPdenovo

　　SOAPdenovo[53]基因组序列拼接软件是华大基因在2010年研究设计的一种解决难以从头拼接由NGS并行DNA测序技术产生的大规模重复短序列的拼接器, 在处理序列中产生的SV (Structure Variation) 问题和indels问题 (插入和缺失等) 方面具有较大的优势, 能够更好地促进在核苷酸层次上准确理解生物进化历史和生物学过程, 是一种用于构造大型参考基因组的有效从头拼接组装算法, 可以进行较高精确度的探索, 并分析未知个体生物基因。

　　该算法首先对所有的k-mers建立哈希索引, 并行化处理已分割的reads数据集, 同时利用动态规划算法和等位基因的方式来消除或修正低频率的k-mers。其将从已修正的DBG中获得的欧拉路径作为contigs, 并将获得的contigs重新与所有的reads进行比对来确定contigs间的相对顺序, 以正确连接contigs。在scaffolding阶段, 算法通过迭代合并重叠的contigs以及pair-end信息消除由重复序列导致的contigs间空位, 使得待组装序列更为完整。

　　SOAPdenovo的扩展版本SOAPdenovo2[54]和SOAPdenovo-Tran[55]在DBG构建阶段利用一种多k-mers值策略, 通过由小到大迭代地利用k值来消除不同长度的重复序列, 充分利用了小k-mers处理低覆盖度与错误reads的优势以及大k-mers处理重复序列的高效性特征;在scaffolds构建阶段也使用迭代的拼接距离来消除空位和杂合contigs, 进一步提高了拼接组装的效率、敏感性以及准确率。文献[55]可被用于拼接转录组。

　　3.3.3、 IDBA-UD

　　IDBA-UD[56]是由香港大学的彭煜等提出的一种解决单细胞测序与宏基因组测序技术难以对不同物种间或同物种中基因组的不同区域的不均匀测序深度进行测序的从头拼接算法。相较于其他已存在的组装算法, 该算法能够在不均匀测序深度数据条件下构造出较长且高拼接精确度的contigs。

　　该算法首先对待测序的reads使用合适的k值进行质控, 然后对于建立的DBG, 根据序列中测序深度的高低两种情况, 利用与测序深度相关的阈值来消除图结构中的错误k-mers, 并且使用双端测序信息来解决图中的重复分支问题, 获得了完整且准确的contigs。算法的主要执行过程为:首先, 针对序列的不同测序深度建立相应的k值, 并根据k值从小到大迭代地建立DBG;然后, 求各图中的欧拉路径并将其作为contigs, 对获得的contigs和失配的k-mers使用双端信息消除错误分支, 提高局部拼接的精确度并填补空位。在每一个过程中, 都需要将获得的contigs与包含待测序reads数最多的置信contigs进行比对来纠正错误, 每个迭代的DBG建立都需不断进行错误修正来保证局部拼接过程的正确性, 从而提高拼接的精确度。

　　在进行单细胞序列数据或宏基因组序列数据拼接时, 由于测序深度不均匀的影响, 常见的处理DBG图中出现错误k-mers、空位问题以及错误分支结构的方法难以提高序列拼接性能。因此, IDBA-UD改进了velvet-SC[57]中利用一个固定的阈值来解决在不同测序深度下的单细胞序列数据的算法, 根据测序深度的不同对相关阈值作适应性处理, 从而更能符合单细胞与宏基因组中测序深度不均匀的特性。IDBA-UD算法中对不同测序深度设置不同阈值的方法已经被成功应用于转录基因组组装算法[54,58]。

　　3.3.4、 metaSPAdes

　　metaSPAdes[59]是一种通过融合已经被证明了的一系列SPAdes[60,61,62,63,64]工具中的方法来拼接单细胞和高度多态的二倍体基因组的拼接器, 其能够并行化处理宏基因组拼接过程中的各项挑战, 如菌株之间差异细微、不同物种的冗余度水平各异、菌株共享高保守区域以及大量冗余度不同的相近菌株混合等。算法基于交叉合成的数据集和与被拼接宏基因组相关的真实数据集, 解决了在宏基因组基准测试中无参考基因组的问题。测试结果显示, 该算法在scaffold长度、基因预测能力以及read与scaffold比对统计等方面具有较大优势。

　　算法首先利用SPAdes[60]对文库中所有的reads建立DBG, 然后通过简化该图将其转化为拼接图, 并将拼接图中获得的一致性路径作为该宏基因组中的长基因组片段。该算法适用于对具有多种不同的测序深度混合菌株进行拼接, 并在拼接精确度以及连续性方面取得了平衡。在简化DBG操作中, 算法删除了图中的tips, 但在去除bulge (类似bubbles结构) 结构的过程中保留了其原始信息, 该信息可用于识别scaffolding中的重复序列, 提高了拼接混合菌株的一致性序列质量。与传统拼接算法使用全局覆盖度阈值来删除图中低覆盖度的边不同, metaSPAdes首先计算点与边的覆盖度值, 若边覆盖度乘以阈值比例小于所连接点的覆盖度, 则断开该连接, 而非直接删除该边, 这样可以尽可能保留稀有菌株的信息。在scaffolding阶段时, 算法在ExSPAnder[61]算法的重复序列确定规则中考虑了局部覆盖度因素, 消除了重复路径的影响, 并利用局部覆盖度与分支间边的覆盖度的关系处理了图中的分支问题。

　　该算法支持简化DBG阶段的并行化, 同时对k-mers使用了hash存储和扩展矩阵, 从而快速地提高了简化DBG阶段以及scaffold阶段的存储效率, 使得算法能够拼接大规模的复杂宏基因组数据集。

　　结束语 高通量测序技术是基因组序列拼接算法发展的重要催化剂之一。处理快速增长的海量基因组序列数据, 对基因疾病进行预测与治疗, 以及对生物同源性分析等问题的研究, 成为了序列拼接组装算法发展的关键目标和主要研究动力, 但也给未来的基因组拼接组装算法的研究与发展带来了巨大的挑战。相比于第一代测序技术, 研究人员能够利用高通量测序技术获得较高的序列测序深度, 但测序reads长度变短、reads错误率增高以及重复序列对拼接的影响越来越大, 且研究方向由传统的单个物种的全基因组序列组装转变为目前多物种混杂的短reads数据集组装与分析, 同时计算方式也由本地计算逐渐发展为以“云计算”为基础的互联网云计算。因此, 研究人员需开发出新型的拼接组装算法来应对高通量测序下大量短reads数据迅速增长的需求, 并结合三代测序技术的优势, 解决在序列拼接组装过程中出现的拼接组装精确度低、内存利用率不高和基因序列拼接不完整等问题。根据对以上算法项目的分析与对比, 将来的研究可从以下几个方面做出努力。

　　1) 构建实用的支持高效序列拼接算法开发的系统。该系统应具有较为简单的使用界面以及配置环境, 能够集成在现有运算条件下解决生物信息拼接问题域的大规模算法库以增强算法的交互性, 并具有较广泛的应用前景和较高的应用价值。

　　2) 探究具有综合装配组装能力的组装算法。产生式编程是一种为了发现超出对象、概念与特征范畴之外的编程和设计表达形式。因此, 研究一种面向动态装配的产生式算法, 能够极大地整合对现有分布式下的基因组序列数据集的计算方式;对其进行分配与管理, 以无障碍地组合现有算法, 甚至产生新式的基因组拼接算法。

　　3) 开发联合机器学习与统计计算的基因组拼接算法。目前算法主要还是以基于统计计算为主, 尚需人为地进行序列参数调整与实现, 同时只适用于解决人类已知的相关生物信息拼接问题域。因此, 将机器学习的智能化优势运用于统计计算算法中, 实现两者的有机结合, 是一条有希望的途径。

　　参考文献

　　[1] WARD R M, SCHMIEDER R, HIGHNAM G, et al.Big data challenges and opportunities in high-throughput sequencing[J].Systems Biomedicine, 2013, 1 (1) :29-34.
　　[2] PEARSON W R Y, LIPMAN D J.Improved tools for biological sequence analysis[J].Proceedings of the National Academy of Sciences of the United Sates of America, 1988, 85 (46) :16138-16143.
　　[3] ALTSCHUL S F, MADDEN T L, SCH?FFER A A, et al.Gapped BLAST and PSI-BLAST:a new generation of protein database search programs[J].Nucleic Acids Research, 1997, 25 (17) :3389-3402.
　　[4] LARKIN M A, BLACKSHIELDS G, BROWN N P, et al.Clus- tal W and Clustal X version 2.0[J].Bioinformatics, 2007, 23 (21) :2947-2948.
　　[5] DARLING A E, MAU B, PERNA N T.progressive Mauve:Mul- tiple Genome Alignment with Gene Gain, Loss and Rearrangement[J].PLOS One, 2010, 5 (6) :e11147.
　　[6] BLANCHETTE M, KENT W J, RIEMER C, et al.Aligning multiple genomic sequences with the threaded blockset aligner[J].Genome Research, 2004, 14 (4) :708-715.
　　[7] CANTOR C R.Orchestrating the Human Genome Project[J].Science, 1990, 248 (4951) :49-51.
　　[8] CONSORTIUM T G P.A global reference for human genetic variation, the 1000 Genomes Project Consortium[J].Nature, 2015, 526:68-74.
　　[9] CONSORTIUM T U.The UK10K project identifies rare va- riants in health and disease[J].Nature, 2015, 526 (7571) :82-90.
　　[10] WATSON M.Illuminating the future of DNA sequencing[J].Genome Biology, 2014, 15 (2) :108.
　　[11] Sanger F, Nicklen S, Coulson A R.DNA sequencing with chain-terminating inhibitors[J].Proceedings of the National Academy of Sciences of the United States of America, 1977, 74 (12) :5463-5467.
　　[12] MOROZOVA O.Applications of next-generation sequencing technologies in functional genomics[J].Genomics, 2008, 92 (5) :255-264.
　　[13] WOOLEY J C, GODZIK A, FRIEDBERG I.A Primer on Meta- genomics[J].PLOS Computational Biology, 2010, 6 (2) :e1000667.
　　[14] WU X, ZHU X, WU G Q, et al.Data Mining with Big Data[J].IEEE Transactions on Knowledge & Data Engineering, 2014, 26 (1) :97-107.
　　[15] FONSECA N A, RUNG J, BRAZMA A, et al.Tools for mapping high-throughput sequencing data[J].Bioinformatics, 2012, 28 (24) :3169-3177.
　　[16] NIEDRINGHAUS T P, MILANOVA D, KERBY M B, et al.Landscape of Next-Generation Sequencing Technologies[J].Analytical Chemistry, 2011, 83 (12) :4327-4341.
　　[17] HARRIS T D, BUZBY P R, BABCOCK H, et al.Single-molecule DNA sequencing of a viral genome[J].Science, 2008, 320 (5872) :106-109.
　　[18] FLUSBERG B A, WEBSTER D, LEE J, et al.Direct detection of DNA methylation during single-molecule, real-time sequencing[J].Nature Methods, 2010, 7 (6) :461-465.
　　[19] RUSK N.Cheap third-generation sequencing[J].Nature Me- thods, 2009, 6 (4) :244-244.
　　[20] CHIN C S, PELUSO P, SEDLAZECK F J, et al.Phased Diploid Genome Assembly with Single Molecule Real-Time Sequencing[J].Nature Methods, 2016, 13 (12) :1050-1054.
　　[21] HEEREMA S J, DEKKER C.Graphene nanodevices for DNA sequencing[J].Nature Nanotechnology, 2016, 11 (2) :127-136.
　　[22] HEATHER J M, CHAIN B.The sequence of sequencers:The history of sequencing DNA[J].Genomics, 2016, 107 (1) :1-8.
　　[23] SHENDURE J, JI H.Next-generation DNA sequencing[J].Nature Biotechnology, 2008, 26 (10) :1135-1145.
　　[24] JACKMAN S D, VANDERVALK B P, MOHAMADI H, et al.ABySS 2.0:resource-efficient assembly of large genomes using a Bloom filter[J].Genome Research, 2017, 27 (5) :768-777.
　　[25] ZIMIN A V, STEVENS K A, CREPEAU M W, et al.An improved assembly of the loblolly pine mega-genome using long-read single-molecule sequencing[J].GIGA Science, 2017, 6 (1) :1-4.
　　[26] MOSTOVOY Y, LEVYSAKIN M, LAM J, et al.A hybrid approach for de novo human genome sequence assembly and phasing[J].Nature Methods, 2016, 13 (7) :587-590.
　　[27] LIU Y, BERTIL S, MASKELL D L.Parallelized short read assembly of large genomes using de Bruijn graphs[J].BMC Bioinformatics, 2011, 12 (1) :354.
　　[28] WARREN R L, SUTTON G G, JONES S J M, et al.Assembling millions of short DNA sequences using SSAKE[J].Bioinforma-tics, 2007, 23 (4) :500-501.
　　[29] JECK W R, REINHARDT J A, BALTRUS D A, et al.Extending assembly of short DNA sequences to handle error[J].Bioinformatics, 2007, 23 (21) :2942-2944.
　　[30] DOHM J C, LOTTAZ C, BORODINA T, et al.SHARCGS, a fast and highly accurate short-read assembly algorithm for de novo genomic sequencing[J].Genome Research, 2007, 17 (11) :1697-1706.
　　[31] FARRANT G K, HOEBEKE M, PARTENSKY F, et al.WiseScaffolder:an algorithm for the semi-automatic scaffolding of Next Generation Sequencing data[J].BMC Bioinformatics, 2015, 16 (1) :281.
　　[32] CAO M D, NGUYEN S H, GANESAMOORTHY D, et al.Scaffolding and completing genome assemblies in real-time with na-nopore sequencing[J].Nature Communications, 2017, 8:14515.
　　[33] HIEU T N, ZIAUR R M, HE L, et al.Complete De NovoAssembly of Monoclonal Antibody Sequences[J].Scientific Reports, 2016, 6:31730.
　　[34] MIN L, LIAO Z, HE Y, et al.ISEA:Iterative Seed-Extension Algorithm for De Novo Assembly Using Paired-End Information and Insert Size Distribution[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, 14 (4) :916-925.
　　[35] MYERS E W, SUTTON G G, DELCHER A L, et al.A Whole-Genome Assembly of Drosophila[J].Science, 2000, 287 (5461) :2196-2204.
　　[36] DE L B M, MCCOMBIE W R.Assembling genomic DNA se- quences with PHRAP[J].Current Protocols in Bioinformatics, 2007, 17 (1) :11.4.1-11.4.15.
　　[37] MARGULIES M, EGHOLM M, ALTMAN W E, et al.Genome sequencing in microfabricated high-density picolitre reactors[J].Nature, 2005, 437 (7057) :376-380.
　　[38] KAMATH G M, SHOMORONY I, XIA F, et al.HINGE:long-read assembly achieves optimal repeat resolution[J].Genome Research, 2017, 27 (5) :747-756.
　　[39] MYERS G.Efficient Local Alignment Discovery amongst Noisy Long Reads[M]//Algorithms in Bioinformatics.Berlin:Sprin-ger, 2014:52-67.
　　[40] KOREN S, WALENZ B P, BERLIN K, et al.Canu:scalable and accurate long-read assembly via adaptive k-mer weighting and repeat separation[J].Genome Research, 2017, 27 (5) :722-736.
　　[41] YE C, HILL C M, WU S, et al.DBG2OLC:Efficient Assembly of Large Genomes Using Long Erroneous Reads of the Third Generation Sequencing Technologies[J].Scientific Reports, 2016, 6 (X) :31900.
　　[42] YE C, MA Z S, CANNON C H, et al.Exploiting sparseness in de novo genome assembly[J].BMC Bioinformatics, 2012, 13 (S6) :S1.
　　[43] LI H.Minimap and miniasm:fast mapping and de novo assembly for noisy long sequences[J].Bioinformatics, 2015, 32 (14) :2103-2110.
　　[44] VASER R, SOVI, et al.Fast and accurate de novo genome assembly from long uncorrected reads[J].Genome Research, 2017, 27 (5) :737-746.
　　[45] JANSEN H J, LIEM M, JONGRAADSEN S A, et al.Rapid de novo assembly of the European eel genome from nanopore sequencing reads[J].Scientific Reports, 2017, 7 (1) :7213.
　　[46] BAAIJENS J A, AZE A, RIVALS E, et al.De novo assembly of viral quasispecies using overlap graphs[J].Genome Research, 2017, 27 (5) :835-848.
　　[47] PENG G, JI P, ZHAO F.A novel codon-based de Bruijn graph algorithm for gene construction from unassembled transcriptomes[J].Genome Biology, 2016, 17 (1) :232.
　　[48] CAMERON D L, SCHROEDER J, PENINGTON J S, et al.GRIDSS:sensitive and specific genomic rearrangement detection using positional de Bruijn graph assembly[J].Genome Research, 2017, 27 (12) :1-11.
　　[49] WEISENFELD N I, KUMAR V, SHAH P, et al.Direct determination of diploid genome sequences[J].Genome Research, 2017, 27 (5) :757-767.
　　[50] BUTLER J, MACCALLUM I, KLEBER M, et al.ALLPATHS:de novo assembly of whole-genome shotgun microreads[J].Genome Research, 2008, 18 (5) :810-820.
　　[51] PEVZNER P A, TANG H, WATERMAN M S.An Eulerian path approach to DNA fragment assembly[J].Proceedings of the National Academy of Sciences of the United Sates of America, 2001, 98 (17) :9748-9753.
　　[52] GNERRE S, JAFFE D B.High-quality draft assemblies of mammalian genomes from massively parallel sequence data[J].Proceedings of the National Academy of Sciences of the United Sates of America, 2011, 108 (4) :1513-1518.
　　[53] LI R, ZHU H, RUAN J, et al.De novo assembly of human genomes with massively parallel short read sequencing[J].Genome Research, 2010, 20 (2) :265-272.
　　[54] LUO R, LIU B, XIE Y, et al.SOAPdenovo2:an empirically improved memory-efficient short-read de novo assembler[J].GIGA Science, 2012, 1 (1) :18.
　　[55] XIE Y, WU G, TANG J, et al.SOAPdenovo-Trans:de novo transcriptome assembly with short RNA-Seq reads[J].Bioinformatics, 2014, 30 (12) :1660-1666.
　　[56] PENG Y, LEUNG H C M, YIU S M, et al.IDBA-UD:a de novo assembler for single-cell and metagenomic sequencing data with highly uneven depth[J].Bioinformatics, 2012, 28 (11) :1420-1428.
　　[57] CHITSAZ H, YEE-GREENBAUM J L, TESLER G, et al.Efficient de novo assembly of single-cell bacterial genomes from short-read data sets[J].Nature Biotechnology, 2011, 29 (10) :915-921.
　　[58] PENG Y, LEUNG H C M, YIU S M, et al.IDBA-tran:a more robust de novo de Bruijn graph assembler for transcriptomes with uneven expression levels[J].Bioinformatics, 2013, 29 (13) :326-334.
　　[59] NURK S, MELESHKO D, KOROBEYNIKOV A, et al.metaSPAdes:a new versatile metagenomics assembler[J].Genome Research, 2017, 27 (5) :824-834
　　[60] BANKEVICH A, NURK S, ANTIPOV D, et al.SPAdes:A New Genome Assembly Algorithm and Its Applications to Single-Cell Sequencing[J].Journal of Computational Biology, 2012, 19 (5) :455-477.
　　[61] PRJIBELSKI A D, VASILINETC I, BANKEVICH A, et al.ExSPAnder:a universal repeat resolver for DNA fragment assembly[J].Bioinformatics, 2014, 30 (12) :293-301.
　　[62] SAFONOVA Y, BANKEVICH A, PEVZNER P A.dipSPAdes:Assembler for Highly Polymorphic Diploid Genomes[C]//International Conference on Research in Computational Molecular Biology.New York:Springer-Verlag, 2014:265-279.
　　[63] ANTIPOV D, KOROBEYNIKOV A, MCLEAN J S, et al.hybridSPAdes:an algorithm for hybrid assembly of short and long reads[J].Bioinformatics, 2015, 32 (7) :1009-1015.
　　[64] VASILINETC I, PRJIBELSKI A D, GUREVICH A, et al.Assembling short reads from jumping libraries with large insert sizes[J].Bioinformatics, 2015, 31 (20) :3262-3268.

周卫星,石海鹤.高通量测序中序列拼接算法的研究进展[J].计算机科学,2019,46(05):36-43.