剑指 Offer II 010. 和为 k 的子数组

给定一个整数数组和一个整数 k ，请找到该数组中和为 k 的连续子数组的个数。

示例 1：

输入:nums = [1,1,1], k = 2
输出: 2
解释: 此题 [1,1] 与 [1,1] 为两种不同的情况

示例 2：

输入:nums = [1,2,3], k = 3
输出: 2

提示:

1 <= nums.length <= 2 * 104
-1000 <= nums[i] <= 1000
-107 <= k <= 107

这个题目做出来不难，直接暴力枚举。但是利用哈希表和前缀和优化的过程我一直不是很理解，所以写下这篇文章来一点一点的研究，希望能对大家有所帮助

首先，先看最简单的暴力解法：

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.length; ++start) {
            int sum = 0;
            for (int end = start; end < nums.length; ++end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

这个解法相比大家都能想的出来，就不在此深究了。
接下来看另外一种暴力解法：

利用前缀和暴力解题：

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        int len = nums.length;
        int[] pre = new int[len+1];

        for(int i=1;i<=len;i++){
            pre[i] = pre[i-1]+nums[i-1];
        }

        for(int i=0;i<=len;i++){
            for(int j=i+1;j<=len;j++){
                if(pre[j] - pre[i] == k) ++count;
            }
        }
        return count;
    }
}

下面讲一下思路：

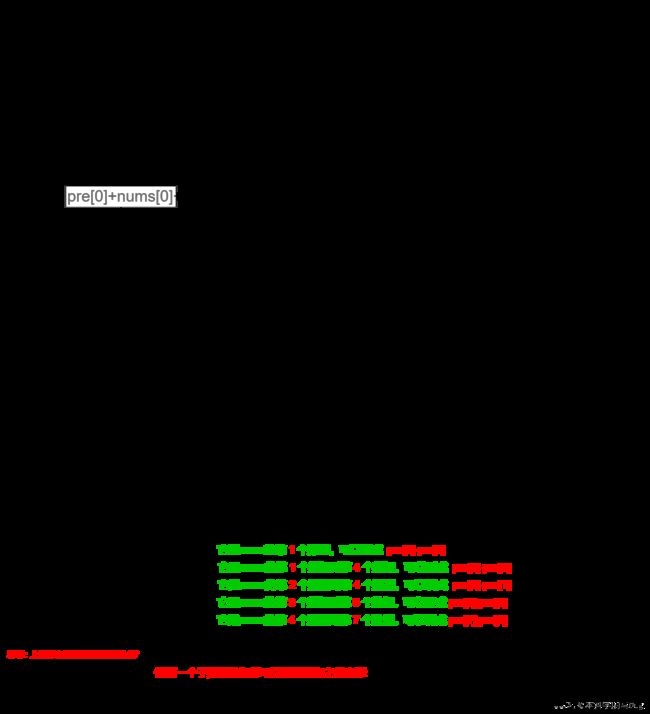
这种做法依旧很好理解。时间复杂度依旧很高，我们要继续优化。
这种双循环会使得有个别元素遍历了很多次。这是可以优化的地方。
下面我们研究一下 pre[i] , pre[j] ,和 k 的关系

看到这里大家应该已经理解了，当然也可能是我描述的不够清晰导致大家没能理解（见谅）
代码如下：

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        int len = nums.length;
        int[] pre = new int[len+1];
        Map<Integer,Integer> map = new HashMap();
        map.put(0,1);
        for(int i=1;i<=len;i++){
            pre[i] = pre[i-1]+nums[i-1];
        }

        for(int i=1;i<=len;i++){
            if(map.containsKey(pre[i]-k)){
                count+=map.get(pre[i]-k);
            }
            map.put(pre[i], map.getOrDefault(pre[i], 0) + 1);
        }
        return count;
    }
}

这样只用一个循环就搞定了。但是还可以再优化
我们思考 pre[] 数组真的需要吗？

for(int i=1;i<=len;i++){
        if(map.containsKey(pre[i]-k)){
            count+=map.get(pre[i]-k);
        }
        map.put(pre[i], map.getOrDefault(pre[i], 0) + 1);
}

我们发现 每次循环只用了 当前的 pre[i]；前面的都没用到

for(int i=1;i<=len;i++){
            pre[i] = pre[i-1]+nums[i-1];
}

for(int i=1;i<=len;i++){
        if(map.containsKey(pre[i]-k)){
            count+=map.get(pre[i]-k);
        }
        map.put(pre[i], map.getOrDefault(pre[i], 0) + 1);
}

那么上面这个循环完全可以写进下面这个循环

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        int len = nums.length;
        int pre = 0;//用变量去迭代前缀和就行
        Map<Integer,Integer> map = new HashMap();
        map.put(0,1);
        
        for(int i=0;i<len;i++){//这里 i 要从 0 开始，因为操作的是 nums[i] 
            pre+=nums[i];//这一步就相当于 pre[i] ,大家可以理解一下
            if(map.containsKey(pre-k)){
                count+=map.get(pre-k);
            }
            map.put(pre, map.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

那么，这篇文章就到此为止啦，希望能帮助到大家
博主才疏学浅，如有错误，请指正