C++实现图 - 05 拓扑排序

数据结构与算法专栏 —— C++实现

写在前面：
今天来讲另一个非常重要的知识点 —— 拓扑排序。咋一看好像是一个排序算法，然而它和排序扯不上半点关系，它可以用于判断我们的图中是否存在有向环。

什么是有向无环图？

听名字应该很好理解，就是图中存在有向环，我们先看一个有向无环图。

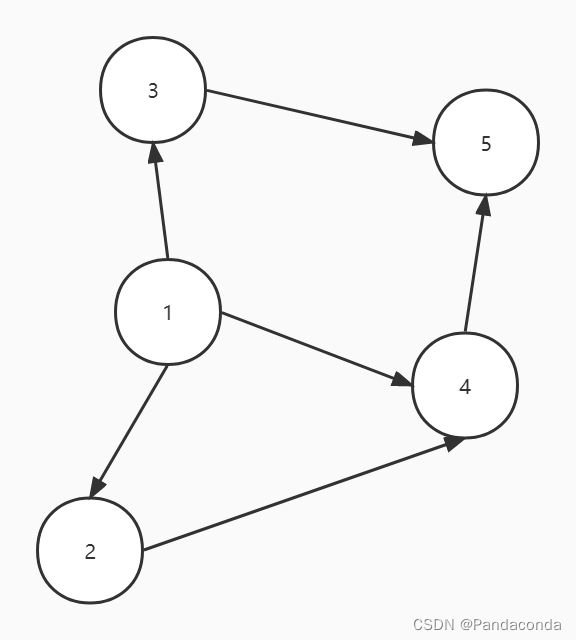
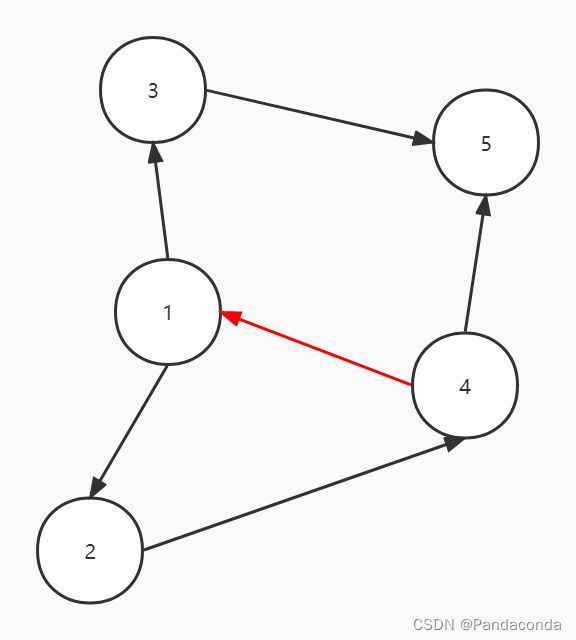
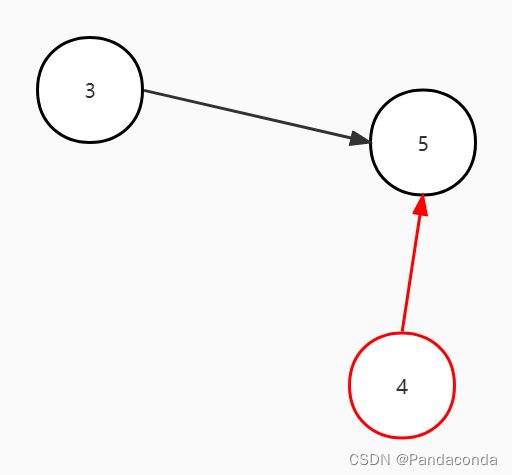
我们只需要改动上图一条边，它就成为了一个有环图。

拓扑排序

算法思想

拓扑排序就是对一个有向无环图构造拓扑序列的过程，听起来可能不知道从何下手，其实算法步骤很简单：

1. 在有向图中选一个没有前驱的顶点并输出。
2. 从图中删除该顶点和所有以它为尾的弧。

重复上述两步，直至全部顶点均已输出，或者当前图不存在无前驱的顶点为止，后一种情况说明有向图中存在环。

下面我们将用有向无环图和有向有环图进行举例。

有向无环图

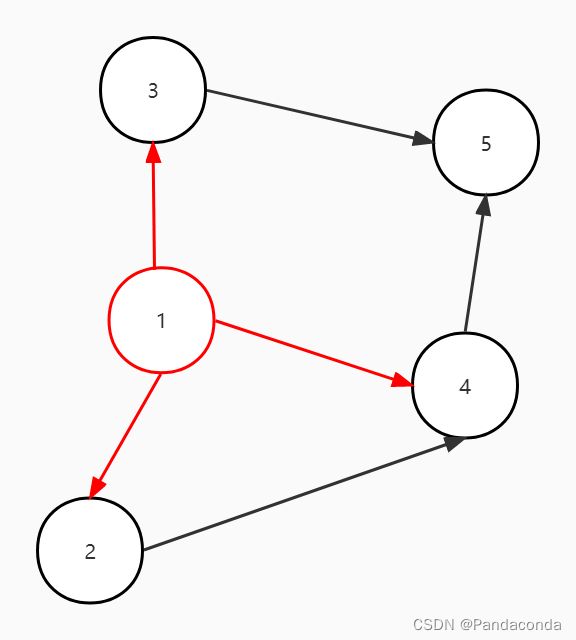
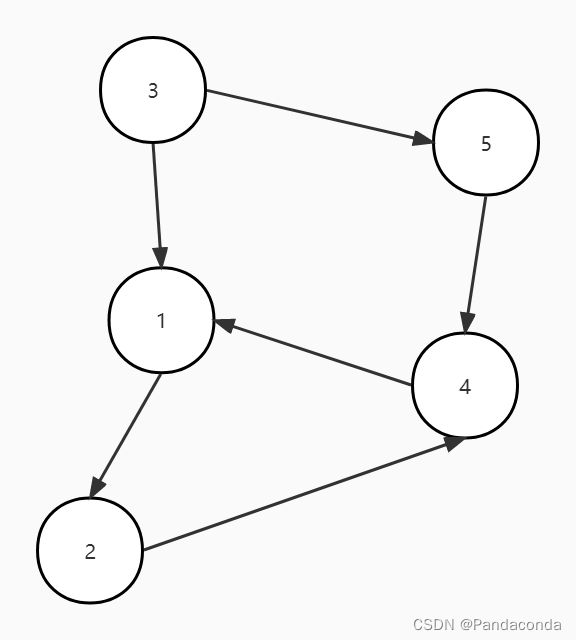
下图是一张有向无环图，现在我们开始进行算法步骤：

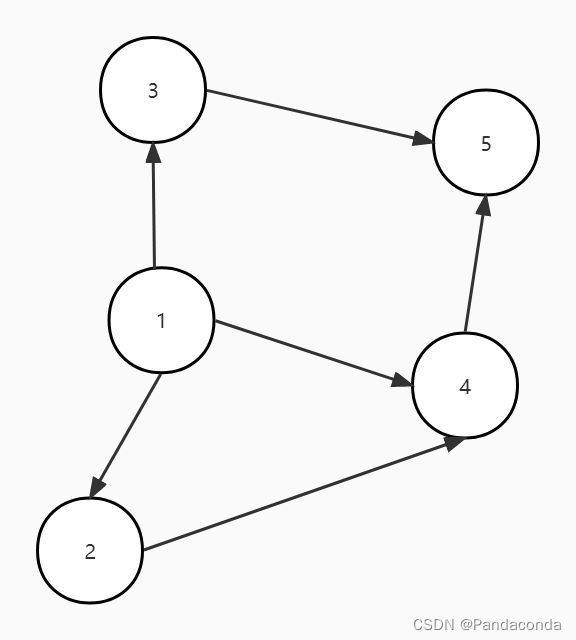
第一步：找到图中没有前驱的结点，目前图中只有一个结点 1 没有前驱。

第二步：输出并删除结点 1 以及所有以它为尾的弧。

第三步：找到没有前驱的结点 2 和结点 3 ，假设先输出结点 2 。

第四步：输出并删除结点 2 以及所有以它为尾的弧。

第五步：找到没有前驱的结点 3 和结点 4 ，假设先输出结点 4 。

第六步：输出并删除结点 4 以及以它为尾的弧。

第七步：找到没有前驱的结点 3 并输出。

第八步：输出并删除结点 3 以及以它为尾的弧。

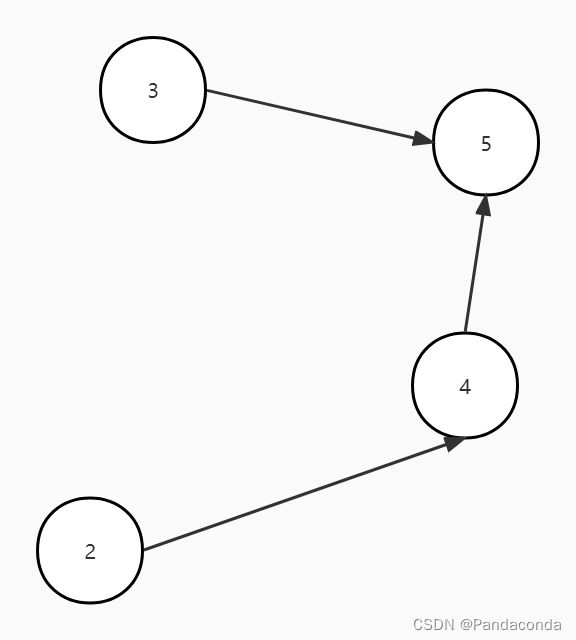
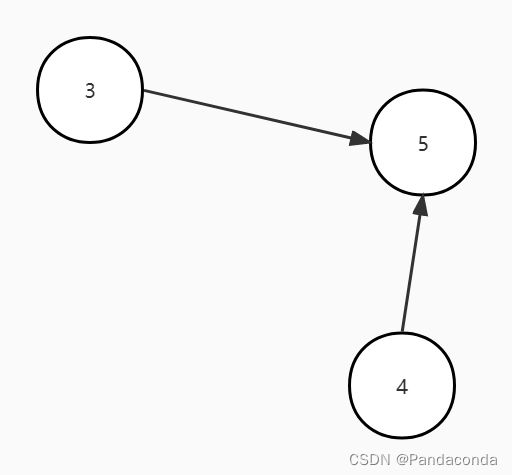
至此，只剩结点 5 ，故该图是一个有向无环图。

有向有环图

其实操作和上面类似，我们直接上图：

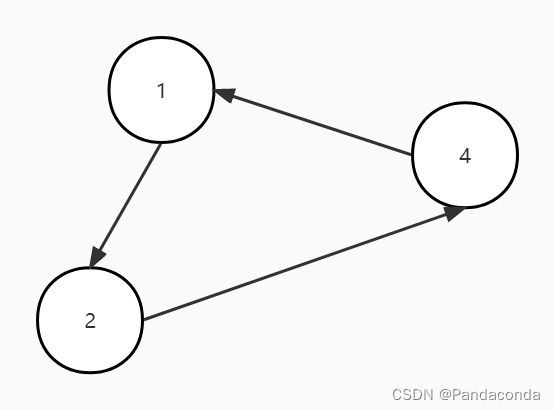
初始图如上，结点 2、3、4 构成了一个环，按照上面的操作进行，我们依次删除没有前驱的结点，最终会得到下面这张图：

可以发现，算法结束后仍然存在三个结点，故该图是一个有环图。

算法实现

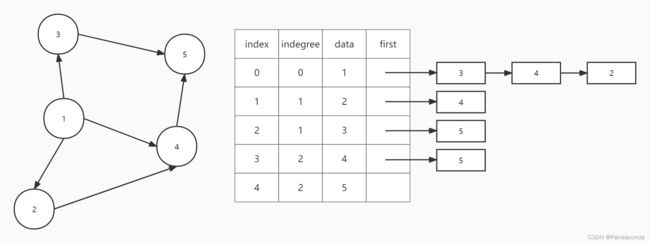
为了实现这个算法，这里我们需要用到邻接表，并且我们还额外需要一个数组存储每个结点入度（指向该结点的结点数量），如果为 0 则说明该结点没有前驱结点即没有结点指向它。

所以现在就很清楚了，我们首先要做的就是去寻找数组中入度为 0 的点，然后将它们全部放入一个栈中，再依次弹出来进行后续操作，直接上图（这里就拿有向无环图来举例啦）：

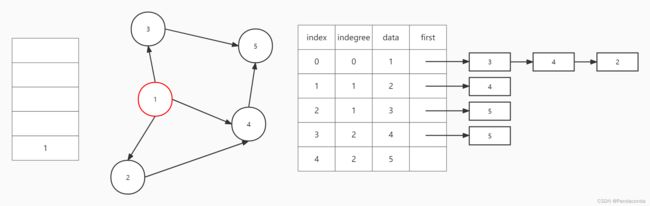
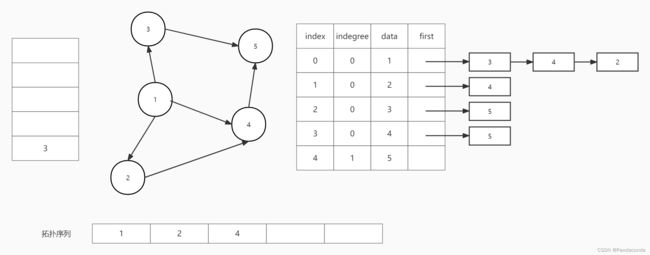
第一步：遍历所有结点，将入度为 0 的点入栈即将结点 1 入栈。

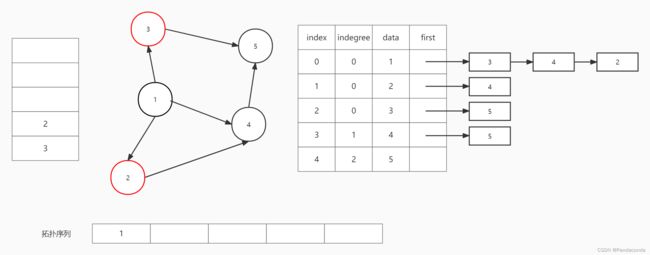
第二步：弹出栈顶元素即结点 1 并输出，然后遍历结点 1 的邻接结点，将它们的入度减 1 。先将结点 3 的入度减 1 ，发现为 0 则入栈；再将结点 4 的入度减 1 ，发现不为 0 则不如栈；最后将结点 2 的入度减 1 ，发现为 0 则入栈。

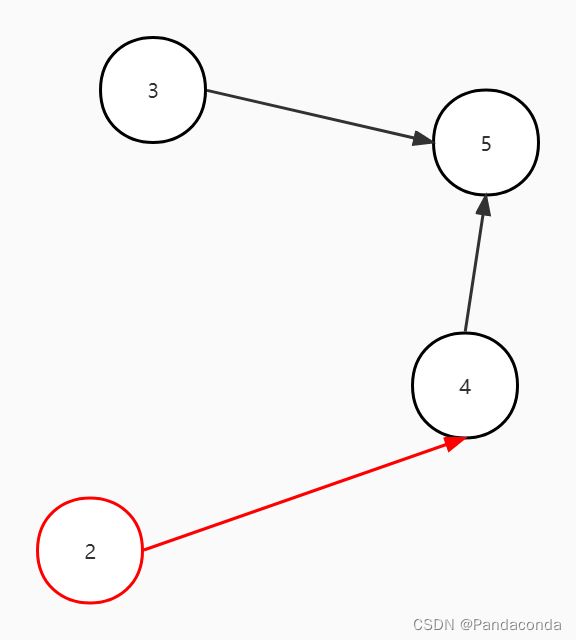
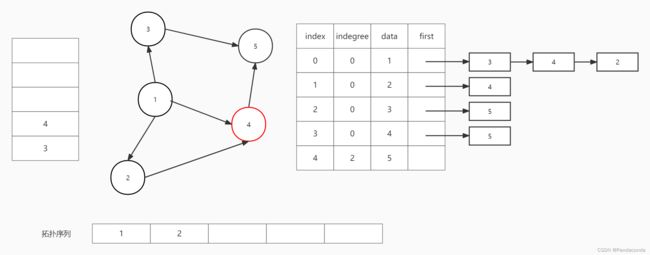
第三步：弹出栈顶元素即结点 2 并输出，然后遍历结点 2 的邻接结点，将它们的入度减 1 。将结点 4 的入度减 1 ，发现为 0 则入栈。

第四步：弹出栈顶元素即结点 4 并输出，然后遍历结点 4 的邻接结点，将它们的入度减 1 。将结点 5 的入度减 1 ，发现不为 0 则不入栈。

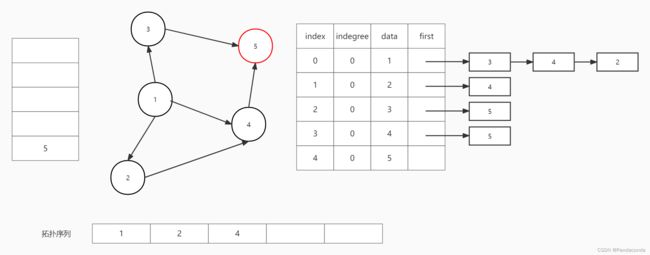
第五步：弹出栈顶元素即结点 3 并输出，然后遍历结点 3 的邻接结点，将它们的入度减 1 。将结点 5 的入度减 1 ，发现为 0 则入栈。

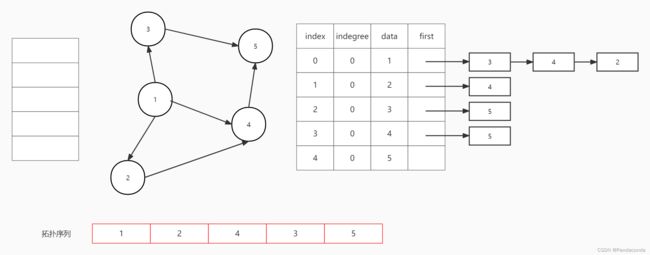
第六步：弹出栈顶元素即结点 5 并输出，结点 5 没有后继结点。

第七步：栈中元素为空，算法结束。此时数组中所有结点入度都为 0 ，故该图是有向无环图。

全部代码

这里的栈操作我们通过手写实现，如果对该操作不太熟悉的小伙伴可以回溯到我们之前的栈那一讲看看~

线性表 - 04 栈

#include 
using namespace std;
#define MAXVERTIES 20
#define OK 1
#define ERROR 0

int indegree[MAXVERTIES] = { 0 };	//用于存储入度信息

/*
5
1 2 3 4 5
6
1 2
1 4
1 3
2 4
3 5
4 5
*/

//定义结点
struct VexNode {
	int data;
	VexNode *next;
};

//定义弧
struct ArcNode {
	int data;
	VexNode *firstacr = NULL;
};

//定义邻接表
struct GraphList {
	ArcNode arclist[MAXVERTIES];
	int vexnum, arcnum;
};

//定义栈
struct Stack {
	int Sacklist[MAXVERTIES] = { 0 };
	int top = -1;
};

//入栈操作
void Push(Stack &S, int key) {
	if (S.top == MAXVERTIES) {
		cout << "栈已满！" << endl;
		return;
	}
	S.top++;
	S.Sacklist[S.top] = key;
}

//出栈操作
int Pop(Stack &S) {
	if (S.top == -1) {
		cout << "栈为空！" << endl;
		return -1;
	}
	int temp = S.Sacklist[S.top];
	S.top--;
	return temp;
}

//返回结点在结点数组中的下标
int Location(GraphList &G, int key) {
	for (int i = 0; i < G.vexnum; i++) {
		if (G.arclist[i].data == key) {
			return i;
		}
	}
	return -1;
}

//创建图
void CreatGraph(GraphList &G) {
	cout << "请输入顶点数：" << endl;
	cin >> G.vexnum;
	cout << "请输入顶点信息：" << endl;
	for (int i = 0; i < G.vexnum; i++) {
		cin >> G.arclist[i].data;
	}
	cout << "请输入弧数：" << endl;
	cin >> G.arcnum;
	cout << "请输入弧端点信息：" << endl;
	for (int i = 0; i < G.arcnum; i++) {
		int v1, v2;
		cin >> v1 >> v2;
		int Location1 = Location(G, v1);
		int Location2 = Location(G, v2);
		VexNode *new_node = new VexNode;
		new_node->data = Location2;
		new_node->next = G.arclist[Location1].firstacr;
		G.arclist[Location1].firstacr = new_node;
		indegree[Location2]++;
	}
}

//拓扑排序
int TopoSort(GraphList &G, int *topolist) {
	Stack S;
	int topo = 0;
	//先将所有入度为0的结点入栈
	for (int i = 0; i < G.vexnum; i++) {
		if (indegree[i] == 0) {
			Push(S, i);
		}
	}
	//依次出栈入度为0的结点
	while (S.top != -1) {
		int vx = Pop(S);
		topolist[topo++] = G.arclist[vx].data;	//输出结点
		VexNode *temp = G.arclist[vx].firstacr;
		//删除以该结点为尾的弧
		while (temp != NULL) {
			int index = temp->data;
			indegree[index]--;	//将该弧的弧头结点入度减1
			//如果入度为0，则入栈
			if (indegree[index] == 0) {
				Push(S, index);
			}
			temp = temp->next;
		}
	}
	topolist[topo] = -1;
	//如果拓扑序列中的元素个数等于所有元素个数，则该图无环，否则该图有环
	if (topo == G.vexnum) {
		return OK;
	} else {
		return ERROR;
	}
}

int main() {
	GraphList GL;
	CreatGraph(GL);
	int topolist[MAXVERTIES] = { 0 };
	int vx = TopoSort(GL, topolist);
	if (!vx) {
		cout << "有环！" << endl;
	} else {
		cout << "有向无环！" << endl;
		cout << "拓扑序列如下：" << endl;
		for (int i = 0; topolist[i] != -1; i++) {
			cout << topolist[i] << " ";
		}
	}
	return 0;
}

如果大家有什么问题的话，欢迎在下方评论区进行讨论哦~

【上一讲】图 - 04 最短路径
【下一讲】图 - 06 关键路径