拓扑排序详解及C++实现

拓扑排序详解及C++实现

定义

百度百科定义如下：

拓扑排序，是对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

很显然这一段话不是人话十分晦涩难懂，令人深思。

有向无环图

图论基础知识可以参考图论（一）基本概念_图论是什么_翟羽嚄的博客-CSDN博客。

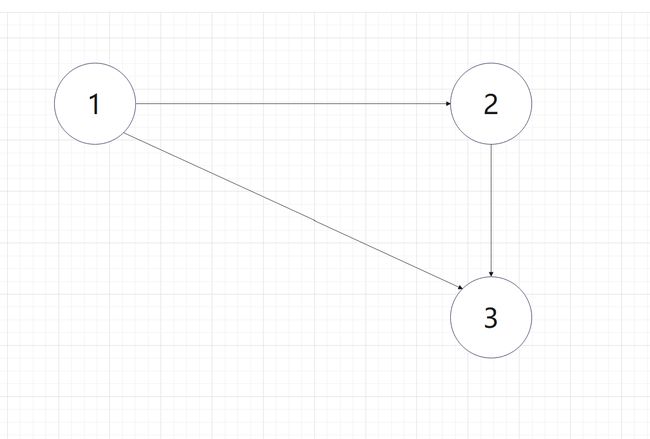
需要注意：有向无环图不一定是树，例如：

拓扑序列

对于一个有向无环图将图中的顶点排成一个序列，其中每个边的起点在序列中一定在终点之前；

（↑↑ 不是人话

通俗一点解释为：将一张图“压扁”，使顶点从左到右排成序列，且压扁后每条边的方向只能朝右，那么这个序列是这张图的拓扑序列。

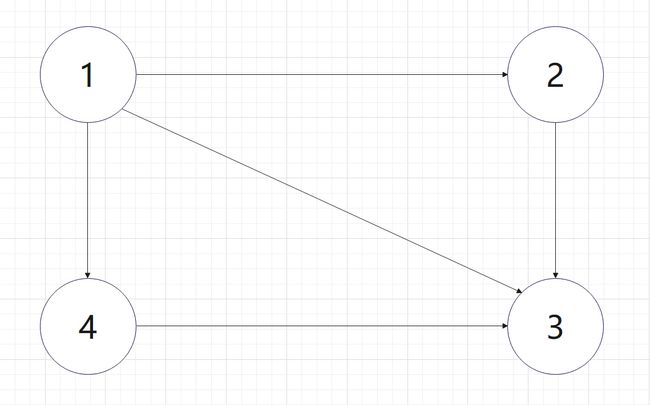
例如这张图：

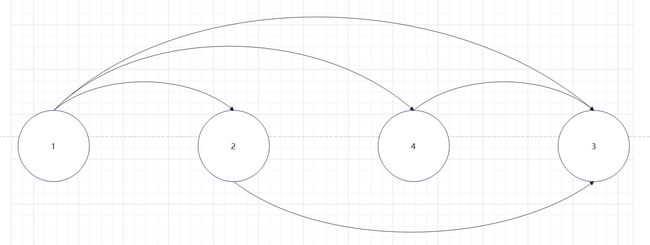
其拓扑序列为1-2-4-3：

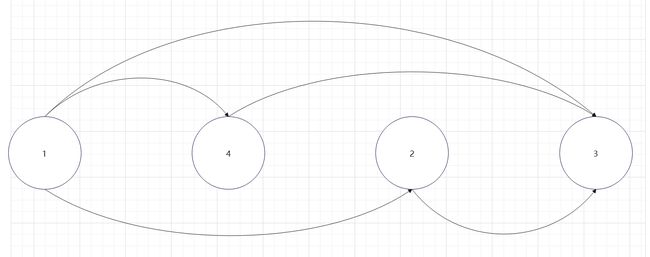
对于同一张图，可能存在不止一个拓扑序列。例如上图的另一个拓扑序列为1-4-2-3：

拓扑排序

那么拓扑排序可表示为：计算一个有向无环图的拓扑序列。

逻辑

拓扑排序的逻辑如下：

1. 集合$S$表示所有入度为0的点；队列$L$表示拓扑序列。初始时为空。
2. 找到所有入度为0的点，放入$S$中。
3. 从$S$中取出一个点$u$，放入$L$中。
4. 在图中删除$s$，并删除所有以$s$为起点的边。
5. 重复2~4，直到$S$为空。

---

手动模拟拓扑排序的步骤如下：

手动模拟内容较长，如已经理解可以跳过

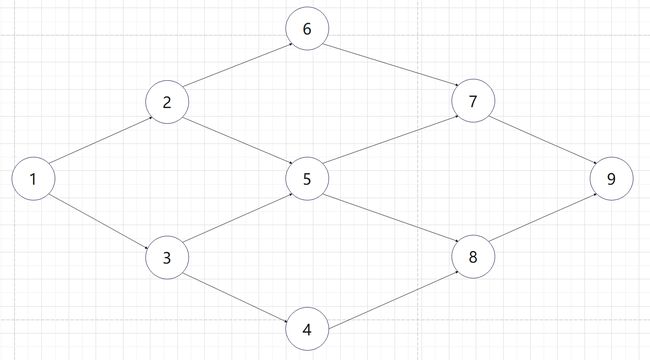
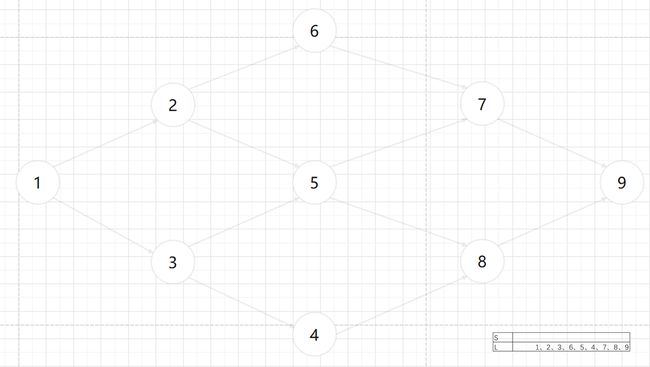
对于这张图：

其中入度为0的点为1，因此$S$和$L$初始化如下：

将1从$S$中取出并放入$L$：

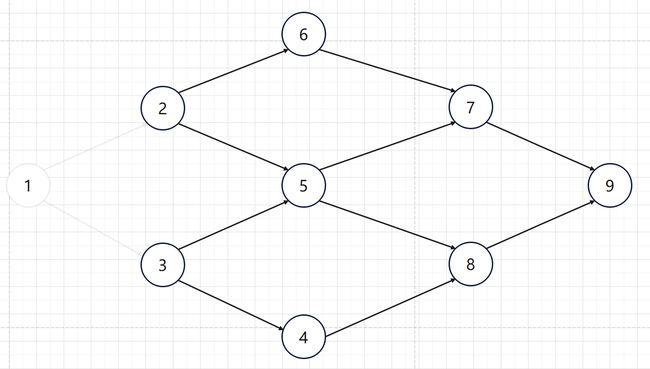
删除点1和所有以1为起点的边：

此时2和3的入度更新为0，所以将2和3放入$S$：

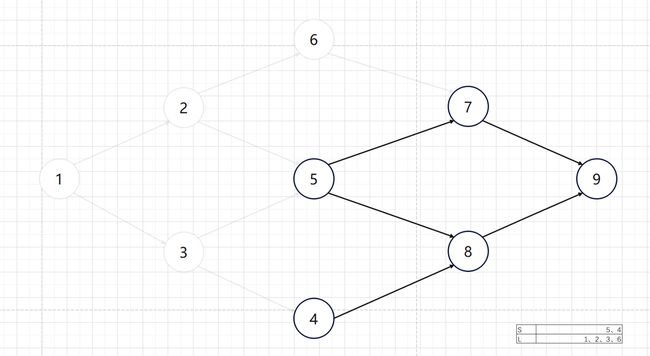
重复上述步骤。将2从$S$中取出、放入$L$；删除2和以2为起点的边；将6推入队列：

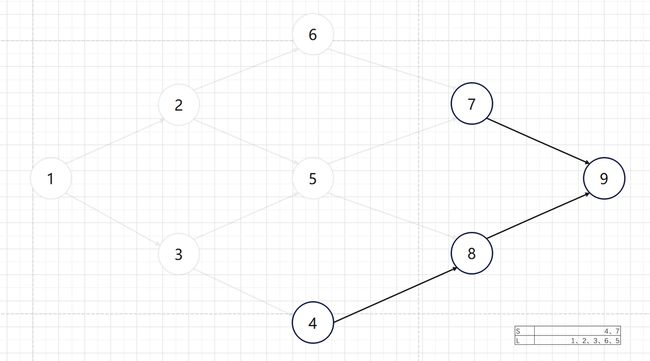
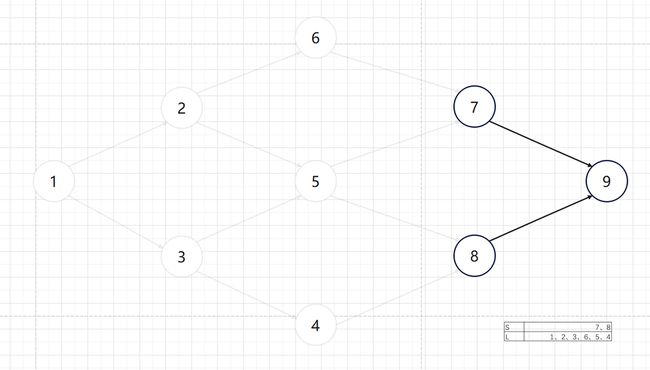
继续重复此步骤，分别从$S$中取3、6、5、4、7、8、9

此时$S$为空，所以结束计算。

拓扑序列为1 2 3 6 5 4 7 8 9：

代码实现

读入部分

使用链式向前星储存图：

struct edge
{
	int to;
	int next;
};

int head[100005];
edge graph[100005];
int n, m;

读入图：

cin >> n >> m;
for (int i = 1; i <= m; i++)
{
	int s, e;
	cin >> s >> e;

	graph[i].next = head[s];
	graph[i].to = e;
	head[s] = i;
}

由于需要计算点的入度，因此使用d数组储存节点的入度：

int d[100005];

在读入图时计算：

d[e]++;

读图部分完整代码为

#include 
using namespace std;

struct edge
{
	int to;
	int next;
};

int head[100005];
edge graph[100005];
int d[100005];
int n, m;

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int s, e;
		cin >> s >> e;

		graph[i].next = head[s];
		graph[i].to = e;
		head[s] = i;
		d[e]++;
	}
}

拓扑排序部分

使用队列que储存集合$S$：

queue<int> que;

遍历$1\sim N$，将入度为0（d[i] == 0）的点插入队列：

for (int i = 1; i <= n; i++)
{
	if (d[i] == 0)
	{
		que.push(i);
	}
}

当que不为空时，从que中取出一个点$u$，并输出（加入拓扑序列$L$）

while (!que.empty())
{
	int now = que.front();
	que.pop();
	cout << now << " ";
}

删除所有以$u$为起点的边；实现时不需要真正从图中删除，直接将终点的入度减1即可：

for (int i = head[now]; i != 0; i = graph[i].next)
{
	d[graph[i].to]--;
}

如果某个点的入度更新后变为0，那么将这个点推入que：

for (int i = head[now]; i != 0; i = graph[i].next)
{
	d[graph[i].to]--;
	if (d[graph[i].to] == 0)
	{
		que.push(graph[i].to);
	}
}

拓扑排序部分完整代码为：

...

queue<int> que;

...

int main()
{
	...

	while (!que.empty())
	{
		int now = que.front();
		que.pop();
		cnt--;
		cout << now << " ";
		for (int i = head[now]; i != 0; i = graph[i].next)
		{
			d[graph[i].to]--;
			if (d[graph[i].to] == 0)
			{
				que.push(graph[i].to);
			}
		}
	}
}

拓扑排序判环

上文中提到拓扑排序的只能对有向无环图进行排序。

如果图中出现环，则$S$为空时图不为空。

利用这个特点，可以判断有向图中是否存在环。

使用cnt变量计算que中的元素数量（出队元素数量）：

...
int main()
{
	...
	
	int cnt = n;

	while (!que.empty())
    ...
}

每出队一个元素，cnt--：

while (!que.empty())
{
	int now = que.front();
	que.pop();
	
	cnt--;
	
	...
}

如果计算结束后图不为空，即cnt > 0，则图中有环：

if (cnt) // cnt > 0
{
	cout << "Circle!" << endl;
}

完整代码

#include 
#include 
using namespace std;

struct edge
{
	int to;
	int next;
};

int head[100005];
edge graph[100005];

int d[100005];
int n, m;

queue<int> que;

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int s, e;
		cin >> s >> e;

		graph[i].next = head[s];
		graph[i].to = e;
		head[s] = i;
		d[e]++;
	}

	for (int i = 1; i <= n; i++)
	{
		if (d[i] == 0)
		{
			que.push(i);
		}
	}

	int cnt = n;

	while (!que.empty())
	{
		int now = que.front();
		que.pop();
		cnt--;
		cout << now << " ";
		for (int i = head[now]; i != 0; i = graph[i].next)
		{
			d[graph[i].to]--;
			if (d[graph[i].to] == 0)
			{
				que.push(graph[i].to);
			}
		}
	}

	cout << endl;
	if (cnt)
	{
		cout << "Circle!" << endl;
	}
}