【Matlab】创建连续时间模型(控制系统工具箱)
本节用tf, zpk, ss, 和 frd命令来创建连续时间模型。
文章目录
-
- LTI线性时不变模型
- 创建传递函数模型
- 创建零极点增益模型
- 创建状态空间模型
- 创建频率响应数据模型
- 创建MIMO(多输入多输出模型)
- 分析LTI(线性时不变模型)
LTI线性时不变模型
控制系统工具箱™提供了用于创建线性时不变 (LTI) 模型的四个基本表示形式的函数:
- 传递函数 (TF) 模型
- 零极点增益 (ZPK) 型号
- 状态空间 (SS) 模型
- 频率响应数据 (FRD) 模型
将模型数据作为输入,这些函数就能创建对应的模型对象。
创建传递函数模型
传递函数(TF)是LTI系统的频域表示。SISO(single input single output,单输入单输出) 传递函数可以用多项式表示:
H ( s ) = A ( s ) B ( s ) = a 1 s n + a 2 s n − 1 + … + a n + 1 b 1 s m + b 2 s m − 1 + … + b m + 1 H(s) = \frac{A(s)}{B(s)} = \frac{a_{1} s^{n} + a_{2} s^{n-1} + \ldots + a_{n+1}}{b_{1} s^{m} + b_{2} s^{m-1} + \ldots + b_{m+1}} H(s)=B(s)A(s)=b1sm+b2sm−1+…+bm+1a1sn+a2sn−1+…+an+1
传递函数由其分子和分母多项式指定,并且 。在 MATLAB 中,多项式由其系数的向量表示,例如,多项式: s 2 + 2 s + 10 s^{2} + 2 s + 10 s2+2s+10,是由[1 2 10]表示的。
要创建以下表示传递函数的 TF 对象:
H ( s ) = s s 2 + 2 s + 10 H(s) = \frac{s}{s^2+2s+10} H(s)=s2+2s+10s
用代码表示如下:
num = [ 1 0 ]; % Numerator: s
den = [ 1 2 10 ]; % Denominator: s^2 + 2 s + 10
H = tf(num,den)
生成传递函数如下:
或者用下列表达式来表示该模型:
s = tf('s'); % Create Laplace variable 创建拉普拉斯变量
H = s / (s^2 + 2*s + 10)
会生成同样的传递函数:
创建零极点增益模型
零极点增益 (ZPK) 模型是传递函数的因式相乘形式:
H ( s ) = k ( s − z 1 ) … ( s − z n ) ( s − p 1 ) … ( s − p m ) H(s) = k \frac{( s - z_{1} ) \ldots ( s - z_{n} )}{( s - p_{1} ) \ldots ( s - p_{m} )} H(s)=k(s−p1)…(s−pm)(s−z1)…(s−zn)
在这个式子中,k为增益,分子的根为零点,分母的根为极点。
比如要创建这个零极点增益模型:
H ( s ) = − 2 s ( s − 2 ) ( s 2 − 2 s + 2 ) H(s) = \frac{-2 s}{( s - 2 ) ( s^2 - 2 s + 2 )} H(s)=(s−2)(s2−2s+2)−2s
指定零极点和增益如下:
z = 0; % Zeros
p = [ 2 1+i 1-i ]; % Poles
k = -2; % Gain
H = zpk(z,p,k)
生成模型如下:
s = zpk('s');
H = -2*s / (s - 2) / (s^2 - 2*s + 2)
生成结果同上:
创建状态空间模型
状态空间 (State-space,SS) 模型是 LTI 系统的时域表示:
d x d t = A x ( t ) + B u ( t ) \frac{dx}{dt} = A x(t) + B u(t) dtdx=Ax(t)+Bu(t)
y ( t ) = C x ( t ) + D u ( t ) y(t) = Cx(t) + Du(t) y(t)=Cx(t)+Du(t)
其中,x(t)是状态向量,u(t)是输入向量,y(t)是输出轨迹。
状态空间模型是从描述系统动力学的微分方程推导出来的。例如,考虑一个简单电机的二阶常微分方程(ODE):
d 2 θ d t 2 + 2 d θ d t + 5 θ = 3 I \frac{d^2\theta}{dt^2} + 2\frac{d\theta}{dt} + 5\theta = 3I dt2d2θ+2dtdθ+5θ=3I
其中,I是驱动电流(输入),theta是转子角度(输出)。此 ODE 可以以状态空间形式重写为:
d x d t = A x + B I \frac{dx}{dt} = Ax + BI dtdx=Ax+BI

θ = C x + D I \theta = Cx + DI θ=Cx+DI
![]()
要创建此模型,创建ss状态空间矩阵并定义A、B、C、D即可。
A = [ 0 1 ; -5 -2 ];
B = [ 0 ; 3 ];
C = [ 1 0 ];
D = 0;
H = ss(A,B,C,D)
生成结果如下:
创建频率响应数据模型
频率响应数据 (FRD) 模型允许您将系统的测量或仿真的复杂频率响应存储在 LTI 对象中。然后,可以将此数据用作频域分析和设计目的的替代模型。
例如,假设从频率分析器中获取以下数据:
频率(赫兹): 10, 30, 50, 100, 500
响应: 0.0021+0.0009i, 0.0027+0.0029i, 0.0044+0.0052i, 0.0200-0.0040i,0.0001-0.0021i
可以使用以下命令创建包含此数据的 FRD 对象:
freq = [10, 30, 50, 100, 500];
resp = [0.0021+0.0009i, 0.0027+0.0029i, 0.0044+0.0052i, 0.0200-0.0040i, 0.0001-0.0021i];
H = frd(resp,freq,'Units','Hz')
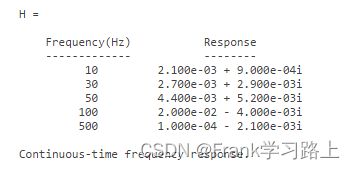
结果如下:
频率单位为rad/s。
创建MIMO(多输入多输出模型)
tf, zpk, ss, 和 frd命令可以创建SISO 和 MIMO 两种模型。对于 TF 或 ZPK 模型,通过连接更简单的 SISO 模型来构造 MIMO 模型通常很方便。例如,可以创建 2x2 MIMO 传递函数:
H ( s ) = [ 1 s + 1 0 s + 1 s 2 + s + 3 − 4 s s + 2 ] H(s) = \left[ \begin{array}{cc} {1\over s+1} & 0 \\ & \\ {s+1 \over s^2+s+3} & {-4s \over s+2} \end{array} \right] H(s)=⎣ ⎡s+11s2+s+3s+10s+2−4s⎦ ⎤
用以下代码表示:
s = tf('s');
H = [ 1/(s+1) , 0 ; (s+1)/(s^2+s+3) , -4*s/(s+2) ]
生成结果如下:
分析LTI(线性时不变模型)
控制系统工具箱可以用于分析 LTI 模型。这些功能的范围从简单的I/O大小和顺序查询到复杂的时间和频率响应分析。
例如,可以获取上面指定的 MIMO 传输函数的大小信息:
size(H)
![]()
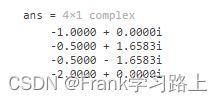
可以使用以下公式计算极点:
pole(H)
可以使用以下命令询问此系统是否稳定:
isstable(H)
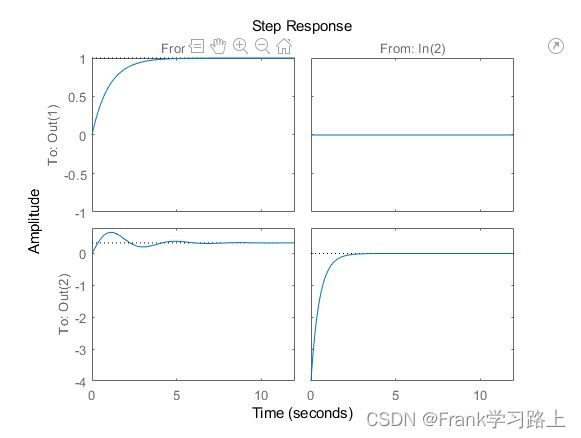
最后,可以通过键入以下内容来绘制阶跃响应:
step(H)
以上。