【算法】动态规划 && leetcode (递推、斐波那契数变体、打家劫舍问题)
目录
- 动态规划理解
-
- 递推
-
- 题目 - 数字三角形
- 总结
-
- 路径问题
- 斐波那契数变体
-
- 骨牌问题
- 兔子产子问题
- 打家劫舍问题
-
- 198. 打家劫舍
- 213. 打家劫舍 II
- 337. 打家劫舍 III
- 740. 删除并获得点数
- 简单
-
- 509. 斐波那契数
- 70. 爬楼梯
- 746. 使用最小花费爬楼梯
- 53. 最大子序和 (\*)
- 674. 最长连续递增序列
-
- 贪心法
- 中等
-
- 322. 零钱兑换 \*\*\*
- 516. 最长回文子序列 \*\*\*
- 62. 不同路径 \*\*
- 63. 不同路径 II
- 343. 整数拆分(难)
- 96. 不同的二叉搜索树 hard
- 494. 目标和 ??
- 300. 最长递增子序列
- 718. 最长重复子数组
-
- 滑动窗口
- 1143. 最长公共子序列 ***
- 1035. 不相交的线
- 647. 回文子串 (***)
-
- 双指针法 ***
- 516. 最长回文子序列(难)
- 139. 单词拆分
- 剑指 Offer II 091. 粉刷房子
- 873. 最长的斐波那契子序列的长度
- 困难
-
- 1312. 让字符串成为回文串的最少插入次数 \*\*\*
动态规划理解
【参考:【蓝桥杯】最难算法没有之一· 动态规划真的这么好理解?_安然无虞的博客-CSDN 博客】
动态规划(英语:Dynamic programming,简称 DP),通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 (是不是很像前面讲解过的一种算法——分治,其实可以认为动态规划就是特殊的分治)
动态规划常常适用于有重叠子问题和最优子结构性质的问题,并且会记录所有子问题的结果,因此动态规划方法所耗时间往往远少于暴力递归解法。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化搜索,自底向上就是递推。
记忆化搜索是用搜索的方式实现了动态规划,因此记忆化搜索就是动态规划。
提问:
何为记忆化搜索?
回答:
顾名思义,记忆化搜索肯定也就和“搜索”脱不了关系, 前面讲解的递归、DFS 和 BFS 想必大家都已经掌握的差不多了,它们有个最大的弊病就是:低效!原因在于没有很好地处理重叠子问题。
那么对于记忆化搜索呢,它虽然采用搜索的形式,但是它还有动态规划里面递推的思想,巧就巧在它将这两种方法很好的综合在了一起,简单又实用。
记忆化搜索,也叫记忆化递归,其实就是拆分子问题的时候,发现有很多重复子问题,然后再求解它们以后记录下来。以后再遇到要求解同样规模的子问题的时候,直接读取答案。
啥叫「自顶向下」?递归
注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 f(20),向下逐渐分解,直至 f(1) 和 f(2) 这两个 base case,然后逐层返回答案,这就叫「自顶向下」。
啥叫「自底向上」?循环迭代
反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(20),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
比如斐波那契数列,青蛙跳台阶除了暴力递归就是用循环迭代dp[i] = dp[i - 1] + dp[i - 2];
递推
递推
从问题出发逐步推到已知条件,此种方法叫逆推
递推和递归非常相似。
递推是把问题划分为若干个步骤,每个步骤之间,或者是这个步骤与之前的几个步骤之间有一定的数量关系,可以用前几项的值表示出这一项的值,这样就可以把一个复杂的问题变成很多小的问题。
递推算法注意的是设置什么样的递推状态,因为一个好的递推状态可以让问题很简单。最难的是想出递推公式,一般递推公式是从后面向前想,倒推回去。
总结:从多推向少 因为 dp[i][j]需要比较多的初始条件
- 起点有一个,终点有多个:从终点往起点推
- 数字三角形
- 起点有一个,终点有一个:从起点往终点推或者从终点往起点推都可以
- 62. 不同路径 - 力扣(LeetCode)
题目 - 数字三角形
【参考:P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles - 洛谷】

正常思路都是从最高处往下走,可递推需要从最低处往上走
思路:
本题采用倒推的方式:
假设dp[i][j]表示的是从最底部到 i, j 的最大路径之和,也可以说是从 i, j 到最后一层的最大路径之和,前面那种好理解一点
i: [ r-1,0 ] ,i - -;
当从顶层沿某条路径走到第 i+1 层向第 i 层前进(向上)时,我们的选择是沿两条可行路径中最大数字的方向前进(左上角或右上角),所以找出递推关系:dp[i][j] = nums[i][j] + max(dp[i+1][j],dp[i+1][j+1])
注意:dp[i][j]表示当前数字的值,dp[i+1][j]和dp[i+1][j+1]分别表示从最底部到 i+1,j、i+1,j+1 的最大路径之和;
最终 dp[0][0]就是所求
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int r = sc.nextInt();
int[][] nums = new int[r][r];
for (int i = 0; i < r; i++) {
for (int j = 0; j <= i; j++) {
nums[i][j] = sc.nextInt();
}
}
int[][] dp = new int[r][r];
// 初始化
for (int i = 0; i < r; i++) {
dp[r-1][i]=nums[r-1][i]; // 最底层就是nums[r-1][i]本身
}
// 从倒数第二层开始遍历直到最顶部
for (int i = r - 2; i >=0; i--) {
for (int j = 0; j <= i; j++) {
// 当前元素 + 下面左右两个dp的最大值
dp[i][j] = nums[i][j] + Math.max(dp[i + 1][j], dp[i + 1][j + 1]);
}
}
System.out.println(dp[0][0]);
}
}
简化版
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int r = sc.nextInt();
int[][] dp = new int[r][r];
for (int i = 0; i < r; i++) {
for (int j = 0; j <= i; j++) {
dp[i][j] = sc.nextInt();
}
}
// 初始化
// 最底层就是dp[r-1][]本身
for (int i = r - 2; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[i][j] = dp[i][j] + Math.max(dp[i + 1][j], dp[i + 1][j + 1]);
}
}
System.out.println(dp[0][0]);
}
}
总结
多种方法 (*)
推导公式,得出递推关系
- 1.先暴力递归
- 2.然后使用带备忘录 memo 进行递归(记忆化递归)
- 3.动态规划 dp
memo 数组和 dp 数组的内容是一样的,只不过把递归换成了 for 循环迭代了而已
注意看 509、332 题
路径问题
注意 dp[][] 初始化,尤其是第一行和第一列
斐波那契数变体
- 爬楼梯、青蛙跳台阶
骨牌问题
【参考:hdoj2046 骨牌铺方格题解+拓展(递推/斐波那契)_Cassie_zkq 的博客-CSDN 博客】
1).先铺前 n-1 列,则有 f(n-1)种方法,对于第 n 列,则只有竖着铺一种方法,方法数为 f(n-1)
2).先铺前 n-2 列,则有 f(n-2)种方法,对于第 n-1 列和第 n 列,如果两个都竖着铺则和 1)中铺的方法有重复,所以只能横着铺,方法数为 f(n-2)
所以递推公式:f(n)=f(n-1)+f(n-2) ,会惊奇的发现,这就是斐波那契数列。
然后使用初始的几种情况进行验证即可
n = 1 时,只有一种铺法
n = 2 时,如下图,有全部竖着铺和横着铺两种
n = 3 时,骨牌可以全部竖着铺,也可以认为在方格中已经有一个竖铺的骨牌,则需要在方格中排列两个横排骨牌(无重复方法),若已经在方格中排列两个横排骨牌,则必须在方格中排列一个竖排骨牌。如下图,再无其他排列方法,因此铺法总数表示为三种。
通过上面的分析,不难看出规律:f(3) = f(1) + f(2)
所以可以的得到递推关系:f(n) = f(n - 1) + f(n - 2)
同理可以分析,1)先铺前 n-1 个格子,第 n 个格子只能放 1×1,所以总的方法数为 f(n-1)
先铺前 n-2 个格子,第 n 和 n-1 个格子只能放 1×2 的(如果放两个 1x1 的 会和 1)重复,因为 1)包括了这种情况),所以总的方法数为 f(n-2)
同理可得先铺前 n-3 个格子,总的方法数为 f(n-3)
所以 f(n)=f(n-1)+f(n-2)+f(n-3)
【参考:递推算法-五种典型的递推关系_lybc2019 的博客-CSDN 博客】
兔子产子问题
把雌雄各一的一对新兔子放入养殖场中。每只雌兔在出生两个月以后,每月产雌雄各一的一对新兔子。试问第 n 个月后养殖场中共有多少对兔子。
第 1 个月:一对新兔子 r1。用小写字母表示新兔子。
第 2 个月:还是一对新兔子,不过已经长大,具备生育能力了,用大写字母 R1 表示。
第 3 个月:R1 生了一对新兔子 r2,一共 2 对。
第 4 个月:R1 又生一对新兔子 r3,一共 3 对。另外,r2 长大了,变成 R2。
第 5 个月:R1 和 R2 各生一对,记为 r4 和 r5,共 5 对。此外,r3 长成 R3。
第 6 个月:R1、R2 和 R3 各生一对,记为 r6 ~ r8,共 8 对。此外,r4 和 r5 长大。
……
把这些数排列起来:1,1,2,3,5,8,……,事实上,可以直接推导出来递推关系 f(n)=f(n-1)+f(n-2):第 n 个月的兔子由两部分组成,一部分是上个月就有的老兔子 f(n-1),一部分是这个月出生的新兔子 f(n-2)(第 n 个月时具有生育能力的兔子数就等于第 n-2 个月兔子总数)。根据加法原理,f(n)=f(n-1)+f(n-2)。
解:设满 x 个月共有兔子 Fx 对,其中当月新生的兔子数目为 Nx 对。第 x-1 个月留下的兔子数目设为 F(x-1)对。则:
Fx=Nx+ Fx-1
Nx=F(x-2 ) (即第 x-2 个月的所有兔子到第 x 个月都有繁殖能力了)
∴ Fx=F(x-1)+F(x-2 ) 边界条件:F0=0,F1=1
由上面的递推关系可依次得到
F2=F1+F0=1,F3=F2+F1=2,F4=F3+F2=3,F5=F4+F3=5,……。
Fabonacci 数列常出现在比较简单的组合计数问题中,例如以前的竞赛中出现的“骨牌覆盖”问题。在优选法中,Fibonacci 数列的用处也得到了较好的体现。
打家劫舍问题
【参考:经典动态规划:打家劫舍系列问题labuladong微信公众号】
198. 打家劫舍
【参考:198. 打家劫舍 - 力扣(LeetCode)】
class Solution {
public int rob(int[] nums) {
int n=nums.length;
// 边界情况
if(n==1){
return nums[0];
}
if(n==2){
return Math.max(nums[0],nums[1]);
}
// dp[i]表示 偷第0-i间房屋所得的最大金额
int[] dp=new int[n];
Arrays.fill(dp,-1);// 0 <= nums[i] <= 400
dp[0]=nums[0];
dp[1] = Math.max(nums[0], nums[1]); // 注意这里
for(int i=2;i<n;i++){
// 不偷,偷
dp[i]=Math.max(dp[i-1],nums[i]+dp[i-2]);
}
return dp[n-1];
}
}
labuladong
从后往前遍历
int rob(int[] nums) {
int n = nums.length;
// dp[i] = x 表示:dp[x..] 能抢到的最大值
// 从第 i 间房子开始抢劫,最多能抢到的钱为 x
// base case: dp[n] = 0
int[] dp = new int[n + 2];
for (int i = n - 1; i >= 0; i--) {
dp[i] = Math.max(dp[i + 1], nums[i] + dp[i + 2]);
}
return dp[0];
}
213. 打家劫舍 II
【参考:213. 打家劫舍 II - 力扣(LeetCode)】
所有的房屋都 围成一圈
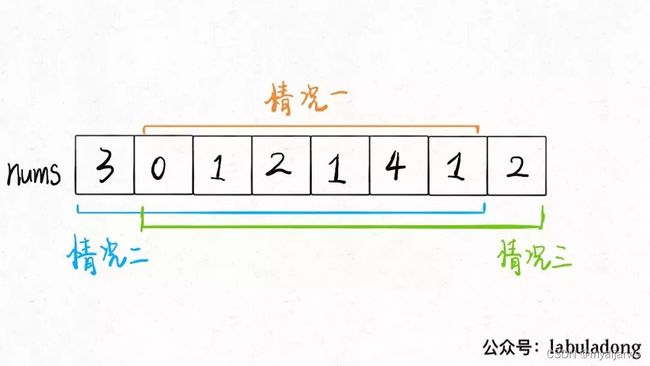
如果不偷窃最后一间房屋,则偷窃房屋的下标范围是 [ 0 , n − 2 ] [0,n−2] [0,n−2];如果不偷窃第一间房屋,则偷窃房屋的下标范围是 [ 1 , n − 1 ] [1, n-1] [1,n−1]。
class Solution {
public int rob(int[] nums) {
int n=nums.length;
// 边界情况
if(n==1){
return nums[0];
}
if(n==2){
return Math.max(nums[0],nums[1]);
}
return Math.max(robRange(nums,1,n),
robRange(nums,0,n-1));
}
public static int robRange(int[] nums,int start,int end) {
int n=nums.length;
// dp[i]表示 偷第0-i间房屋所得的最大金额
int[] dp=new int[n];
Arrays.fill(dp,-1);// 0 <= nums[i] <= 400
dp[start]=nums[start];
dp[start+1] = Math.max(nums[start], nums[start+1]); // 注意这里
for(int i=start+2;i<end;i++){
// 不偷,偷
dp[i]=Math.max(dp[i-1],nums[i]+dp[i-2]);
}
return dp[end-1];
}
}
337. 打家劫舍 III
【参考:337. 打家劫舍 III - 力扣(LeetCode)】
由于二叉树不适合拿数组当缓存,我们这次使用哈希表来存储结果,TreeNode 当做 key,能偷的钱当做 value
【参考:三种方法解决树形动态规划问题-从入门级代码到高效树形动态规划代码实现 - 打家劫舍 III - 力扣(LeetCode)】这篇写的不错
class Solution {
Map<TreeNode,Integer> memo=new HashMap<>();
public int rob(TreeNode root) {
if(root==null) return 0;
// 利用备忘录消除重叠子问题
if(memo.containsKey(root))
return memo.get(root);
// 抢,然后去下下家
int doit=root.val;
if(root.left!=null){
doit+=rob(root.left.left)+rob(root.left.right);
}
if(root.right!=null){
doit+=rob(root.right.left)+rob(root.right.right);
}
// 不抢,然后去下家
int notdo=rob(root.left)+rob(root.right);
int result=Math.max(doit,notdo);
memo.put(root,result);
return result;
}
}
740. 删除并获得点数
【参考:740. 删除并获得点数 - 力扣(LeetCode)】
打家劫舍变体
【参考:如果你理解了《打家劫舍》,这题你肯定会 - 删除并获得点数 - 力扣(LeetCode)】
class Solution:
def deleteAndEarn(self, nums) -> int:
N = len(nums)
M = max(nums) # 最大的数
all = [0] * (M + 1)
for x in nums:
all[x] += 1 # 数字x为下标,个数为值
# dp[i]表示 偷第0-i间房屋所得的最大点数
dp = [0] * (M + 1)
# 初始化
dp[0] = all[0] * 0 # 0
dp[1] = all[1] * 1
for i in range(2, M+1):
dp[i] = max(i * all[i] + dp[i - 2], # 选当前数字i + 选择i-2位置的得到最大点数
dp[i - 1]) # 不选当前数字i + 选择i-1位置的得到最大点数
return dp[M]
简单
509. 斐波那契数
【参考: 509. 斐波那契数- 力扣(LeetCode)】
class Solution {
// 动态规划的四个步骤
public int fib(int n) {
if (n <= 1) return n;
// 1. 定义状态数组,dp[i] 表示的是数字 i 的斐波那契数
int[] dp = new int[n + 1];
// 2. 状态初始化
dp[0] = 0;
dp[1] = 1;
// 3. 状态转移
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
// 4. 返回最终需要的状态值
return dp[n];
}
}
当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就行了
class Solution {
public int fib(int n) {
if (n == 0 || n == 1) {
// base case
return n;
}
// 分别代表 dp[i - 1] 和 dp[i - 2]
int dp_i_1 = 1, dp_i_2 = 0;
for (int i = 2; i <= n; i++) {
// dp[i] = dp[i - 1] + dp[i - 2];
int dp_i = dp_i_1 + dp_i_2;
// 滚动更新
dp_i_2 = dp_i_1;
dp_i_1 = dp_i;
}
return dp_i_1;
}}
/*
理解
dp_i_2 dp_i_1 dp_i
↓ ↓
dp_i_2 dp_i_1 dp_i
返回 dp_i_1
*/
class Solution {
public int fib(int n) {
if (n < 1) return 0;
if (n == 2 || n == 1)
return 1;
int prev = 1, cur = 1;
for (int i = 3; i <= n; i++) {
int sum = prev + cur;
prev = cur;
cur = sum;
}
return curr;
}
}
/*
理解
prev cur sum
↓ ↓
prev cur sum
返回 cur
*/
70. 爬楼梯
【参考:70. 爬楼梯 - 力扣(LeetCode)】
//暴力
public int climbStairs(int n) {
if (n == 1)
return 1;
if (n == 2)
return 2;
return climbStairs(n-1)+climbStairs(n-2);
}
// memo
class Solution {
int[] memo;
public int climbStairs(int n) {
if (n == 1)
return 1;
if (n == 2)
return 2;
memo=new int[n+1];// 默认初始化为0
memo[0]=1;
memo[1]=1;
return helper(n);
}
public int helper(int n) {
if(memo[n]!=0)
return memo[n];
else
memo[n]=helper(n-1)+helper(n-2);
return memo[n];
}
}
// dp
public int climbStairs(int n) {
if (n == 1)
return 1;
if (n == 2)
return 2;
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
746. 使用最小花费爬楼梯
【参考:746. 使用最小花费爬楼梯 - 力扣(LeetCode)】
题目描述有问题
可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯
即选择地面或者第一级台阶作为起点
____楼顶_____________________
_3_|
_2_|
_1_| 第一级台阶
_0_| 地面
///
class Solution {
public int minCostClimbingStairs(int[] cost) {
int len=cost.length;
// dp[i] 表示达到第i级台阶的最小花费
int[] dp=new int[len+1];
dp[0]=0;// 把地面作为起点(还没上台阶,还在地面,所以没有花费)
dp[1]=0;// 把第一个台阶作为起点并走到第一个台阶(不用动,所以没有花费)
for(int i=2;i<=len;i++){
dp[i]=Math.min(dp[i-1]+cost[i-1],
dp[i-2]+cost[i-2]);
}
return dp[len];
}
}
53. 最大子序和 (*)
暴力法
public static int maxSum_1(int[] arr) {
int sum = 0;
int i, j, k;
for (i = 0; i < arr.length; i++) { //子序列起始位置
for (j = i + 1; j < arr.length; j++) { //子序列终止位置
int thisSum = 0; //当前子段的和
for (k = i; k <= j; k++) // 计算下标i到j之间数的和
thisSum += arr[k];
if (thisSum > sum)
sum = thisSum;
}
}
return sum;
}
// 思想:直接在划定子序列时累加元素值,减少一层循环。
public static int maxSum_2(int[] arr) {
int sum = 0;
int i, j;
for (i = 0; i < arr.length; i++) { //子序列起始位置
int thisSum = 0; //当前子段的和
for (j = i; j < arr.length; j++) {
thisSum += arr[j];
if (thisSum > sum)
sum = thisSum;
}
}
return sum;
}
分治法
// 将序列划分为左右两部分,则最大子段和可能在三处出现:左半部、右半部以及跨越左右边界的部分。
// 递归的终止条件是:left == right
public static int maxSum_3(int[] arr, int left, int right) {
if (left == right) //如果序列长度为1,直接求解
return Math.max(arr[left], 0); // arr[left]值为负数返回0
int center = (left + right) / 2;
// 递归
int leftSum = maxSum_3(arr, left, center); // 求左半部分最大子段和
int rightSum = maxSum_3(arr, center + 1, right); // 求右半部分最大子段和
int s1 = 0;
int leftTemp = 0;
for (int i = center; i >= left; i--) { // left <= center 求最大子段和
leftTemp += arr[i];
if (leftTemp > s1)
s1 = leftTemp; //左边最大值赋值给s1
}
int s2 = 0;
int rightTemp = 0;
for (int j = center + 1; j <= right; j++) { // center => right 求最大子段和
rightTemp += arr[j];
if (rightTemp > s2)
s2 = rightTemp; //右边最大值赋值给s2
}
int sum = s1 + s2; // 跨边界center的最大子段和
return Math.max(sum, Math.max(leftSum, rightSum)); // 取最大值
}
动态规划
// dp[i]:以nums[i]结尾的“最大子段和”
public static int maxSum_4(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
int[] dp = new int[n];
dp[0] = nums[0];
// 状态转移方程
for (int i = 1; i < n; i++) {
// dp要么和前面相邻的子段连接,要么自成一派
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
}
int sum = 0;
// 取最大值
for (int i = 0; i < n; i++) {
sum = Math.max(dp[i], sum);
}
return sum;
}
public static int maxSum_5(int[] nums) {
if (nums.length == 0) return 0;
int sum = 0; // 子段和
int result = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
if (sum > result) // 取区间累计的最大值
result = sum;
if (sum < 0)
sum = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
674. 最长连续递增序列
【参考:674. 最长连续递增序列 - 力扣(LeetCode)】
【参考:代码随想录# 674. 最长连续递增序列】
dp[i]:以下标 i 为结尾的数组的连续递增的子序列长度为 dp[i]。
class Solution {
public static int findLengthOfLCIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp,1);
int res = 1;
for (int i = 0; i < nums.length - 1; i++) {
if (nums[i + 1] > nums[i]) {
dp[i + 1] = dp[i] + 1;
}
res=Math.max(res,dp[i + 1]);
}
return res;
}
}
贪心法
class Solution {
public int findLengthOfLCIS(int[] nums) {
int n=nums.length;
if(n==1) return 1;
int res=1;
int len=1;// 长度至少为1
for(int i=0;i<n-1;i++){
if(nums[i]<nums[i+1]){
len++;
res=Math.max(res,len);
}else{
len=1;
}
}
return res;
}
}
中等
322. 零钱兑换 ***
【参考:322. 零钱兑换 - 力扣(LeetCode)】
【参考:动态规划解题套路框架 :: labuladong 的算法小抄】
coins = [1, 2, 5], amount = 11
比如你想求 amount = 11 时的最少硬币数(原问题),如果你知道凑出 amount = 10 的最少硬币数(子问题),你只需要把子问题的答案加一(再选一枚面值为 1 的硬币)就是原问题的答案。因为硬币的数量是没有限制的,所以子问题之间没有相互制,是互相独立的。
要凑够 amount,就要选硬币,c1 至 ck 总要至少选一个,则选每种的最小个数是 1+dp[amount-ci],我们把每种硬币都选一遍,答案即为其中的最小值
F(11)=min { F(11-1),F(11-2),F(11-5) } + 1;
+1 是加上选择减去的那枚硬币
F(11-5) + 1 即等于把 F(11-5)的结果再加上选一枚面值为 5 的硬币的和
dp(n) 表示,输入一个目标金额 n,返回凑出目标金额 n 所需的最少硬币数量。
int coinChange(int[] coins, int amount) {
// 题目要求的最终结果是 dp(amount)
return dp(coins, amount)
}
int dp(int[] coins, int amount) {
// base case
if (amount == 0) return 0;
if (amount < 0) return -1;
int res = Integer.MAX_VALUE;
for (int coin : coins) { // 遍历硬币的面值
// 计算子问题的结果
int subProblem = dp(coins, amount - coin);
// 子问题无解则跳过
if (subProblem == -1) continue;
// 在子问题中选择最优解,然后加一(该面值为coin的硬币)
res = Math.min(res, subProblem + 1);
}
return res == Integer.MAX_VALUE ? -1 : res;
}
2、带备忘录的递归
int[] memo;
int coinChange(int[] coins, int amount) {
memo = new int[amount + 1];
// dp 数组全都初始化为特殊值
Arrays.fill(memo, -666);
return dp(coins, amount);
}
int dp(int[] coins, int amount) {
if (amount == 0) return 0;
if (amount < 0) return -1;
// 查备忘录,防止重复计算
if (memo[amount] != -666)
return memo[amount];
int res = Integer.MAX_VALUE;
for (int coin : coins) { // 遍历硬币的面值
// 计算子问题的结果
int subProblem = dp(coins, amount - coin);
// 子问题无解则跳过
if (subProblem == -1) continue;
// 在子问题中选择最优解,然后加一(该面值为coin的硬币)
res = Math.min(res, subProblem + 1);
}
// 把计算结果存入备忘录
memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
return memo[amount];
}
3、dp 数组的迭代解法
dp 数组的定义:当目标金额为 i 时,至少需要 dp[i] 枚硬币凑出。
int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
// 数组大小为 amount + 1,初始值也为 amount + 1
Arrays.fill(dp, amount + 1);
// base case
dp[0] = 0;
// 外层 for 循环在遍历所有状态的所有取值
for (int i = 0; i < dp.length; i++) {
// 内层 for 循环在求所有选择的最小值
for (int coin : coins) { // 遍历硬币的面值
// 子问题无解,跳过
if (i - coin < 0) {
continue;
}
// 加一(该面值为coin的硬币)
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}
// 等于初始值说明凑不到
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}
516. 最长回文子序列 ***
经典类型 第 1312 题
题解:https://leetcode-cn.com/problems/longest-palindromic-subsequence/solution/a-fei-xue-suan-fa-zhi-si-ke-yi-dao-ti-516-zui-chan/
方法 1:暴力递归
helper(String s, int start, int end) 函数表示,从start索引到end索引,所能找到的当前s的最长回文子序列的长度
base case:
start == end 当前单词只有一个字符,长度为1
start > end 不合法
public int longestPalindromeSubseq(String s) {
return helper(s, 0, s.length() - 1);
}
private int helper(String s, int start, int end) {
if (start == end) return 1;
if (start > end) return 0;
int result = 0;
if (s.charAt(start) == s.charAt(end)) {
result = helper(s, start + 1, end - 1) + 2;
} else {
result = Math.max(helper(s, start + 1, end),
helper(s, start, end - 1));
}
return result;
}
方法 2:带备忘录 memo 的递归
比暴力递归多了几行代码
自顶向下记忆化 DP(Top-down)
对方法 1 进行记忆化修改后可以得到方法 2
int[][] memo;
public int longestPalindromeSubseq(String s) {
memo = new int[s.length()][s.length()];
return helper(s, 0, s.length() - 1);
}
private int helper(String s, int start, int end) {
// 查询备忘录 避免重复计算
if(memo[start][end]!=0)
return memo[start][end];
// base case
if (start == end) return 1;
if (start > end) return 0;
int result = 0;
if (s.charAt(start) == s.charAt(end)) {
result = helper(s, start + 1, end - 1) + 2;
} else {
result = Math.max(helper(s, start + 1, end),
helper(s, start, end - 1));
}
memo[start][end] = result; // 记录下来
return result;
}
方法 3: 动态规划 dp
自底向上填表 DP(Bottom-up)
public int longestPalindromeSubseq1st(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for (int i = n - 1; i >= 0; i--) {
dp[i][i] = 1;
for (int j = i + 1; j < n; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
62. 不同路径 **
【参考:62. 不同路径 - 力扣(LeetCode)】
【参考:代码随想录# 62.不同路径】
- 暴力法(DFS)
可以转化为求二叉树叶子节点的个数
class Solution {
public int uniquePaths(int m, int n) {
return dfs(1, 1, m, n);// (1,1)->(m,n)
}
// (i,j)->(m,n)
public int dfs(int i, int j, int m, int n) {
if (i > m || j > n) // 越界了
return 0;
if (i == m && j == n) // 找到一种方法,相当于找到了叶子节点
return 1;
return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
}
}
- 动态规划
d p [ i ] [ j ] : 表 示 从 ( 0 , 0 ) 出 发 , 到 ( i , j ) 有 d p [ i ] [ j ] 条 不 同 的 路 径 。 dp[i][j] :表示从(0,0)出发,到(i, j) 有dp[i][j]条不同的路径。 dp[i][j]:表示从(0,0)出发,到(i,j)有dp[i][j]条不同的路径。
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
dp[i][0] = 1;// 最左面
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;// 最上面
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
63. 不同路径 II
【参考:63. 不同路径 II - 力扣(LeetCode)】
【参考:代码随想录# 63. 不同路径 II】
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m=obstacleGrid.length;
int n=obstacleGrid[0].length;
int[][] dp = new int[m][n];
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;// 最左面
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;// 最上面
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if(obstacleGrid[i][j] == 1)
continue;
// 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
343. 整数拆分(难)
【参考:343. 整数拆分 - 力扣(LeetCode)】
【参考:代码随想录# 343. 整数拆分】
待回顾
dp[i]:分拆数字 i,可以得到的最大乘积为 dp[i]。
class Solution {
public int integerBreak(int n) {
int[] dp=new int[n+1];
dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=1;j<i-1;j++){
dp[i]=Math.max(dp[i],Math.max((i-j)*j,dp[i-j]*j));
}
}
return dp[n];
}
}
96. 不同的二叉搜索树 hard
【参考:96. 不同的二叉搜索树 - 力扣(LeetCode)】
【参考:代码随想录# 96.不同的二叉搜索树】
494. 目标和 ??
【参考:494. 目标和 - 力扣(LeetCode)】
300. 最长递增子序列
【参考:300. 最长递增子序列 - 力扣(LeetCode)】
dp[i]表示 i 之前包括 i 的最长严格递增子序列的长度。
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
for (int i = 0; i < dp.length; i++) {
// dp[i]= nums[i] > nums[0..i-1] && dp[0..i-1]中最大的 +1
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) { // 保证严格递增
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}
718. 最长重复子数组
【参考:718. 最长重复子数组 - 力扣(LeetCode)】
【参考:「手画图解」动态规划 思路解析 | 718 最长重复子数组 - 最长重复子数组 - 力扣(LeetCode)】
dp[i][j] :长度为 i,末尾项为 A[i-1]的子数组,与长度为 j,末尾项为 B[j-1]的子数组,二者的最大公共后缀子数组长度。
如果 A[i-1] != B[j-1], 有 dp[i][j] = 0
如果 A[i-1] == B[j-1] , 有 dp[i][j] = dp[i-1][j-1] + 1
base case:如果 i=0 || j=0,则二者没有公共部分,dp[i][j]=0
最长公共子数组以哪一项为末尾项都有可能,求出每个 dp[i][j],找出最大值。
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int n=nums1.length,m=nums2.length;
int res=0;
int[][] dp=new int[n+1][m+1];
// base case
// dp[i][0]=dp[0][j]=0
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}
res=Math.max(res,dp[i][j]);
}
}
return res;
}
}
滑动窗口
【参考:lc 718. 最长重复子数组(三种解法:DP,滑动窗口,二分+哈希) - 最长重复子数组 - 力扣(LeetCode)】
// 滚动数组:时间复杂度: O( (N+M) × min(N,M) ),空间复杂度: O(1)
class Solution {
public:
int maxLength(vector<int>& A, vector<int>& B, int addA, int addB, int len) {
int ret = 0, k = 0;
for (int i = 0; i < len; i++) {
if (A[addA + i] == B[addB + i]) k++;
else k = 0;
ret = max(ret, k);
}
return ret;
}
int findLength(vector<int>& A, vector<int>& B) {
int n = A.size(), m = B.size();
int ret = 0;
for (int i = 0; i < n; i++) { // A不动, B[0] 与 A[i]对齐
int len = min(m, n - i);
// 每次对齐后可以计算一下长度len是否已经小于或等于结果ret
// 如果是,那我们就不用继续循环计算了,因为后面肯定没有更长的
if(len <= ret) break; // 加了这个提前结束条件,从击败84%到97%
int maxlen = maxLength(A, B, i, 0, len);
ret = max(ret, maxlen);
}
for (int i = 0; i < m; i++) { // B不动, A[0] 与 B[i]对齐
int len = min(n, m - i);
if(len <= ret) break; // 加了这个提前结束条件,从击败84%到97%
int maxlen = maxLength(A, B, 0, i, len);
ret = max(ret, maxlen);
}
return ret;
}
};
1143. 最长公共子序列 ***
【参考:1143. 最长公共子序列 - 力扣(LeetCode)】
【参考:代码随想录# 1143.最长公共子序列】
dp[i][j]:长度为[0, i - 1]的字符串 text1 与长度为[0, j - 1]的字符串 text2 的最长公共子序列为 dp[i][j]
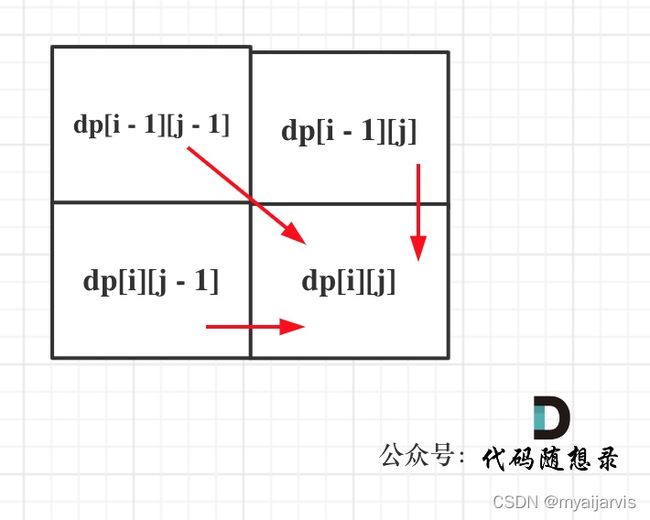
如果 text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以 dp[i][j] = dp[i - 1][j - 1] + 1;
如果 text1[i - 1] 与 text2[j - 1]不相同,那就看看
text1[0, i - 2]与 text2[0, j - 1]的最长公共子序列( d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j]) 和
text1[0, i - 1]与 text2[0, j - 2]的最长公共子序列( d p [ i ] [ j − 1 ] dp[i][j - 1] dp[i][j−1])
取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
【参考:最长公共子序列 | 图解 DP | 最清晰易懂的讲解 【c++/java 版本】 - 最长公共子序列 - 力扣(LeetCode)】
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int n=text1.length(),m=text2.length();
// dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
int[][] dp=new int[n+1][m+1];
// base case
// dp[i][0]=dp[0][j]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(text1.charAt(i-1)==text2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1]+1; // 延长一位
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]); // 无法延长,取之前的最大值
}
}
}
return dp[n][m];
}
}
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
n=len(text1)
m=len(text2)
dp=[ [0]*(m+1) for _ in range(n+1)] # 二维数组 这里要注意 里面是第二维,外面循环的是第一维
# base case
# dp[i][0]=dp[0][j]=0
for i in range(1,n+1):
for j in range(1,m+1):
if text1[i-1]==text2[j-1]:
dp[i][j]=dp[i-1][j-1]+1
else:
dp[i][j]=max(dp[i-1][j],dp[i][j-1])
return dp[n][m]
1035. 不相交的线
【参考:1035. 不相交的线 - 力扣(LeetCode)】
【参考:代码随想录# 1035.不相交的线】
直线不能相交,这就是说明在字符串 A 中 找到一个与字符串 B 相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
本题就和我们刚刚讲过的这道题目动态规划:1143.最长公共子序列就是一样一样的了。
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int n=nums1.length,m=nums2.length;
int[][] dp=new int[n+1][m+1];
// base case
// dp[i][0]=dp[0][j]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1; // 延长一位
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]); // 无法延长,取之前的最大值
}
}
}
return dp[n][m];
}
}
647. 回文子串 (***)
【参考:647. 回文子串 - 力扣(LeetCode)】
【参考:647. 回文子串 5. 最长回文子串 516. 最长回文子序列 三道回文相关题目汇总 - 回文子串 - 力扣(LeetCode)】
【参考:代码随想录# 647. 回文子串】从下到上,从左到右遍历
dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
情况一 j-i=0
情况二 j-i=1
if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1]))
class Solution {
public int countSubstrings(String s) {
int n=s.length();
boolean[][] dp = new boolean[n][n];
// base case
// dp[i][j]=false
int ans = 0;
// 注意遍历顺序
for (int i = n-1; i >=0; i--) {
for (int j = i; j < n; j++) {
if (s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1])) {
dp[i][j] = true;
ans++;
}
}
}
return ans;
}
}
动态规划看这个容易理解 【参考:两道回文子串的解法(详解中心扩展法) - 回文子串 - 力扣(LeetCode)】
图源【参考:「手画图解」动态规划 & 降维优化 | 647.回文子串 - 回文子串 - 力扣(LeetCode)】
从上到下,从左到右遍历

class Solution {
public int countSubstrings(String s) {
int n=s.length();
boolean[][] dp = new boolean[n][n];
// base case
// dp[i][j]=false
int ans = 0;
// 注意遍历顺序
for (int j = 0; j < n; j++) {
for (int i = 0; i <= j; i++) { // 上三角
if (s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1])) {
dp[i][j] = true;
ans++;
}
}
}
return ans;
}
}
【参考:「手画图解」动态规划 & 降维优化 | 647.回文子串 - 回文子串 - 力扣(LeetCode)】
class Solution {
public int countSubstrings(String s) {
int n=s.length();
boolean[][] dp = new boolean[n][n];
// base case
// dp[i][j]=false
int ans = 0;
// 注意遍历顺序
for (int j = 0; j < n; j++) {
for (int i = 0; i <= j; i++) {
if (i == j) { // 单个字符的情况
dp[i][j] = true;
ans++;
} else if (j - i == 1 && s.charAt(i) == s.charAt(j)) { // 两个字符的情况
dp[i][j] = true;
ans++;
// 多于两个字符
} else if (j - i > 1 && s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
dp[i][j] = true;
ans++;
}
}
}
return ans;
}
}
双指针法 ***
最优解
中心扩展法 【参考:两道回文子串的解法(详解中心扩展法) - 回文子串 - 力扣(LeetCode)】
代码【参考:代码随想录# 647. 回文子串】
首先确定回文串,就是找中心然后想两边扩散看是不是对称的就可以了。
在遍历中心点的时候,要注意中心点有两种情况。
一个元素可以作为中心点,两个元素也可以作为中心点。
那么有人同学问了,三个元素还可以做中心点呢。其实三个元素就可以由一个元素左右添加元素得到,四个元素则可以由两个元素左右添加元素得到。
所以我们在计算的时候,要注意一个元素为中心点和两个元素为中心点的情况。
class Solution {
public int countSubstrings(String s) {
int n=s.length();
int result=0;
for(int i=0;i<n;i++){
result+=extend(s,i,i,n);// 以i为中心
result+=extend(s,i,i+1,n);// 以i和i+1为中心
}
return result;
}
public static int extend(String s,int i,int j,int n){
int res=0; // s[i,j]中回文子串的数量
while(i>=0 && j<n && s.charAt(i)==s.charAt(j)){
res++;
// 从中心向两边扩散
i--;
j++;
}
return res;
}
}
516. 最长回文子序列(难)
【参考:516. 最长回文子序列 - 力扣(LeetCode)】
【参考:子序列解题模板:最长回文子序列_labuladong_微信公众号】 图文并茂
【参考:代码随想录# 516.最长回文子序列】
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
推荐这种反着遍历的遍历方式
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
// base case
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
// dp others is zero
for (int i = n - 1; i >= 0; i--) {
for (int j = i+1; j < n; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n-1];
}
}
斜着遍历
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
// base case
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
// dp others is zero
for (int j = 1; j < n; j++) {
for (int i = j-1; i >=0; i--) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n-1];
}
}
139. 单词拆分
【参考:139. 单词拆分 - 力扣(LeetCode)】
- 动态规划
【参考:「手画图解」剖析三种解法: DFS, BFS, 动态规划 |139.单词拆分 - 单词拆分 - 力扣(LeetCode)】
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> set=new HashSet<>(wordDict);
int len=s.length();
// s[0:i] 和python切片一样 左闭右开
// dp[i]:长度为i的s[0:i]子串是否能拆分成单词表中的单词。
// 题目求:dp[s.length]
boolean[] dp=new boolean[len+1];
dp[0]=true; // 默认空串可以
for(int i=1;i<=len;i++){
for(int j=0;j<i;j++){ // j把s[0:i]划分成两部分
// dp[j]=true s[0:j]
// s.substring(j,i) s[j:i]
if(dp[j] && set.contains(s.substring(j,i))){
dp[i]=true;// s[0:i]子串能拆分成单词表中的单词
break; // 没有必要继续划分了
}
}
}
return dp[len];
}
}
- labuladong
不加备忘录下面例子就会超时
"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
["a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa"]
class Solution {
// 备忘录
int[] memo;
public boolean wordBreak(String s, List<String> wordDict) {
// 备忘录,-1 代表未计算,0 代表 false,1 代表 true
memo = new int[s.length()];
Arrays.fill(memo, -1);
// 根据函数定义,判断 s[0..] 是否能够被拼出
return dp(s, 0, wordDict);
}
// 因为word的长度不一,所以相同的位置i可能会重复判断,需要备忘录记录一下
// 定义:返回 s[i..] 是否能够被 wordDict 拼出
boolean dp(String s, int i, List<String> wordDict) {
// base case,整个 s 都被拼出来了
if (i == s.length()) {
return true;
}
// 防止冗余计算
if (memo[i] != -1) {
return memo[i] == 1 ? true : false;
}
// 遍历所有单词,尝试匹配 s[i..] 的前缀
for (String word : wordDict) {
int len = word.length();
if (i + len > s.length()) {
continue;
}
String subStr = s.substring(i, i + len);
if (!subStr.equals(word)) {
continue; // 继续遍历下一个单词
}
// s[i..] 的前缀被word匹配,去尝试匹配 s[i+len..]
if (dp(s, i + len, wordDict)) {
memo[i] = 1; // s[i..] 可以被拼出,将结果记入备忘录
return true;
}
}
memo[i] = 0; // s[i..] 不能被拼出,结果记入备忘录
return false;
}
}
剑指 Offer II 091. 粉刷房子
【参考:剑指 Offer II 091. 粉刷房子 - 力扣(LeetCode)】
- 回溯法
class Solution {
int result=Integer.MAX_VALUE;
int n=0;
public int minCost(int[][] costs) {
n=costs.length;
ArrayList<Integer> list=new ArrayList<>();
dfs(costs,list,0,-1);
return result;
}
// index 当前房子下标
// pre 上一个房子的颜色
public void dfs(int[][] costs,List<Integer> list,int index,int pre){
if(index == n){
int sum=0;
for(int v:list){
sum+=v;
}
result=Math.min(result,sum);
return;
}
for(int i=0;i<3;i++){
if(i!=pre){ // 与上一个房子的颜色不同
list.add(costs[index][i]);
dfs(costs,list,index+1,i);
list.remove(list.size()-1); // 回溯
}
}
}
}
[[5,6,5],[15,8,8],[13,19,7],[16,1,9],[15,2,18],[13,18,8],[4,1,3],[3,3,3],[16,14,14],[7,6,1],[7,17,17],[8,20,10],[12,16,1],[8,11,8],[14,7,12],[8,18,13],[6,2,3],[16,1,11],[4,2,10],[17,16,17],[1,8,17],[1,12,17],[1,11,10]]
单独测试可以,提交就超时,不科学啊!
- 动态规划
【参考:粉刷房子 - 粉刷房子 - 力扣(LeetCode)】
class Solution {
public int minCost(int[][] costs) {
int n=costs.length;
//dp[i][j] 表示粉刷第0号房子到第i号房子且第i号房子被粉刷成第j种颜色时的最小花费成本
int[][] dp=new int[n][3];
// base case
dp[0][0]=costs[0][0];
dp[0][1]=costs[0][1];
dp[0][2]=costs[0][2];
for(int i=1;i<n;i++){
// 第i号房子选第0种颜色,那第i-1号房子就只能选其他两种颜色了
dp[i][0]=Math.min(dp[i-1][1],dp[i-1][2])+costs[i][0];
dp[i][1]=Math.min(dp[i-1][0],dp[i-1][2])+costs[i][1];
dp[i][2]=Math.min(dp[i-1][0],dp[i-1][1])+costs[i][2];
}
return Math.min(dp[n-1][0],
Math.min(dp[n-1][1],dp[n-1][2]));
}
}
873. 最长的斐波那契子序列的长度
【参考:873. 最长的斐波那契子序列的长度 - 力扣(LeetCode)】
【参考:最长的斐波那契子序列的长度【枚举+记忆化搜索+动态规划】 - 最长的斐波那契子序列的长度 - 力扣(LeetCode)】
class Solution {
Map<Integer,Integer> map=new HashMap<>();
int[][] memo;
public int lenLongestFibSubseq(int[] arr) {
int n=arr.length;
for(int i=0;i<n;i++){
map.put(arr[i],i);
}
int result=0;
memo=new int[n][n];
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
int count=dfs(i,j,arr);
if(count>=3){
result=Math.max(result,count);
}
}
}
return result;
}
// 记忆化搜索
public int dfs(int i,int j, int[] arr){
if(memo[i][j]>0) // 已经计算过了
return memo[i][j];
memo[i][j]=2; // 默认长度是两个 arr[i],arr[j]
// 查找下一个 arr[i],arr[j],key,.....
int key=arr[i]+arr[j];
if(map.containsKey(key)){
memo[i][j] = 1 + dfs(j,map.get(key),arr);
}
return memo[i][j];
}
}
困难
1312. 让字符串成为回文串的最少插入次数 ***
class Solution {
public int minInsertions(String s) {
return helper(s,0,s.length()-1);
}
public int helper(String s,int start,int end){
// base case
if(start>=end) return 0;
int result;
if(s.charAt(start)==s.charAt(end)){
result=helper(s,start+1,end-1); // 相等表示不需要插入
}else{
result=Math.min(helper(s,start+1,end),
helper(s,start,end-1)
)+1; // // 需要插入一次,取两边子串中总插入次数的最小值
}
return result;
}
}
方法 2:带备忘录 memo 的递归
class Solution {
int [][] memo;
public int minInsertions(String s) {
memo=new int[s.length()][s.length()];
return helper(s,0,s.length()-1);
}
public int helper(String s,int start,int end){
if(memo[start][end]!=0)
return memo[start][end];
// base case
if(start>=end) return 0;
int result;
if(s.charAt(start)==s.charAt(end)){
result=helper(s,start+1,end-1); // 相等表示不需要插入
}else{
result=Math.min(helper(s,start+1,end),
helper(s,start,end-1)
)+1; // // 需要插入一次,取两边子串中总插入次数的最小值
}
memo[start][end]=result;
return result;
}
}
class Solution {
public int minInsertions(String s) {
int n=s.length();
int[][] dp=new int[n][n];
for(int i=n-1;i>=0;i--){
dp[i][i]=0;
for(int j=i+1;j<n;j++){
if(s.charAt(i)==s.charAt(j)){
dp[i][j]=dp[i+1][j-1]; // 相等表示不需要插入
}else{
// 需要插入一次,取两边子串中总插入次数的最小值
dp[i][j]=Math.min(dp[i+1][j],dp[i][j-1])+1;
}
}
}
return dp[0][n-1];
}
}