高阶数据结构学习 —— 图(3)
文章目录
- 1、最小生成树概念
- 2、Kruskal算法
- 3、Prim算法
1、最小生成树概念
先看一下连通图和生成树的概念
连通图。在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。注意这是无向图中的概念
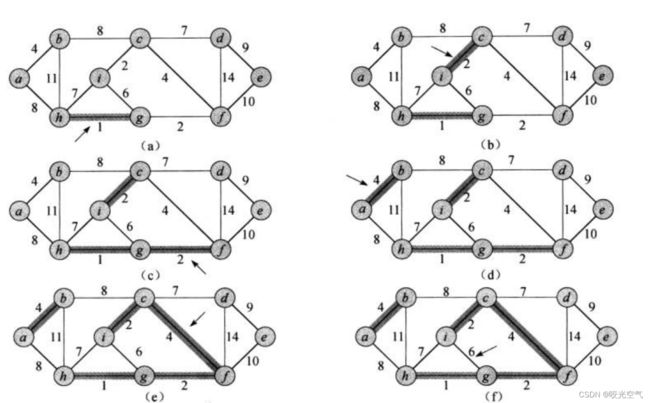
这一篇来解决最小生成树问题。生成树是通过最少边连通起来所有顶点,其实就是n - 1个边,因为有n个顶点。最小则指所有边的权值和最小。并且这些边不能构成回路。下图就是回路。

最小生成树通过贪心来设计,有两个算法Kruskal(克鲁斯卡尔)和Prim(普里姆)算法。
2、Kruskal算法
每次都选所有边中最小的边,这个可以事先排序一下,更好的办法是优先级队列。至于权值相等的,就是选择其中一个,再去选另一个。但这里因为有不能构成回路问题,无论选哪个边,都需要先判断能否选择。回路的判断就是假设要连ab两点,但在此之前,b已经能通过别的多个边连接到a了,那么此时就不能连接,一连就回路了。所以我们要去走一遍路径看能不能成?这很低效,这里优雅的做法就是用并查集,连接的两点放到一个集合中,这样像上图i和g,当cf连接起来后,ci所在的集合就与gf所在的集合合并起来了,这时候gi就在一个集合中,那么选到gi边时发现在一个集合就不选它了。
最小生成树就是子图,它用到的信息和主图一样。把这个算法函数放在邻接矩阵的Graph类里。
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
typedef Graph<V, W, MAX_W, Direction> Self;
public:
权值在_matrix这里,这样使用不方便,单独给这个算法造一个边的结构体。
void _AddEdge(size_t srci, size_t dsti, const W& w)//重载,为了Kruskal算法
{
_matrix[srci][dsti] = w;
if (Direction == false)
_matrix[dsti][srci] = w;
}
void AddEdge(const V& src, const V& dst, const W& w)//增加边的话,应当传源点,目标点,权值
{
//即使抛异常程序还能执行,但程序员已经知道程序错误了,最后程序正常地异常结束
//assert则是暴力退出,且只在debug模式下才有assert,release模式下就屏蔽assert了
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
//有向图和无向图区分
_AddEdge(srci, dsti, w);
}
//......
struct Edge
{
size_t _srci;
size_t _dsti;
const W _w;
Edge(size_t srci, size_t dsti, const W& w)
:_srci(srci)
, _dsti(dsti)
, _w(w)
{}
bool operator>(const Edge& e) const
{
return _w > e._w;
}
};
W Kruskal(Self& minTree)
{
priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
size_t n = _vertexs.size();//矩阵大小一定是n阶方阵,也就是n * n
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (i < j && _matrix[i][j] != MAX_W)//为了防止无向图的重复添加,就规定i < j,这样[j][i]就不会插入了
{
minque.push(Edge(i, j, _matrix[i][j]));
}
}
}
//选出n - 1条边
UnionFindSet ufs(n);
while (!minque.empty())
{
Edge min = minque.top();
minque.pop();
if (!ufs.InSameSet(min._srci, min._dsti))
{
//通过上面的代码知道,srci和dsti都是顶点的下标,而原AddEdge函数接收的是顶点,所以我们写一个_AddEdge,原函数还可以复用它
minTree._AddEdge(min._srci, min._dsti, min._w);//不用函数重载的原因是防止V被初始化成size_t类型的
ufs.Union(min._srci, min._dsti);
}
}
}
现在再添加上权值的记录以及判断。
//选出n - 1条边
int sz = 0;
W totalW = W();
UnionFindSet ufs(n);
while (!minque.empty())
{
Edge min = minque.top();
minque.pop();
if (!ufs.InSet(min._srci, min._dsti))
{
//通过上面的代码知道,srci和dsti都是顶点的下标,而原AddEdge函数接收的是顶点,所以我们写一个_AddEdge,原函数还可以复用它
minTree._AddEdge(min._srci, min._dsti, min._w);//不用函数重载的原因是防止V被初始化成size_t类型的
ufs.Union(min._srci, min._dsti);
++sz;
totalW += min._w;
}
else
{
cout << "构成回路: " << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
}
}
if (sz == n - 1) return totalW;
else return W();
如果size是n - 1那就说明能得到最小生成树,然后返回权值和,不能就返回一个缺省值,0。
测试代码。不过类里写上Graph() = default。因为下面的测试是用的无参构造,我们使用默认的就行。
void TestGraphMinTree()
{
const char str[] = "abcdefghi";
Graph<char, int> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
Graph<char, int> kminTree;
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.Print();
}
如果这样运行,就会崩掉。原因是传进来的kminTree需要初始化,因为这是默认构造出来的。
//先初始化成可用的
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
priority_queue<Edge, vector<Edge>, greater<Edge>> minque;//#include 3、Prim算法
这个算法在全局选最小。选定一个起点,找连接这个点的最小权值的边,假设选到a连接b的边,那就下一步从b开始找连接b的最小权值的边。
Prim的思路就是用两个集合,一个是选中的点,一个是没选中的点,所以它不需要并查集。
W Prim(Self& minTree, const W& src)
{
//初始化
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
set<int> X;
set<int> Y;
X.insert(srci);
for (size_t i = 0; i < n; ++i)
{
if (i != srci) Y.insert(i);
}
}
接下来怎么选边?如果用优先级队列,把每一个点连接的边的权值都放进来,这并不可取,因为优先级队列删除的是堆顶,而有的边并不是堆顶,比如上图,到最后时,不能选择ah,但按照优先级队列,有可能就选择上了,这时候a和h应当都在X集合里,所以这个思路是错误的。如果直接遍历选边,其实也不行,效率不高,也有可能出现回路。
这里的思路还是用优先级队列,但做些别的操作,每次添加边时判断是否构成回路,环,判断的方法就是两个点都在一个集合里就会构成回路,不构成的再放进集合里。
W Prim(Self& minTree, const W& src)
{
//初始化
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
set<int> X;
set<int> Y;
X.insert(srci);
for (size_t i = 0; i < n; ++i)
{
if (i != srci) Y.insert(i);
}
priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
//先把srci连接的边添加到队列中,起点处不需要判断
for (size_t i = 0; i < n; ++i)
{
if (_matrix[srci][i] != MAX_W)
{
minq.push(Edge(srci, i, _matrix[srci][i]));
}
}
cout << "Prim开始选边" << endl;
size_t sz = 0;
W totalW = W();
while (!minq.empty())
{
Edge min = minq.top();
minq.pop();
minTree._AddEdge(min._srci, min._dsti, min._w);
X.insert(min._dsti);
Y.erase(min._dsti);
++sz;
totalW += min._w;
if (sz == n - 1) break;
for (size_t i = 0; i < n; ++i)
{
if (_matrix[min._dsti][i] != MAX_W && X.count(i) == 0)//i必须不在X里,用计数的函数,为0就说明不在
{
minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
}
}
}
return totalW;
}
测试代码
void Print()
{
// 顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
// 矩阵
// 横下标
cout << " ";
for (size_t i = 0; i < _vertexs.size(); ++i)
{
printf("%4d", i);
}
cout << endl;
for (size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " "; // 竖下标
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (_matrix[i][j] == MAX_W)
{
printf("%4c", '*');
}
else
{
printf("%4d", _matrix[i][j]);
}
}
cout << endl;
}
cout << endl;
for (size_t i = 0; i < _matrix.size(); ++i)
{
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (i < j && _matrix[i][j] != MAX_W)
{
cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;
}
}
}
}
void TestGraphMinTree()
{
const char str[] = "abcdefghi";
Graph<char, int> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('c', 'd', 7);
g.AddEdge('d', 'f', 14);
g.AddEdge('d', 'e', 9);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
Graph<char, int> kminTree;
cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
kminTree.Print();
cout << endl << endl;
Graph<char, int> pminTree;
cout << "Prim:" << g.Prim(pminTree, 'a') << endl;
pminTree.Print();
cout << endl;
}
但是按照上面的代码,会构成回路,g和i那里是回路。修改一下
W Prim(Self& minTree, const W& src)
{
//初始化
size_t srci = GetVertexIndex(src);
size_t n = _vertexs.size();
minTree._vertexs = _vertexs;
minTree._indexMap = _indexMap;
minTree._matrix.resize(n);
for (size_t i = 0; i < n; ++i)
{
minTree._matrix[i].resize(n, MAX_W);
}
vector<bool> X(n, false);
vector<bool> Y(n, true);
X[srci] = true;
Y[srci] = false;
priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
//先把srci连接的边添加到队列中,起点处不需要判断
for (size_t i = 0; i < n; ++i)
{
if (_matrix[srci][i] != MAX_W)
{
minq.push(Edge(srci, i, _matrix[srci][i]));
}
}
cout << "Prim开始选边" << endl;
size_t sz = 0;
W totalW = W();
while (!minq.empty())
{
Edge min = minq.top();
minq.pop();
if (X[min._dsti])//起点一定在集合,只要目标点也在就构成环
{
cout << "构成环:";
cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
}
else
{
minTree._AddEdge(min._srci, min._dsti, min._w);
X[min._dsti] = true;
Y[min._dsti] = false;
++sz;
totalW += min._w;
if (sz == n - 1) break;
for (size_t i = 0; i < n; ++i)
{
if (_matrix[min._dsti][i] != MAX_W && Y[i])//i必须在Y集合才能插入
{
minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
}
}
}
}
if (sz == n - 1) return totalW;
else return W();
}
K算法是固定的树,P算法起点不同,选出来的树一样,在测试代码最后加上这个来观察。
for (size_t i = 0; i < strlen(str); ++i)
{
cout << "Prim:" << g.Prim(pminTree, str[i]) << endl;
}
本篇gitee
下一篇写最短路径问题。
结束。