【JAVA数据结构系列】07_Set&Map详解
文章目录
- 1. 搜索
-
- 1.1 概念及场景
- 1.2 模型
- 2. Map 的使用
-
- 2.1 关于Map的说明
- 2.2 关于Map.Entry
1. 搜索
1.1 概念及场景
Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。以前常见的搜索方式有:
- 直接遍历,时间复杂度为O(N),元素如果比较多效率会非常慢。
- 二分查找,时间复杂度为 O(log2N) ,但搜索前必须要求序列是有序的。
上述排序比较适合静态类型的查找,即一般不会对区间进行插入和删除操作了,而现实中的查找比如:
- 根据姓名查询考试成绩。
- 通讯录,即根据姓名查询联系方式。
- 不重复集合,即需要先搜索关键字是否已经在集合中。
可能在查找时进行一些插入和删除的操作,即动态查找,那上述两种方式就不太适合了,本节介绍的Map和Set是 一种适合动态查找的集合容器。
1.2 模型
一般把搜索的数据称为关键字(Key),和关键字对应的称为值(Value),将其称之为Key-value的键值对(即python当中的字典),所以模型会有两种:
- 纯 key 模型,比如:
有一个英文词典,快速查找一个单词是否在词典中
快速查找某个名字在不在通讯录中 - Key-Value 模型,比如:
统计文件中每个单词出现的次数,统计结果是每个单词都有与其对应的次数: <单词,单词出现的次数> 梁山好汉的江湖绰号:每个好汉都有自己的江湖绰号
而Map中存储的就是key-value的键值对, Set中只存储了Key。
2. Map 的使用
2.1 关于Map的说明
Map是一个接口类,该类没有继承自Collection,该类中存储的是
Map<String,Integer> map=new TreeMap<>();//底层红黑树
Map<String,Integer> map2=new HashMap<>();//底层哈希表
2.2 关于Map.Entry的说明
Map.Entry
| 方法 | 解释 |
|---|---|
| K getKey() | 返回 entry 中的 key |
| V getValue() | 返回 entry 中的 value |
| V setValue(V value) | 将键值对中的value替换为指定value |
注意: Map.Entry
2.3 Map 的常用方法说明
| 方法 | 解释 |
|---|---|
| V get(Object key) | 返回 key 对应的value |
| V getOrDefault(Object key, V defaultValue) | 返回 key 对应的value , key 不存在,返回默认值 |
| V put(K key, V value) | 设置 key 对应的value |
| V remove(Object key) | 删除 key 对应的映射关系 |
| Set keySet() | 返回所有 key 的不重复集合 |
| Collection values() | 返回所有 value 的可重复集合 |
| Set |
返回所有的 key-value 映射关系 |
| boolean containsKey(Object key) | 判断是否包含 key |
| boolean containsValue(Object value) | 判断是否包含 value |
注意:
- Map是一个接口,不能直接实例化对象,如果要实例化对象只能实例化其实现类TreeMap或者HashMap
- Map中存放键值对的Key是唯一的, value是可以重复的
- Map中的Key可以全部分离出来,存储到Set中来进行访问(因为Key不能重复)。
- Map中的value可以全部分离出来,存储在Collection的任何一个子集合中(value可能有重复)。
- Map中键值对的Key不能直接修改, value可以修改,如果要修改key,只能先将该key删除掉,然后再来进行 重新插入。
2.3.1 TreeMap的put方法
Map<String,Integer> map=new TreeMap<>();//底层红黑树
map.put("can",10);
map.put("apple",3);
map.put("fish",8);
System.out.println(map);
进一步思考:如果key的插入是要比较大小的,则说明key本身是具有可比较的功能的。
解决方法:实现Comparable接口
class Student implements Comparable<Student>{
@Override
public int compareTo(Student o) {
return 0;
}
}
public class Test01 {
public static void main(String[] args) {
Map<Student,Integer> map2=new TreeMap<>();
map2.put(new Student(),1);
}
}
注意:
- 1、对于put方法,尤其要注意自定义类型必须要可比较。
- 2、put里面不能放null,否则报错。
- 3、如果两个put方法的key值相同,前面的value值会被后面的替换。(下面代码的最终结果fish等于10)
map.put("fish",8);
map.put("fish",10);
2.3.2 get方法
- 1、get可以获取key对应的值
Map<String,Integer> map=new TreeMap<>();//底层红黑树
map.put("can",10);
System.out.println(map.get("can"));//得到 10
- 2、如果没有对应的key,则使用get方法会返回null值。
- 3、
map.getOrDefault方法:如果没有key,则返回赋的默认值
System.out.println(map.getOrDefault("can",100));
2.3.3 keySet方法
- 将map当中所有的key都放到set集合当中。
- 返回所有 key 的不重复集合
Map<String,Integer> map=new TreeMap<>();//底层红黑树
map.put("can",10);
map.put("apple",3);
map.put("fish",8);
map.put("fish",10);
Set<String> set=map.keySet();
System.out.println(set); //[apple, can, fish]
2.3.4 values方法
- 将map当中所有的values都放到list集合当中。
- 返回所有 values的可重复集合
Map<String,Integer> map=new TreeMap<>();//底层红黑树
map.put("can",10);
map.put("apple",3);
map.put("fish",8);
map.put("fish",10);
Collection<Integer> list=map.values();
System.out.println(list); //[3, 10, 10]
2.3.5 entrySet方法
HashMap这个方法的entrySet()方法,这个方法返回返回的是一个Set对象,很多人以为返回的是一个包含了Map里面所有键值对的一个集合对象,这个理解不准确,通过这个Set对象,我们确实可以获取到Map里面存放的所有键值对,但是这个集合对象本身是不存放数据的,它只是助于我们遍历Map中的数据,类似于Iterator。下面我们来看看源码简要分析一下。
- entry是放在map接口里面的接口
- 实现map类的接口也一定要实现entry接口
map.put("can",10);
map.put("apple",3);
map.put("fish",8);
Set<Map.Entry<String,Integer>> entrySet=map.entrySet();
for(Map.Entry<String,Integer> entry:entrySet){
System.out.println("key:"+entry.getKey()+",val:"+entry.getValue());
}
2.5.6 HashMap的put方法
2.5.6. TreeMap和HashMap的区别
| Map底层结构 | TreeMap | HashMap |
|---|---|---|
| 底层结构 | 红黑树 | 哈希桶 |
| 插入/删除/查找时间复杂度 | O(log2N) | O(1) |
| 是否有序 | 关于Key有序 | 无序 |
| 线程安全 | 不安全 | 不安全 |
| 插入/删除/查找区别 | 需要进行元素比较 | 通过哈希函数计算哈希地址 |
| 比较与覆写 | key必须能够比较,否则会抛出ClassCastException异常 | 自定义类型需要覆写equals和 hashCode方法 |
| 应用场景 | 需要Key有序场景下 | Key是否有序不关心,需要更高的时间性能 |
3. Set 的说明
Set与Map主要的不同有两点: Set是继承自Collection的接口类, Set中只存储了Key。
3.1 set常见方法说明
| 方法 | 解释 |
|---|---|
| boolean add(E e) | 添加元素,但重复元素不会被添加成功 |
| void clear() | 清空集合 |
| boolean contains(Object o) | 判断 o 是否在集合中 |
| Iterator iterator() | 返回迭代器 |
| boolean remove(Object o) | 删除集合中的 o |
| int size() | 返回set中元素的个数 |
| boolean isEmpty() | 检测set是否为空,空返回true,否则返回false |
| Object[] toArray() | 将set中的元素转换为数组返回 |
| boolean containsAll(Collection c) | 集合c中的元素是否在set中全部存在,是返回true,否则返回 false |
| boolean addAll(Collection c) | 将集合c中的元素添加到set中,可以达到去重的效果 |
- Set是继承自Collection的一个接口类
- Set中只存储了key,并且要求key一定要唯一
- Set的底层是使用Map来实现的,其使用key与Object的一个默认对象作为键值对插入到Map中的
- Set最大的功能就是对集合中的元素进行去重
- 实现Set接口的常用类有TreeSet和HashSet,还有一个LinkedHashSet ,LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。
- Set中的Key不能修改,如果要修改,先将原来的删除掉,然后再重新插入
- TreeSet中不能插入null的key,HashSet可以。
3.2 TreeSet和HashSet的区别
| Set底层结构 | TreeSet | HashSet |
|---|---|---|
| 底层结构 | 红黑树 | 哈希桶 |
| 插入/删除/查找时间 复杂度 | O(log2N) | O(1) |
| 是否有序 | 关于Key有序 | 不一定有序 |
| 线程安全 | 不安全 | 不安全 |
| 插入/删除/查找区别 | 按照红黑树的特性来进行插入和删除 | 1. 先计算key哈希地址 2. 然后进行 插入和删除 |
| 比较与覆写 | key必须能够比较,否则会抛出ClassCastException异常 | 自定义类型需要覆写equals和hashCode方法 |
| 应用场景 | 需要Key有序场景下 | Key是否有序不关心,需要更高的时间性能 |
3.2.1 HashSet的add方法
由此就知道了为什么set当中的元素不能重复:因为TreeSet存储的元素是key,而key不能重复!
4. 题目
1、10W个数据,把这10W个数据当中的重复元素删除掉。
直接存储到Set当中。
public static void func1(int[] array){
Set<Integer> set=new HashSet<>();
//这里不使用TreeSet因为HashSet效率更高O(1)
for(int i=0;i< array.length;i++){
set.add(array[i]);
}
}
2、10W个数据,找到这10W个数据当中第一个重复的数据。
往集合存储的时候,发现集合已经存在了,就是重复的。
public static int func2(int[] array){
Set<Integer> set=new HashSet<>();
for(int i=0;i< array.length;i++){
if(!set.contains(array[i])){
set.add(array[i]);
}else{
return array[i];
}
}
return -1;
}
3、10W个数据,统计这10W个数据当中,每个数据出现的次数。
public static void func3(int[] array){
//key:关键字 val:次数
Map<Integer,Integer> map=new HashMap<>();
for(int i=0;i< array.length;i++){
int key=array[i];
if (map.get(key)==null) {
map.put(key,1);
}else{
int val=map.get(key);
map.put(key,val+1);
}
}
System.out.println(map);
}
public class Test03 {
//1、10W个数据,把这10W个数据当中的重复元素删除掉。
public static void func1(int[] array){
Set<Integer> set=new HashSet<>();
//这里不使用TreeSet因为HashSet效率更高O(1)
for(int i=0;i< array.length;i++){
set.add(array[i]);
}
}
//2、10W个数据,找到这10W个数据当中第一个重复的数据。
public static int func2(int[] array){
Set<Integer> set=new HashSet<>();
for(int i=0;i< array.length;i++){
if(!set.contains(array[i])){
set.add(array[i]);
}else{
return array[i];
}
}
return -1;
}
//3、10W个数据,统计这10W个数据当中,每个数据出现的次数。
public static void func3(int[] array){
//key:关键字 val:次数
Map<Integer,Integer> map=new HashMap<>();
for(int i=0;i< array.length;i++){
int key=array[i];
if (map.get(key)==null) {
map.put(key,1);
}else{
int val=map.get(key);
map.put(key,val+1);
}
}
System.out.println(map);
}
public static void main(String[] args) {
int[] array=new int[10_0000];
Random random=new Random();
for(int i=0;i< array.length;i++){
array[i]=random.nextInt(5_000);
}
func1(array);
System.out.println(func2(array));
func3(array);
}
}
4.1 只出现一次
题目》》》》》》》》》》》》》
方法一:异或运算
异或(xor)是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”,计算机符号为“xor”。
二进制下异或运算法则:
1 xor 1=0
0 xor 0=0
1 xor 0=1
0 xor 1=1
因此十进制下相同数字异或结果为0,数字a与0异或结果仍为原来的数字a。
另外有:
a ⊕ a = 0
a ⊕ b = b ⊕ a
a ⊕ b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c;
a ⊕ b ⊕ a = b.
因此本题中异或全部的元素的结果就是那个只出现1次的元素。
class Solution {
public int singleNumber(int[] nums) {
int ret=0;
for(int i=0;i<nums.length;i++){
ret^=nums[i];
}
return ret;
}
}
最开始异或0的原因是0和任何数进行异或的结果都是其本身。
方法二:异或运算
思想:使用set来做,当set当中没有此元素时,就放入set当中,当已经有此元素时,就从set当中删除此元素,最后遍历完成时set里面的元素就是只有一次的元素。
class Solution {
public int singleNumber(int[] nums) {
Set<Integer> set=new HashSet<>();
for(int i=0;i<nums.length;i++){
if(set.contains(nums[i])){
set.remove(nums[i]);
}else{
set.add(nums[i]);
}
}
for(int i=0;i<nums.length;i++){
if(set.contains(nums[i])){
return nums[i];
}
}
return -1;
}
}
时间复杂度:O(N)
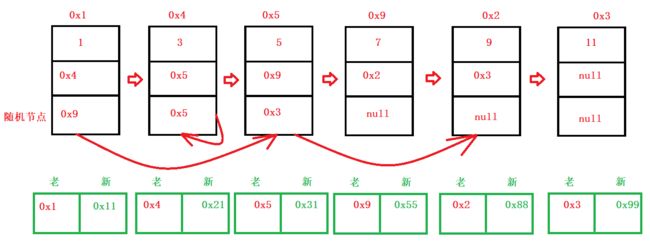
4.2 复制带随机指针的链表
题目》》》》》》》》》》》》
- 1、记录新老节点的对应关系
- 2、再次遍历链表,修改对应关系
- 因此需要遍历两遍列表
class Solution {
public Node copyRandomList(Node head) {
//这里不可以使用TreeMap,因为如果使用TreeMap就必须给Node实现一个可比较的接口
Map<Node,Node> map=new HashMap<>();
//1、第一次遍历链表
Node cur=head;
while(cur!=null){
Node node=new Node(cur.val);
map.put(cur,node);
cur=cur.next;
}
//2、第二次遍历链表
cur=head;
while(cur!=null){
map.get(cur).next=map.get(cur.next);
map.get(cur).random=map.get(cur.random);
cur=cur.next;
}
//3、最后返回头结点
return map.get(head);
}
}
4.3 宝石与石头
题目》》》》》》
方法一:将石头放到Map集合当中
class Solution {
public int numJewelsInStones(String jewels, String stones) {
Map<Character,Integer> map=new HashMap<>();
int ret=0;
for(int i=0;i<stones.length();i++){
if(map.containsKey(stones.charAt(i))){
int val=map.get(stones.charAt(i));
map.put(stones.charAt(i),val+1);
}else{
map.put(stones.charAt(i),1);
}
}
for(int i=0;i<jewels.length();i++){
if(map.containsKey(jewels.charAt(i))){
ret+=map.get(jewels.charAt(i));
}
}
return ret;
}
}
class Solution {
public int numJewelsInStones(String jewels, String stones) {
Set<Character> set=new HashSet<>();
//把宝石存储在集合当中
//toCharArray()方法,就是将字符串对象中的字符转换为一个字符数组。
for(char ch:jewels.toCharArray()){
set.add(ch);
}
int count=0;//宝石计数器
//遍历石头,查看石头当中有多少宝石
for(char ch:stones.toCharArray()){
if(set.contains(ch)){
count++;
}
}
return count;
}
}
4.4 旧键盘
题目》》》》》》》》》
- 1、由于输出的要大写,因此要把期望输入的字符都转换为大写,然后存入set集合。
- 2、解决输出的可能有重复的问题:将坏键重新装入一个新的集合set2。
import java.util.*;
public class Main{
public static void func(String s1,String s2){
Set<Character> set=new HashSet<>();
Set<Character> set2=new HashSet<>();
//将s2实际输入的字符串转变为大写,然后放到集合当中
for(char ch:s2.toUpperCase().toCharArray()){
set.add(ch);
}
//遍历期望输入的字符串,转变为大写,和集合当中比较
for(char ch:s1.toUpperCase().toCharArray()){
if(!set.contains(ch) && !set2.contains(ch)){
System.out.print(ch);
set2.add(ch);
}
}
}
public static void main(String[] args){
Set<Character> set=new HashSet<>();
Scanner scan=new Scanner(System.in);
while(scan.hasNextLine()){
String s1=scan.nextLine();//期望输入的
String s2=scan.nextLine();//实际输入的
func(s1,s2);
}
}
}
4.5 前K个高频单词
题目》》》》》》》》》》》》》
- 1、要求前K个次数最多的单词,因此建立小根堆
- 2、当频率相同时,按照字典顺序输出,因此在频率相同时,比较器里面要放大根堆。
步骤:
1、统计单词出现的次数
2、建立大小为k的小根堆
3、遍历map,先放满k个,然后从k+1开始,和堆顶元素比较
- 3.1 如果小根堆没有被放满k个,则直接放进去
- 3.2 如果已经放满了小根堆,则需要让当前元素和堆顶元素比较
- 3.3 此时考虑频率相同,key小的入队
class Solution {
public static List<String> topKFrequent(String[] words, int k) {
Map<String,Integer> map=new HashMap<>();
//1、统计单词出现的次数
for(String s:words){
if(map.get(s)==null){
map.put(s,1);
}else{
int val=map.get(s);
map.put(s,val+1);
}
}
//2、建立大小为k的小根堆
PriorityQueue<Map.Entry<String,Integer>> minQ=
new PriorityQueue<>(k,new Comparator<Map.Entry<String,Integer>>() {
@Override
public int compare(Map.Entry<String,Integer> o1,Map.Entry<String,Integer> o2){
//频率相同的时候,把这个变成以key为准的大根堆
if(o1.getValue().compareTo(o2.getValue())==0){
return o2.getKey().compareTo(o1.getKey());
}
return o1.getValue().compareTo(o2.getValue());//根据单词出现的频率创建小根堆
}
});
//3、遍历map,先放满k个,然后从k+1开始,和堆顶元素比较
for(Map.Entry<String,Integer> entry:map.entrySet()){
//3.1 如果小根堆没有被放满k个,则直接放进去
if(minQ.size()<k){
minQ.offer(entry);
}else {
Map.Entry<String, Integer> top = minQ.peek();
if(top!=null){
//3.2 如果已经放满了小根堆,则需要让当前元素和堆顶元素比较
if (entry.getValue() > top.getValue()) {
minQ.poll();
minQ.offer(entry);
} else {
//3.3 此时考虑频率相同,key小的入队
if (top.getValue().compareTo(entry.getValue()) == 0) {
if (top.getKey().compareTo(entry.getKey()) > 0) {
minQ.poll();
minQ.offer(entry);
}
}
}
}
}
}
List<String> ret=new ArrayList<>();
for(int i=0;i<k;i++){
Map.Entry<String,Integer> top=minQ.poll();
if(top!=null){
ret.add(top.getKey());
}
}
Collections.reverse(ret);
return ret;
}
}
5. 二叉搜索树
5.1 概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
int a [] ={5,3,4,1,7,8,2,6,0,9};
5.2 操作-查找
5.3 操作-插入
- 插入的节点都在叶子节点的地方。
- 插入相同的数据,则不能插入成功。
- 使用parent来记住cur的父节点。记住parent的原因在于最终决定要插入的节点是成为parent的左子节点还是右子节点。
- 如果树为空树,即根 == null,直接插入
- 如果树不是空树,按照查找逻辑确定插入位置,插入新结点
/**
* 插入节点
* @param key
*/
public boolean insert(int key){
TreeNode node=new TreeNode(key);
if(root==null){
root=node;
return true;
}
TreeNode cur=root;
TreeNode parent=null;
while(cur!=null){
if(cur.val<key){
parent=cur;
cur=cur.right;
}else if(cur.val>key){
parent=cur;
cur=cur.left;
}else{
return false;
//存在相同的元素,不能插入成功
}
}
if(parent.val<key){
parent.right=node;
}else{
parent.left=node;
}
return false;
}
public class Test {
public static void main(String[] args) {
BinarySearchTree binarySearchTree=new BinarySearchTree();
int[] array={80,30,48,56,60,90};
for(int i=0;i<array.length;i++){
binarySearchTree.insert(array[i]);
}
System.out.println("====");//此处设置断点
}
}
5.4 操作-删除
- 1、找到需要删除的节点cur
- 2、记住要删除节点的父亲节点parent
设待删除结点为 cur, 待删除结点的双亲结点为 parent:
- cur.left == null (左子树为空)
- cur 是 root,则 root = cur.right
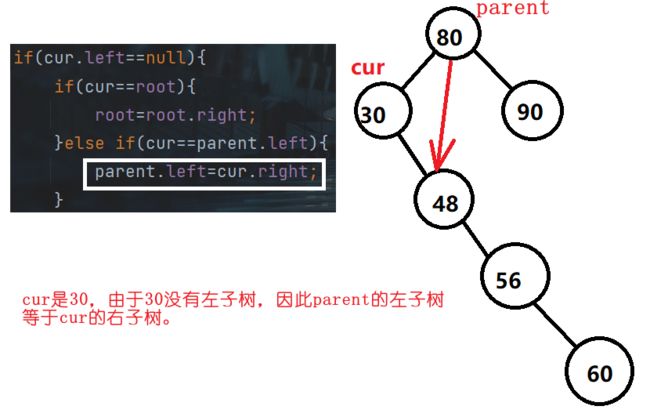
- cur 不是 root ,cur 是 parent.left,则 parent.left = cur.right
- cur 不是 root ,cur 是 parent.right,则 parent.right = cur.right
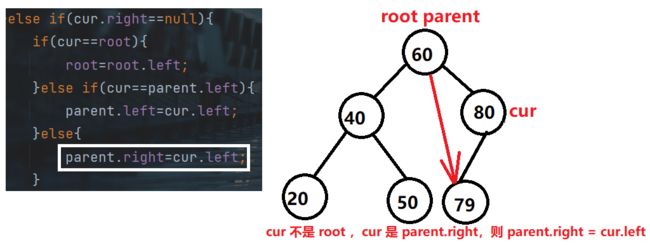
- cur.right == null (右子树为空)
- cur 是 root,则 root = cur.left
- cur 不是 root ,cur 是 parent.left,则 parent.left = cur.left
- cur 不是 root ,cur 是 parent.right,则 parent.right = cur.left
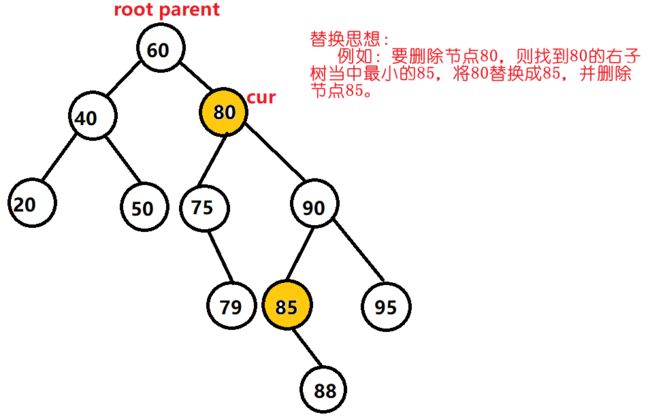
- cur.left != null && cur.right != null (左右子树都不为空)
- 需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被 删除节点中,再来处理该结点的删除问题
1、左子树为空的情况下:
2、右子树为空的情况下:
/**
* 删除关键字为key的节点
* @param key
*/
public void remove(int key){
TreeNode cur=root;
TreeNode parent=null;
while(cur!=null){
if(cur.val<key){
parent=cur;
cur=cur.right;
}else if(cur.val>key){
parent=cur;
cur=cur.left;
}else{
//找到了,开始删除
remove(cur,parent);
return;//删完之后要return,否则死循环
}
}
}
/**
* 删除节点
* @param cur 删除的节点
* @param parent 删除节点的父节点
*/
private void remove(TreeNode cur, TreeNode parent) {
if(cur.left==null){
if(cur==root){
root=root.right;
}else if(cur==parent.left){
parent.left=cur.right;
}else{
parent.right=cur.right;
}
}else if(cur.right==null){
if(cur==root){
root=root.left;
}else if(cur==parent.left){
parent.left=cur.left;
}else{
parent.right=cur.left;
}
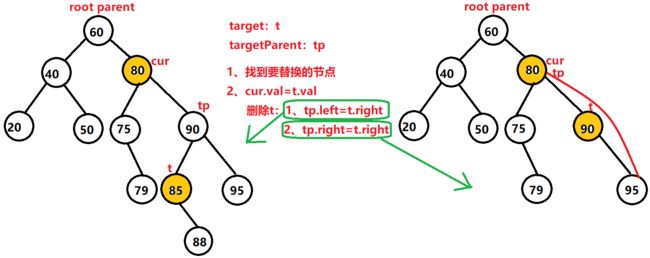
}else{
TreeNode targetParent=cur;
TreeNode target=cur.right;
while(target.left!=null){
targetParent=target;
target=target.left;
}
cur.val=target.val;
if(targetParent.left==target){
targetParent.left=target.right;
}
else{
targetParent.right=target.right;
}
}
}
5.6 性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
5.7 和 java 类集的关系
TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set;实际上用的是红黑树,而红黑树是一棵近似平衡的二叉搜索树,即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证。