数据结构 C 代码 7.2: 邻接表及广度优先遍历
一.邻接表
邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。
对于无向图来说,使用邻接表进行存储也会出现数据冗余,表头结点A所指链表中存在一个指向C的表结点的同时,表头结点C所指链表也会存在一个指向A的表结点。[1]
注意:
n个顶点e条边的无向图的邻接表表示中有n个顶点表结点和2e个边表结点。(换句话说,每条边(i,j)在邻接表 中出现两次:一次在关于i的邻接表中,另一次在关于j的邻接表中)
二.代码
1.
int* visitedPtr;
//定义图
typedef struct Graph{
int** connections;
int numNodes;
} *GraphPtr;
//图的初始化
GraphPtr initGraph(int paraSize, int** paraData) {
int i, j;
GraphPtr resultPtr = (GraphPtr)malloc(sizeof(struct Graph));
resultPtr -> numNodes = paraSize;
//resultPtr -> connections = (int**)malloc(paraSize * paraSize * sizeof(int));
resultPtr -> connections = (int**)malloc(paraSize * sizeof(int*));
for (i = 0; i < paraSize; i ++) {
resultPtr -> connections[i] = (int*)malloc(paraSize * sizeof(int));
for (j = 0; j < paraSize; j ++) {
resultPtr -> connections[i][j] = paraData[i][j];
}//Of for j
}//Of for i
return resultPtr;
}/
typedef struct GraphNodeQueue{
int* nodes;
int front;
int rear;
}GraphNodeQueue, *QueuePtr;
//初始化队列
QueuePtr initQueue(){
QueuePtr resultQueuePtr = (QueuePtr)malloc(sizeof(struct GraphNodeQueue));
resultQueuePtr->nodes = (int*)malloc(QUEUE_SIZE * sizeof(int));
resultQueuePtr->front = 0;
resultQueuePtr->rear = 1;
return resultQueuePtr;
}//Of initQueue
//判断队列是否为空
bool isQueueEmpty(QueuePtr paraQueuePtr){
if ((paraQueuePtr->front + 1) % QUEUE_SIZE == paraQueuePtr->rear) {
return true;
}//Of if
return false;
}
//在队列里增加一个节点
void enqueue(QueuePtr paraQueuePtr, int paraNode){
if ((paraQueuePtr->rear + 1) % QUEUE_SIZE == paraQueuePtr->front % QUEUE_SIZE) {
printf("Error, trying to enqueue %d. queue full.\r\n", paraNode);
return;
}
paraQueuePtr->nodes[paraQueuePtr->rear] = paraNode;
paraQueuePtr->rear = (paraQueuePtr->rear + 1) % QUEUE_SIZE;
}
//删除一个元素并返回
int dequeue(QueuePtr paraQueuePtr){
if (isQueueEmpty(paraQueuePtr)) {
printf("Error, empty queue\r\n");
return NULL;
}
paraQueuePtr->front = (paraQueuePtr->front + 1) % QUEUE_SIZE;
//printf("dequeue %d ends.\r\n", paraQueuePtr->nodes[paraQueuePtr->front]);
return paraQueuePtr->nodes[paraQueuePtr->front];
}2.邻接表的结构体定义
typedef struct AdjacencyNode {
int column;
AdjacencyNode* next;
}AdjacencyNode, *AdjacentNodePtr;
typedef struct AdjacencyList {
int numNodes;
AdjacencyNode* headers;
}AdjacencyList, *AdjacencyListPtr3.构建邻接表
AdjacencyListPtr graphToAdjacentList(GraphPtr paraPtr) {
int i, j, tempNum;
AdjacentNodePtr p, q;
tempNum = paraPtr->numNodes;
AdjacencyListPtr resultPtr = (AdjacencyListPtr)malloc(sizeof(struct AdjacencyList));
resultPtr->numNodes = tempNum;
resultPtr->headers = (AdjacencyNode*)malloc(tempNum * sizeof(struct AdjacencyNode));
for (i = 0; i < tempNum; i ++) {
//Initialize headers.
p = &(resultPtr->headers[i]);
p->column = -1;
p->next = NULL;
for (j = 0; j < tempNum; j ++) {
if (paraPtr->connections[i][j] > 0) {
//Create a new node.
q = (AdjacentNodePtr)malloc(sizeof(struct AdjacencyNode));
q->column = j;
q->next = NULL;
p->next = q;
p = q;
}
}
}
return resultPtr;
}4.打印邻接表
void printAdjacentList(AdjacencyListPtr paraPtr) {
int i;
AdjacentNodePtr p;
int tempNum = paraPtr->numNodes;
printf("This is the graph:\r\n");
for (i = 0; i < tempNum; i ++) {
p = paraPtr->headers[i].next;
while (p != NULL) {
printf("%d, ", p->column);
p = p->next;
}//Of while
printf("\r\n");
}
}5.广度优先遍历
void widthFirstTranverse(AdjacencyListPtr paraListPtr, int paraStart){
printf("width first \r\n");
//Use a queue to manage the pointers
int i, j, tempNode;
AdjacentNodePtr p;
i = 0;
visitedPtr = (int*) malloc(paraListPtr->numNodes * sizeof(int));
for (i = 0; i < paraListPtr->numNodes; i ++) {
visitedPtr[i] = 0;
}
QueuePtr tempQueuePtr = initQueue();
printf("%d\t", paraStart);
visitedPtr[paraStart] = 1;
enqueue(tempQueuePtr, paraStart);
// printf("After enqueue\r\n");
while (!isQueueEmpty(tempQueuePtr)) {
// printf("First while\r\n");
tempNode = dequeue(tempQueuePtr);
for (p = &(paraListPtr->headers[tempNode]); p != NULL; p = p->next) {
j = p->column;
// printf("j = %d \r\n", j);
if (visitedPtr[j])
continue;
printf("%d\t", j);
visitedPtr[j] = 1;
enqueue(tempQueuePtr, j);
}
}
printf("\r\n");
}6.测试函数
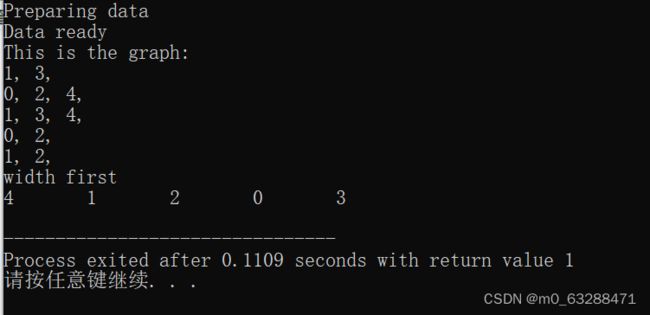
void testGraphTranverse() {
int i, j;
int myGraph[5][5] = {
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 1},
{1, 0, 1, 0, 0},
{0, 1, 1, 0, 0}};
int** tempPtr;
printf("Preparing data\r\n");
tempPtr = (int**)malloc(5 * sizeof(int*));
for (i = 0; i < 5; i ++) {
tempPtr[i] = (int*)malloc(5 * sizeof(int));
}//Of for i
for (i = 0; i < 5; i ++) {
for (j = 0; j < 5; j ++) {
//printf("i = %d, j = %d, ", i, j);
//printf("%d\r\n", tempPtr[i][j]);
tempPtr[i][j] = myGraph[i][j];
//printf("i = %d, j = %d, %d\r\n", i, j, tempPtr[i][j]);
}//Of for j
}//Of for i
printf("Data ready\r\n");
GraphPtr tempGraphPtr = initGraph(5, tempPtr);
AdjacencyListPtr tempListPtr = graphToAdjacentList(tempGraphPtr);
printAdjacentList(tempListPtr);
widthFirstTranverse(tempListPtr, 4);
}7.运行结果
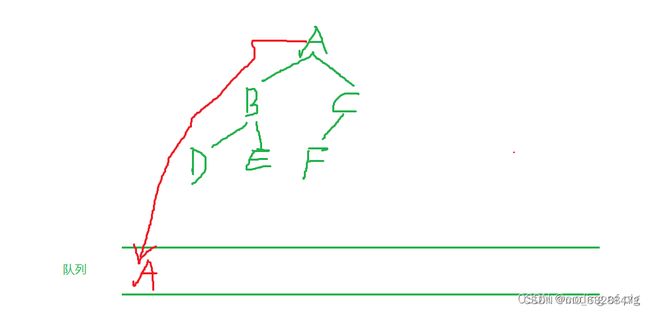
首先来说一下广度优先遍历,看名称很高大上的样子,其实它的原理跟树的层次遍历几乎一模一样。那么我就以树的层次遍历简单说明一下原理。
要实现层次遍历需要创建队列作为辅助。
层次遍历收先将根结点入队,如下图
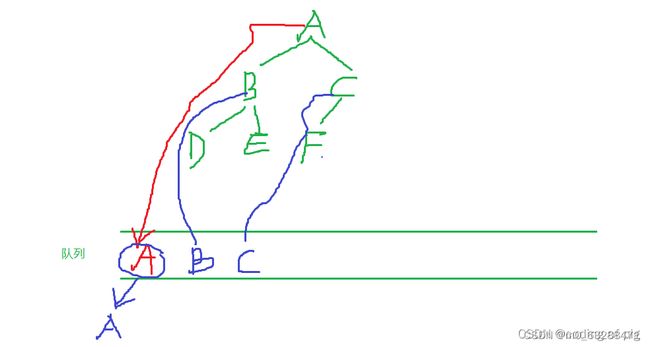
把B出队,将B的左右儿子入队,也就是谁出队就把谁的左右儿子入队: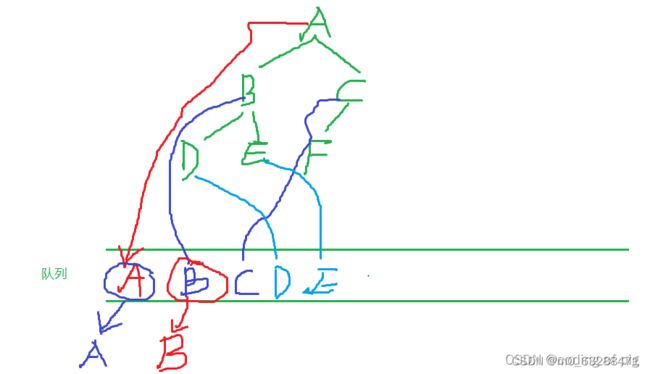
C出队,把C的左右儿子入队,依次循环下去.....,直到全部都输出,简单的来看一下,大家是否发现树的输出顺序是ABCDEF,也就是说一层一层的输出。这也是广度优先遍历的原理。