LeetCode每日一题02.01-02.07

2021.02.01-公平的糖果棒交换888

公平的糖果棒交换

题目描述：

题目解析：交换两个数组中的一个元素，保证两个数组的元素之和相等

简单暴力考虑就是计算Alice和Bob各自的糖果之和，然后求差，对于大的那一个从最大值x开始找小的那一个里面有没有值等于=x-差值/2（大的与小的相差2，那么大的-1，小的+1，则大的==小的）
时间复杂度：O(N*M)，N和M分别为Alice和Bob的糖果数量即两个数组的元素个数
空间复杂度为：O(2) 创建了一个两个元素的一维数组

public class FairCandySwap {
    /**
     * 使用暴力枚举解决问题
     * @param A
     * @param B
     * @return
     */
    public int[] fairCandySwap(int[] A, int[] B) {
        // 分别求A和B数组元素之和
        // 使用stream求和效率不高
        int sumA = Arrays.stream(A).sum();
        int sumB = Arrays.stream(B).sum();
        if (sumA > sumB) {
            // 对A进行大小排序
            Arrays.sort(A);
            return findResult(A, B, sumA, sumB, true);
        } else {
            Arrays.sort(B);
            return findResult(B, A, sumB, sumA, false);
        }
    }

    private int[] findResult(int[] A, int[] B, int sumA, int sumB, boolean flag) {
        int[] result = new int[2];
        // 求差值（题设中指明A和B元素之和不一致）
//        int diffValue = sumA > sumB ? sumA - sumB : sumB - sumA;
        int diffValue = sumA - sumB;
        // 从末尾遍历A，在B中找==A中元素-diffValue/2的值
        for (int i = A.length - 1; i >= 0; i--) {
            int element = A[i] - diffValue/2;
            for (int j = B.length - 1; j >= 0; j--) {
                if (B[j] == element) {
                    int oldA = A[i];
                    int oldB = B[j];
                    // 交换元素
                    int temp = B[j];
                    B[j] = A[i];
                    A[i] = temp;
                    if ((sumA - oldA + A[i]) == (sumB - oldB + B[j])) {
                        // 交换的是B的大的值，输出的时候A在前，B在后
                        if (!flag) {
                           temp = oldB;
                           oldB = oldA;
                           oldA = temp;
                        }
                        result[0] = oldA;
                        result[1] = oldB;
                        break;
                    }
                }
            }
        }
        return result;
    }

    public static void main(String[] args) {
        int[] A = {1,2,5};
        int[] B = {2,4};
        FairCandySwap fairCandySwap = new FairCandySwap();
        System.out.println(Arrays.toString(fairCandySwap.fairCandySwap(A, B)));
    }
}

参考https://leetcode-cn.com/problems/fair-candy-swap/solution/gong-ping-de-tang-guo-jiao-huan-by-leetc-tlam/

发现处理思路一致，只不过对于查找需要交换的元素这块处理大佬更简洁些，计算公式：sumA - x + y = sumB +x - y 转换成x = y + (sumA - sumB)/2; 直接将A数组的元素导入到集合中，遍历B，判断A中是否有值==B[j] + (sumA-sumB)/2即可

时间复杂度：O(n+m)，表示两次求和

空间复杂度：O(n)，n为A的长度，表示存储A元素的哈希set集合

    /**
     * 使用集合存储A，遍历B找到b[j] + (sumA - sumB)/2 的值在集合中存在
     * @param A
     * @param B
     * @return
     */
    public int[] fairCandySwap(int[] A, int[] B) {
        int sumA = Arrays.stream(A).sum();
        int sumB = Arrays.stream(B).sum();

        // 将A元素放入集合中，使用hashSet集合（先hash再查找速度更快）
        Set<Integer> ASet = new HashSet<>();
        for (int element : A) {
            ASet.add(element);
        }

        // 定义返回数组
        int[] result = new int[2];
        
        // 遍历B
        for (int element : B) {
            int x = element + (sumA - sumB) / 2;
            if (ASet.contains(x)) {
                result[0] = x;
                result[1] = element;
                break;
            }
        }
        return result;
    }

总结：发现问题的解决关键点很重要，多分析然后理出思路，再考虑如何优化。例如如果发觉了可以用公式，那就会想说用两个循环；但一想两个循环其实没必要，可以一个数组存集合；那存什么集合比较快？hashSet！欸结果出来了。
所以要先发现关键点，然后梳理实现路线，最后看哪里可以优化

2021.02.02-替换后的最长重复字符424

替换后的最长重复字符

题目描述：

题目解析：遍历数组通过替换指定个数的元素，得到最长重复子串长度

想到了双指针，从头开始遍历数组，遇到不一样的替换成一样的，并且k–，直到k==0，然后判断是否是最长重复子串（得到所有重复子串，然后计算长度）如果不是遍历下一个不一样的字符，遇到不一样的替换

参考https://leetcode-cn.com/problems/longest-repeating-character-replacement/solution/ti-huan-hou-de-zui-chang-zhong-fu-zi-fu-n6aza/

对于双指针，找到其最远的左端点的位置，满足该区间内除了出现次数最多的那一类字符之外，剩余的字符（即非最长重复字符）数量不超过 k个

漏掉了一个点：字符串中所有的字符都是大写英文字母，这意味着最小为A，最大为Z

对于自己的思路，双指针没有问题，但是真的去替换这块处理有问题，因为第一次替换之后得到了一个子串。那后续left移动之后，就无法恢复前面的串，除非重新s再替换，替换操作时间复杂度高，而且right需要从left+1开始重新遍历

参考官方题解，可知其实不需要多余做这个替换的操作，直接计算每个字符出现的次数，然后最大子串长度maxnum=max{maxnum,当前字符的出现频次}，right往右遍历的时候判断right-left是否大于maxnum+k【这样不会拘泥于只能求left元素的最大重复子串，而是求right-left之间最多出现元素的最大重复子串】。如果是说明已经是left字符的最大重复子串，移动left【注意left当前字符的频次需要–，然后再left++】

时间复杂度：O(N)，N为字符串s的长度

空间复杂度：O(A)，A为字符串s出现字符的范围（26个字符就是26）就算s中只有A和Z，但是数组都是一样要初始化26个坑位的。【除非改成哈希表，这样的话空间复杂度就是字符串s出现字母的种类数】

public class CharacterReplacement {

    /**
     * 使用双指针法/滑动窗口法，解决最长重复字串问题
     * @param s
     * @param k
     * @return
     */
    public int characterReplacement(String s, int k) {
        int length = s.length();
        // 字符串为空或者只有一个字符
        if (length < 2) {
            return length;
        }

        // 将字符串转为字符数组
        char[] charArray = s.toCharArray();

        // 定义存储字符频次的数组
        // 因为字符串由大写字母构成，所以最大为Z，最小为A，长度为26，
        // 将字母作为count数组的下标，需要减去'A'，保证结果在0-25内
        int[] count = new int[26];

        // 定义左右指针，初始为0
        int left = 0;
        int right = 0;

        // 定义最大的元素个数
        int maxNum = 0;
//        // 记录最大的重复子串长度
//        int result = 0;

        // 遍历字符数组，移动right，获取最大的重复子串长度
        while (right < length) {
            // 初始right=0
            count[charArray[right] - 'A']++;
            // 获取当前窗口重复元素的最大个数
            maxNum = Math.max(maxNum, count[charArray[right] - 'A']);
            right++;

            // 判断right-left是否已经超出maxNum+k，
            // 即无法再替换元素增大right-left窗口中最多连续重复字串的长度
            // 每次while进来if最多被执行一次（if无需换成while，因为只需要知道最大重复子串，下一窗口的长度最小==上一窗口的长度）
            if (right - left > maxNum + k) {
                // left右移并left元素频次--
                count[charArray[left] - 'A']--;
                // right不做任何操作，因为刚好前面右移一位，left++一次，
                // 此时子串长度刚好等于上一个窗口长度【目标是找到比这个更长的长度】
                // right没必要从left重新遍历一次，因为找的是最大值，只要能比上一个窗口大即可
                left++;
            }
//            result = Math.max(result, right - left);
        }
        // 无需多一个变量去每次换窗口的时候获取res和right-left的最大值，
        // 因为最大的永远是right-left（每一次换窗口的长度最小值为上一个窗口的长度最大值，
        // right-left最小等于之前的最大值，只会保持不变或越来越大）
        // 除非想知道最长重复且最早出现的子串是多少的情况下，需要记录最长的时候的左右下标
//        return result;
        return right - left;
    }

    public static void main(String[] args) {
        CharacterReplacement characterReplacement = new CharacterReplacement();
        String s = "ABAA";
        System.out.println(characterReplacement.characterReplacement(s,1));
    }
}

2021.02.03-滑动窗口中位数480

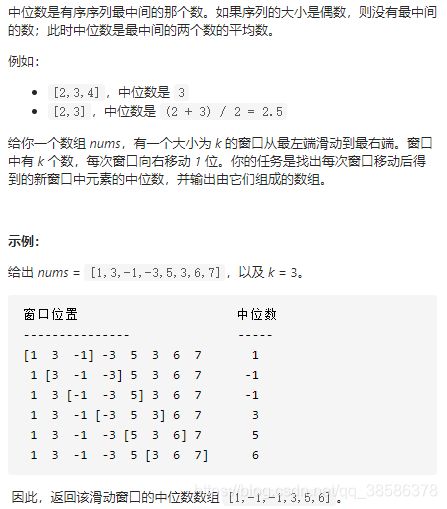
滑动窗口中位数

题目描述：

题目解析：题意很明确，就是给一个k值和一个数组，将数组从头开始遍历，每过k个，求一下当前k个值的中位数，注意求的时候需要对这k个值先做一下大小排序

如果k是偶数，那么中位数为中间两个数的平均数，即和/2，如果有序的情况下是(right-left)/2和(right-left)/2+1

如果k是奇数，那么中位数为中间的那个数，如果有序的情况下是（right-left）/2对应的值

难点在于，真的要滑动一次窗口，都重新对right-left中的数进行排序么，中间有k-1个数是已经排过序的，所以是否可使用插入排序方法，可以试试
时间复杂度：O((length-k+1)^3) 遍历这么多次，里面又嵌套了时间复杂度为O(n^2)的插入排序
空间复杂度：O(length-k+1) + O(k) 前者是存放中位数创建的一维数组，后者是k大小的子数组

public class MedianSlidingWidow {
    /**
     * 利用双指针+插入排序完成
     * 双指针控制数组的左右边界
     * 插入排序控制k大小的窗口中元素有序，便于求中位数并输出到一维数组中
     * 数组的大小根据枚举发现规律：nums.length - k + 1（题设中指明k小于非空数组的length）
     * @param nums
     * @param k
     * @return
     */
    public double[] medianSlidingWindow(int[] nums, int k) {
        // 数组长度
        int length = nums.length;
        if (length < 2) {
            // k == 0
            return new double[] {nums[0]};
            // 实际上k应该大于0才是，不然窗口为0，就没有中位数
        }
        // 确定结果数组的长度
        double[] result = new double[length - k + 1];
        // 定义左右指针的初始值
        int left = 0;
        // 注意因为数组下标从0开始，所以右指针值为k-1
        int right = k - 1;
        // 应该从头开始遍历，使用冒泡排序，对其进行排序，但是相对来讲插入排序更好些
//        int right = 1;
        // 开始遍历数组nums
        while (right < length) {
            // 对现在k个值的窗口的元素排序并取中位数
            // 排序，第一次比较麻烦循环次数比较多，之后都是一次
            // 发现了一个大问题，不能对原数组排序，因为滑动窗口是在原数组上进行的，排序之后数组元素就变了

            // 计算中位数
            result[left] = insertOrder(nums, left, right);
            left++;
            right++;
        }
        return result;
    }

    /**
     * 插入排序并求中位数
     * @param array
     * @param left
     * @param right
     * @return
     */
    private double insertOrder(int[] array, int left, int right) {
        // 拷贝数组
//        System.out.println(left);
//        System.out.println(right);
        int[] newArray = new int[right - left + 1];
        System.arraycopy(array, left, newArray, 0, newArray.length);
//        System.out.println(Arrays.toString(newArray));
        // 注意此时是一个新的数组，长度一直为right-left+1，从0开始
        for (int i = 0; i < newArray.length; i++) {
            int temp = newArray[i];
            int j = i - 1;
            for (; j >= 0; j--) {
                // 发现大值，往右移动
                if (newArray[j] > temp) {
                    newArray[j+1] = newArray[j];
                } else {
                    break;
                }
            }
            // 若发生移动，则将小值temp移过来
            if (newArray[j+1] != temp) {
                newArray[j+1] = temp;
            }
        }
        // 注意结果取double，要在和的两个值先强转为double
        return (right - left) % 2 == 0 ? newArray[(right - left) / 2] : ((double)newArray[(right - left) / 2] + (double)newArray[(right - left) / 2 + 1]) / 2;
    }

    public static void main(String[] args) {
        MedianSlidingWidow medianSlidingWidow = new MedianSlidingWidow();
//        int[] nums = {1,3,-1,-3,5,3,6,7};
        int[] nums = {1,4,2,3};
        int k = 4;
        System.out.println(Arrays.toString(medianSlidingWidow.medianSlidingWindow(nums, k)));
    }
}

方法可行，就是要对k个元素的数组排序排序nums.length-k+1次，在nums特别大且k比较小的情况下，时间消耗特别严重，LeetCode提示超出时间限制qaq

直接抄了LeetCode的答案（https://leetcode-cn.com/problems/sliding-window-median/solution/hua-dong-chuang-kou-zhong-wei-shu-by-lee-7ai6/），因为目前答案也看不懂，只看懂了双优先队列得到中位数的妙操作orz

 public double[] medianSlidingWindow(int[] nums, int k) {
        DualHeap dh = new DualHeap(k);
        for (int i = 0; i < k; ++i) {
            dh.insert(nums[i]);
        }
        double[] ans = new double[nums.length - k + 1];
        ans[0] = dh.getMedian();
        for (int i = k; i < nums.length; ++i) {
            dh.insert(nums[i]);
            dh.erase(nums[i - k]);
            ans[i - k + 1] = dh.getMedian();
        }
        return ans;
    }
}

class DualHeap {
    // 大根堆，维护较小的一半元素
    private PriorityQueue<Integer> small;
    // 小根堆，维护较大的一半元素
    private PriorityQueue<Integer> large;
    // 哈希表，记录「延迟删除」的元素，key 为元素，value 为需要删除的次数
    private Map<Integer, Integer> delayed;

    private int k;
    // small 和 large 当前包含的元素个数，需要扣除被「延迟删除」的元素
    private int smallSize, largeSize;

    public DualHeap(int k) {
        this.small = new PriorityQueue<Integer>(new Comparator<Integer>() {
            @Override
            public int compare(Integer num1, Integer num2) {
                return num2.compareTo(num1);
            }
        });
        this.large = new PriorityQueue<Integer>(new Comparator<Integer>() {
            @Override
            public int compare(Integer num1, Integer num2) {
                return num1.compareTo(num2);
            }
        });
        this.delayed = new HashMap<Integer, Integer>();
        this.k = k;
        this.smallSize = 0;
        this.largeSize = 0;
    }

    public double getMedian() {
        return (k & 1) == 1 ? small.peek() : ((double) small.peek() + large.peek()) / 2;
    }

    public void insert(int num) {
        if (small.isEmpty() || num <= small.peek()) {
            small.offer(num);
            ++smallSize;
        } else {
            large.offer(num);
            ++largeSize;
        }
        makeBalance();
    }

    public void erase(int num) {
        delayed.put(num, delayed.getOrDefault(num, 0) + 1);
        if (num <= small.peek()) {
            --smallSize;
            if (num == small.peek()) {
                prune(small);
            }
        } else {
            --largeSize;
            if (num == large.peek()) {
                prune(large);
            }
        }
        makeBalance();
    }

    // 不断地弹出 heap 的堆顶元素，并且更新哈希表
    private void prune(PriorityQueue<Integer> heap) {
        while (!heap.isEmpty()) {
            int num = heap.peek();
            if (delayed.containsKey(num)) {
                delayed.put(num, delayed.get(num) - 1);
                if (delayed.get(num) == 0) {
                    delayed.remove(num);
                }
                heap.poll();
            } else {
                break;
            }
        }
    }

    // 调整 small 和 large 中的元素个数，使得二者的元素个数满足要求
    private void makeBalance() {
        if (smallSize > largeSize + 1) {
            // small 比 large 元素多 2 个
            large.offer(small.poll());
            --smallSize;
            ++largeSize;
            // small 堆顶元素被移除，需要进行 prune
            prune(small);
        } else if (smallSize < largeSize) {
            // large 比 small 元素多 1 个
            small.offer(large.poll());
            ++smallSize;
            --largeSize;
            // large 堆顶元素被移除，需要进行 prune
            prune(large);
        }
    }

等看懂了回来补充。。

2021.02.04-子数组最大平均数I643

子数组最大平均数 I

题目描述：

题目解析：滑动窗口方法

从数组开始开始遍历，窗口大小为k，left和right初始值为0，right往右加，直到right-left+1=k，right++的过程加和所有right对应的值，记作sum，作为当前的最大值（值最大即平均值最大）

left++，right++，sum=sum-nums[left]+nums[right]，比较与上一次max的大小，若大于则将这个sum作为最大值

需要注意的：
1，当移动left的时候，sum要记得减去nums[left]，然后再left++

2，另外因为数据范围是[-10000,10000]，所以可能k个值的和结果小于0，所以最大值max初始值不能为0，设置为-10000*k

3， 返回值因为是double类型，所以做除法的时候记得给商加double进行类型强转

时间复杂度O(nums.length)，即数组大小

空间复杂度O(1) 一个变量的空间

public class FindMaxAverage {
    /**
     * 使用滑动窗口解决问题
     * @param nums
     * @param k
     * @return
     */
    public double findMaxAverage(int[] nums, int k) {
        // 数组长度最小为1
        int length = nums.length;
        // 没有必要，因为底下的循环是包含length==1的情况的
//        // 当数组长度为1的时候，k==n，最后平均值为数组的唯一元素
//        if (length < 2) {
//            return nums[0];
//        }

        // 初始化左右指针
        int left = 0;
        int right = 0;
        // 初始化最大值，最大值不能是0，因为可能数组中的最大值小于0
        // 因为题中说明数据范围为[-10000,10000]，那么最小值为-10000*k
        // (注意根据数据的边界值给出可能的最大值最小值）
        int max = -10000 * k;
        // 初始化和
        int sum = 0;

        // 遍历数组
        while (right < length) {
            // 构建窗口 不用if的原因是第一次会跑去求max和底下的sum
            while (right - left + 1 <= k) {
                sum += nums[right++];
            }
            // k大小的窗口构建完毕，找最大值
            max = Math.max(max, sum);
            // 左指针往右移动一位，此时右指针已经移动了一位
            // 之后都是while只满足一次，然后左右指针同时往右移动
            // 别忘记做减法（将左值针指向的值减去）
            sum -= nums[left++];
//            left++; // 单纯left++是不对的，要记得减去left对应的值再left++
        }
        // 注意结果返回类型为double，需要对max加double进行类型强转
        return (double)max / k;
    }

    public static void main(String[] args) {
        FindMaxAverage findMaxAverage = new FindMaxAverage();
        int[] nums = {-1,-12,-5,-6,-50,-3};
        int k = 4;
        System.out.println(findMaxAverage.findMaxAverage(nums, k));
    }
}

参考https://leetcode-cn.com/problems/maximum-average-subarray-i/solution/zi-shu-zu-zui-da-ping-jun-shu-i-by-leetc-us1k/

直接使用滑动窗口法，时间复杂度O(N)和空间复杂度O(1)不变

    /**
     * 使用滑动窗口法解决问题
     * @param nums
     * @param k
     * @return
     */
    public double findMaxAverage(int[] nums, int k) {
        int sum = 0;
        int length = nums.length;
        // 第一个窗口
        for (int i = 0; i < k; i++) {
            sum += nums[i];
        }
        // 记录最大值，初始值直接为第一个窗口的值（无需定义max的初始值为一个很小的无意义的数，
        // 而是定义为有意义的第一个窗口元素和
        int max = sum;
        // 开始滑动窗口
        for (int i = k; i < length; i++) {
            // 滑动窗口，减左值加右值，此时左值为i-k
            sum = sum - nums[i - k] + nums[i];
            // 求较大值
            max = Math.max(max, sum);
        }
        // 类型转换除了直接加double，也可以*1.0进行隐式类型转换
        return 1.0 * max / k;
    }

显示速度要更快点，应该是在sum求值？之前的是做两次运算，将这个代码中sum拆分为一步减和一步加，速度同上一个代码（所以基本运算这里能合并尽量合并）

2021.02.05-尽可能使字符串相等1208

尽可能使字符串相等

题目描述：

对于示例2，因为diffValue中的每个值都是2，而cost为3，所以最长子串长度只能是1（否则两个的话就会是4，大于3）
看不懂题orz，直奔题解
摘自：https://leetcode-cn.com/problems/get-equal-substrings-within-budget/solution/jin-ke-neng-shi-zi-fu-chuan-xiang-deng-b-higz/

    /**
     * 使用双指针法解决问题，主要是从s和t转化为一个diffValue数组求最长子串
     * 时间复杂度：O(n) 空间复杂度：O(n) n为diffValue数组长度即s和t的长度
      * @param s
     * @param t
     * @param maxCount
     * @return
     */
    public int equalSubstring(String s, String t, int maxCount) {
        int length = s.length();
        // 定义一个length长的数组存储s和t的ASCII码值之差
        int[] diffValue = new int[length];
        // 赋值
        for (int i = 0; i < length; i++) {
            diffValue[i] = Math.abs(s.charAt(i) - t.charAt(i));
        }

        // 定义最长返回值
        int maxLength = 0;
        // 定义左右指针
        int left = 0;
        int right = 0;
        // 定义总和
        int sum = 0;

        // 遍历diffValue数组
        while (right < length) {
            sum += diffValue[right];
            while (sum > maxCount) {
                // 左指针右移
                sum -= diffValue[left];
                left++;
            }
            maxLength = Math.max(maxLength, right - left + 1);
            right++;
        }
        return maxLength;
    }

读懂题意进行合理变形转为自己熟知的场景，并解决

2021.02.06-可获得的最大点数1423

可获得的最大点数

题目描述：

题目解析：

依旧是求数组中k个值的最大值，不同的是不再是滑动窗口，一边固定一边移动；而是两头都可移动

那么就是双指针，然后left=0，right=cardPoints.length-1，比较left和right对应的值大小，取大保存为sum，记录k–，right–，继续比较left和right对应的值每次都取较大值直到k=0为止，返回sum

存在的问题：如果是{1,100,13,2,2,100} k=3那照现在的处理逻辑是，100+2+2，这是不对的

正确的逻辑是：1+100+100，并非每次取最大值，而是得保证最后取最大值

    /**
     * 双指针法
     * @param cardPoints
     * @param k
     * @return
     */
    public int maxScore(int[] cardPoints, int k) {
        int length = cardPoints.length;
        // 当k==length的时候，结果返回数组元素之和
        if (k == length) {
            return Arrays.stream(cardPoints).sum();
        }

        // 定义左右指针
        int left = 0;
        int right = length - 1;
        // 定义最大值，因为根据题设数组元素都是大于0的，所以设置初始值为0
        int sum = 0;

        // 遍历数组
        while (left <= right) {
            // 比较左右指针的值的大小，sum加一个大值肯定大于sum加一个小值
            if (cardPoints[left] > cardPoints[right]) {
                sum += cardPoints[left++];
            } else {
                sum += cardPoints[right--];
            }
            // 得到一个值，k--
            k--;
            if (k == 0) {
                break;
            }
        }
        return sum;
    }

看了题解，这也能滑是我万万没想到的qaq
https://leetcode-cn.com/problems/maximum-points-you-can-obtain-from-cards/solution/ke-huo-de-de-zui-da-dian-shu-by-leetcode-7je9/

两种滑法，一种是滑动不要的n-k个，求最小值，然后数组总值-最小值就是目标最大值

时间复杂度O(n)

空间复杂度O(1)

但是性能没有第二种方法好，主要是stream运算耗费性能

    /**
     * 逆向滑动窗口
     * @param cardPoints
     * @param k
     * @return
     */
    public int maxScore(int[] cardPoints, int k) {
        int length = cardPoints.length;
        // 逆向滑动窗口大小
        int size = length - k;
        // 初始
        int sum = 0;
        for (int i = 0; i < size; i++) {
            sum += cardPoints[i];
        }
        // 初始最小值为sum
        int min = sum;
        // 遍历数组
        for (int i = size; i < length; i++) {
            // 右移一位，就得减去左边的元素值
            sum += cardPoints[i] - cardPoints[i - size];
            min = Math.min(min, sum);
        }
        return Arrays.stream(cardPoints).sum() - min;
    }

另外一种是正向滑，窗口是前k个和后k个之间滑动，求最大值

时间复杂度O(n)

空间复杂度O(1)

    /**
     * 滑动窗口法
     * @param cardPoints
     * @param k
     * @return
     */
    public int maxScore(int[] cardPoints, int k) {
        int length = cardPoints.length;
        int sum = 0;
        // 初始为前k个元素之和
        for (int i = 0; i < k; i++) {
            sum += cardPoints[i];
        }
        // 最大值
        int max = sum;
        // 遍历数组
        for (int i = 0; i < k; i++) {
//            // 取右
//            sum += cardPoints[length - i - 1];
//            // 去左边最右一位
//            sum -= cardPoints[k - i - 1];
            // 两个运算整合在一起，性能更高
            sum = sum + cardPoints[length - i - 1] - cardPoints[k - i - 1];
            max = Math.max(max, sum);
        }
        return max;
    }

2021.02.07-非递减数列665

题目描述：

题目解析：

遍历数组nums，判断是否可通过改变一个元素/不做任何改变，得到一个递减的序列，即nums[i] <= nums[i+1] 注意是只要相邻的元素满足即可，并非整个序列是一个有序递减序列

数组法：

i=0开始，给个标志位，如果找到nums[i]>nums[i+1]，flag=true，并且判断i是否大于0且nums[i-1]>nums[i+1]，如果是则nums[i+1]=nums[i]，因为此时i+1必须调整值，再继续判断i+1与后续元素的大小

如果不满足的话直接调整nums[i]满足nums[i-1]<=nums[i]<=nums[i+1]

时间复杂度O(n)

空间复杂度O(1)

   /**
     * 使用数组解决问题
     * @param nums
     * @return
     */
    public boolean checkPossibility (int[] nums) {
        // 数组长度在1-10000
        int length = nums.length;

        // 当数组元素只有一个的时候，直接返回true
        if (length == 1) {
            return true;
        }

        // 定义标识符，表明是否有找到nums[left]>nums[right]
        boolean flag = false;

        // 审错题意，直接相邻的两两进行比较，满足nums[i]<=nums[i+1]即可
        // 注意i的边界，因为会有i+1，所以i
        for (int i = 0; i < length - 1; i++) {
            // 发现第一个
            if (!flag && nums[i] > nums[i+1]) {
                flag = true;
                // 得注意边界值，如果是边界值i==0的话，直接记录flag=true即可
                // a b c d，如果ac，得调整c，调整b没用，因为找不到
                // 一个值可以满足大于a，且小于c(c是小于a的），只能调整c>=b才可
                if (i > 0 && nums[i + 1] < nums[i - 1]) {
                    // 将小值调整为大值
                    nums[i + 1] = nums[i];
                }
                // 进行下一组循环
                continue;
            }
            if (flag && nums[i] > nums[i+1]) {
                return false;
            }
        }
        // flag==false或者flag==true
        return true;
    }

参考：https://leetcode-cn.com/problems/non-decreasing-array/solution/fei-di-jian-shu-lie-by-leetcode-solution-zdsm/

优化一下代码，使用计数器计算调整元素的次数，根据count大于1返回结果为false

    /**
     * 记录改变元素的次数，由此判断是否为true
     * @param nums
     * @return
     */
    public boolean checkPossibility (int[] nums) {
        int length = nums.length;
        int count = 0;
        for (int i = 0; i < length - 1; i++) {
            if (nums[i] > nums[i+1]) {
                count++;
                if (count > 1) {
                    return false;
                }
                if (i > 0 && nums[i-1] > nums[i+1]) {
                    nums[i+1] = nums[i];
                }
            }
        }
        return true;
    }

总结

又一周过去了，这周主要是学习了使用滑动窗口法去解决问题。
读懂题意很重要，学会讲题转换为自己熟悉的点，继续加油，要更加有条理的梳理:)