【雷达原理】雷达信号级建模与仿真

前言

---

雷达信号形式多种多样，按照雷达的体制进行分类，有脉冲雷达和连续波雷达。脉冲雷达使用脉冲波形串，收发一体，在发射信号期间关闭接收机，其一般功率较大，作用距离较远，主要应用在军事领域，包括海陆空的监视、导航和武器制导等。
连续波雷达则连续发射电磁能量，收发分置，即信号的发射和接收同时进行，受限于收发天线间隔离等因素，发射功率不能过大，导致作用距离较近，适用于探测近距离目标，当前在民用市场的应用较多，特别是车载雷达领域。
连续波雷达可分为未调制连续波和调制连续波，未调制连续波雷达可以用来测量目标的径向速度和角位置，但无法提取目标的距离信息，因此，为了提取目标的距离信息，通常采用频率调制的方式。

一、LFMCW信号概述

线性调频连续波(Linear Frequency Modulated Continuous Wave，LFMCW)雷达通过对发射信号的频率进行线性调制，进而对目标回波信号进行处理，达到提取目标距离信息的目的。
随着线性调频连续波雷达的不断发展，作用距离较短使其在近距离场景的探测中有着很大的优势。通过总结该体制雷达的特点，可以最大程度的发挥其优点，避免因其缺点造成的影响。

1.1 优点

(1) 无距离盲区
线性调频连续波雷达采用双天线配置，收发天线同时工作，在发射信号的同时对目标反射的回波进行接收，而脉冲雷达则收发一体，具有一定的探测盲区。同时，线性调频连续波雷达信号的调制时间较长(带宽较大)，对近距离目标仍会存在差频，在探测近距离目标方面有着无可比拟的优势。

(2) 发射功率低，接收机灵敏度高
脉冲雷达由于发射短脉冲，其所需的峰值功率较高，易被敌方截获，而 LFMCW 雷达在一个调制周期内，其信号的时宽带宽积($BT$)大，雷达在整个调制周期内都处于低功率状态。

(3) 距离分辨率高
LFMCW 雷达将发射信号与接收信号进行混频以实现下变频，得到较小带宽的拍频信号，拍频信号在混频之前是大带宽信号，因此整个系统信号带宽可以做更高， 以便适用于较高距离分辨率的场景中。

(4) 结构简单
由于发射信号的调制时间占空比为100％，通过大时宽来获取能量，因此在近距离测距时不需要较大的电压，且低电压下工作使系统避免了高功率器件的使用，使系统体积变小，容易固态化，降低工程实现的代价。

1.2 缺点

(1) 作用距离短
由于LFMCW雷达的收发天线同时工作，为了避免发射天线的信号功率泄露到接收天线上，发射天线与接收天线需要有一定的隔离度，因而发射天线的功率不能太高，这就使得雷达的探测距离受到了限制。

(2) 距离-速度耦合
当线性调频连续波雷达采用单调频的发射信号时，目标与雷达有相对运动时，由模糊函数理论可知，会产生 距离一速度耦合 现象，该现象会在测距时产生偏差，影响最终参数估计的准确性，因此，距离一速度耦合现象是阻碍LFMCW雷达发展的主要原因之一。

二、LFMCW信号模型

LFMCW 雷达常见的调制方式可分为两种：1) 三角波调制方式； 2) 锯齿波调制方式， 这两种方式基本原理都是利用发射信号和目标回波的差频信号，经过信号处理实现目标距离的探测。本博文主要介绍锯齿波调频。

2.1 发射信号模型

当雷达的发射信号为经过正交调制的线性调频信号时，其数学表达式可表示为：

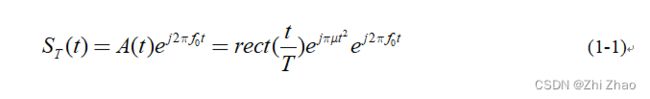
$A(t)$ 为复包络，其表达式如(1-2)所示，其中 $T$ 为脉冲的宽度，$\mu =B/T$ 为调频斜率，$B$ 为信号的带宽。

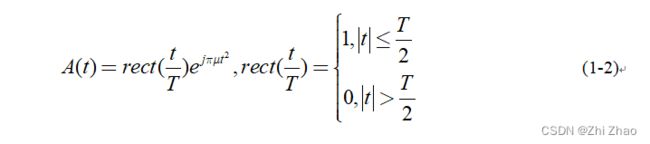
信号的相位为：

信号的瞬时频率为：

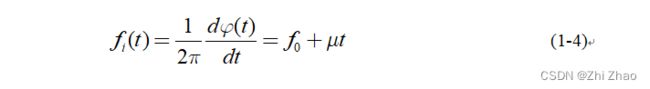
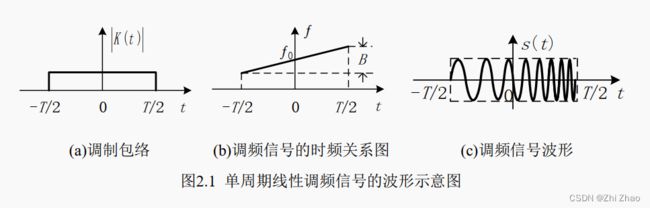
根据公式(1-2)可以画出LFM信号在单个调频周期内的包络如图2.1(a)，根据公式(1-4)可以画出LFM信号的频率随时间变化关系如图2.1(b)所示，一个调制周期内LFM信号的波形如图2.1© 所示。

2.2 接收信号模型

雷达产生的发射信号经过天线后，以电磁波的形式向空中辐射，当有目标存在时，电磁波会发生反射、折射等现象，其中一部分电磁波会沿原路返回，并被天线接收，这个信号被称为目标回波，即雷达的接收信号。
当雷达在 ′ 时刻向外发射调频连续波（电磁波），电磁波在空中飞行一段时间 $\tau$ 后，在"时刻到达接收天线，雷达发射信号与接收信号的关系如下图所示，由于时延$\tau$导致信号之间存在频率差为$f_b$，即差拍频率。

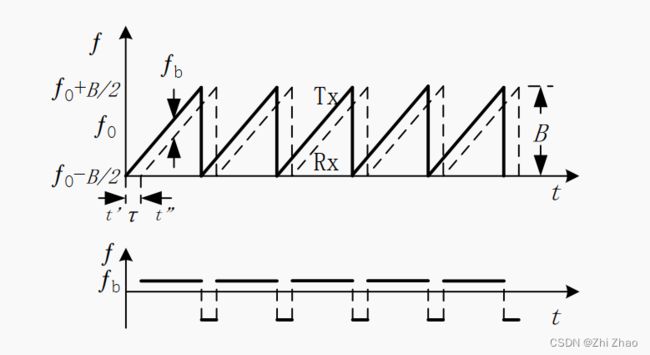
根据式(1-4)可知，雷达发射端的信号频率与时间变化呈线性关系，对于静止的目标，没有多普勒效应， 如果不考虑接收机内部噪声和外部环境噪声的干扰，接收端的频率和发射端的频率变化关系保持一致，只是延迟了时间 $\tau$。 因此，一个周期内目标回波信号的表达式可表示为：

2.3 信号混频

为了提取出差频信号，需要将发射信号(本振信号)与接收信号进行混频，混频的本质就是两个信号相乘。根据积化和差公式，两个角频率为 $w_1$和$w_2$的正弦信号相乘：

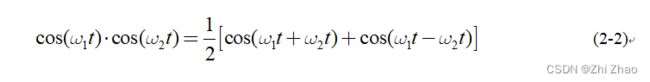
可产生角频率为 ($w_1+w_2$) 和($w_1-w_2$)的正弦波信号，频率相加的分量称为上变频，频率相减的分量称为下变频。发射信号与接收信号混频后，其中下变频部分是对后续信号处理有用的信号，其频率一般在MHz级别。

当雷达采用正交调制方式产生发射信号时，发射信号与接收信号经过混频器处理后，表达式为：

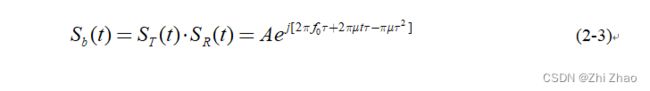
相比于直接调频方式，采用正交调制的调频方式在接收到回波信号进行混频后没有高频项，但正交调频电路的设计也相对复杂。

混频后，信号的频率为：

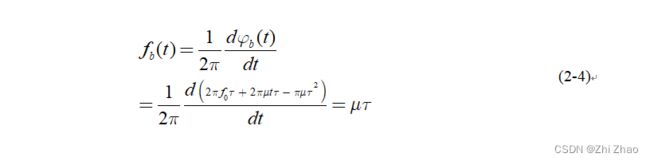
由上式可知，混频后信号的频率只与本振的调频斜率 $\mu$ 和回波信号的延迟时间 $\tau$ 有关，与其余的变量无关。

三、MATLAB仿真

3.1 仿真结果

(1) 利用MATLAB对中心频率为 $f_0=0$ 的线性调频信号进行仿真，依次为信号的实部、虚部、相位和频率。
(2) 利用MATLAB对中心频率为 $f_0=77GHz$ 的线性调频信号进行仿真，信号的时长为$T=100us$。

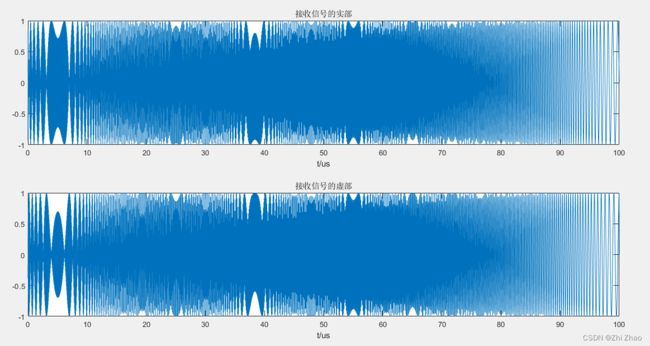
3.2 代码

clc;
clear;
close all;

%% LFM信号参数
B = 20e6;       % 带宽
T = 10e-6;      % 脉冲宽度
u = B/T;        % 调频斜率
fs = 2*B;       % 采样率
N = T*fs;       % 采样点数

%% LMF信号的基本特点
t = linspace(-T/2,T/2,N);

St = exp(1j*pi*u*t.^2);         % 没有中心频率的LFM信号
phaseT = pi*u*t.^2;             % 瞬时相位
Ft = u*t;                       % 瞬时频率
figure;
subplot(2,2,1);plot(t*1e6,real(St));xlabel('t/us');title('LFM信号实部');
subplot(2,2,2);plot(t*1e6,imag(St));xlabel('t/us');title('LFM信号虚部');
subplot(2,2,3);plot(t*1e6,phaseT);xlabel('t/us');title('LFM信号的相位变化');
subplot(2,2,4);plot(t*1e6,Ft);xlabel('t/us');title('LFM信号的频率变化');

clc;
clear;
close all;

%% LFM信号参数
B = 20e6;       % 带宽
T = 100e-6;      % 脉冲宽度
u = B/T;        % 调频斜率
fs = 2*B;       % 采样率
N = T*fs;       % 采样点数

c = physconst('LightSpeed');        % 光速
f0 = 77e9;                          % 载频
Lambda = c/f0;                      % 波长

%% 模拟信号
t = linspace(0,T,N);
Phase_t = @(f0,u,t) 2*pi*(f0*t+1/2*u*t.^2);        % LFM信号的相位表达式

Signal_Tx = rectpuls(t-T/2,T).*exp(1j*Phase_t(f0,u,t));        % 发射信号
figure;
subplot(2,1,1);plot(t,real(Signal_Tx));title('发射信号的实部');
subplot(2,1,2);plot(t,imag(Signal_Tx));title('发射信号的虚部');

R0 = 200;           % 静止目标
tao = 2*R0/c;       % 目标回波的时延
Signal_Rx = rectpuls(t-T/2,T).*exp(-1j*Phase_t(f0,u,(t-tao)));        % 接收信号
figure;
subplot(2,1,1);plot(t,real(Signal_Rx));title('接收信号的实部');
subplot(2,1,2);plot(t,imag(Signal_Rx));title('接收信号的虚部');

Signal_Mix = Signal_Tx.*Signal_Rx;
figure;
subplot(2,1,1);plot(t,real(Signal_Mix));title('混频后信号的实部');
subplot(2,1,2);plot(t,imag(Signal_Mix));title('混频后信号的虚部');

四、参考文献

[1] 刘贺. 线性调频连续波雷达信号处理研究及数据分析[D].西南交通大学,2017.
[2] 许成洋. 相控阵LFMCW雷达信号处理方法及实现[D].西安电子科技大学, 2020.