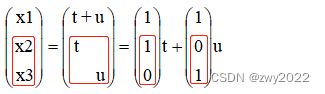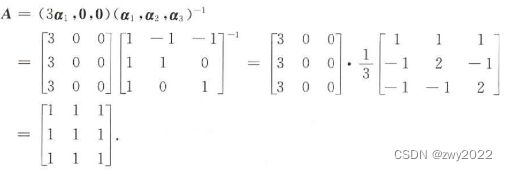线代第五章 特征值和特征向量 复习笔记

Aα=λα    n阶矩阵A×特征向量= 特征值×特征向量

A：n阶矩阵

α：一个n维列向量——矩阵A属于特征值λ的特征向量（特征向量α是非零向量）

λ：一个数——矩阵A的特征值

由Aα=λα移项得 λα-Aα=0→结合律得 (λE-A)α=0：

特征多项式 |λE-A|

特征方程 |λE-A|=0

由于α为非零向量|α|≠0，|λE-A|×|α|=0→|λE-A|=0  所有符合等式的λ即为特征值

齐次方程组 (λE-A)x=0

每一个特征值λ都对应一个齐次方程组→求特征向量α就转变为求齐次方程组的非零解。

常见题型一：给定n阶矩阵A，求其特征值和特征向量。

步骤

1、写出特征多项式（行列式）|λE-A|

2、根据特征方程 |λE-A|=0 解出矩阵A所有的特征值λi

3、分别将λi代入方程 (λE-A)x=0中，求得基础解系α1、α2…(一共n-r个解向量)

4、线性组合基础解系 k1α1+k2α2+…(k1、k2不全为零)，即为矩阵A属于特征值λi的所有特征向量

---

若基础解系只有1个解向量，线性组合基础解系 k1α1(k1≠0)。

原因是：特征向量α是非零向量，α≠O

---

注意：同一道题中，不同特征值λ对应的特征向量在线性组合时，要用k1、k2、k3…，不能只用同一个k。例如λ1对应的特征向量为k1α1(k1≠0)，λ2对应的特征向量为k2α1(k2≠0)

常见题型二：给定n阶矩阵A的所有特征值，做加减变形后得新矩阵，求新矩阵的特征值。 P254例5

步骤

1、往往用假设法，设矩阵A属于特征值-1的特征向量是α1，即Aα1= -α1

2、用新矩阵乘以该特征向量α1：B=2E-A，Bα1=(2E-A)α1=2α1-Aα1=3α1，

得到新矩阵B的特征值λ1=3

3、依次假设矩阵A属于特征值0的特征向量是α2，即Aα2= 0α2……

做题经常用到的定理：

1、矩阵对应行列式的值：|A|=特征值的乘积λ1·λ2…λn

2、矩阵A的对角线上的元素之和（矩阵的迹tr(A)）=特征值的总和λ1+λ2+…+λn

技巧：

已得到n阶矩阵A通过初等行变换化为行最简矩阵： 

(1)常规方法：

1、先找出n-r个（3-1=2）自由变量(黄色的部分)

 2、令x2=t，x3=u（t、u为任意常数）得x1-x2-x3=0即x1=t+u，x2=t，x3=u

通解X=，基础解系

(2)快捷方法：

1、先找出n-r个（3-1=2）自由变量(黄色的部分)

 2、自由变量对应的第2列和第3列先占位

 3、再把？填上，取行最简矩阵中该列的负数(从第一行往下写)

此快捷方法用有难度的题目试一下：P245例6 。快捷方法易错，可以用常规方法验证！两种方法一起使用！

---

相似矩阵

A为n阶矩阵，若存在可逆矩阵P，使P^(-1)AP=B→ 称A相似于B，B是A的相似矩阵，A~B。

若B为对角矩阵，即A的相似矩阵是对角阵→称A可相似对角化。

相似矩阵的性质：反身性A~A，对称性A~B→B~A，传递性A~B，B~C→A~C

两个n阶矩阵相似的必要条件：换句话说由两个矩阵相似A~B可以推出两个矩阵的

1、特征多项式相同  |λE-A|= |λE-B|

2、特征值相同  λ1、λ2、…、λn 

3、矩阵的秩相等  r(A)=r(B)

4、对应行列式的值相等  |A|=|B|  (= λi)  

5、矩阵的迹相等  tr(A)=tr(B)  (=λi)

矩阵相似的联想：若A~B→A^n~B^n,  A+kE~B+kE,  A^(-1)~B^(-1)

---

(矩阵A)可相似对角化的条件

定理：n阶矩阵A可相似对角化的充要条件：矩阵A有n个线性无关的特征向量。

推论：若n阶矩阵A有n个不同的特征值→ 则矩阵A可相似对角化。

且A的相似矩阵即对角矩阵为。

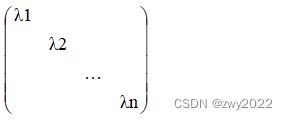
对角矩阵的主对角线上元素为特征值λ1、λ2…λn

(A可相似对角化的充分条件)

定理：n阶矩阵A可相似对角化的充要条件：(有重根时)矩阵A某个特征值的重数=该特征值对应线性无关的特征向量的个数。

（eg.A可相似对角化↔ λ1=λ2=1，矩阵A属于特征值1的-线性无关的特征向量有2个）

---

1）可逆矩阵P，使矩阵A相似对角化：P^(-1)AP=Λ（前提是n阶矩阵A可相似对角化）

2）正交矩阵Q，使实对称矩阵A相似对角化：Q^(-1)AQ=Λ

---

★★★常考题型：求可逆矩阵P 使P^(-1)AP=Λ

步骤

1、求特征值，用特征方程|λE-A|=0：求出矩阵A(设为三阶)的n个特征值 λ1、 λ2、 λ3(可以有重根)

2、求相应的特征向量，用齐次方程组的非零解(λE-A)x=0，系数矩阵A化为行最简矩阵写出基础解系：求出n个线性无关的特征向量α1、 α2、 α3

3、构造可逆矩阵P=(α1,α2,α3)，则有P^(-1)AP=Λ=

---

可逆矩阵P由n个特征向量构成。

易错点：对角矩阵Λ的主对角线上的元素(n个特征值的顺序)和可逆矩阵P中n个特征向量的顺序必须一一对应！

eg：可逆矩阵P=(α3,α1,α2)，则有P^(-1)AP=Λ=

常考题型：证明矩阵A(已知具体元素) 不可相似对角化

步骤

联想到矩阵A可相似对角化的充要条件：

(1)矩阵A有n个线性无关的特征向量

(2)(有重根时)矩阵A某个特征值的重数= 该特征值对应线性无关的特征向量的个数

---

(1)和(2)中任意一个满足，都可推出A可相似对角化

(1)和(2)中任意一个条件不成立，都可推出A不可相似对角化

---

实对称矩阵 

满足A^T=A，即aij=aji

★定理：实对称矩阵 必可相似对角化。

★定理：实对称矩阵 不同特征值的特征向量相互正交。

举例：

若λ1对应特征向量α1，λ2—α2，λ3—α3，则有α1,α2,α3相互两两正交；

有重根时，若λ1=λ2对应特征向量α1,α2，λ3—α3，则有α1和α3相互正交，α2和α3相互正交；

定理：设n阶矩阵A为实对称矩阵，必存在正交矩阵Q，使Q^(-1)AQ= Q^(T)AQ= Λ。 

因为正交矩阵Q有以下性质：Q^(T)=Q^(-1)

★★★常考题型：求正交矩阵Q 使实对称矩阵A相似对角化 Q^(-1)AQ=Λ

步骤

1、求特征值，用特征方程|λE-A|=0：求出矩阵A(设为三阶)的n个特征值 λ1、 λ2、 λ3(可以有重根)

2、求相应的特征向量，用齐次方程组的非零解(λE-A)x=0，系数矩阵A化为行最简矩阵写出基础解系：求出n个线性无关的特征向量α1、 α2、 α3​​​​​​​

3、改造特征向量​​​​​​​

①如果有n个不同的特征值，则有n个特征向量已经正交，只需要单位化，记为γ1,γ2,γ3

②如果特征值有重根，要先判断特征向量是否已经正交：

    若已经正交，只需单位化；

    若不正交，还需要正交化处理（施密特正交化P239先正交再单位化），记为γ1,γ2,γ3

4、构造正交矩阵Q=(γ1,γ2,γ3​​​​​​​)，则有Q^(-1)AQ=Λ=

---

正交矩阵Q由n个正交的单位特征向量构成。

易错点：对角矩阵Λ的主对角线上的元素(n个特征值的顺序)和正交矩阵Q中n个正交的单位特征向量的顺序必须一一对应！

eg：正交矩阵Q=(γ3,γ1,γ2​​​​​​​)，则有Q^(-1)AQ=Λ=

---

小结：相似对角化

1）可逆矩阵P，使矩阵A相似对角化：P^(-1)AP=Λ（前提是n阶矩阵A可相似对角化）

2）正交矩阵Q，使实对称矩阵A相似对角化：Q^(-1)AQ=Λ

---

★综合题型：已知矩阵A是三阶实对称矩阵，已知全部特征值为3,0,0，已知对应特征值λ=3的特征向量为α1=(1,1,1)^T

(1)求矩阵A关于特征值λ=0的特征向量

原理：实对称矩阵不同特征值的特征向量相互正交→两个向量内积为0

步骤 

1、设λ=0的特征向量为α=(x1,x2,x3)^T

2、(α1,α)=x1+x2+x3=0，解得α2=(,,)^T，α3=(,,)^T

线性组合：矩阵A关于λ=0的特征向量为k2α2+k3α3 (k2、k3不全为0)

(2)求矩阵A

原理：特征值和特征向量的定义Aα=λα

           可逆矩阵的定义A、B都是n阶矩阵，B是A的逆矩阵记为B=A^(-1)，则AB=E，BA=E

步骤

1、

2、等式两边同时乘得到A，

     

(3)求正交矩阵Q使Q^(-1)AQ=Λ

步骤

1、求n个特征值：题干已知λ1=3,λ2=λ3=0

2、求n个线性无关的特征向量：前面小题已经求得α1,α2,α3

3、改造特征向量

      首先判断特征向量是否相互正交：对λ=0，由于(α2,α3)=1≠0，特征向量α2和α3不正交，需要施密特正交化：

      ①正交化

      ②再单位化

 4、构造正交矩阵Q=(γ1,γ2,γ3​​​​​​​)，则有Q^(-1)AQ=Λ​​​​​​​

实对称矩阵A的特征值都是实数，特征向量都是实向量。