VEX —— Matrix

目录

一，矩阵相关概念

3*3 矩阵

单位矩阵保持不变

使用矩阵位移点

使用矩阵旋转点

矩阵含义

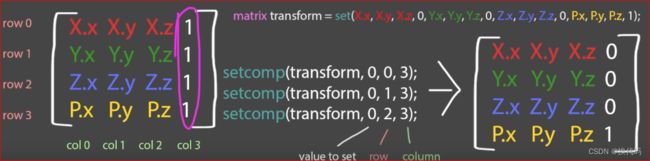
设置矩阵值 setcomp

常用矩阵相关函数

二，案例

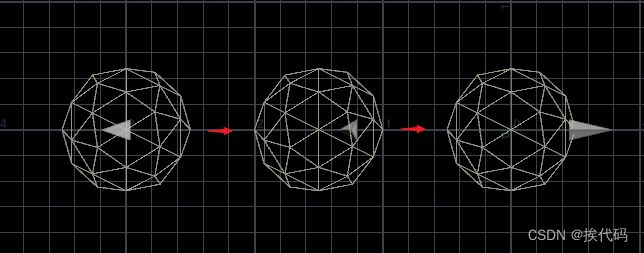
案例：源位置过渡到目标位置

---

参考 https://www.cnblogs.com/vfxJerry/p/12108565.html

一，矩阵相关概念

vex内基于row行vector，vector*matrix==matrix*vector；

向量{x, y, z, w}，w=1表示位置，w=0表示方向；

vector3 * matrix4*4, vector3自动转化为vector4(w=1)；

注，3*3矩阵和4*4矩阵之间转换需注意；

3*3 矩阵

Houdini内主要矩阵类型

• Identity Matrix
• Translation Matrix
• Rotation Matrix

单位矩阵保持不变

使用矩阵位移点

• vex函数 translate ； 

使用矩阵旋转点

• vex函数 rotate ； 

矩阵含义

设置矩阵值 setcomp

常用矩阵相关函数

ident()

translate()

rotate()

scale()

invert()

transpose()

maketransform()

cracktransform()

slerp()

instance()

lookat()

//变换
4@m=ident();
translate(@m, chv('trans'));
rotate(@m, ch('ang'),4);
scale(@m, chv('scale'));

@P *= @m;

二，案例

案例：源位置过渡到目标位置

vector P = point(1, 'P', chi('num'));
vector N = point(1, 'N', chi('num'));
matrix m1 = instance(P, N, chv('scale'));

//方法一，直接插值过渡
@P *= slerp(ident(), m1, ch('bias'));

//方法二，提取各个变换分量，分别插值过渡，最后在合并
vector t,r,s;
cracktransform(0,0,set(0,0,0),m1,t,r,s);
t = lerp(set(0,0,0),t,ch('bias'));
s = lerp(set(1,1,1),s,ch('bias'));
//旋转过渡类似 r = -lerp(set(0,0,0),r,ch('bias'));
vector4 q = eulertoquaternion(radians(r), 0);
vector4 ql = slerp(quaternion(set(0,0,0)),q,ch('bias'));
r = degrees(quaterniontoeuler(ql,0));

@P *= maketransform(0,0,t,r,s);