基于黑寡妇优化算法的函数优化算法
文章目录
- 一、理论基础
-
- 1、黑寡妇优化算法
-
- 1.1 初始化种群
- 1.2 生殖
- 1.3 同类相食
- 1.4 突变
- 1.5 更新种群
- 1.6 停止条件
- 2、BWO算法伪代码
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、黑寡妇优化算法
黑寡妇优化算法(Black Widow Optimization Algorithm, BWO)是Hayyolalam等人于2020年受黑寡妇蜘蛛独特的交配行为启发而提出的,该算法模拟了黑寡妇蜘蛛的生命周期。
BWO的每一个解(潜在解决方案)是一只黑寡妇蜘蛛,黑寡妇蜘蛛的长度等于搜索空间的维度。BWO包括初始化种群、生殖、同类相食、突变、更新种群等5个阶段,除了初始种群阶段,其他4个阶段需迭代至满足结束条件,返回适应度最佳的黑寡妇。
1.1 初始化种群
BWO中,待求解问题的一个解是一只黑寡妇蜘蛛,可以将黑寡妇蜘蛛视为一个一维数组: Widow = [ x 1 , x 2 , ⋯ , x N var ] (1) \text{Widow}=[x_1,x_2,\cdots,x_{\text{N}_\text{var}}]\tag{1} Widow=[x1,x2,⋯,xNvar](1)其中, N var \text{N}_\text{var} Nvar是优化的维度,初始化时,每个维度的值都是随机的浮点数。每只黑寡妇都有适应度,使用某个适应度函数计算黑寡妇的适应度: Fitness = f ( widow ) = f ( x 1 , x 2 , ⋯ , x N var ) (2) \text{Fitness}=f(\text{widow})=f(x_1,x_2,\cdots,x_{\text{N}_\text{var}})\tag{2} Fitness=f(widow)=f(x1,x2,⋯,xNvar)(2)初始化种群时,需要生成 N pop \text{N}_\text{pop} Npop(种群规模)只黑寡妇,得到一个 N pop × N var \text{N}_\text{pop}\times\text{N}_\text{var} Npop×Nvar的黑寡妇矩阵。
1.2 生殖
生殖阶段是全局搜索阶段。首先,根据适应度大小对种群排序,基于生殖率(procreating rate, PP)计算种群中参与生殖的黑寡妇,然后从中随机选择一对父母(雌雄黑寡妇)进行交配繁殖。在自然界中,每对黑寡妇都在自己的蜘蛛网上进行繁殖,与其他的黑寡妇是分开的,每次大约生成1000枚卵,但只有适应度较优的小蜘蛛能存活下来。在黑寡妇算法中,每对父母借助 α \alpha α数组模拟生殖过程: { y 1 = α × x 1 + ( 1 − α ) × x 2 y 2 = α × x 2 + ( 1 − α ) × x 1 (3) \begin{dcases}y_1=\alpha\times x_1+(1-\alpha) \times x_2\\[2ex]y_2=\alpha\times x_2+(1-\alpha)\times x_1\end{dcases}\tag{3} ⎩⎨⎧y1=α×x1+(1−α)×x2y2=α×x2+(1−α)×x1(3)其中, x 1 x_1 x1和 x 2 x_2 x2为父母, y 1 y_1 y1和 y 2 y_2 y2是后代。这个过程要重复 N var / 2 \text{N}_{\text{var}}/2 Nvar/2次。
1.3 同类相食
同类相食指的是适应度优的蜘蛛吃掉适应度差的蜘蛛。黑寡妇蜘蛛的同类相食分为性同类相食、兄弟姐妹同类相食和子食母同类相食三种。性同类相食是指雌黑寡妇会在交配时或交配后吃掉雄黑寡妇,可以根据适应度分辨雌雄,适应度优的为雌性,适应度差的为雄性;兄弟姐妹同类相食发生在母蛛网上,幼蛛孵化后会在母蛛网上生活一周左右,期间会发生兄弟姐妹同类相食;子食母同类相食是指某些情况下会发生小蜘蛛吃掉母蛛的事件。黑寡妇算法中,模拟了性同类相食和兄弟姐妹同类相食,子食母同类相食暂未涉及。通过摧毁父亲实现性同类相食,根据同类相食率(cannibalism rate, CR)摧毁一部分孩子达到兄弟姐妹同类相食的目的。使用适应度值确定幼蛛的强弱。
1.4 突变
突变阶段是局部搜索阶段。黑寡妇算法在这一阶段根据突变率(mutation rate, PM)随机选择多个黑寡妇,每个黑寡妇随机交换数组中的两个值。
1.5 更新种群
一次迭代之后,将同类相食阶段保留下来的黑寡妇以及突变阶段得到的黑寡妇作为下一次迭代的初始种群。
1.6 停止条件
可以考虑三种停止条件:提前设置最大迭代次数;最佳黑寡妇不再发生变化;达到预设的精度水平。
2、BWO算法伪代码
二、仿真实验与结果分析
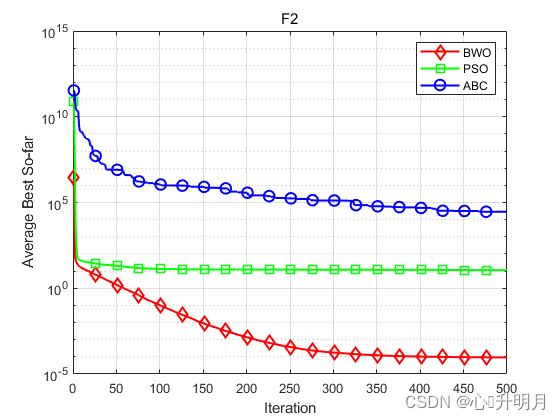
将BWO与PSO和ABC进行对比,实验设置种群规模为30,最大迭代次数为500,每个算法独立运行30次,以常用23个测试函数中的F1、F2(单峰函数/30维)、F10、F11(多峰函数/30维)、F18、F19(固定维度多峰函数/2维、3维)为例,结果显示如下:




函数:F1
BWO:最差值: 0.00030359,最优值:5.2836e-17,平均值:2.8869e-05,标准差:7.3847e-05,秩和检验:1
PSO:最差值: 209.5923,最优值:50.3202,平均值:129.6523,标准差:43.5,秩和检验:3.0199e-11
ABC:最差值: 281.5418,最优值:0.014307,平均值:48.1786,标准差:62.0608,秩和检验:3.0199e-11
函数:F2
BWO:最差值: 0.0007229,最优值:1.0132e-10,平均值:9.2838e-05,标准差:0.00017549,秩和检验:1
PSO:最差值: 19.0667,最优值:5.9133,平均值:11.3296,标准差:3.3324,秩和检验:3.0199e-11
ABC:最差值: 150645.9013,最优值:109.854,平均值:28880.8751,标准差:40205.5077,秩和检验:3.0199e-11
函数:F10
BWO:最差值: 0.031705,最优值:5.0997e-09,平均值:0.0015844,标准差:0.0057894,秩和检验:1
PSO:最差值: 7.7718,最优值:3.682,平均值:5.8866,标准差:0.9542,秩和检验:3.0199e-11
ABC:最差值: 9.5322,最优值:0.057288,平均值:4.5495,标准差:2.0996,秩和检验:3.0199e-11
函数:F11
BWO:最差值: 0.52167,最优值:6.1541e-09,平均值:0.1289,标准差:0.17456,秩和检验:1
PSO:最差值: 3.0966,最优值:1.4632,平均值:2.1382,标准差:0.42955,秩和检验:3.0199e-11
ABC:最差值: 2.5162,最优值:0.24441,平均值:1.3038,标准差:0.60401,秩和检验:2.6099e-10
函数:F18
BWO:最差值: 23.1364,最优值:3,平均值:4.1975,标准差:3.86,秩和检验:1
PSO:最差值: 3,最优值:3,平均值:3,标准差:2.7843e-15,秩和检验:2.5749e-06
ABC:最差值: 4.3362,最优值:3.0118,平均值:3.2193,标准差:0.2827,秩和检验:0.07243
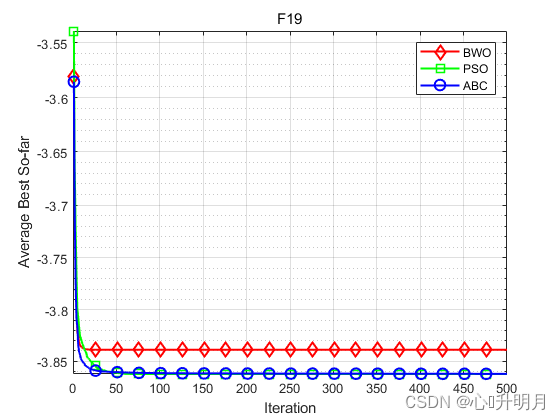
函数:F19
BWO:最差值: -3.7643,最优值:-3.8622,平均值:-3.839,标准差:0.024764,秩和检验:1
PSO:最差值: -3.8628,最优值:-3.8628,平均值:-3.8628,标准差:2.3456e-15,秩和检验:1.0598e-11
ABC:最差值: -3.8622,最优值:-3.8628,平均值:-3.8626,标准差:0.00013392,秩和检验:3.0199e-11
实验结果表明:BWO算法在寻找全局最优解时具有很高的精度和快速收敛性。
三、参考文献
[1] Vahideh Hayyolalam, Ali Asghar Pourhaji Kazem. Black Widow Optimization Algorithm: A novel meta-heuristic approach for solving engineering optimization problems[J]. Engineering Applications of Artificial Intelligence, 2020, 87: 103249.
[2] 李郅琴, 杜建强, 聂斌, 等. 基于黑寡妇算法的特征选择方法研究[J]. 计算机工程与应用, 2022, 58(16): 147-156.
