PyTorch基础（五）-- 损失函数

        在深度学习广为使用的今天，我们可以在脑海里清晰的知道，一个模型想要达到很好的效果需要学习，也就是我们常说的训练。一个好的训练离不开优质的负反馈，这里的损失函数就是模型的负反馈。

        所以在PyTorch中，损失函数是必不可少的。它是数据输入到模型当中，产生的结果与真实标签的评价指标，我们的模型可以按照损失函数的目标来做出改进。

        下面我们将开始探索pytorch的所拥有的损失函数。这里将列出PyTorch中常用的损失函数（一般通过torch.nn调用），并详细介绍每个损失函数的功能介绍、数学公式和调用代码。当然，PyTorch的损失函数还远不止这些，在解决实际问题的过程中需要进一步探索、借鉴现有工作，或者设计自己的损失函数。

1.1 二分类交叉熵损失函数

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

        功能：计算二分类任务时的交叉熵（Cross Entropy）函数。在二分类中，label是{0,1}。对于进入交叉熵函数的input为概率分布的形式。一般来说，input为sigmoid激活层的输出，或者softmax的输出。

主要参数：

• weight:每个类别的loss设置权值
• size_average:数据为bool，为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
• reduce:数据类型为bool，为True时，loss的返回是标量。

        计算公式如下：
$$\ell (x,y)=\{\begin{array}{ll}\mathrm{mean}(L),& \text{ if reduction }=\text{ ’mean’ }\\ \mathrm{sum}(L),& \text{ if reduction }=\text{ ’sum’ }\end{array}$$

m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(m(input), target)
output.backward()

print('BCELoss损失函数的计算结果为',output)

BCELoss损失函数的计算结果为 tensor(0.5732, grad_fn=)

1.2 交叉熵损失函数

torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

功能：计算交叉熵函数

主要参数：

• weight:每个类别的loss设置权值。
• size_average:数据为bool，为True时，返回的loss为平均值；为False时，返回的各样本的loss之和。
• ignore_index:忽略某个类的损失函数。
• reduce:数据类型为bool，为True时，loss的返回是标量。

        计算公式如下：
$$\mathrm{loss}(x,\text{ class })=-\log \left(\frac{\exp (x[\text{ class }])}{{\sum }_j\exp (x[j])}\right)=-x[\text{ class }]+\log \left(\sum _j\exp (x[j])\right)$$

loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()

print(output)

  tensor(2.0115, grad_fn=)

1.3 L1损失函数

torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')

功能： 计算输出y和真实标签target之间的差值的绝对值。

        我们需要知道的是，reduction参数决定了计算模式。有三种计算模式可选：

• none：逐个元素计算。
• sum：所有元素求和，返回标量。
• mean：加权平均，返回标量。

        如果选择none，那么返回的结果是和输入元素相同尺寸的。默认计算方式是求平均。

计算公式如下：
$$L_n=|x_n-y_n|$$

loss = nn.L1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

print('L1损失函数的计算结果为',output)

 L1损失函数的计算结果为 tensor(1.5729, grad_fn=)

1.4 MSE损失函数

torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')

功能： 计算输出y和真实标签target之差的平方。

        和L1Loss一样，MSELoss损失函数中，reduction参数决定了计算模式。有三种计算模式可选：none：逐个元素计算。
sum：所有元素求和，返回标量。默认计算方式是求平均。

计算公式如下：

$$l_n={\left(x_n-y_n\right)}^2$$

loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

print('MSE损失函数的计算结果为',output)

MSE损失函数的计算结果为 tensor(1.6968, grad_fn=)

1.5 平滑L1 (Smooth L1)损失函数

torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction='mean', beta=1.0)

功能： L1的平滑输出，其功能是减轻离群点带来的影响

        reduction参数决定了计算模式。有三种计算模式可选：none：逐个元素计算。sum：所有元素求和，返回标量。默认计算方式是求平均。

提醒： 之后的损失函数中，关于reduction 这个参数依旧会存在。所以，之后就不再单独说明。

计算公式如下：
$$\mathrm{loss}(x,y)=\frac{1}{n}\sum _{i=1}^n{z}_i$$
其中，
$$z_i=\{\begin{array}{ll}0.5{\left(x_i-y_i\right)}^2,& \text{ if }\left|x_i-y_i\right|<1\\ \left|x_i-y_i\right|-0.5,& \text{ otherwise }\end{array}$$

loss = nn.SmoothL1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

print('SmoothL1Loss损失函数的计算结果为',output)

SmoothL1Loss损失函数的计算结果为 tensor(0.7808, grad_fn=)

平滑L1与L1的对比

        这里我们通过可视化两种损失函数曲线来对比平滑L1和L1两种损失函数的区别。

inputs = torch.linspace(-10, 10, steps=5000)
target = torch.zeros_like(inputs)

loss_f_smooth = nn.SmoothL1Loss(reduction='none')
loss_smooth = loss_f_smooth(inputs, target)
loss_f_l1 = nn.L1Loss(reduction='none')
loss_l1 = loss_f_l1(inputs,target)

plt.plot(inputs.numpy(), loss_smooth.numpy(), label='Smooth L1 Loss')
plt.plot(inputs.numpy(), loss_l1, label='L1 loss')
plt.xlabel('x_i - y_i')
plt.ylabel('loss value')
plt.legend()
plt.grid()
plt.show()

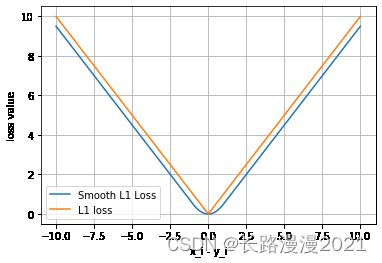
        可以看出，对于smoothL1来说，在 0 这个尖端处，过渡更为平滑。

1.6 目标泊松分布的负对数似然损失

torch.nn.PoissonNLLLoss(log_input=True, full=False, size_average=None, eps=1e-08, reduce=None, reduction='mean')

功能： 泊松分布的负对数似然损失函数

主要参数：

• log_input：输入是否为对数形式，决定计算公式。
• full：计算所有 loss，默认为 False。
• eps：修正项，避免 input 为 0 时，log(input) 为 nan 的情况。

数学公式：

• 当参数log_input=True：
  $$\mathrm{loss}\left(x_n,y_n\right)=e^{x_n}-x_n\cdot y_n$$

• 当参数log_input=False：

  $$\mathrm{loss}\left(x_n,y_n\right)=x_n-y_n\cdot \log \left(x_n+\text{ eps }\right)$$

loss = nn.PoissonNLLLoss()
log_input = torch.randn(5, 2, requires_grad=True)
target = torch.randn(5, 2)
output = loss(log_input, target)
output.backward()

print('PoissonNLLLoss损失函数的计算结果为',output)

PoissonNLLLoss损失函数的计算结果为 tensor(0.7358, grad_fn=)

1.7 KL散度

torch.nn.KLDivLoss(size_average=None, reduce=None, reduction='mean', log_target=False)

功能： 计算KL散度，也就是计算相对熵。用于连续分布的距离度量，并且对离散采用的连续输出空间分布进行回归通常很有用。

主要参数:

reduction：计算模式，可为 none/sum/mean/batchmean。

• none：逐个元素计算。
• sum：所有元素求和，返回标量。
• mean：加权平均，返回标量。
• batchmean：batchsize 维度求平均值。

计算公式：

$$\begin{array}{rl}{D}_{\mathrm{K}\mathrm{L}}(P,Q)={\mathrm{E}}_{X\sim P}\left[\log \frac{P(X)}{Q(X)}\right]& ={\mathrm{E}}_{X\sim P}[\log P(X)-\log Q(X)]\\ & =\sum _{i=1}^{n}P\left(x_i\right)\left(\log P\left(x_i\right)-\log Q\left(x_i\right)\right)\end{array}$$

inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)
loss = nn.KLDivLoss()
output = loss(inputs,target)

print('KLDivLoss损失函数的计算结果为',output)

KLDivLoss损失函数的计算结果为 tensor(-0.3335)

1.8 MarginRankingLoss

torch.nn.MarginRankingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

功能： 计算两个向量之间的相似度，用于排序任务。该方法用于计算两组数据之间的差异。

主要参数:

• margin：边界值，$x_1$ 与$x_2$ 之间的差异值。
• reduction：计算模式，可为 none/sum/mean。

计算公式：

$$\mathrm{loss}(x1,x2,y)=\max (0,-y\ast (x1-x2)+\mathrm{margin})$$

loss = nn.MarginRankingLoss()
input1 = torch.randn(3, requires_grad=True)
input2 = torch.randn(3, requires_grad=True)
target = torch.randn(3).sign()
output = loss(input1, input2, target)
output.backward()

print('MarginRankingLoss损失函数的计算结果为',output)

MarginRankingLoss损失函数的计算结果为 tensor(0.7740, grad_fn=)

1.9 多标签边界损失函数

torch.nn.MultiLabelMarginLoss(size_average=None, reduce=None, reduction='mean')

功能： 对于多标签分类问题计算损失函数。

主要参数:

• reduction：计算模式，可为 none/sum/mean。

计算公式：
$$\begin{gathered} \mathrm{loss}(x,y)=\sum _{ij}\frac{\max (0,1-x[y[j]]-x[i])}{x\cdot \mathrm{size}(0)} \\ \begin{array}{l}\text{ 其中, }i=0,\dots ,x\cdot \mathrm{size}(0),j=0,\dots ,y\cdot \mathrm{size}(0),\text{ 对于所有的 }i\text{ 和 }j\text{, 都有 }y[j]\ge 0\text{ 并且 }\\ i\ne y[j]\end{array} \end{gathered}$$

loss = nn.MultiLabelMarginLoss()
x = torch.FloatTensor([[0.9, 0.2, 0.4, 0.8]])
# for target y, only consider labels 3 and 0, not after label -1
y = torch.LongTensor([[3, 0, -1, 1]])# 真实的分类是，第3类和第0类
output = loss(x, y)

print('MultiLabelMarginLoss损失函数的计算结果为',output)

MultiLabelMarginLoss损失函数的计算结果为 tensor(0.4500)

1.10 二分类损失函数

torch.nn.SoftMarginLoss(size_average=None, reduce=None, reduction='mean')torch.nn.(size_average=None, reduce=None, reduction='mean')

功能： 计算二分类的 logistic 损失。

主要参数:

• reduction：计算模式，可为 none/sum/mean。

计算公式：

$$\begin{gathered} \mathrm{loss}(x,y)=\sum _i\frac{\log (1+\exp (-y[i]\cdot x[i]))}{x\cdot \mathrm{nelement}()} \\ \text{ 其中, }x.\text{ nelement() 为输入 }x\text{ 中的样本个数。注意这里 }y\text{ 也有 }1\text{ 和 }-1\text{ 两种模式。 } \end{gathered}$$

inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])  # 两个样本，两个神经元
target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)  # 该 loss 为逐个神经元计算，需要为每个神经元单独设置标签

loss_f = nn.SoftMarginLoss()
output = loss_f(inputs, target)

print('SoftMarginLoss损失函数的计算结果为',output)

SoftMarginLoss损失函数的计算结果为 tensor(0.6764)

1.11 多分类的折页损失

torch.nn.MultiMarginLoss(p=1, margin=1.0, weight=None, size_average=None, reduce=None, reduction='mean')

功能： 计算多分类的折页损失

主要参数:

• reduction：计算模式，可为 none/sum/mean。
• p：可选 1 或 2。
• weight：各类别的 loss 设置权值。
• margin：边界值

计算公式：

$$\begin{gathered} \mathrm{loss}(x,y)=\frac{{\sum }_i\max (0,\mathrm{margin}-x[y]+x[i]{)}^p}{x\cdot \mathrm{size}(0)} \\ \begin{array}{l}\text{ 其中, }x\in \{0,\dots ,x\cdot \mathrm{size}(0)-1\},y\in \{0,\dots ,y\cdot \mathrm{size}(0)-1\}\text{, 并且对于所有的 }i\text{ 和 }j\text{, }\\ \text{ 都有 }0\le y[j]\le x\cdot \mathrm{size}(0)-1,\text{ 以及 }i\ne y[j]\text{ 。 }\end{array} \end{gathered}$$

inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]]) 
target = torch.tensor([0, 1], dtype=torch.long) 

loss_f = nn.MultiMarginLoss()
output = loss_f(inputs, target)

print('MultiMarginLoss损失函数的计算结果为',output)

MultiMarginLoss损失函数的计算结果为 tensor(0.6000)

1.12 三元组损失

torch.nn.TripletMarginLoss(margin=1.0, p=2.0, eps=1e-06, swap=False, size_average=None, reduce=None, reduction='mean')

功能： 计算三元组损失。

三元组: 这是一种数据的存储或者使用格式。<实体1，关系，实体2>。在项目中，也可以表示为< anchor, positive examples , negative examples>

在这个损失函数中，我们希望去anchor的距离更接近positive examples，而远离negative examples

主要参数:

• reduction：计算模式，可为 none/sum/mean。
• p：可选 1 或 2。
• margin：边界值

计算公式：
$$\begin{gathered} L(a,p,n)=\max \left\{d\left(a_i,p_i\right)-d\left(a_i,n_i\right)+\mathrm{margin},0\right\} \\ \text{ 其中, }d\left(x_i,y_i\right)={\Vert {\mathbf{x}}_i-{\mathbf{y}}_i\Vert }_{\text{・ }} \end{gathered}$$

triplet_loss = nn.TripletMarginLoss(margin=1.0, p=2)
anchor = torch.randn(100, 128, requires_grad=True)
positive = torch.randn(100, 128, requires_grad=True)
negative = torch.randn(100, 128, requires_grad=True)
output = triplet_loss(anchor, positive, negative)
output.backward()
print('TripletMarginLoss损失函数的计算结果为',output)

TripletMarginLoss损失函数的计算结果为 tensor(1.1667, grad_fn=)

1.13 HingEmbeddingLoss

torch.nn.HingeEmbeddingLoss(margin=1.0, size_average=None, reduce=None, reduction='mean')

功能： 对输出的embedding结果做Hing损失计算

主要参数:

• reduction：计算模式，可为 none/sum/mean。
• margin：边界值

计算公式：
$$l_n=\{\begin{array}{ll}{x}_n,& \text{ if }{y}_n=1\\ \max \left\{0,\Delta -x_n\right\},& \text{ if }{y}_n=-1\end{array}$$
注意事项： 输入x应为两个输入之差的绝对值。

        可以这样理解，让个输出的是正例yn=1,那么loss就是x，如果输出的是负例y=-1，那么输出的loss就是要做一个比较。

loss_f = nn.HingeEmbeddingLoss()
inputs = torch.tensor([[1., 0.8, 0.5]])
target = torch.tensor([[1, 1, -1]])
output = loss_f(inputs,target)

print('HingEmbeddingLoss损失函数的计算结果为',output)

HingEmbeddingLoss损失函数的计算结果为 tensor(0.7667)

1.14 余弦相似度

torch.nn.CosineEmbeddingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

功能： 对两个向量做余弦相似度

主要参数:

• reduction：计算模式，可为 none/sum/mean。
• margin：可取值[-1,1] ，推荐为[0,0.5] 。

计算公式：

$$\mathrm{loss}(x,y)=\{\begin{array}{ll}1-\cos \left(x_1,x_2\right),& \text{ if }y=1\\ \max \left\{0,\cos \left(x_1,x_2\right)-\text{ margin }\right\},& \text{ if }y=-1\end{array}$$
其中,
$$\cos (\theta )=\frac{A\cdot B}{\Vert A\Vert \Vert B\Vert }=\frac{{\sum }_{i=1}^n{A}_i\times B_i}{\sqrt{{\sum }_{i=1}^n{\left(A_i\right)}^2}\times \sqrt{{\sum }_{i=1}^n{\left(B_i\right)}^2}}$$

        这个损失函数应该是最广为人知的。对于两个向量，做余弦相似度。将余弦相似度作为一个距离的计算方式，如果两个向量的距离近，则损失函数值小，反之亦然。

loss_f = nn.CosineEmbeddingLoss()
inputs_1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]])
inputs_2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]])
target = torch.tensor([[1, -1]], dtype=torch.float)
output = loss_f(inputs_1,inputs_2,target)

print('CosineEmbeddingLoss损失函数的计算结果为',output)

CosineEmbeddingLoss损失函数的计算结果为 tensor(0.5000)

1.15 CTC损失函数

torch.nn.CTCLoss(blank=0, reduction='mean', zero_infinity=False)

功能： 用于解决时序类数据的分类

        计算连续时间序列和目标序列之间的损失。CTCLoss对输入和目标的可能排列的概率进行求和，产生一个损失值，这个损失值对每个输入节点来说是可分的。输入与目标的对齐方式被假定为 “多对一”，这就限制了目标序列的长度，使其必须是≤输入长度。

主要参数:

• reduction：计算模式，可为 none/sum/mean。
• blank：blank label。
• zero_infinity：无穷大的值或梯度值为

# Target are to be padded
T = 50      # Input sequence length
C = 20      # Number of classes (including blank)
N = 16      # Batch size
S = 30      # Target sequence length of longest target in batch (padding length)
S_min = 10  # Minimum target length, for demonstration purposes

# Initialize random batch of input vectors, for *size = (T,N,C)
input = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()

# Initialize random batch of targets (0 = blank, 1:C = classes)
target = torch.randint(low=1, high=C, size=(N, S), dtype=torch.long)

input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.randint(low=S_min, high=S, size=(N,), dtype=torch.long)
ctc_loss = nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
loss.backward()


# Target are to be un-padded
T = 50      # Input sequence length
C = 20      # Number of classes (including blank)
N = 16      # Batch size

# Initialize random batch of input vectors, for *size = (T,N,C)
input = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()
input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)

# Initialize random batch of targets (0 = blank, 1:C = classes)
target_lengths = torch.randint(low=1, high=T, size=(N,), dtype=torch.long)
target = torch.randint(low=1, high=C, size=(sum(target_lengths),), dtype=torch.long)
ctc_loss = nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
loss.backward()

print('CTCLoss损失函数的计算结果为',loss)

CTCLoss损失函数的计算结果为 tensor(16.0885, grad_fn=)