数据挖掘课后作业

数据挖掘课后作业

第一章

一.单选题*（共4题,40.0分）*

1. 下列选项哪个描述的是“训练样本” B

• A、在电子病历数据中，每一个样本有八个检测指标，但是没有医生诊断结果
• B、在电子病历数据中，每一个样本有八个检测指标，每个样本还有一个医生诊断结果
• C、在电子病历数据中，每一个样本有八个检测指标，但是没有医生诊断结果；算法自动得到这些样本的诊断结果
• D、在电子病历数据中，每一个样本有八个检测指标，医生根据这八个指标做出诊断

2下列选项哪个描述的是“分类”C

• A、在电子病历数据中，每一个样本有八个检测指标，但是没有医生诊断结果
• B、在电子病历数据中，每一个样本有八个检测指标，每个样本还有一个医生诊断结果
• C、在电子病历数据中，每一个样本有八个检测指标，但是没有医生诊断结果；算法自动得到这些样本的诊断结果
• D、在电子病历数据中，每一个样本有八个检测指标，医生根据这八个指标做出诊断

​

3下列哪个选项描述的不是“聚类” C

• A、搜索引擎返回的文档中，将相似的文档聚合成一类
• B、电子商务网站数据中，购物历史相似的用户自动聚合成一组
• C、电子商务网站数据中，分析出用户常常一起购买的商品，组合到一起促销
• D、在电子病历数据中，将体检指标相似的样本自动聚合成一组

​

4在MATLAB语言中，以下说法中错误的是（C）

• A、MATLAB中默认的数据类型是double
• B、3<5的运算结果是logical类型
• C、变量Abc和abc是代表两个相同的变量
• D、灰度图的图像矩阵中的数据是uint8类型

二.多选题*（共3题,30.0分）*

1引发人们对数据挖掘开展研究的挑战性问题包括（ABCDE ） ：

• A、可伸缩
• B、高维性
• C、异种数据和复杂数据
• D、数据的所有权与分布
• E、非传统的分析

​

2下列哪些属于预测性任务（BC ）

• A、关联规则发现

• B、分类

• C、回归

• D、聚类

  

​

3下列哪些属于描述性任务AD

• A、关联规则发现
• B、分类
• C、回归
• D、聚类

​

三.填空题*（共3题,30.0分）*

1执行完matlab命令“a=[1, 2; 2, 3; 6, 10]”之后，a中的数据有3 行 2列

2执行完matlab命令“a=[2:3:10]”之后，a中的数据依次为 2 、5 、 8

3执行完matlab命令“a=[1, 2; 4, 3; 6, 10]”之后，a(3,2)的值为 10

​

第二章

一.单选题*（共6题,60.0分）*

1数据对象的别名不包括： D

• A、记录
• B、样本
• C、向量
• D、特征

​

2属性的别名不包括： B

• A、特征

• B、样本

• C、字段

• D、维

3下列说法不正确的是 C

• A、测量标度是将数值或符号与对象的属性相关联的规则

• B、属性的性质不必与用来度量它的值的性质完全相同

• C、即使在不同的应用问题中，同一个物理量也必然使用同一种类型的属性来描述

• D、属性类型可以划分为：标称、序数、区间、比率这四种

4某办公自动化系统中，采用出生年份表示雇员的年龄，这是什么类型属性 C

• A、标称
• B、序数
• C、区间
• D、比率

5某学籍管理系统中，采用百分制表示学生分数，这是什么类型属性 D

​

• A、标称
• B、序数
• C、区间
• D、比率

​

6描述一个数据集的属性主要不包括： A

• A、置信度
• B、维度
• C、分辨率
• D、稀疏性

二.填空题*（共4题,40.0分）*

1执行完matlab命令X=[3 2 0; -5 6 1]; indices =find(X>=1) 之后，变量indices中的值依次是 1、 3 、4 、 6

​

2已知X=[3 2 0 4; -5 6 1 2]; 执行完matlab命令“X(:,2)=[ ]”之后，X矩阵有2行3 列**

​

3分析以下matlab命令的执行结果：

x=[3,2,1,0]

a=length(x)

b=size(x,1)

c=size(x,2)

s=sum(x)

a的值为 4

b的值为 1

c的值为 4

s的值为 6

​

4已知函数定义如下，

function [y]=fun(x)

if(x<-5)

  y=x*3;

elseif(x<=0)

  y=-x;

else

  y=x*2;

end

end

fun(-10)的返回值为 -30

fun(-5)的返回值为 5

fun(3)的返回值为 6

​

第三次

一.单选题*（共3题,30.0分）*

1下列说法中错误的是：（10.0分） D

• A、噪声是测量误差的随机部分
• B、数据中出现遗漏值的原因，可能是信息没有收集到，或者属性不适用于所有情况。
• C、通常由于不同的数据源合并时造成重复数据的产生
• D、离群点不可能是合法的数据对象或值

!

2下列选项中不属于数据预处理方法的是（10.0分） B

• A、维归约
• B、聚类
• C、离散化与二元化
• D、属性变换

3下列说法中错误的是：（10.0分） B

• A、维归约是通过创建新属性，将一些旧属性合并在一起来降低数据集的维度值
• B、通过聚集操作，对象或属性群的行为通常比单个对象或属性的行为更加稳定；并且聚集操作不会丢失有趣的细节
• C、之所以可以进行特征子集选择，是因为特征中通常包含冗余特征和不相关特征
• D、特征创建方法包括：特征提取、映射数据到新的空间、特征构造

​

二.填空题*（共1题,20.0分）*

1向量x=[3,2,3,1],y=[1,4,5,3],两者之间的欧几里得距离为 （20.0分） 4；根号16

​

三.判断题*（共5题,50.0分）*

1通常，信用卡盗刷的交易记录在全体信用卡交易的事务数据中，可以视为是离群点。 √

​

2离群点可以是合法的数据对象或值。 （10.0分） √

​

​

3数据中出现遗漏值的原因，可能是信息没有收集到，或者属性不适用于所有情况。 √

​

4维归约和特征子集选择这两种操作都可以达到降低数据维度的效果。 √

5对变量进行标准化/规范化，就是创建一个新的变量，它具有均值0和标准差0 ×

第四次

一.填空题*（共6题,100.0分）*

1、x=[1,2,0,2,0],y=[2,2,2,0,2],两者之间的夹角余弦相似度为 1/2；0.5；

2、x=[1,3,0,2],y=[2,3,2,0],两者之间的欧几里得距离为 3；根号9

3、x=[0,1,1,0,0],y=[1,1,0,0,1],两者之间的Jaccard相似性系数为 1/4；0.25

​ x=[0,1,1,0,0]

​ y=[1,1,0,0,1]

4、x=[0,1,1,0,0],y=[1,1,0,0,1],两者之间的简单匹配系数为 2/5；0.4

x=[0,1,1,0,0],

y=[1,1,0,0,1]

​

5

已知有5个训练样本，分别为

样本1，属性为：[2,0,2] 类别 0

样本2，属性为：[1,5,2] 类别 1

样本3，属性为：[3,2,3] 类别 1

样本4，属性为：[3,0,2] 类别 0

样本5，属性为：[1,0,6] 类别 0

有1个测试样本，属性为：[1,0,2]

1、测试样本到5个训练样本（样本1、2、3、4、5）的欧氏距离依次为： 1 、5 、3 、2 、 4

2、K=3，距离测试样本最近的k个训练样本依次为：样本 1 、样本 4、样本 3

3、距离最近的k个训练样本类别依次为：类别 0 、类别 0、类别 1

4、KNN算法得到的测试样本的类别为：类别 0

第五次

一.填空题*（共7题,100.0分）*

1数据的属性已知，数据的类别也已知，这样的数据叫做 训练 样本

2数据的属性已知，数据的类别未知，这样的数据叫做 测试 样本

3

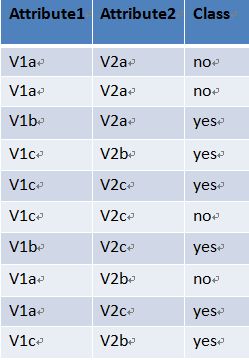
已知训练数据集如表1：该数据集中，P(yes)= 0.6 P(no)= 0.4

该数据集的熵为 Info(D) = I(6,4)

（说明：熵可以写成I(m,n)的形式，或者写成-(b/a)*log2(b/a) -( d/c)*log2(d/c)的形式 其中，分数b/a、d/c约分为最简形式）

（30.0分）

​

​ 第一空： 6/10；3/5；

第二空： 4/10；2/5；

第三空： I(6,4)；–(3/5)log2(3/5)–(2/5)log2(2/5)；–(3/5)*log2(3/5)–(2/5)*log2(2/5)；–(2/5)log2(2/5)–(3/5)log2(3/5)；–(2/5)*log2(2/5)–(3/5)*log2(3/5)

4接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。三个子集的样本数量与原始数据集的比例分别为 、 、

（15.0分）

​

[正确答案：](javascript:void(0))

第一空： 4/10；2/5；0.4

​ 第二空： 2/10；1/5；0.2

​ 第三空： 4/10；2/5；0.4

5接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。三个子集的熵分别为 、 、

（说明：熵可以写成I(m,n)的形式，或者写成-(b/a)*log2(b/a) -( d/c)*log2(d/c)的形式 其中，分数b/a、d/c约分为最简形式）

（30.0分）

[正确答案：](javascript:void(0))

第一空： I(1,3)；I(3,1)； – (1/4)log2(1/4)–(3/4)log2(3/4)；–(1/4)*log2(1/4)–(3/4)*log2(3/4)； – (3/4)log2(3/4)–(1/4)log2(1/4)；–(3/4)*log2(3/4)–(1/4)log2(1/4) 第二空： I(2,0)；I(0,2)；– 1log2(1)；– 1log2(1)；0 第三空： I(1,3)；I(3,1)； – (1/4)log2(1/4)–(3/4)log2(3/4)；–(1/4)*log2(1/4)–(3/4)*log2(3/4)； – (3/4)log2(3/4)–(1/4)log2(1/4)；–(3/4)*log2(3/4)–(1/4)*log2(1/4)

6接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。该划分的期望信息为

（答案写成 (b/a) I(m,n)+(d/c) I(m,n) 的形式 。其中，分数b/a、d/c约分为最简形式）

（10.0分）

​

第一空： (2/5)*I(1,3)+(1/5)*I(2,0)+(2/5)*I(3,1)；(4/5)*I(1,3)+(1/5)*I(2,0)；(4/5)*I(3,1)+(1/5)*I(2,0)；(1/5)*I(2,0)+(4/5)*I(3,1)；(1/5)*I(2,0)+(4/5)*I(1,3)；(4/5)*I(1,3)；(4/5)*I(3,1)；(2/5)*I(1,3)+(2/5)*I(3,1)；(2/5)*I(3,1)+(2/5)*I(1,3)

7接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。该划分的信息增益为

（信息增益用包含 I(m,n)的式子表示 ）

（10.0分）

​

​ 第一空： I(6,4)-((2/5)*I(1,3)+(1/5)*I(2,0)+(2/5)*I(3,1))；I(6,4)-(2/5)*I(1,3)-(1/5)*I(2,0)-(2/5)*I(3,1)；I(6,4)-((4/5)*I(1,3)+(1/5)*I(2,0))；I(6,4)-(4/5)*I(1,3)-(1/5)*I(2,0)；I(6,4)-((4/5)*I(3,1)+(1/5)*I(2,0))；I(6,4)-(4/5)*I(3,1)-(1/5)*I(2,0)；I(6,4)-((1/5)*I(2,0)+(4/5)*I(3,1))；I(6,4)-(1/5)*I(2,0)-(4/5)*I(3,1)；I(6,4)-((1/5)*I(2,0)+(4/5)*I(1,3))；I(6,4)-(1/5)*I(2,0)-(4/5)*I(1,3)

​

第六次

一.填空题*（共3题,37.5分）*

1已知一个数据集，其中有2个类的样本，这2个类的样本数量分别为1、2，则该数据集的熵值为

–(1/3)log2(1/3)–(2/3)log2(2/3)

（说明：熵写成-(b/a)*log2(b/a)-(d/c)*log2(d/c)的形式。其中，分数b/a、d/c约分为最简形式）

第一空： –(1/3)log2(1/3)–(2/3)log2(2/3)；–(2/3)log2(2/3)–(1/3)log2(1/3)；-(1/3)log2(1/3)-(2/3)log2(2/3)；-(2/3)log2(2/3)-(1/3)log2(1/3)

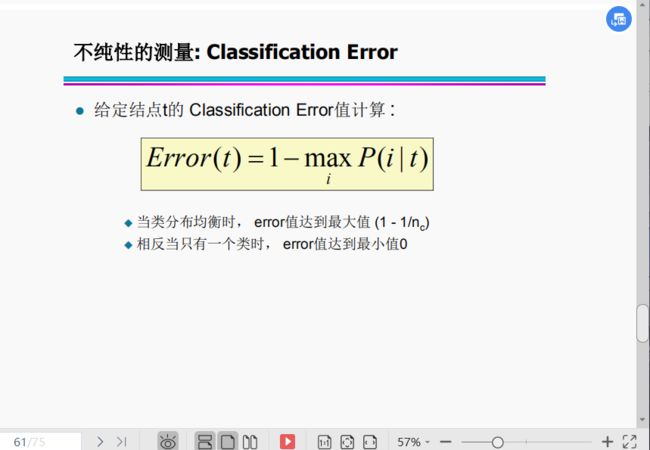
2已知一个数据集，其中有3个类的样本，这3个类的样本数量分别为1、1、3，则该数据集的Classification Error为 0.4（结果用小数或分数表示）

​

第一空： 2/5；0.4；0.40

3

已知一个数据集，其中有2个类的样本，这2个类的样本数量分别为1、4，则该数据集的GINI值为 0.32 （结果用小数或分数表示，小数保留小数点后2位）

​

第一空： 8/25；0.32

二.判断题*（共5题,62.5分）*

1训练误差，是分类模型在训练记录上误分类样本的比例；泛化误差，是分类模型在未知的测试记录上的期望误差 √

2出现拟合不足的原因是模型尚未学习到数据的真实结构 √

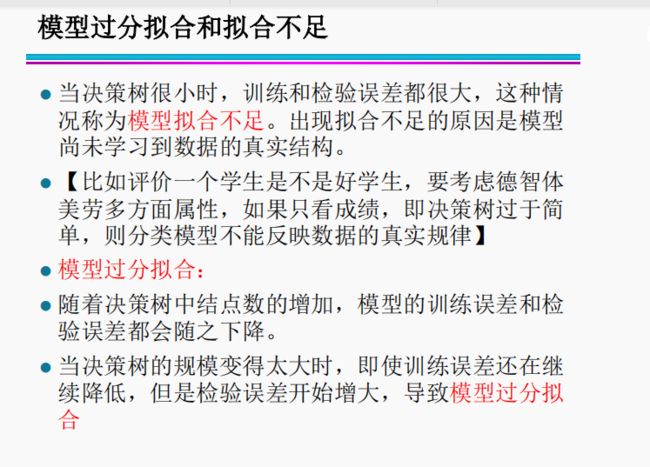
3当决策树很小时，训练和检验误差都很大，这种情况称为模型过分拟合 ×

4当决策树的规模变得太大时，即使训练误差还在继续降低，但是检验误差开始增大，导致模型拟合不足

​ ×

5导致过分拟合的原因包括：训练数据中存在噪声、训练数据中缺乏代表性样本 √

第七次

一.填空题*（共4题,100.0分）*

1

已知训练数据集如表1：

该数据集中，分类为“yes”“no”的先验概率各自是多少？

P(yes)= 0.6

P(no)= 0.4

第一空： 6/10；3/5；0.6

​ 第二空： 4/10；2/5；0.4

2接上题，已知训练数据集如表1。已知待分类的测试样本X=（Attribute1= V1c, Attribute2= V2c）

计算以下条件概率：（答案请表示为分数b/a；b/a约分为最简形式）

P(Attribute1= V1c |yes)= 1/2

P(Attribute1= V1c |no)= 1/4

P(Attribute2= V2c |yes)= 1/2

P(Attribute2= V2c |no)= 1/4

P(Attribute1= V1c, Attribute2= V2c |yes)= 1/4

P(Attribute1= V1c, Attribute2= V2c |no)= 1/16

（60.0分）

​

​ 第一空： 1/2

第二空： 1/4

第三空： 1/2

​ 第四空： 1/4

​ 第五空： 1/4

​ 第六空： 1/16

3接上题，已知训练数据集如表1。已知待分类的测试样本X=（Attribute1= V1c, Attribute2= V2c）。

后验概率P(no|X)、P(yes|X) 各自是多少？（答案请表示为分数b/a；b/a约分为最简形式）

P(yes | Attribute1= V1c, Attribute2= V2c)= 3/20 （说明：忽略分母1/P(X)）

P(no| Attribute1= V1c, Attribute2= V2c)= 1/40 （说明：忽略分母1/P(X)）

​ 第一空： 3/20

第二空： 1/40

4接上题，已知训练数据集如表1。已知待分类的测试样本X=（Attribute1= V1c, Attribute2= V2c）。

该测试样本被分成哪一类？A

A yes

B no

请填写A或B

​

第八次

一.判断题*（共10题,100.0分）*

1**线性支持向量机是基于“****最大边缘”**原理，即希望实现分类器边缘最大化。 √

2线性支持向量机，在求解分类器边缘最大化的过程中，不需要满足将两类训练样本正确分开的前提

​ ×

3实现分类器边缘最大化，可以使得新的测试数据被错分的几率尽可能小，从而使得分类器的泛化能力最大化。 √

4线性支持向量机的求解是一个凸二次优化问题，不能保证找到全局最优解。 ×

5对存在数据污染、近似线性分类的情况, 要求分类器将所有训练数据都准确分类，不会导致过拟合。

​ ×

6对存在数据污染、近似线性分类的情况,可以使用软边缘支持向量机。 √

7软间隔支持向量机通过引入松弛变量、惩罚因子，在一定程度上允许错误分类样本，以增大间隔距离。在分类准确性与泛化能力上寻求一个平衡点。 √

8对非线性可分的问题，可以利用核变换，把原样本映射到某个高维特征空间，使得原本在低维特征空间中非线性可分的样本，在新的高维特征空间中变得线性可分。 √

9软间隔支持向量机的求解，可以证找到全局最优解。非线性支持向量机的求解，可以证找到全局最优解。

​ √

10支持向量机的工作原理决定了，该算法只能解决二分问题，不能解决多类分类问题。

​ ×

第九次

一.填空题*（共8题,100.0分）*

1在神经元细胞中，树突 是接受从其它神经元传入的信息的入口。

​

2在神经元细胞中， 轴突 是把神经元兴奋的信息传出到其它神经元的出口。

​

3感知器模型的输出可以用此公式计算： Y=sign(0.3x1+0.3x2+0.3x3-0.4)。若输入x1= 1，x2= 0，x3= 1，输出 Ｙ＝ 1

4多层人工神经网络包括： 输入 层、 隐藏 层、输出 层

5梯度下降算法中，当学习率设置得过 小 时，收敛过程将变得十分缓慢。

6梯度下降算法中，当学习率设置的过 大时，梯度可能会在最小值附近来回震荡，甚至可能无法收敛

7logistic回归问题中的损失函数L(a,y)=-(yln(a)+(1-y)ln(1-a))，说明：a为样本类别为1的概率估计，y为样本的真实类别。当y=0，损失函数的单调性是 A
Ａ．单调递增　　　Ｂ．单调递减　　　Ｃ　非单调

8logistic回归问题中的损失函数L(a,y)=-(yln(a)+(1-y)ln(1-a))，说明：a为样本类别为1的概率估计，y为样本的真实类别。当y=1**，损失函数的单调性是** B

Ａ．单调递增　　　Ｂ．单调递减　　　Ｃ　非单调

​

第十次

一.填空题*（共2题,40.0分）*

1已知某个二类分类问题的混淆矩阵数据如下：TP=90 , FN=20 , TN=120 , FP=10 ，则计算其召回率为**9/11 **（答案请表示为分数b/a；b/a约分为最简形式）

2已知某个二类分类问题的混淆矩阵数据如下：TP=90 , FN=20 , TN=120 , FP=10 ，则计算其精度为 9/10 （答案请表示为分数b/a；b/a约分为最简形式）

二.判断题*（共3题,60.0分）*

1ROC曲线下方的面积AUC越大，说明分类器性能越好 √

2ROC曲线的纵轴是真正率，横轴是假正率 √

3、6折交叉检验中，每个样本有1次被当作测试样本，有6次被当作训练样本。 ×

第十一次

一.填空题*（共2题,25.0分）*

1

已知簇1中有点P1，簇2中有点P2、P3，点P1、P2、P3之间的距离如下表所示，使用全链法（最长距离法），求簇1和簇2之间的距离为 3

2
已知簇1中有点P1，簇2中有点P2、P3，点P1、P2、P3之间的距离如下表所示，使用单链法（最短距离法），求簇1和簇2之间的距离为 2

​

二.判断题*（共6题,75.0分）*

1K均值聚类的算法中，参数K就是希望得到的簇的数目 √

2K均值聚类的算法中，K个初始质心可以随机选择 √

3每次簇的质心更新后，将每个点指派到最远的质心 ×

4K均值聚类的算法中，随机选取的初始质心，一定可以保证得到好的聚类结果 ×

5对同一批数据进行两次K均值聚类，如果其中一次聚类结果的SSE更小，则说明这次聚类效果更好。 √

6K均值聚类容易受到离群点的影响。并且擅长处理非球形簇、不同尺寸和不同密度的簇。 ×

第十二次

一.填空题*（共3题,60.0分）*

1已知购物篮数据如下：{a,d,e}、{a,b,d,e}、{a,c,d,e}、{d,e}、{c,d,e}、{c,d}、{a,b,c}，求项集{a,b}的支持度等于 2/7 （答案请表示为最简分数形式x/y）

​

2已知购物篮数据如下：{a,d,e}、{a,b,d,e}、{a,c,d,e}、{d,e}、{c,d,e}、{c,d}、{a,b,c}，求规则{d,e}→{a}的置信度等于 3/5（答案请表示为最简分数形式x/y）

​

3已知购物篮数据如下：{a,d,e}、{a,b,d,e}、{a,c,d,e}、{d,e}、{c,d,e}、{c,d}、{a,b,c}，求规则{d,e}→{a}的支持度等于 3/7 （答案请表示为最简分数形式x/y）

二.判断题*（共2题,40.0分）*

1如果{a,d,e}是频繁项集，则{a,d}一定也是频繁项集 √

2如果{a,d,e}是非频繁的，则{a,b,d,e}也一定是非频繁的 √

问答题

1. 简述支持向量机的**”最大边缘“**原理

   答：既追求分类器泛化能力的最大化。既希望所找到的决策边界，在满足将两类数据点正确的分开的前提下，对应的分类器边缘最大。这样可以使得新的测试数据被错分的几率尽可能的小。

2. 简述软边缘支持向量机的基本工作原理

   对于存在数据污染、近似线性分类的情况，可能不存在一个最优的线性决策平面；当存在噪声数据时，为保证所有训练数据的准确分类，可能会导致过拟合。软边缘支持向量机通过引入松弛变量、惩罚因子，在一定程度上允许错误分类样本，以增大间隔距离。在分类准确度与泛化能力上寻求一个平衡点。

3. 简述非线性支持向量机的基本工作原理

   对于非线性可分的问题，可利用核交换，把原样本映射到某个高维特征空间。使得原样本在低维特征空间中非线性可分的样本，在新的高维特征空间中变得线性可分，并使用线性支持向量机进行分类

4. 简述K均值算法的步骤，选择1方面论述K均值算法可能遇到的问题及如何解决

   k均值的算法步骤：首先选择K个初始质心，既所期望的簇的个数。然后，每个点指派到最近的质心，而指派到一个质心的点集为一个簇，根据指派到的点更新每个簇的质心。重复指派和更新步骤，直到簇不发生变化，或者质心不发生变化

   

   存在的问题

   • 不同的初始质心将收敛得到不同的目标函数，可能只能达到局部最优解。

     

   • 随机选取初始质心，拙劣的初始质心，可能导致很糟糕的聚类结果。

   • 可能产生空簇

     替补质心，最远点或者最大see簇中的质心

     

   • 容易受到离群点的影响

     处理前删除离群点，或者处理时识别离群点

     [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uTiYYAzH-1593993456674)(D:/软件安装目录/Typora/upload/image-20200702202051015.png)]

   • 不能处理非球形簇、不同尺寸和不同密度的簇。

     [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RyZhckfo-1593993456674)(D:/软件安装目录/Typora/upload/image-20200702202149844.png)]

     

5. 以决策树算法为例，说明什么是模型过分拟合？模型过分拟合的原因有那些

   模型过分拟合：当训练数据拟合太好的模型，其** **哈可能比具有较高训练误差的模型高，称为模型过分拟合

   当决策树的规模变得太大时，即使训练误差还在继续降低，但检验误差开始增大，导致过分拟合。

   原因：

   • 存在噪声

     噪声点使得算法拟合了误标记的训练记录，导致对检验集合中记录误分类

   • 缺乏代表性样本

     由于训练数据缺乏代表性的样本，在没有多少训练记录的情况下，学习算法仍然细化模型就会产生过分拟合。

6. 属性的分类有哪4种？对每种属性类型各自有意义的运算有哪些

标称 只能判断是否相等

序数 判断是否相等和比较大小

区间 加减也有意义

比率 乘除也有意义

计算

1. 朴素贝叶斯分类

   

   

   

2. 计算数据集的熵，计算划分的期望

   

   

3. 计算欧式距离，KNN分类