VAE模型（详细推导+实例代码）

本文会从EM算法，GMM模型一步一步的的推导，在过渡到VAE模型，如果有熟悉的部分可以跳过。
Reference:

1. [苏剑林] https://spaces.ac.cn/archives/5253
2. Auto-Encoding Variational Bayes; arXiv:1312.6114 [stat.ML]
3. 李宏毅 机器学习课程第六讲
4. 机器学习白板推导 https://www.bilibili.com/video/BV1aE411o7qd/

EM算法

思路

首先回顾一下EM算法的过程：假设X是全体样本，$\theta$是全体参数。
那么MLE求解生成模型就是要求得一个$\theta$，使得$P(X|\theta )$最大。(因为假设X是抽自于某个分布)
也就是如下式子：
$$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}P(X|\theta )$$
一般为了方便求解，会加上一个log。
$$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}logP(X|\theta )$$
假设存在一个隐变量Z，这个隐变量可以生成X。
此时：

1. X称之为观测数据
2. Z称之为隐藏数据
3. (X,Z)称之为完全数据

于是我们可以改写上面式子(以下均为恒等变换，不懂的可以从右向左推一遍)
$$logP(X|\theta )=logP(X,Z|\theta )-logP(Z|X,\theta )$$
$$logP(X|\theta )=log\frac{P(X,Z|\theta )}{Q(Z)}-log\frac{P(Z|X,\theta )}{Q(Z)}$$
然后两边同时乘以Q(Z)(这里表示这个隐变量Z的一个先验分布)再对Z积分，得到
$$左边={\int }_{z}Q(Z)logP(X|\theta )dz=logP(X|\theta )$$
$$右边={\int }_{z}Q(Z)log[\frac{P(X,Z|\theta )}{Q(Z)}]dz-{\int }_{z}Q(Z)log[\frac{P(Z|X,\theta )}{Q(Z)}]dz$$

可以发现，右边的项是KL Divergence。也就是说：
$$-{\int }_{z}Q(Z)log[\frac{P(Z|X,\theta )}{Q(Z)}]dz=KL(Q(Z)||P(Z|X,\theta ))\ge 0$$
我们记左边的项为ELBo，也就是一个下界
那么
$$log(P(X|\theta ))=ELBo+KL\ge ELBo={\int }_{z}Q(Z)log[\frac{P(X,Z|\theta )}{Q(Z)}]dz$$
由于KL的非负性，所以上述等式成立，也就是说我们找到了$log(P(X|\theta ))$的一个下界。我们只需要不断地优化提高这个下界，就可以使得其目标函数不断提高（其实这里还需要证明收敛性，不过略过）

E步

当我们固定$\theta ,X$时，左边（$log(P(X|\theta ))$）是不变的，而右边我们想要提高下界ELBo。就可以通过最小化KL。KL最小时就是两个分布完全一致，也就说是当：
$$Q(Z)=P(Z|X,\theta )$$
时，ELBo最大，此时我们得到了Z的先验分布就是$Q(Z)=P(Z|X,\theta )$
注意，此时我们固定了$\theta$，所以我们不妨记此时的$\theta$为${\theta }^{(t)}$也就是当前t时刻的的值。
$$Q(Z)=P(Z|X,{\theta }^{(t)})$$

M步

在E步中找到了Q的分布后，我们需要寻找在当前Q下能够让$logP(X|\theta )$尽可能大的$\theta$。
也就是说我们要最大化ELBo：
$$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}{\int }_{z}Q(Z)log[\frac{P(X,Z|\theta )}{Q(Z)}]dz$$
我们替换ELBo的Q(Z)为M步得到的值，于是得到下面的式子：
$${\hat{\theta }}^{(t+1)}=\underset{\theta }{\mathrm{argmax}}{\int }_{z}P(Z|X,{\theta }^{(t)})log[\frac{P(X,Z|\theta )}{P(Z|X,{\theta }^{(t)})}]dz$$
我们把log中的除法拆成加法：
$${\hat{\theta }}^{(t+1)}=\underset{\theta }{\mathrm{argmax}}{\int }_{z}P(Z|X,{\theta }^{(t)})log[P(X,Z|\theta )]-P(Z|X,{\theta }^{(t)})log[P(Z|X,{\theta }^{(t)})]dz$$
可以发现，后面的$-P(Z|X,{\theta }^{(t)})log[P(Z|X,{\theta }^{(t)})$与$\theta$无关，所以可以舍弃。于是我们得到了M步的目标：
$${\hat{\theta }}^{(t+1)}=\underset{\theta }{\mathrm{argmax}}{\int }_{z}P(Z|X,{\theta }^{(t)})log[P(X,Z|\theta )]dz$$
我们可以进一步改写上面的式子为期望的形式：
$${\hat{\theta }}^{(t+1)}=E_{Z|X,{\theta }^{(t)}}[log[P(X,Z|\theta )]]$$

至此，期望最大化算法（EM）算法推导结束（除了收敛性证明）

直观感觉

直观的来看EM算法的两步可以归为如下步骤：

1. 固定$\theta$，然后寻找Z的先验P(Z)，使得ELBo尽可能的大
2. 解除$\theta$的固定，然后在E步找到的P(Z)的前提下，最大化ELBo提升下界

GMM模型

高斯混合模型是一种生成模型，它假定存在着一个隐变量Z，Z是一个离散的概率分布，有K个取值，如下：
$$\begin{gathered} Z=1,\mathrm{2..},k \\ P(Z=i)=p_i(i\in \{1,\mathrm{2..},k\}) \\ \sum _i{p}_i=1 \end{gathered}$$
然后，我们所要建模$P(X|\theta )$由k个高斯分布乘以对应的z的概率值构成，也就是：
$$P(X|\theta )=\sum _{i=1}^k{p}_{i}N(X|{\Sigma }_i,{\mu }_i)$$
也就是说，有K个高斯分布组成了要建模的分布，这K个高斯分布的线性组合就是我们要求的分布。
其中：
$$\theta =\{{\Sigma }_1,{\Sigma }_2...{\Sigma }_k,{\mu }_1,{\mu }_2...,{\mu }_k,p_1,p_2...p_k\}$$

GMM模型显然是一个含有隐变量的模型，二期我们可以直接通过EM算法来进行求解，但这里主要是为了讲解VAE。所以不写如何求解GMM了。

VAE

VAE思想

VAE的假设很简单：

1. 存在着隐随机变量Z，该变量有一个先验分布$P_{\theta }(Z)$
2. 从先验分布$P_{\theta }(Z)$中抽取样本z
3. 由样本z得到条件分布$P_{\theta }(X|Z=z)$，然后抽样得到X

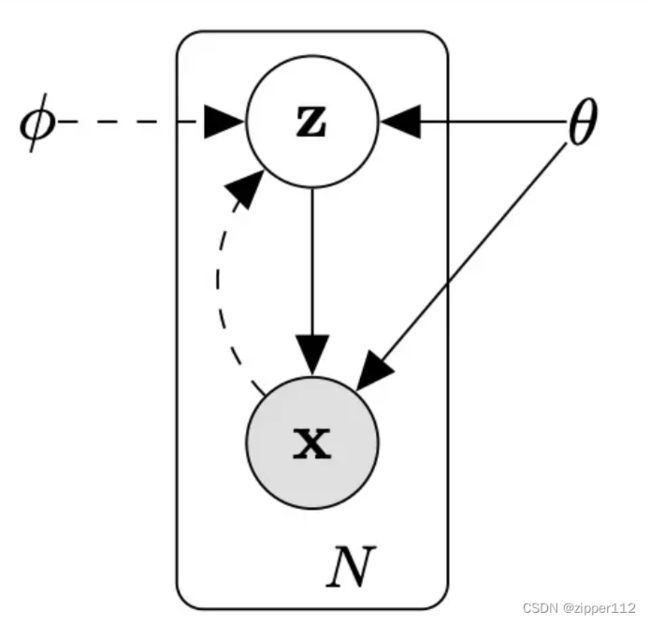
如上图所示，隐变量Z决定了X的生成$(先忽略参数\varphi )$
以上就是VAE假设的样本生成过程。

从GMM到VAE

可以看到和GMM非常相似，但是这里VAE与GMM有所不同，因为VAE假设的Z是高维，连续的，这就带来了几个问题：
$$P_{\theta }(X)={\int }_z{P}_{\theta }(Z)P_{\theta }(X|Z)dz$$
上述式子是我们熟悉的概率乘条件概率的式子，相当于GMM中的高斯分布线性组合。不过这里显然是无穷个高斯分布（因为积分是连续的）。

但是比较尴尬的问题出现了，这个积分是高维的，我们无法对其求解（也就是说是intractable的）。也就是说我们求解得到$P(X)$。

那么用EM算法是否可以呢？这里也很难，因为EM算法的E步骤需要令:
$$Q_{\theta }(Z)=P_{\theta }(Z|X)$$
而$P_{\theta }(Z|X)$而想要求这个分布也是intractable（因为需要用到$P(X)$），所以我们无法直接求出。

于是我们改其道而行，我们另外找一个分布$q_{\theta }(Z|X)$我们让这个分布无限的去逼近$P_{\theta }(Z|X)$，也就是说两者的KL散度最小。

公式推导

我们重回到EM算法的最开始步骤，我们将第i个样本P(x^{(i)})拆解为KL和ELBo
$$logP(x^{(i)})=ELBo+KL\ge ELBo$$
注意，KL的公式如下：
$$KL(q(z)|P(z|x^{(i)},\theta ))$$
我们把$q(z)$替换为$Q_{\varphi }(z|x^{(i)})$，于是就可以发现，其实我们就是在逼近这两者的分布。
于是我们得到了:
$$logP(x^{(i)})\ge ELBo=E_{Q_{\varphi }(z|x^{(i)})}[log{P}_{\theta }(x^{(i)},z)-log{Q}_{\varphi }(z|x^{(i)})]$$
这是一个下界，显然如同EM一样，我们只需要提高这个下界就可以不断地扩大$logP(x^{(i)})$还能同时把$Q_{\varphi }(z|x^{(i)})$给解出来。

我们进一步的进行变形(一下X可以看做是$x^{(i)}$)：
$$\begin{gathered} E_{Q_{\varphi }(Z|X)}[log{P}_{\theta }(X,Z)-log{Q}_{\varphi }(Z|X)]= \\ {E}_{Q_{\varphi }(Z|X)}[log{P}_{\theta }(X|Z)+log{P}_{\theta }(Z)-log{Q}_{\varphi }(Z|X)]= \\ {E}_{Q_{\varphi }(Z|X)}[log{P}_{\theta }(X|Z)+log\frac{P_{\theta }(Z)}{Q_{\varphi }(Z|X)}]= \\ {E}_{Q_{\varphi }(Z|X)}[log{P}_{\theta }(X|Z)]-KL(Q_{\varphi }(Z|X)||P_{\theta }(Z)) \end{gathered}$$
于是我们得到了最终的形式：
$$logP(x^{(i)})\ge E_{Q_{\varphi }(z|x)}[log{P}_{\theta }(x^{(i)}|z)]-KL(Q_{\varphi }(z|x^{(i)})||P_{\theta }(z))$$
从上面我们可以看出一些有意思的事，我们期望最大化ELBo，也就是说我们要最小化$KL(Q_{\varphi }(z|x^{(i)})||P_{\theta }(z))$

就是说让这两个分布尽可能的接近，也就是说这里其实$Q_{\varphi }(z|x^{(i)})$近似了$P_{\theta }(z)$。
这里可以看做一定encode的能力，给定数据X，然后生成隐变量的值Z。
然后另一部分可以看做要最大化给定Z时，还原出X的期望。也就是Decode的过程。

至此从优化的目标函数上来看，我们已经找到了Encoder和Decoder的两个相关优化目标。
到这里，为了优化这个目标，我们可以使用梯度上升的的方式，也就是对$\varphi$进行求导，然后再用蒙特卡洛采样得到梯度的近似值。

我们记
$$L(\theta ,\varphi ;x^{(i)})=ELBo=E_{Q_{\varphi }(z|x^{(i)})}[log{P}_{\theta }(x^{(i)},z)-log{Q}_{\varphi }(z|x^{(i)})]$$
我们令$f(z)=log{P}_{\theta }(x^{(i)},z)-log{Q}_{\varphi }(z|x^{(i)})$
那么我们要求的梯度就是(以下$Q_{\varphi }(z|x^{(i)})$记做$Q_{\varphi }$)
$$\begin{gathered} {\nabla }_{\varphi }{E}_{Q_{\varphi }}[f(z)]={\nabla }_{\varphi }{\int }_z{Q}_{\varphi }f(z)dz={\int }_z{\nabla }_{\varphi }{Q}_{\varphi }f(z)dz \\ ={\int }_{z}f(z)Q_{\varphi }{\nabla }_{Q_{\varphi }}log(Q_{\varphi })dz=E_{Q_{\varphi }}[f(z){\nabla }_{Q_{\varphi }}log(Q_{\varphi })] \end{gathered}$$
这里其实利用到了一个很有趣的性质$f^{\prime }(x)=f(x)\ast (logf(x){)}^{\prime }$于是把原本求的积分内的梯度再次变回了一个期望的形式。
而这个期望就可以使用蒙特卡洛的方式进行近似逼近了。

但是此时存在着一个问题

如图是VAE原论文中的蒙特卡洛近似后的结果，也就是用随机采样的得到的样本的计算后的均值近似原本的均值，这里存在着一个$z^{(l)}$，是从$Q_{\varphi }(z|x^{(i)})$中抽样的，这个log就会造成很大的方差（因为越靠近0，就越陡峭）。

蒙特卡洛估计本身就是近似，方差又打再加上随机梯度下降的不确定性。所以导致很难进行优化。于是就引入了重参数技巧.

重参数

之所以出现了log，是因为对原本作为期望的分布$Q_{\varphi }(z|x^{(i)})$进行了求导。于是坐着引入了一个新的变量$ϵ$，这个变量来与z产生关系：
$$\begin{gathered} \tilde{z}\sim g_{\varphi }(ϵ,x^{(i)}) \\ ϵ\sim p(ϵ) \end{gathered}$$
可以注意到：
$$\int Q_{\varphi }(z|x)f(z)dz=\int p(ϵ)f(z)dϵ=\int p(ϵ)f(g_{\varphi }(ϵ,x^{(i)}))dϵ$$

此时我们就可以直接的估计出$E_{Q_{\varphi }}[f(z)]$
于是我们就得到：
$$E_{Q_{\varphi }}[f(z)]=E_{p(ϵ)}[f(g_{\varphi }(ϵ,x^{(i)}))]$$
于是我们得到了一个估计值：
$$\begin{gathered} E_{p(ϵ)}[f(g_{\varphi }(ϵ,x^{(i)}))]\approx \frac{1}{L}\sum _{i=1}^{L}f(g_{\varphi }({ϵ}^{(i)},x^{(i)})) \\ 其中{ϵ}_i采样于p(ϵ) \end{gathered}$$
然后我们重写L的式子：
$$L(\theta ,\varphi ;x^{(i)})=ELBo=E_{p(ϵ)}[log{P}_{\theta }(x^{(i)},z)-log{Q}_{\varphi }(z|x^{(i)})]$$
$$\begin{gathered} =\frac{1}{L}\sum _{l=1}^{L}log{P}_{\theta }(x^{(i)},g_{\varphi }({ϵ}^{(l)},x^{(i)}))-log{Q}_{\varphi }(g_{\varphi }({ϵ}^{(l)},x^{(i)})|x^{(i)}) \\ 其中{ϵ}_i采样于p(ϵ) \end{gathered}$$

由于KL散度经常可以直接被计算出来，所以我们也可以写成如下的式子：
$$\begin{gathered} =-KL(Q_{\varphi }(z|x^{(i)})||P_{\theta }(z))+\frac{1}{L}\sum _{l=1}^{L}log{P}_{\theta }(x^{(i)}|g_{\varphi }({ϵ}^{(l)},x^{(i)})) \\ 其中{ϵ}_i采样于p(ϵ) \end{gathered}$$
此时上述的式子就是近似可微的了，这个结果可以直接通过SGD求解。

VAE+神经网络

我们来举一个VAE+神经网络的例子，我们具体化上述抽象的分布和函数：

1. $g_{\varphi }(x^{(i)},{ϵ}^{(l)})={\mu }^{(i)}+{\sigma }^{(i)}\odot {ϵ}^{(l)}$
2. $ϵ\sim N(0,I)$
3. $z\sim N(0,I)$
4. $Q_{\varphi }(z|x^{(i)})=N(Z;{\mu }^{(i)},{\sigma }^{2(i)}I)$
   上述的${\mu }^{(i)}$和${\sigma }^{2(i)}$都是由x得到的，也就是说我们需要训练一个encoder，来输入x获得上述两个部分：
   $$encoder(x^{(i)})=({\mu }^{(i)},{\sigma }^{2(i)})$$
   其中这个encoder就是一个神经网络。
   然后我们用另一个神经网络来拟合概率分布$p_{\theta }(x|z)$
   于是就有了decoder。
   接下来我么们来计算损失函数：
   $$\begin{gathered} L(\theta ,\varphi ;x^{(i)})=-KL(Q_{\varphi }(z|x^{(i)})||P_{\theta }(z))+\frac{1}{L}\sum _{l=1}^{L}log{P}_{\theta }(x^{(i)}|g_{\varphi }({ϵ}^{(l)},x^{(i)})) \\ 其中{ϵ}_i采样于p(ϵ) \end{gathered}$$

第二项变成：
$$\frac{1}{L}\sum _{l=1}^{L}log{P}_{\theta }(x^{(i)},g_{\varphi }({ϵ}^{(l)},x^{(i)}))=\frac{1}{L}\sum _{l=1}^{L}log{P}_{\theta }(x^{(i)}|{\mu }^{(i)}+{\sigma }^{(i)}\odot {ϵ}^{(l)})$$

而第一项KL散度通过积分可以得到：
（这里的具体推导可以看下面另一个视角的VAE那里）

其中J是$\sigma$的维度。

然后就是decoder损失函数的选择：
如果是二值数据，那么此时可以使用n重伯努利分布：
$$P_{\theta }(x|z)=\prod _{k=1}^{D}p(z{)}_k^{x_k}(1-p(z{)}_k{)}^{(1-x_k)}$$
$$-log{P}_{\theta }(x|z)=\sum _{k=1}^D-x_{k}logp(z{)}_k-(1-x_k)log(1-p(z{)}_k)$$
可以看到这其实就是cross entropy。也就是交叉熵作为损失函数。

如果是一般的数据可以使用正态分布作为损失函数：
我们固定正态分布的sigma，就得到：
$$P_{\theta }(x|z)=\frac{1}{C_1}ex{p}^{-C_2||x-\mu (z)|{|}^2}$$
当方差固定时，正态分布的一些参数可以用两个常数$C_1,C_2$代替，如上图。然后取对数
$$-log{P}_{\theta }(x|z)=-log(\frac{1}{C_1})+C_2||x-\mu (z)|{|}^2\approx ||x-\mu (z)|{|}^2$$
也就是说是MSE损失函数，其中$\mu (z)$可以看作是decoder的输出。

然后是采样，由于有多个epoch，所以每次采样一个就够了。
接下来上代码：
我们用交叉熵做损失函数，同时使用Minist作为数据集训练

from torch import nn
import torch

class VAE(nn.Module):
    def __init__(self, image_size=28, z_dim=100) -> None:
        super().__init__()

        self.encoder = nn.Sequential( #由若干卷积和一个全连接构成encoder
            nn.Conv2d(in_channels=1, out_channels=20, kernel_size=3),
            nn.ReLU(),
            nn.Conv2d(in_channels=20, out_channels=20, kernel_size=3),
            nn.ReLU(),
            nn.Flatten(start_dim=1),
            nn.Linear(in_features=11520, out_features=800),
            nn.ReLU()
        )
        self.sigma = nn.Linear(800, z_dim)
        self.mu = nn.Linear(800, z_dim)
        self.sigmoid = nn.Sigmoid()

        self.decoder = nn.Sequential( # 两个全连接构成decoder
            nn.Linear(in_features=z_dim, out_features=2000),
            nn.ReLU(),
            nn.Linear(in_features=2000, out_features=image_size * image_size)
        )

    def reparameterize(self, sigma, mu): # 冲参数计算，计算z
        sigma = torch.exp(sigma / 2) # 这里sigma可能非正，所以加了exp，然后开根号
        eps = torch.rand_like(sigma) # 抽样得到epsilon
        return mu + eps * sigma

    def encode(self, x):
        hidden = self.encoder(x)
        sigma, mu = self.sigma(hidden), self.mu(hidden)
        return sigma, mu
    
    def decode(self, z):
        return self.decoder(z)
    
    def forward(self, x):
        sigma, mu = self.encode(x)
        z = self.reparameterize(sigma, mu)
        return sigma, mu, self.sigmoid(self.decode(z)) # 这里的sigmoid是为了计算交叉熵损失
    

def loss_function(sigma, mu, x, reconstruct):
    BCE_loss = nn.BCELoss(reduction='sum')
    kl_divergece = -0.5 * torch.sum(1 + sigma - torch.exp(sigma) - mu ** 2) # 这里的sigma本来应该是正的，所以用exp来代替了
    x = torch.flatten(x, start_dim=1)
    cross = BCE_loss(reconstruct, x) # 交叉熵部分
    return kl_divergece + cross

下面是训练的部分

from model import VAE, loss_function
import torch
import torchvision
from torch.utils.data import DataLoader
from torchvision.utils import save_image

if __name__ == '__main__':
    BATCH_SIZE = 150
    LR = 0.001
    EPOCH = 100

    model = VAE().cuda()
    optim = torch.optim.Adam(lr=LR, params=model.parameters())
    data = torchvision.datasets.MNIST('./data', train=True, transform=torchvision.transforms.ToTensor(), download=True)
    dataloader = DataLoader(dataset=data, batch_size=BATCH_SIZE, shuffle=True)

    for epoch in range(EPOCH):
        for i, (imgs, labels) in enumerate(dataloader):
            imgs = imgs.cuda()
            sigma, mu, recon = model(imgs)

            loss = loss_function(sigma, mu, imgs, recon)

            optim.zero_grad()
            loss.backward()
            optim.step()
            if i % 50 == 0:
                print('loss', loss.item())
                fake_images = recon.view(-1, 1, 28, 28)[:5]
                x_concat = torch.cat([imgs.view(-1, 1, 28, 28)[:5, :], fake_images], dim=3)
                save_image(x_concat, 'generate_images/generate_images-{}-{}.png'.format(epoch + 1, i))
        torch.save(model.state_dict(), './model.pkl')

图中是数字对，每一对左边是原图，右边是VAE重建后的图片。
到此，VAE结束

另一个视角的VAE

思想

上述是从贝叶斯视角来看VAE的，全部都是公式，非常的不直接，让扔一头雾水，下来来从更intuitive的角度来看VAE：
先来看，高斯混合模型，相当于是把若干个高斯模型迭代并分别乘以一个离散的概率分布的概率作为权重：

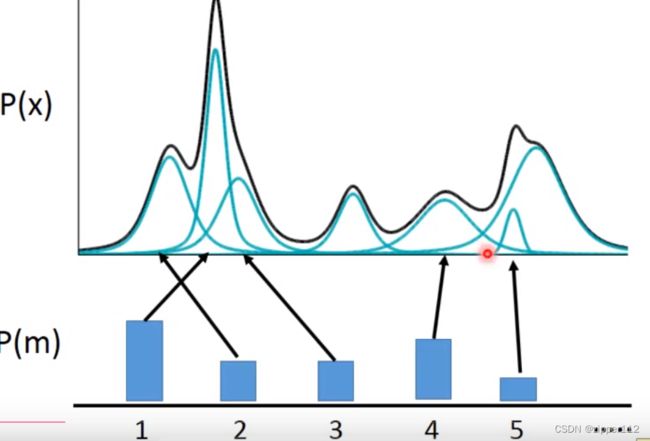
其中P(m)就是这个概率，也是上面所说的隐变量z。
然后直观地来看，我们把这个高斯混合模型给一般化，把P(m)编程高维分布，也变成连续的分布，就得到了VAE：

如图，此时的z就是个标准的高维的正态分布。

其中我们有一项$P(x|z)$这个我们用神经网络去模拟：

输入一个z，输出均值和方差，他们都是z的函数。
理论上来说到这里看似很完美了，P(z)是标准正态分布是已知的，而且$P(x|z)$可以通过神经网络训练得来。似乎所有问题都解决了。

为什么引入encoder

但是问题在于这没法实现，首先，我们的目标是最大化似然函数$P(X|\theta )$，然后似然可以被拆做：
$$P_{\theta }(X)={\int }_z{P}_{\theta }(Z)P_{\theta }(X|Z)dz$$
这个积分是无法积出来的，因为后项$P_{\theta }(X|Z)$是个神经网络。这样我们得不到损失函数。

另一个问题在于，P(z)与x是没有对应关系的，同一个P(z)抽出来的样本，可以对应相同的x。这可能会造成一系列麻烦：
于是VAE引入了另一个分布$Q(z|x)$来取代原来的$P(z)$，这样解决了z没有指向性的问题。当然这个$Q(z|x)$也是正态分布，我们也用一个神经网络去模拟：

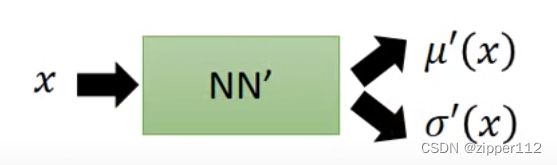
输入一个x，同样的输出两个参数作为输出结果。

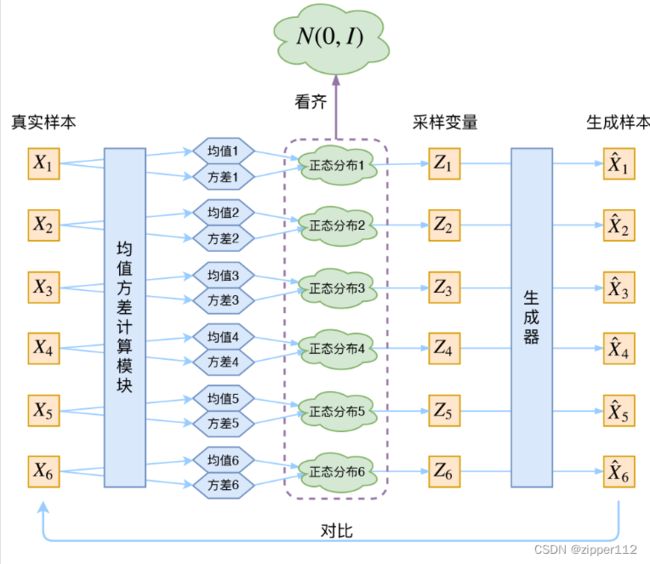
这样似乎我们的问题就解决了，但仍然存在问题：

如上图（来自于苏剑林的博客），是我们的步骤，这里有一个大问题那就是我们希望采样得到的z是的不确定性是由神经网络自己生成的（也就是方差sigma）。

也就是说神经网络完全可以偷懒，让这个方差直接为0，然后我们希望引入的采样的随机性就没了。于是我们引入了正则项，来要求$Q(z|x)$朝着标准正态分布的方向逼近，也就是我们之前假设的先验分布P(z)：
下面$z_k$表示z的第k个纬度，$x^{(i)}$表示第i个样本

也就是$$\min KL(N(\mu (x^{(i)}),\sigma (x^{(i)}))||N(0,I))={\int }_{z}N(\mu (x^{(i)}),\sigma (x^{(i)}))ln\frac{N(\mu (x^{(i)}),\sigma (x^{(i)}))}{N(0,I)}dz$$
我们假设各个分量之间是独立的，于是我们只用计算出第k维度即可
$${\int }_{-\infty }^{+\infty }\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}ln\frac{\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}}{\frac{1}{\sqrt{2\pi }}{e}^{-\frac{z_k^2}{2}}}d{z}_k$$
我们把后项进行化简：
$$=\frac{1}{2}{\int }_{-\infty }^{+\infty }\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}(-ln{\sigma }_k^2(x^{(i)}))+z_k^2-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{{\sigma }_k(x^{(i)}{)}^2})d{z}_k$$
可以看到后面有三项需要分别和第一项相乘然后积分：
首先是：
$$-\frac{1}{2}{\int }_{-\infty }^{+\infty }\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}ln{\sigma }_k^2(x^{(i)}))d{z}_k=-\frac{1}{2}ln{\sigma }_k^2(x^{(i)})$$
因为上述的积分就是个概率分布的积分，最后结果为1，$-\frac{1}{2}ln{\sigma }_k^2(x^{(i)})$与x无关
$$\frac{1}{2}{\int }_{-\infty }^{+\infty }\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}{z}_k^{2}d{z}_k$$
这就是二阶中心距：
$${\mu }_k(x^{(i)}{)}^2+{\sigma }_k(x^{(i)}{)}^2$$
最后一项，展开之后得到：
$$\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{{\sigma }_k(x^{(i)}{)}^2}=\frac{(z_k^2-2z_k{\mu }_k(x^{(i)})+{\mu }_k(x^{(i)}))}{{\sigma }_k(x^{(i)}{)}^2}$$
中间和前面相乘后积分直接为0，前面和后面也可以用二阶中心距和概率分布的定义直接计算
最后得到结果为-1
于是
$${\int }_{-\infty }^{+\infty }\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}ln\frac{\frac{1}{\sqrt{2\pi {\sigma }_k^2(x^{(i)})}}{e}^{-\frac{(z_k-{\mu }_k(x^{(i)}){)}^2}{2{\sigma }_k(x^{(i)}{)}^2}}}{\frac{1}{\sqrt{2\pi }}{e}^{-\frac{z_k^2}{2}}}d{z}_k=\frac{1}{2}(-ln{\sigma }_k^2(x^{(i)})+{\mu }_k(x^{(i)}{)}^2+{\sigma }_k(x^{(i)}{)}^2-1)$$

为什么要重参数

然后是采样操作，实际上采样操作是不可行的，因为采样出来的值没法后续用X来进行优化（因为前半部分的encoder只有一个KL损失在约束，不受到后面的decoder的梯度传播）

所以必须要引入一个新变量来把采样过程的随机性独立出来，这就是重参数技巧
$$P(z|x)=\frac{1}{\sigma (x^{(i)})\sqrt{2\pi }}{e}^{-\frac{(x-\mu (x^{(i)}){)}^2}{2\sigma (x^{(i)}{)}^2}}\sim N(\mu (x^{(i)}),\sigma (x^{(i)}{)}^2)$$
我们引入另一个标准正态分布
$$ϵ\sim N(0,I)$$
可知
$$ϵ\ast \mu (x^{(i)})+\sigma (x^{(i)})\sim N(\mu (x^{(i)}),\sigma (x^{(i)}{)}^2)$$
也就是说我们可以用这个$ϵ$对一个与神经网络无关的标准正态分布采样，然后通过如下公式在转换为z
$$ϵ\ast \mu (x^{(i)})+\sigma (x^{(i)})=z$$
这就是重参数技巧的实质。

噪声与重建

VAE的KL损失及部分实际上是一个正则化部分，它让模型尽可能的保持一定的噪声。而VAE的重建损失（Reconstruct Loss）则是尽可能的去在有噪声的情况下回复原图。这实际上是一个对抗的过程。

从另一个角度来看，VAE其实也是在希望模型能够不在一个点上学到会付出这个输出，而是在一个范围之类（噪声的影响范围）之内恢复出一个数据

Discrete VAE

以后再写吧