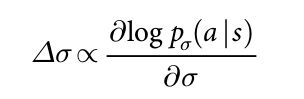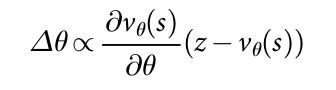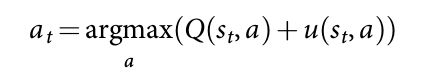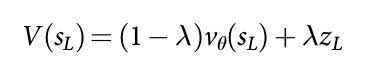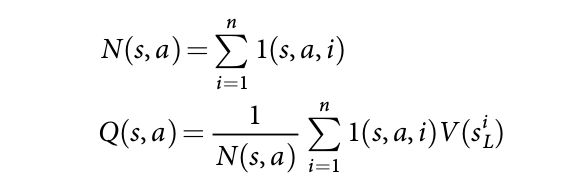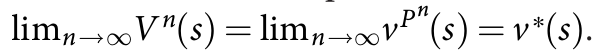Mastering the game of Go with deep neural networks and tree search
Nature 2015
这是本人论文笔记系列第二篇 Nature 的文章了,第一篇是 DQN。好紧张!好兴奋!
本文可谓是在世界上赚够了吸引力!
围棋游戏被看做是 AI 领域最有挑战的经典游戏,由于其无穷的搜索空间 和 评价位置和移动的困难。本文提出了一种新的方法给计算机来玩围棋游戏,即:利用 "value network" 来评价广泛的位置 和 “policy networks”来选择移动操作。这些神经网络通过人类专家的游戏棋谱监督学习 和 自己跟自己玩的强化学习的巧妙结合。没有任何回头的搜索,神经网络玩该游戏达到了 蒙特卡罗树搜索程序的顶尖水平来模拟自己跟自己玩的 self-play。我们也引入了一个新的搜索算法来结合 MC 模拟 和 value and policy networks。利用该搜索算法,我们的 AlphaGo 可以达到 99.8% 的赢的局面,当对抗其他围棋游戏时候,并且以 5:0 的大比分 击败了 欧洲围棋世界冠军!这是在围棋领域,计算机程序第一次击败人类专业玩家,并且之前一直认为这项记录至少要往后推迟一个世纪才会发生!
带有完美信息的所有游戏都有一个最优的 value function $v^*(s)$,这个决定了游戏的输出,在所有玩家完美的操作下,从每一个广泛的位置或者状态 s。这些游戏可以通过迭代的计算最优 value function 从一个包含大约 $b^d$次方个移动的序列的搜索树,其中 b 是游戏的 breadth(每一个动作合法移动操作的数目),d 是其深度(游戏长度)。在一个大型游戏中,例如: chess (b ≈35,d ≈80),围棋(b≈250,d≈150),充分的搜索是不可能的,但是有效的搜索空间可以通过两个主要的原则进行缩减:
首先,搜索的宽度可以通过位置评价进行降低:将搜索树在状态 s 上进行截断,然后在 s 之后的子树,用一个估计的 value function v(s) ≈$v^*(s)$ 来预测从状态 s 得到的结果。这种方法已经在很多领域得到了超人的效果,但是仍然无法解决 围棋的问题,由于该问题过于复杂。
第二,搜索的 breadth 可以通过根据策略 采样动作来降低,这是一个在位置 s 上的可能动作 a 的概率分布。
例如,Monte Carlo rollouts search 来最大化深度,而没有 branching,从一个策略 p 上进行动作的长序列采样。平均这样的 rollouts 可以提供有效的位置评价(position evaluation),达到超人的效果。
Monte Carlo tree search(MCTS)利用蒙特卡洛 rollouts 来预测在一个搜索树上面的每一个状态的值。随着执行更多的模拟,搜索树变得越来越大,相关值变得越来越精确。策略被用来在搜索的过程中选择动作也随着时间而逐渐改善,通过选择带有更高值的孩子。这个策略收敛到一个最优的 play,评价收敛到一个最优的值函数。当前最强的围棋程序是基于 MCTS,利用策略进行训练来预测人类玩家的移动。这些策略都被用来减少搜索的范围而实现高概率动作的选择,在 rollouts的过程中进行采样动作。这种方法已经达到了很强的业余玩家的水平。然而,之前的工作一般都被限制在浅层的策略或者值函数,基于输入特征的现行组合。
最近,深度卷积神经网络已经在视觉领域取得了瞩目的成就:图像分类 人脸识别 以及 打游戏 Atari games 等等。他们利用多层神经元,重叠起来,来构建一个递增的摘要,一张图像定位的表达。我们采用一个类似的结果来给围棋这个游戏程序。我们采用 19 * 19 的图像来作为输入,利用卷基层构建位置的表示。我们利用这些神经网络来有效的降低搜索树的深度 和 广度 问题:
evaluating positions using a value network, and sampling actions using a policy network。
利用价值网络来评价位置,利用策略网络来采样动作。
我们利用由几个 ML 的几个阶段构成的流程来训练神经网络。我们开始直接从专家棋谱移动上,训练一个监督学习策略网络。这提供了一个快速的 有效的利用立刻的反馈 和 高质量的梯度来学习更新。我们也训练了一个快速的策略 可以在 rollouts 的过程中快速的采样动作。接下来,我们训练一个 RL 策略网络 来改善 SL 策略网络,通过优化自学习最终的输出。这样调整策略朝向赢下这个游戏的方向前进,而不是最大化预测的精度。最后,我们训练一个值网络通过 RL 策略网络来预测游戏的赢家来对抗自己。我们的程序 AlphaGo 利用MCTS 有效的结合了策略 和 值网络(value networks)。
Supervised Learning of Policy Networks:
对于训练流程的第一个阶段,我们利用监督学习直接基于前人的工作来预测专家的移动动作。该 SL policy network 由卷积层 和 非线性激活函数构成,最后是 softmax layer 输出所有合法动作 a 的概率分布。输入的 s 给策略网络,是一个简单的 board 状态的表示。该策略网络是在随机采样的 状态-动作对(s, a)上进行训练的,利用 stochastic gradient ascent 来最大化在状态 s 下,人类选择移动 a 的似然估计:
我们从 KGS Go Server上的 30 百万 位置上训练了一个 13 层的策略网络,我们称之为:SL policy network。该网络利用所有输入特征预测正确人类走棋方式的概率是 57.0%,只用原始的 board position 和 移动历史作为输入的话,则为:55.7%,相比于其他研究小组的 44.4% 算是有很大的提升了。在精度上很小的改善就可以在后面发挥巨大的作用;更大型的网络可以得到更好的结果,但是与至增加的是搜索过程中较慢的评价。我们也训练了一个快速但是不太准确的 rollouts 策略,利用一个带有权重的小模块特征的线性 softmax,精度是 24.2%,仅用了 2 微秒就可以选择一个动作,而不是策略网络的 3 毫秒。
Reinforcement Learning of Policy Networks
流程训练的第二个阶段是为了改善策略网络,通过策略梯度强化学习的方法。这个 RL 策略网络是和 SL Policy Network 相同的结构,其权重被初始化相同的值。我们在当前 策略函数 和 一个随机选择的策略网络之前的迭代交替的进行。利用这种方式从一个成分池子中随机化通过阻止当前策略的过拟合来稳定训练。我们采用奖励函数 r(s)对于所有的非终端时间步骤 t < T 都是 0 。输出是游戏结束时候的终止奖赏,从当前玩家在时间步骤 t 的角度:
赢了则奖赏 +1; 输了则奖赏为 -1.
然后通过随机梯度上升的方法来更新权重,朝向最大化期望输出的方向进行:
我们在玩游戏的过程中评价 RL policy network 的性能,从其输出概率分布上,采样每一个 move $a_t$。When play head-to-head,RL 策略网络比 SL 策略网络赢棋的概率是 80% 。我们也测试了最强的开源围棋算法,Pachi,一个顶尖的蒙特卡洛搜索程序,每一个移动会执行 100,000 次模拟。根本没有利用搜索,RL policy network 比 Pachi 赢棋的概率高了 85% 。对比起来看,之前的顶尖算法,仅仅依赖于监督学习,对比 Pachi 赢了 11%,以及对抗较弱的程序 Fuego 赢的概率是 12% 。
Reinforcement Learning of value Networks :
最后一个训练阶段是集中于位置评价(value evaluation),预测一个 value function $v^p(s)$ 从利用策略 p 得到的位置 s 出发预测一个输出:
理想情况下,我们想知道在 perfect play $v^*(s)$ 下的最优值函数(optimal value function);实际上,我们利用 RL policy network 来给我们最强的策略,预测 value function。我们利用权重为 $\theta$ 的value network $v_{\theta}(s)$,即:$v_{\theta}(s) ≈ v^{p_\rou}(s) ≈ v^*(s)$。这个神经网络和 policy network 有类似的结构,但是只是输出单个的预测,而不是一个概率分布。我们在 state-outcome pairs (s, z) 上进行回归来训练 value network 的权重,利用随机梯度下降的方法来最小化 predicted value $v_\theta(s)$ 和 对应的输出 z 之间的均方误差(the mean squared error(MSE)):
采用 naive 的方法,从完整的游戏数据来预测游戏的输出会导致 overfitting, 问题就在于连续的位置是强烈相关的,区别仅仅在于一个棋子(stone),但是回归的目标是整个游戏共享的。当用这种方法在 KGS 数据集上进行训练的时候,value network 记住了游戏的输出,而不是产生新的位置,在测试集上最小化 MSE 0.37,训练集上是 0.19 。为了解决这个问题,我们产生了一个新的 self-play dataset 由 30 百万个不同的位置构成,每一个都从单独的游戏中采样而来。每一个游戏都在 RL policy network 和 它自己之间来回切换,直到游戏终止。在这个数据集上进行训练就会使得 MSE 在训练集 和 测试集上分别为 0.226 和 0.234,表明最小化的 overfitting。
Search with Policy and Value Networks
AlphaGo 在 MCTS 算法中结合了 policy and value networks,通过一直向前搜索选择动作。每一个搜索树的 edge (s, a)存贮了一个 action value Q(s, a),访问次数 N(s, a),以及一个先验概率 P(s, a)。该树从根节点开始通过模拟进行遍历(descending the tree in complete games without backup)。在每次 simulation 的时间步骤 t 上,从状态 $s_t$ 下选择一个动作 $a_t$:
为了最大化 action value 加上一个 bonus:
这个和 先验概率成正比,但是随着访问次数而逐渐衰减,以实现鼓励探索。当在第L步,访问达到了一个 叶子节点 $s_L$,该叶子节点被扩充。叶子的位置 %s_L% 只被 SL Policy networks 处理一次。输出概率存储为先验概率 P 对于每一个合法的动作 a,$P(s, a) = p_{\delta}(a|s)$。叶子节点以两种不同的方式进行评价:
首先,通过 value network ;
第二,一个随机的 rollout 的输出 $z_L$被执行,直到终止步骤 T,利用一个快速的 rollouts policy $p_{\pi}$;
这两个策略被组合起来,利用一个混合的参数 $\lambda$,融合进叶子评价 $V(s_L)$:
在模拟结束的时候,action values 和 访问次数统计都被更新。每一个 edge 通过那个边的所有模拟的 累计访问次数 和 所有模拟的均值评价:
其中,$s^i_L$ 是第 i 次模拟的叶子节点,$l(s, a, i)$ 表明是否 edge (s, a)在第 i 次模拟的过程中被访问。当该搜索完成的时候,该算法从 root position 选择访问次数最多的移动。
需要注意的是 SL policy network 在AlphaGo 中表现更好,比起 RL policy network,可能是因为人类选择 a diverse beam of promising moves, 而 RL 优化单个最优移动。然而从 stronger RL policy network 上得到的 value function 比从 SL policy network 得到的 value function 要好!
评价一个策略和 value networks 需要比传统搜索方法要高几个量级的计算量。为了有效的结合 MCTS 和 深度神经网络,AlphaGo 利用了多线程搜索,在 CPUs 上搜索,在 GPUs 上进行计算策略 和 value networks。最终版本的 AlphaGo 采用了 40个线程和 48个 CPUs,8个 GPUs。还采用了 AlohaGo 的分布式版本,有点小变态!
Evaluating the Playing strength of AlphaGo
效果明显,完爆其他围棋游戏,以及 5:0 击败欧洲围棋冠军!
Discussion:
暂时没啥说的,只能说太刁了!!!
基础补充:
1. MCTS 蒙特卡罗搜索树(简介):
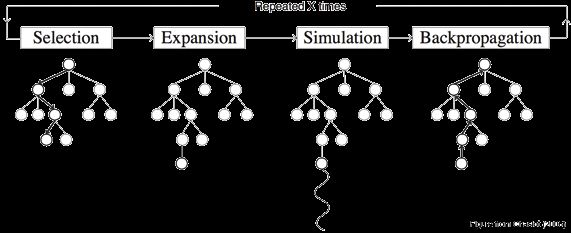
大体上可以分为一下几个步骤:
- 选择 Selection:从根节点 R 开始,递归选择最优的子节点(后面会解释)直到达到叶子节点 L。
- 扩展 Expansion:如果 L 不是一个终止节点(也就是,不会导致博弈游戏终止)那么就创建一个或者更多的字子节点,选择其中一个 C。
- 模拟 Simulation:从 C 开始运行一个模拟的输出,直到博弈游戏结束。
- 反向传播 Backpropagation:用模拟的结果输出更新当前行动序列。
原文链接:http://www.jianshu.com/p/d011baff6b64#
著作权归作者所有,转载请联系作者获得授权,并标注“简书作者”。
每个节点并需包含两个重要的信息:一个是根据模拟结果估计的值和该节点已经被访问的次数。
按照最为简单和最节约内存的实现,MCTS 将在每个迭代过程中增加一个子节点。不过,要注意其实根据不同的应用这里也可以在每个迭代过程中增加超过一个子节点。
Methods:
Problem setting.
完美信息的游戏,如:国际象棋,围棋等等,可以定义为:alternating Markov games。 在这些游戏中,有状态空间 S, 一个动作空间 A(s),一个转移函数 f(s, a, $\epison$),最终得到一个奖励函数 $r^i(s)$。我们限制了我们的注意力在 two-player zero-sum games, $r^1(s) = -r^2(s) = r(s)$,带有决定性的状态转移, $f(s, a, \epison) = f(s, a)$,在终止时间步骤 T 的时候奖赏为 0.
此处,补充一个知识,即:什么是“zero-sum game” ?
零和博弈又称零和游戏(Zero-sum game),与非零和博弈相对,是博弈论的一个概念,属非合作博弈,指参与博弈的各方,在严格竞争下,
一方的收益必然意味着另一方的损失,博弈各方的收益和损失相加总和永远为“零”。双方不存在合作的可能. 也可以说:自己的幸福是建立在他人的痛苦之上的,二者的大小完全相等,因而双方都想尽一切办法以实现“损人利己”。
Priori Work.
最优值函数 可以通过 minimax search 迭代的进行计算。大部分游戏都不适合进行充分的 minimax tree search;利用一个估计的值函数 $v(s) = v^*(s)$ 在游戏中去代替 terminal rewards。深度有限的 minimax search 和 alpha-beta pruning 已经在某些游戏上取得了超人的效果,但是在围棋上还不行。
RL 可以直接从 self-play 中去学习预测最优的 value function。之前的工作一直强调在一个线性的组合,即:feature 和 权重的组合。权重是利用 timporal-difference learning 在各种游戏中进行训练,或者利用线性回归。 Temporal-difference learning 也被用来训练一个神经网络来预测最优的 value function,在 backgammon 中取得了超人的效果。
另一个方法来解决 minimax search 的问题是:MCTS,通过一个 double approximation 来预测 interior nodes 的最优值,即:
$V^n(s) ≈ v^{p^n}(s) ≈ v^*(s)$。
第一个估计是:$V^n(s) ≈ v^{p^n}(s) $,利用 n 个 蒙特卡罗估计来预测一个模拟策略 $p^n$ 的 value function;
第二个估计是:$v^{p^n}(s) ≈ v^*(s)$,利用一个模拟策略 $p^n$ 来替换掉 minimax optimal actions。
这个模拟策略选择一个动作,根据一个搜索控制函数:
argmax_a (Q^n(s, a) + u(s, a)) ,
例如:UTC,选择具有较高 action value 的孩子节点,$Q^n(s, a) = -V^n(f(s, a))$,加上一个 bonus u(s, a) 来激励 exploration;或者在状态 s 下缺少搜索树的时候,它可以从一个快速的 rollout policy 来采样一个动作。随着尝试更多的模拟,这个搜索树变得越来越深,这个模拟策略就变得见识广泛,通过增加准确统计。在极限情况下,估计变得准确 MCTS 收敛到一个最优的 value function处,即:
目前最强的围棋程序都是基于 MCTS 的。
MCTS 在前人的工作中已经被用于缩小搜索范围(the beam of the tree)朝向可能性较高的 move 来执行;或者偏移 the bonus term。
AlphaGo 是基于截断的 MC 搜索算法来利用 value function,在游戏结束前终止 rollouts,并且利用 value function 来替换最终的奖赏。AlphaGo 的位置评价混合了 full rollouts 和 truncated rollouts,在某些角度是模仿了著名的 temporal-difference learning algorithm TD($\lambda$)。AlphaGo 也利用了较慢的 但非常有效的 policy 和 value function 的表示。
MCTS 的性能很大程度上依赖于 rollout policy 的质量。先前的工作集中于 手工设计的模式 或者通过监督学习,RL,simulation balance 或者 online adaption,进行 rollout policies 的学习。但是,基于 rollout 的位置估计是经常不准确的。AlphaGo 利用相对简单的 rollouts,直接利用 value networks 来解决比较有挑战性的位置评价问题。
Search Algorithm:
为了有效的融合神经网络到 AlphaGo当中,我们执行一个 asynchronous policy 和 value MCTS algorithm。搜索树中的每个节点 s 都包含边(s, a),以及所有的合法 action a。每一个 edge 都存贮一系列的 statics:
其中,P(s, a)是先验概率,$W_v(s, a), W_r(s, a)$ 是总action value 的蒙特卡罗估计,分别通过叶子评价 $N_v(s, a)$ 和 rollout rewards $N_r(s, a)$累计下来。 Q(s, a)是那个 edge 组合的平均 action value。在独立的搜索线程上并行的执行多个模拟操作。该算法大体上可以分为 4个阶段,就是如上文所示的那样,即:
Selection,Evaluation, Backup,Expansion。
搜索的结束阶段,AlphaGo 选择一个带有最大访问次数的 action;这比最大化 action value 对 outliers 的鲁棒性更强。搜索树在后续的时间步骤中仍然被用到:选择的action对应的孩子节点 变成了新的根节点;这个孩子节点下面的子树的所有统计保持不变,但是树的其余部分就被丢弃了。
Rollout Policy.
Rollout policy $p_{\pi}(a|s)$ 是基于快速,增量计算 的线性 softmax policy。