C++实现红黑树

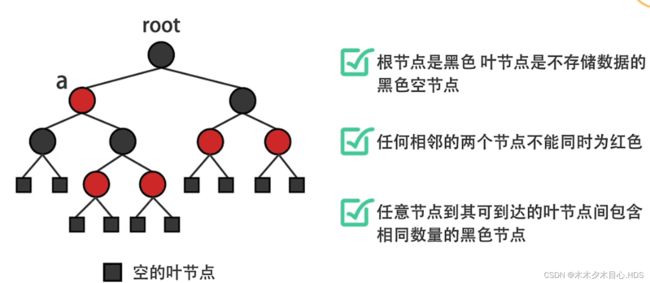
1.红黑树的基本概念

 2.节点的定义

// 基本定义
enum RBTColor{RED, BLACK};
template
class RBTNode{
public:
	RBTColor color; // 颜色
	T key; // 键值 
	RBTNode* left; // 左孩子
	RBTNode* right; // 右孩子
	RBTNode* parent; // 父节点
	RBTNode(T value, RBTColor c, RBTNode* p, RBTNode* l, RBTNode* r):
		key(value),color(c),parent(p),left(l),right(r){
	} 
};

3.红黑树类的定义

template
class RBTree{
private:
	RBTNode* mRoot;
public:
	RBTree();
	~RBTree();
	// 前序遍历
	void preOrder();
	// 中序遍历 
	void inOrder();
	// 后序遍历 
	void postOrder();
	RBTNode* iterativeSearch(T key);
	// (递归实现)查找”红黑树“中键值为key的节点
	RBTNode* search(T key); 
	// 查找最小节点：返回最小节点的键值
	T minimum();
	// 查找最大节点：返回最大节点的键值
	T maximum(); 
	// 将节点（key为节点键值）插入到红黑树中
	void insert(T key);
	// 删除节点（key为节点键值）
	void remove(T key);
	// 销毁红黑树
	void destroy();
	// 打印红黑树
	void print(); 
private:
	// 前序遍历”红黑树“
	void preOrder(RBTNode* tree) const;
	// 中序遍历”红黑树“ 
	void inOrder(RBTNode* tree) const;
	// 后续遍历“红黑树” 
	void postOrder(RBTNode* tree) const;
	// (递归实现)查找”红黑树“中键值为key的节点
	RBTNode* search(RBTNode* x ,T key) const;
	// (非递归实现)查找”红黑树“中键值为key的节点
	RBTNode* iterativeSearch(RBTNode* x ,T key) const;  
	// 查找最小节点：返回最小节点的键值
	RBTNode* minimum(RBTNode* tree);
	// 查找最大节点：返回最大节点的键值
	RBTNode* maximum(RBTNode* tree);
	// 查找节点(X)的后继节点，即查找在红黑树中大于该节点值的最小节点 
	RBTNode* successor(RBTNode* x); 
	// 查找节点(X)的前驱节点，即查找在红黑树中小于该节点值的最大节点 
	RBTNode* predecessor(RBTNode* x);   
	// 左旋
	void leftRotate(RBTNode* &root, RBTNode* x);
	// 右旋
	void rightRotate(RBTNode* &root, RBTNode* y);
	// 插入函数
	void insert(RBTNode*&root, RBTNode* node);
	// 插入修正函数
//	void insertFixUp(RBTNode*&root, RBTNode* node, RBTNode* parent);
	void insertFixUp(RBTNode*&root, RBTNode* node);
	// 删除的修正函数 
	void removeFixUp(RBTNode*&root, RBTNode* node, RBTNode* parent);
	// 查找需要替代删除的节点 
	RBTNode* findReplaceNode(RBTNode* node);
	// 销毁红黑树
	void destroy(RBTNode* &tree);
	// 打印红黑树
	void print(RBTNode* &tree, T key, int direction); 

#define rb_parent(r) ((r)->parent)
#define rb_color(r) ((r)->color)
#define rb_is_red(r) ((r)->color == RED)
#define rb_is_black(r) ((r)->color == BLACK)
#define rb_set_black(r) do{(r)->color = BLACK;}while(0)
#define rb_set_red(r) do{(r)->color = RED;}while(0)
#define rb_set_parent(r, p) do{(r)->parent=(p);}while(0)
#define rb_set_color(r,c) do{(r)->color = (c);}while(0)
};

4.红黑树中几个主要的算法解析

4.1前驱算法思路

查找节点(X)的前驱节点，即查找在红黑树中小于该节点值的最大节点 。

如上图所示，节点值为10的前驱应该是以其左孩子为根节点的子树中的最大值节点，即节点值为8。查找思路：若查找节点X的前驱，则先移动到X的左孩子(X->left)，再一直查找右孩子直到右孩子为空。

4.2后继算法思路

查找节点(X)的后继节点，即查找在红黑树中大于该节点值的最小节点 

如上图所示，节点值为10的后继节点应该是以其右孩子为根节点的子树中的最小值节点，即节点值为11。查找思路：若查找节点X的后继，则先移动到X的右孩子(X->right)，再一直查找左孩子直到左孩子为空。

4.3插入算法思路

（1）插入的节点若是根节点，则直接染黑

 （2）插入的节点X（不管是左孩子还是右孩子）的父节点P为黑色，则不用操作

（3）L为P的左孩子，若新插入的节点X的父节点L和叔叔节点R都是红色，则将L和R染黑，P染红，再将P作为新插入的节点继续向上判断 

 （4）L为P的左孩子，若插入的节点X的父节点L为红色且X为L的左孩子，叔叔节点R为黑色，则根据P右旋，将L染黑，P染红

（5）若插入节点X为父节点L的右孩子，且L为红色，叔叔节点R为黑色，则先根据L左转，再根据P右转，将X染黑，P染红

（6）R为P的右孩子，若插入的节点X的父节点R为红色且X为L的右孩子，叔叔节点L为黑色，则根据P左旋，将R染黑，P染红

（7）R为P的右节点，若插入节点X为父节点R的左孩子，且R为红色，叔叔节点L为黑色，则先根据R右转，再根据P左转，将X染黑，P染红

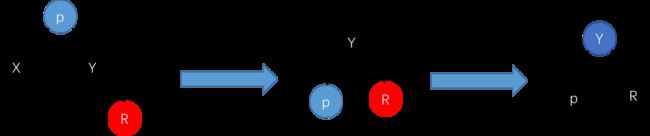
4.4删除算法思路

删除节点方案：

1.找到前驱节点，复制前驱节点值覆盖预备删除的节点的值，然后删除前驱节点

2.找到后继节点，复制后继节点值覆盖预备删除的节点的值，然后删除后继节点

通过前驱节点与后继节点的替换，可以将删除的节点转移到叶子节点上，方便操作

蓝色节点表示红或者黑，下面删除的节点都是以删除节点x为例

（1）删除节点x为红色，不管是父节点的左孩子还是右孩子，则直接删除

（2）删除的节点x为黑色，且其兄弟节点Y为叶节点且为黑色，则将x删除，p变为黑色，Y变为红色 

 （3）节点X与Y为黑色，且节点X的兄弟节点Y，只包含左孩子L且为红色，则删除节点X后，需要先根据Y右旋，再据P左旋，将L变为P的颜色，再将P染黑

 （4）节点X与Y为黑色，节点X的兄弟节点Y，只包含右孩子R且为红色，则删除节点X后，据P左旋，再将Y变为P的颜色，将P和R染黑。

 （5）节点X和其兄弟节点Y都为黑色，Y的左孩子与右孩子都为红色，将节点X删除，再根据P进行左旋，再将Y变为P的颜色，P和R变黑

​​​​

（6）被删除的节点X为黑色，其兄弟节点Y为红色，则Y的左孩子与右孩子比为黑色。删除节点X，在根据P进行左旋，再将Y染黑，L染红

4.5红黑树代码

有点大800行左右

#include
#include 
using namespace std;


/**
	1.节点红或者黑
	2. 根节点为黑色
	3.空叶节点为黑色
	4.红色节点的孩子是黑色
	5.从根节点出发到所以空叶节点的简单路径中黑色节点数量相等

	初始插入节点是红色
	1.插入位置为根，直接染黑
	2.父亲节点如果是黑色，则不需要染色或者旋转
	3.父亲节点是红色，叔叔节点也是红色。父亲和叔叔节点染成黑色，爷爷染成红色，
	  把爷爷看成新插入的节点，循环向上插入
	4.父亲节点是红色，叔叔节点是黑色。
		（1）当前节点是其父节点的左节点且父节点是祖父节点的左孩子，
			 则父节点右旋转，父节点变黑，祖父节点变红，父节点的右子树变为祖父节点的左子树。
		（2）当前节点是其父节点的右孩子且父节点是祖父节点的右孩子，
			 则父节点左旋，父节点变黑，祖父节点变红，父节点的左孩子变为祖父节点的右孩子。
	5. 父亲节点是红色，叔叔节点是黑色
		（1） 当前节点是其父节点的右节点且父节点是祖父节点的左节点，
			  则先以父节点进行左旋转，再以祖父节点右旋转【4.1】
		（2） 当前节点是父节点的左节点且父节点是祖父节点的右节点，
			  则先以父节点右旋转，再以祖父节点左旋转【4.2】



*/
// 基本定义
enum RBTColor { RED, BLACK };
template
class RBTNode {
public:
	RBTColor color; // 颜色
	T key; // 键值 
	RBTNode* left; // 左孩子
	RBTNode* right; // 右孩子
	RBTNode* parent; // 父节点
	RBTNode(T value, RBTColor c, RBTNode* p, RBTNode* l, RBTNode* r) :
		key(value), color(c), parent(p), left(l), right(r) {
	}
};

template
class RBTree {
private:
	RBTNode* mRoot;
public:
	RBTree();
	~RBTree();
	// 前序遍历
	void preOrder();
	// 中序遍历 
	void inOrder();
	// 后序遍历 
	void postOrder();
	RBTNode* iterativeSearch(T key);
	// (递归实现)查找”红黑树“中键值为key的节点
	RBTNode* search(T key);
	// 查找最小节点：返回最小节点的键值
	T minimum();
	// 查找最大节点：返回最大节点的键值
	T maximum();
	// 将节点（key为节点键值）插入到红黑树中
	void insert(T key);
	// 删除节点（key为节点键值）
	void remove(T key);
	// 销毁红黑树
	void destroy();
	// 打印红黑树
	void print();
private:
	// 前序遍历”红黑树“
	void preOrder(RBTNode* tree) const;
	// 中序遍历”红黑树“ 
	void inOrder(RBTNode* tree) const;
	// 后续遍历“红黑树” 
	void postOrder(RBTNode* tree) const;

	// (递归实现)查找”红黑树“中键值为key的节点
	RBTNode* search(RBTNode* x, T key) const;
	// (非递归实现)查找”红黑树“中键值为key的节点
	RBTNode* iterativeSearch(RBTNode* x, T key) const;

	// 查找最小节点：返回最小节点的键值
	RBTNode* minimum(RBTNode* tree);
	// 查找最大节点：返回最大节点的键值
	RBTNode* maximum(RBTNode* tree);

	// 查找节点(X)的后继节点，即查找在红黑树中大于该节点值的最小节点 
	RBTNode* successor(RBTNode* x);
	// 查找节点(X)的前驱节点，即查找在红黑树中小于该节点值的最大节点 
	RBTNode* predecessor(RBTNode* x);

	// 左旋
	void leftRotate(RBTNode*& root, RBTNode* x);
	// 右旋
	void rightRotate(RBTNode*& root, RBTNode* y);
	// 插入函数
	void insert(RBTNode*& root, RBTNode* node);
	// 插入修正函数
//	void insertFixUp(RBTNode*&root, RBTNode* node, RBTNode* parent);
	void insertFixUp(RBTNode*& root, RBTNode* node);
	// 删除的修正函数 
	void removeFixUp(RBTNode*& root, RBTNode* node, RBTNode* parent);
	// 查找需要替代删除的节点 
	RBTNode* findReplaceNode(RBTNode* node);
	// 查找需要替代的节点，真实的节点替代 
	RBTNode* findReplaceNode2(RBTNode*& root, RBTNode* node);
	RBTNode* exchange_node(RBTNode*& root, RBTNode* node1, RBTNode* node2);
	// 因插入或删除节点引起父节点与子节点为两个红色，造成错误的结构 
	void fixUpNode(RBTNode*& root, RBTNode* node);


	// 销毁红黑树
	void destroy(RBTNode*& tree);
	// 打印红黑树
	void print(RBTNode*& tree, T key, int direction);

#define rb_parent(r) ((r)->parent)
#define rb_color(r) ((r)->color)
#define rb_is_red(r) ((r)->color == RED)
#define rb_is_black(r) ((r)->color == BLACK)
#define rb_set_black(r) do{(r)->color = BLACK;}while(0)
#define rb_set_red(r) do{(r)->color = RED;}while(0)
#define rb_set_parent(r, p) do{(r)->parent=(p);}while(0)
#define rb_set_color(r,c) do{(r)->color = (c);}while(0)

};
/**
*构造函数
*/
template
RBTree::RBTree() :mRoot(NULL) {
	//mRoot = NULL;
}
/**
* 析构函数
*/
template
RBTree::~RBTree() {
	destroy();
}
/**
* 前序遍历”红黑树“
*/
template
void RBTree::preOrder(RBTNode* tree) const {
	if (tree != NULL) {
		cout << tree->key << " ";
		preOrder(tree->left);
		preOrder(tree->right);
	}
}
template
void RBTree::preOrder() {
	this->preOrder(mRoot);
}
/**
* 中序遍历”红黑树“
*/
template
void RBTree::inOrder(RBTNode* tree) const {
	if (tree != NULL) {
		inOrder(tree->left);
		cout << tree->key << " ";
		inOrder(tree->right);
	}
}
template
void RBTree::inOrder() {
	this->inOrder(mRoot);
}
/**
* 后序遍历”红黑树“
*/
template
void RBTree::postOrder(RBTNode* tree) const {
	if (tree != NULL) {
		postOrder(tree->left);
		postOrder(tree->right);
		cout << tree->key << " ";
	}
}
template
void RBTree::postOrder() {
	this->postOrder(mRoot);
}

/**
* (递归实现)查找”红黑树“中键值为key的节点
*/
template
RBTNode* RBTree::search(RBTNode* x, T key) const {
	if (x == NULL || x->key == key) {
		return x;
	}
	if (key < x->key) {
		return search(x->left, key);
	}
	else {
		return search(x->right, key);
	}
}
template
RBTNode* RBTree::search(T key) {
	return search(mRoot, key);
}
// (非递归实现)查找”红黑树“中键值为key的节点
template
RBTNode* RBTree::iterativeSearch(RBTNode* x, T key) const {
	while (x != NULL && x->key != key) {
		if (key < x->key) {
			return iterativeSearch(x->left, key);
		}
		else {
			return iterativeSearch(x->right, key);
		}
	}
	return x;
}
template
RBTNode* RBTree::iterativeSearch(T key) {
	return iterativeSearch(mRoot, key);
}
/**
* 查找最小节点：返回最小节点的键值
*/
template
RBTNode* RBTree::minimum(RBTNode* tree) {
	if (tree == NULL) {
		return NULL;
	}
	while (tree->left != NULL) {
		tree = tree->left;
	}
	return tree;
}
template
T RBTree::minimum() {
	RBTNode* p = minimum(mRoot);
	if (p != NULL) {
		return p->key;
	}
	return 0;
}
/**
* 查找最大节点：返回最大节点的键值
*/
template
RBTNode* RBTree::maximum(RBTNode* tree) {
	if (tree == NULL) {
		return NULL;
	}
	while (tree->right != NULL) {
		tree = tree->right;
	}
	return tree;
}
template
T RBTree::maximum() {
	RBTNode* p = maximum(mRoot);
	if (p != NULL) {
		return p->key;
	}
	return 0;
}

/**
* 查找节点(X)的后继节点，即查找在红黑树中大于该节点值的最小节点
*/
template
RBTNode* RBTree::successor(RBTNode* x) {
	// 如果x存在右孩子，则x的后继节点为其右孩子作为根节点子树的最小节点
	if (x->right != NULL) {
		return minimum(x->right);
	}
	// 如果x没有右孩子，则x有一下两种可能
	// 1.x是父节点的左孩子，则x的后继节点为父节点
	// 2.x是父节点的右孩子，则需要循环查找x的最低父节点，并且该父节点具有左孩子 
	RBTNode* y = x->parent;
	while (y != NULL && x != y->left) {
		x = y;
		y = y->parent;
	}
	return y;
}
/**
* 查找节点(X)的前驱节点，即查找在红黑树中小于该节点值的最大节点
*/
template
RBTNode* RBTree::predecessor(RBTNode* x) {
	// 如果x存在左孩子，则x的后继节点为其右孩子作为根节点子树的最大节点
	if (x->left != NULL) {
		return maximum(x->left);
	}
	// 如果x没有左孩子，则x有一下两种可能
	// 1.x是父节点的右孩子，则x的后继节点为父节点
	// 2.x是父节点的左孩子，则需要循环查找x的最低父节点，并且该父节点具有右孩子 
	RBTNode* y = x->parent;
	while (y != NULL && x != y->right) {
		x = y;
		y = y->parent;
	}
	return y;
}

/**
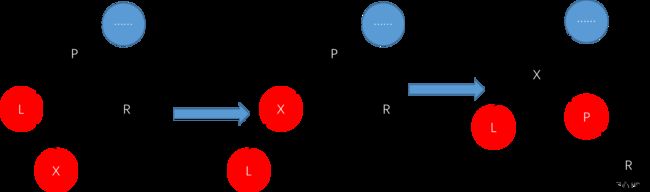
左旋
		 px											px
		/	         对x进行左旋转                 /
	   x             ------------>                y
	  / \										 / \
	 lx  y                                      x   ry
		/ \ 								   / \
	   ly  ry								  lx  ly
*/

template
void RBTree::leftRotate(RBTNode*& root, RBTNode* x) {
	// 设置x的右孩子y
	RBTNode* y = x->right;
	// 将y的左孩子设为x的右孩子
	// 如果y的左孩子非空，将x设为y的左孩子的父亲
	x->right = y->left;
	if (y->left != NULL) {
		y->left->parent = x;
	}
	// 将x的父节点设置为y的父节点
	y->parent = x->parent;
	if (x->parent == NULL) {
		root = y; // 如果x的父节点为空，则将y设为根节点 
	}
	else {
		if (x->parent->left == x) {
			x->parent->left = y; // 如果x是他父节点的左孩子，则将y设为x的父节点的左孩子 
		}
		else {
			x->parent->right = y;// 如果x是他父节点的右孩子，则将y设为x的父节点的右孩子 
		}
	}
	// 将x设为y的左孩子
	y->left = x;
	// 将x的父节点设为y
	x->parent = y;
}
/**
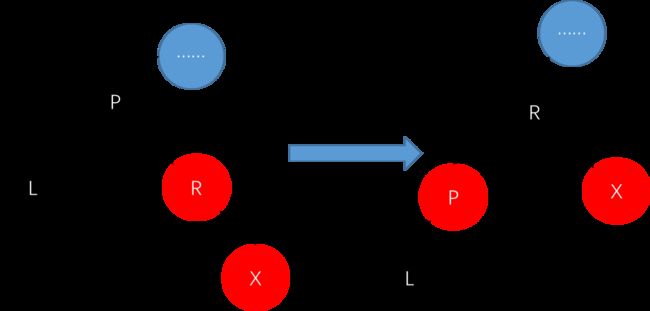
右旋转
			py 								py
		   /							   /
		  y								  x
		 / \	  对y进行右旋转 		 / \
		x   ry    ------------>     	lx  y
	   / \								   / \
	  lx  rx							  rx  ry
*/
template
void RBTree::rightRotate(RBTNode*& root, RBTNode* y) {
	// 获取节点x 
	RBTNode* x = y->left;
	// 如果x的右孩子非空,则将x的右孩子设置为y的左孩子
	y->left = x->right;
	if (x->right != NULL) {
		x->right->parent = y;
	}
	// 将x的父节点指向y的父节点 
	x->parent = y->parent;
	if (y->parent == NULL) {
		root = x; // 如果y为根节点，则将x变为新的根节点 
	}
	else {
		if (y->parent->left == y) {
			y->parent->left = x; // 如果y为父节点的左孩子，则将x设置为父节点的左孩子 
		}
		else {
			y->parent->right = x; // 如果y为父节点的右孩子，则将x设置为父节点的右孩子 
		}
	}
	y->parent = x; // 将y的父节点设置为x
	x->right = y;  // 将x的右孩子设置为y 	
}

/**
红黑树插入修正函数
在向红黑树中插入节点之后（失去平衡），再调用该函数 ；
目的是将它重新塑造成一颗红黑树
参数说明：
	root 红黑树的根
	node 插入的节点
*/
//#define rb_parent(r) ((r)->parent)
//#define rb_color(r) ((r)->color)
//#define rb_is_red(r) ((r)->color == RED)
//#define rb_is_black(r) ((r)->color == BLACK)
//#define rb_set_black(r) do{(r)->color = BLACK;}while(0)
//#define rb_set_red(r) do{(r)->color = RED;}while(0)
//#define rb_set_parent(r, p) do{(r)->parent=(p);}while(0)
//#define rb_set_color(r,c) do{(r)->color = (c);}while(0)
/**
	初始插入节点是红色
	1.插入位置为根，直接染黑
	2.父亲节点如果是黑色，则不需要染色或者旋转
	3.父亲节点是红色，叔叔节点也是红色。父亲和叔叔节点染成黑色，爷爷染成红色，
	  把爷爷看成新插入的节点，循环向上插入
	4.父亲节点是红色，叔叔节点是黑色。
		（1）当前节点是其父节点的左节点且父节点是祖父节点的左孩子，
			 则父节点右旋转，父节点变黑，祖父节点变红，父节点的右子树变为祖父节点的左子树。
		（2）当前节点是其父节点的右孩子且父节点是祖父节点的右孩子，
			 则父节点左旋，父节点变黑，祖父节点变红，父节点的左孩子变为祖父节点的右孩子。
	5. 父亲节点是红色，叔叔节点是黑色
		（1） 当前节点是其父节点的右节点且父节点是祖父节点的左节点，
			  则先以父节点进行左旋转，再以祖父节点右旋转【4.1】
		（2） 当前节点是父节点的左节点且父节点是祖父节点的右节点，
			  则先以父节点右旋转，再以祖父节点左旋转【4.2】
*/
template
void RBTree::insertFixUp(RBTNode*& root, RBTNode* node) {
	// 定义父节点和祖父节点 
	RBTNode* parent;
	RBTNode* gparent;
	RBTNode* uncle;
	parent = rb_parent(node);
	// 1.插入位置为根，直接染黑
	if (parent == NULL) {
		rb_set_black(node);
		root = node;
		return;
	}
	// 2.父亲节点如果是黑色，则不需要染色或者旋转
	if (rb_is_black(parent)) {
		return;
	}
	RBTNode* curNode = node;
	parent = rb_parent(curNode);
	while (parent != NULL && rb_is_red(parent)) {
		gparent = rb_parent(parent);
		// 先讨论父节点是祖父节点左孩子的情况 
		if (parent == gparent->left) {
			uncle = gparent->right;
			if (uncle == NULL || rb_is_black(uncle)) {
				if (curNode == parent->right) {
					// 5.若插入节点为父节点的右孩子，且父节点为红色，叔叔节点为黑色，
					// 则先根据父节点左转，（再根据祖父右转，将当前染黑，祖父染红）跳转到4 	
					leftRotate(root, parent);
					curNode = parent;
					parent = rb_parent(curNode);
				}
				if (curNode == parent->left) {
					// 4.父节点为祖父节点的左孩子，若插入的节点的父节点为红色且为父节点的左孩子，叔叔节点为黑色，
					// 则根据祖父节点右旋，将父节点染黑，祖父染红
					rightRotate(root, gparent);
					rb_set_black(parent); // 将父节点染黑 
					rb_set_red(gparent);  // 将祖父节点染红 
					break;
				}
			}
		}// 父节点是祖父节点右孩子的情况 
		else {
			uncle = gparent->left;
			if (uncle == NULL || rb_is_black(uncle)) {
				if (curNode == parent->left) {
					// 7.父节点为祖父节点的右孩子，若插入节点为父节点的左孩子，且父节点为红色，叔叔节点为黑色，
					// 则先根据父节点右转，（再根据祖父左转，将当前染黑，祖父染红）跳转到6
					rightRotate(root, parent);
					curNode = parent;
					parent = rb_parent(curNode);
				}
				if (curNode == parent->right) {
					// 6.父节点为祖父节点的右孩子，若父节点为红色且插入节点为父节点的右孩子，叔叔节点为黑色，
					//则根据祖父左旋，将父节点染黑，祖父染红
					leftRotate(root, gparent);
					rb_set_black(parent); // 将父节点染黑 
					rb_set_red(gparent);  // 将祖父节点染红 
					break;
				}
			}
		}
		//3.父亲节点是红色，叔叔节点也是红色。父亲和叔叔节点染成黑色，
		//  爷爷染成红色，把爷爷看成新插入的节点，循环向上插入 
		if (uncle != NULL && rb_is_red(uncle)) {
			rb_set_black(parent); // 将父节点染黑 
			rb_set_black(uncle);  // 将叔叔节点染黑 
			rb_set_red(gparent);  // 将祖父节点染红 
			curNode = gparent;
			parent = rb_parent(curNode);
		}
	}
	// 将根节点设为黑色
	rb_set_black(root);
}
// 插入函数
/**
* 将节点插入到红黑树中
* root : 红黑树的根节点
* node : 插入的节点
*/
template
void RBTree::insert(RBTNode*& root, RBTNode* node) {
	RBTNode* y = NULL;
	RBTNode* x = root;
	node->left = NULL;
	node->right = NULL;
	// 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉树中
	while (x != NULL) {
		y = x;
		if (node->key < x->key) {
			x = x->left;
		}
		else {
			x = x->right;
		}
	}
	node->parent = y;
	if (y != NULL) {
		if (node->key < y->key) {
			y->left = node;
		}
		else {
			y->right = node;
		}
	}
	else {
		root = node;
	}
	// 2.设置节点的颜色为红色
	node->color = RED;
	// 3.将它重新修正为一颗红黑树
	insertFixUp(root, node);
}
/**
* 将节点（key为节点键值）插入到红黑树中
* 参数说明
* key ：插入点的键值
*/
template
void RBTree::insert(T key) {
	RBTNode* z = NULL;
	// 如果新建节点失败，则返回
	if ((z = new RBTNode(key, RED, NULL, NULL, NULL)) == NULL) {
		return;
	}
	insert(mRoot, z);
}
/**
 红黑树删除修正函数
 在从红黑树中删除插入节点之后（红黑树失去平衡），再调用该函数，目的是将它重新塑造成一颗红黑树
 参数说明：
 root : 红黑树的根
 node : 待修正的节点

删除操作：
主题思想是：若删除的节点不是叶子节点，则可以查找该节点的后继节点的值将其代替，再删除替代它的节点，因为后继节点一般是叶节点，
			则删除操作可以简化为对叶节点进行操作。
	1.叶节点是红色，直接删除
	2.
*/

// 查找需要替代删除的节点 ,叶子节点即可 
template
RBTNode* RBTree::findReplaceNode(RBTNode* node) {
	// 1.node本身就是叶子节点
	// 2.node存在左孩子或者右孩子
	RBTNode* curNode = node;
	RBTNode* preNode = node;
	while (curNode->left != NULL || curNode->right != NULL) {
		// 先找后继节点 
		if (curNode->right != NULL) {
			curNode = this->successor(curNode);
		}
		preNode->key = curNode->key;
		preNode = curNode;
		// 查找前驱节点 
		if (curNode->left != NULL) {
			curNode = this->predecessor(curNode);
		}
		preNode->key = curNode->key;
		preNode = curNode;
	}
	return curNode;
}
/**
* 交换两个节点
*/
template
RBTNode* RBTree::exchange_node(RBTNode*& root, RBTNode* preNode, RBTNode* curNode) {
	RBTNode* cur_p = NULL;
	RBTNode* cur_l = NULL;
	RBTNode* cur_r = NULL;
	RBTColor cur_rb;
	RBTNode* pre_p = NULL;
	RBTNode* pre_l = NULL;
	RBTNode* pre_r = NULL;
	RBTColor pre_rb;

	cur_p = curNode->parent;
	cur_l = curNode->left;
	cur_r = curNode->right;
	cur_rb = curNode->color;
	pre_p = preNode->parent;
	pre_l = preNode->left;
	pre_r = preNode->right;
	pre_rb = preNode->color;

	curNode->parent = pre_p;
	if (pre_p == NULL) {
		root = curNode;
	}else{
		if (pre_p->left == preNode) {
			pre_p->left = curNode;
		}
		else {
			pre_p->right = curNode;
		}
	}
	// 1.curNode是preNode的子节点
	if (cur_p == preNode) {
		preNode->parent = curNode;
		preNode->left = cur_l;
		preNode->right = cur_r;
		if (preNode->left == curNode) {
			curNode->left = preNode;
			curNode->right = pre_r;
		}
		else
		{
			curNode->right = preNode;
			curNode->left = pre_l;
		}
	}// 2.curNode不是preNode的子节点
	else {
		// curNode节点的左孩子
		curNode->left = pre_l;
		if (pre_l != NULL) {
			pre_l->parent = curNode;
		}
		// curNode节点的右孩子
		curNode->right = pre_r;
		if (pre_r != NULL) {
			pre_r->parent = curNode;
		}
		// preNode节点的父节点
		preNode->parent = cur_p;
		if (cur_p->left == curNode) {
			cur_p->left = preNode;
		}
		else {
			cur_p->right = preNode;
		}
		// preNode节点的左孩子
		preNode->left = cur_l;
		if (cur_l != NULL) {
			cur_l->parent = preNode;
		}
		// preNode节点的右孩子
		preNode->right = cur_r;
		if (cur_r != NULL) {
			cur_r->parent = preNode;
		}
	}
	curNode->color = pre_rb;
	preNode->color = cur_rb;
	return preNode;
}

// 查找需要替代的节点，真实的节点替代 
template
RBTNode* RBTree::findReplaceNode2(RBTNode*& root, RBTNode* node) {
	// 1.node本身就是叶子节点
	// 2.node存在左孩子或者右孩子
	RBTNode* curNode = node;
	RBTNode* preNode = node;
	RBTNode* p = NULL;
	RBTNode* l = NULL;
	RBTNode* r = NULL;
	RBTNode* preParent = NULL;
	RBTColor rb;
	while (curNode->left != NULL || curNode->right != NULL) {
		// 先找后继节点 
		if (curNode->right != NULL) {
			curNode = this->successor(curNode);
		}
		if (curNode != preNode) {
			curNode = exchange_node(root, preNode, curNode);
		}
		// 查找前驱节点 
		if (curNode->left != NULL) {
			curNode = this->predecessor(curNode);
		}
		if (curNode != preNode) {
			curNode = exchange_node(root, preNode, curNode);
		}
	}
	return curNode;
}

// 因插入或删除节点引起父节点与子节点为两个红色，造成错误的结构 
template
void RBTree::fixUpNode(RBTNode*& root, RBTNode* node) {
	if (node != NULL) {
		fixUpNode(root, node->left);
		fixUpNode(root, node->right);
		this->insert(root, node);
	}
}

//#define rb_parent(r) ((r)->parent)
//#define rb_color(r) ((r)->color)
//#define rb_is_red(r) ((r)->color == RED)
//#define rb_is_black(r) ((r)->color == BLACK)
//#define rb_set_black(r) do{(r)->color = BLACK;}while(0)
//#define rb_set_red(r) do{(r)->color = RED;}while(0)
//#define rb_set_parent(r, p) do{(r)->parent=(p);}while(0)
//#define rb_set_color(r,c) do{(r)->color = (c);}while(0)

template
void RBTree::removeFixUp(RBTNode*& root, RBTNode* node, RBTNode* parent) {
	RBTNode* x = this->findReplaceNode2(root, node); // 将删除的节点转移到叶子节点 
//	RBTNode* x = this->findReplaceNode(node); // 将删除的节点转移到叶子节点 
	RBTNode* p = rb_parent(x);
	RBTNode* y = NULL;
	RBTNode* l = NULL;
	RBTNode* r = NULL;
	// 判断是否删除最后一个节点了 
	if (p == NULL) {
		delete x;
		root = NULL;
		return;
	}
	// 先判断删除的叶子节点为父节点的左孩子情况 
	if (x == p->left) {
		y = p->right; // x的兄弟节点
		if (y != NULL) {
			l = y->left;
			r = y->right;
		}
		// 删除的节点为黑色节点 
		if (rb_is_black(x)) {
			p->left = NULL;
			delete x;
			// X的兄弟节点y为黑色 
			if (rb_is_black(y)) {
				// 2.删除的节点x为黑色，且其兄弟节点Y为叶节点且为黑色，则将x删除，p变为黑色，Y变为红色
				if (l == NULL && r == NULL) {
					rb_set_black(p);
					rb_set_red(y);
				}
				else if (l != NULL && rb_is_red(l) && r == NULL) {
					// 3.节点x与Y为黑色，节点X的兄弟节点Y，只包含左孩子L且为红色，则删除节点X后，
					// 需要先根据Y右旋，再据P左旋，将L变为P的颜色，再将P染黑
					rightRotate(root, y); // 根据y右旋
					leftRotate(root, p); // 根据p左旋
					l->color = p->color;
					rb_set_black(p);
				}
				else if (l == NULL && r != NULL && rb_is_red(r)) {
					//  4.节点X与Y为黑色，节点X的兄弟节点Y，只包含右孩子R且为红色，
					// 则删除节点X后，据P左旋，再将Y变为P的颜色，将P和R染黑。
					leftRotate(root, p); // 根据p左旋
					y->color = p->color;
					rb_set_black(p);
					rb_set_black(r);
				}
				else if (l != NULL && r != NULL && rb_is_red(r) && rb_is_red(l)) {
					// 5.节点X和其兄弟节点Y都为黑色，Y的左孩子与右孩子都为红色，
					// 将节点X删除，再根据P进行左旋，再将Y变为P的颜色，P和R变黑
					leftRotate(root, p); // 根据p左旋
					y->color = p->color;
					rb_set_black(p);
					rb_set_black(r);
				}
			}
			else {
				// 6. 被删除的节点X为黑色，其兄弟节点Y为红色，则Y的左孩子与右孩子为黑色。
				// 删除节点X，在根据P进行左旋，再将Y染黑，L染红
				if (l != NULL && r != NULL && rb_is_black(r) && rb_is_black(l)) {
					leftRotate(root, p); // 根据p左旋
					rb_set_black(y);
					rb_set_red(l);
					l->left = NULL;
					l->right = NULL;
					fixUpNode(root, l->left);
					fixUpNode(root, l->right);
				}
			}
		}
		else {
			// 1. 删除节点为红色，不管是父节点的左孩子还是右孩子，则直接删除
			p->left = NULL;
			delete x;
		}
	}// 再判断删除的叶子节点为父节点的右孩子情况 
	else {
		y = p->left; // x的兄弟节点
		if (y != NULL) {
			l = y->left;
			r = y->right;
		}
		// 删除的节点为黑色节点 
		if (rb_is_black(x)) {
			p->right = NULL;
			delete x;
			// X的兄弟节点y为黑色 
			if (rb_is_black(y)) {
				// 2.删除的节点x为黑色，且其兄弟节点Y为叶节点且为黑色，则将x删除，p变为黑色，Y变为红色
				if (l == NULL && r == NULL) {
					rb_set_black(p);
					rb_set_red(y);
				}
				else if (l != NULL && rb_is_red(l) && r == NULL) {
					// 3.节点x与Y为黑色，节点X的兄弟节点Y，只包含左孩子L且为红色，则删除节点X后，
					// P右旋，将Y变为P的颜色，P和L染黑 
					rightRotate(root, p); // 根据p右旋
					y->color = p->color;
					rb_set_black(p);
					rb_set_black(l);
				}
				else if (l == NULL && r != NULL && rb_is_red(r)) {
					//4. 节点X为父节点的右节点，节点X与Y为黑色，且节点X的兄弟节点Y只包含右孩子R且为红色，
					//则删除节点X后，需要先根据Y左旋，再据P右旋，将R变为P的颜色，再将P染黑
					leftRotate(root, y); // 根据p左旋
					rightRotate(root, p); // 根据p左旋
					r->color = p->color;
					rb_set_black(p);
				}
				else if (l != NULL && r != NULL && rb_is_red(r) && rb_is_red(l)) {
					// 5.节点X为父节点的右节点，节点X和其兄弟节点Y都为黑色，Y的左孩子与右孩子都为红色，将节点X删除，
					// 再根据P进行右旋，再将Y变为P的颜色，P和L变黑
					rightRotate(root, p); // 根据p左旋
					y->color = p->color;
					rb_set_black(p);
					rb_set_black(l);
				}
			}
			else {
				// 6.节点X为父节点的右孩子，被删除的节点X为黑色，其兄弟节点Y为红色，则Y的左孩子与右孩子为黑色。
				// 删除节点X，在根据P进行右旋，再将Y染黑，R染红
				if (l != NULL && r != NULL && rb_is_black(r) && rb_is_black(l)) {
					rightRotate(root, p); // 根据p左旋
					rb_set_black(y);
					rb_set_red(r);
					r->left = NULL;
					r->right = NULL;
					fixUpNode(root, r->left);
					fixUpNode(root, r->right);
				}
			}
		}
		else {
			// 1. 删除节点为红色，不管是父节点的左孩子还是右孩子，则直接删除
			p->right = NULL;
			delete x;
		}
	}
}
// 删除节点（key为节点键值）
template
void RBTree::remove(T key) {
	RBTNode* node;
	// 查找key对应的节点node，找到的话就删除该节点
	if ((node = search(mRoot, key)) != NULL) {
		removeFixUp(mRoot, node, NULL);
	}
}
/**
* 销毁红黑树
*/
template
void RBTree::destroy(RBTNode*& tree) {
	if (tree == NULL) {
		return;
	}
	destroy(tree->left);
	destroy(tree->right);
	delete tree;
	tree = NULL;
}
template
void RBTree::destroy() {
	destroy(mRoot);
}
/**
* 打印二叉查找树
 key 节点的键值
 direction    0 表示该节点是根节点
			  -1 表示该节点是它的父节点的左孩子
			  1  表示该节点是它父节点的右孩子
*/
template
void RBTree::print(RBTNode*& tree, T key, int direction) {
	if (tree != NULL) {
		if (direction == 0) { // tree是根节点 
			cout << setw(2) << tree->key << "(B) is root" << endl;
		}
		else {
			cout << setw(2) << tree->key << (rb_is_red(tree) ? "(R)" : "(B)") << " is " << setw(2) << key
				<< " 's " << setw(12) << (direction == 1 ? "right child" : "left child") << endl;
		}
		print(tree->left, tree->key, -1);
		print(tree->right, tree->key, 1);
	}
}
template
void RBTree::print() {
	if (mRoot != NULL) {
		print(mRoot, mRoot->key, 0);
	}
}
int main() {
	//	cout << "hello1111" << endl; 
	int a[] = { 10, 40, 30, 60, 90, 70, 20, 50, 80 };
	int check_insert = 0; // “插入”动作的检测开关（0，关闭；1，打开）
	int check_remove = 0; // “删除”动作的检测开关（0，关闭；1，打开）
	int i;
	int len = (sizeof(a)) / sizeof(a[0]);
	RBTree* tree = new RBTree();
	cout << "====原始数据：";
	for (i = 0; i < len; i++) {
		cout << a[i] << " ";
	}
	cout << endl;
	for (i = 0; i < len; i++) {
		tree->insert(a[i]);
		// 设置check_insert=1，测试“添加函数”
		if (check_insert) {
			cout << "==添加节点：" << a[i] << endl;
			cout << "==树的详细信息：" << endl;
			tree->print();
			cout << endl;
		}
	}
	cout << "==前序遍历：";
	tree->preOrder();
	cout << endl;
	cout << "==中序遍历：";
	tree->inOrder();
	cout << endl;
	cout << "==后序遍历：";
	tree->postOrder();
	cout << endl;
	cout << "==最小值：" << tree->minimum() << endl;
	cout << "==最大值：" << tree->maximum() << endl;
	cout << "==树的详细信息：" << endl;
	tree->print();
	cout << endl;
	// 设置check_remove = 1，测试“删除函数”
	check_remove = 1;
	if (check_remove) {
		for (i = 0; i < len; i++) {
			tree->remove(a[i]);
			cout << "==删除节点：" << a[i] << endl;
			cout << "==树的详细s信息：" << endl;
			tree->print();
			cout << endl;
		}
	}
//	int b = 0;
//	b = 10;
//	tree->remove(b);
//	b = 40;
//	tree->remove(b);
//	b = 30;
//	cout << "==删除节点：" << b << endl;
//	cout << "==树的详细信息：" << endl;
//	tree->remove(b);
//	tree->print();
//	cout << endl;
	// 销毁红黑树
	tree->destroy();
	return 0;
}

在删除操作那儿，后续还要再改动下