蓝桥杯2022第十三届—推导部分和(带权并查集的应用)
时间限制: 1Sec 内存限制: 256MB 提交: 174 解决: 26
题目描述
对于一个长度为 N 的整数数列 A1, A2, · · · AN,小蓝想知道下标 l 到 r 的部分和
![]()
是多少?
然而,小蓝并不知道数列中每个数的值是多少,他只知道它的 M 个部分和的值。其中第 i 个部分和是下标 li 到 ri 的部分和
![]()
,值是 S i 。
输入
第一行包含 3 个整数 N、M 和 Q。分别代表数组长度、已知的部分和数量和询问的部分和数量。
接下来 M 行,每行包含 3 个整数 li ,ri , S i。
接下来 Q 行,每行包含 2 个整数 l 和 r ,代表一个小蓝想知道的部分和。
输出
对于每个询问,输出一行包含一个整数表示答案。如果答案无法确定,输出 UNKNOWN。
样例输入复制
5 3 3 1 5 15 4 5 9 2 3 5 1 5 1 3 1 2
样例输出复制
15 6 UNKNOWN
提示
对于 10% 的评测用例,1 ≤ N, M, Q ≤ 10,−100 ≤ S i ≤ 100。
对于 20% 的评测用例,1 ≤ N, M, Q ≤ 20,−1000 ≤ S i ≤ 1000。
对于 30% 的评测用例,1 ≤ N, M, Q ≤ 50,−10000 ≤ S i ≤ 10000。
对于 40% 的评测用例,1 ≤ N, M, Q ≤ 1000,−106 ≤ S i ≤ 106。
对于 60% 的评测用例,1 ≤ N, M, Q ≤ 10000,−109 ≤ S i ≤ 109。
对于所有评测用例,1 ≤ N, M, Q ≤ 105,−1012 ≤ S i ≤ 1012,1 ≤ li ≤ ri ≤ N, 1 ≤ l ≤ r ≤ N。数据保证没有矛盾。
带权并查集的引入:
首先,需要了解并查集是什么,并查集主要描述的是集合与集合之间的关系,即某两个节点是否在同一个集合,具体可查看java实现并查集(模板)_霜见贰叁的博客-CSDN博客_java并查集模板。
然而,带权并查集不仅可以描述集合之间的关系,而且还描述了节点与节点之间的关系,即节点与节点之间的关系用权值来表示。在带权并查集中,核心的两个操作为:
- 路径压缩操作:查找节点x的根节点同时,压缩x到根节点的路径,使下一次查找x的根节点时,只需要O(1)时间复杂度就可以找到x的根节点;除此之外,还需要更新权值。
- 合并操作:合并时,不只是单纯将节点x的根节点xBoot与节点y的根节点yBoot连接起来,还需要更新xBoot到yBoot的权值。
路径压缩图解:
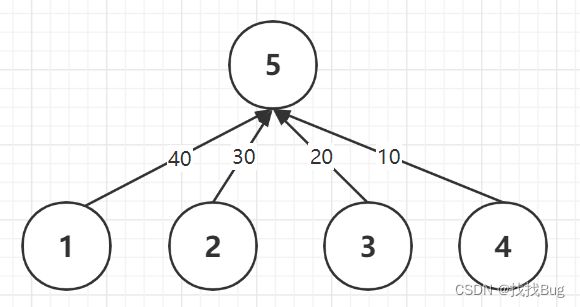
查找节点1和节点3的根节点5时,会产生路径压缩和权值更新。
压缩前:
压缩后:可以清楚地看到,每个节点都直接连接到了根节点5,且权值都更新为【从节点i到根节点root的路径权值和】。
当存在上面的连通图时,如果要查询节点1,2,3,4,5之间的权值,就可以轻易计算得出。比如:查询1到2的权值,结果为【1到5的权值40】减去【2到5的权值30】,等于10。
路径压缩代码:
// 查找;路径压缩
static int findFather(int x, int[] father, long[] value) {
if (x != father[x]) {
int temp = father[x];
father[x] = findFather(father[x], father, value);// 找根节点
value[x] += value[temp];// 压缩路径
}
return father[x];
}合并图解:
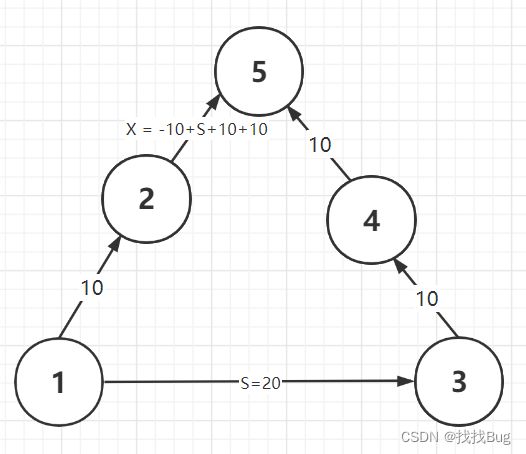
将节点1所在的集合(连通图)与节点3所在的集合(连通图)合并,其中S是1到3的权值。
合并时,将2指向5,且由于【1->2->5】路径的权值和与【1->3->4->5】路径的权值和相等,所以【2->5】的权值为X = -10 + S + 10 + 10。
合并代码:
// 找根节点,并压缩路径
int l_Father = findFather(l, father, value);
int r_Father = findFather(r, father, value);
if (l_Father != r_Father) {
// 合并l和r的集合,并更新权值
// 合并规则,将小根节点集合指向大根节点集合
int small = l_Father > r_Father ? r_Father : l_Father;
int big = small == r_Father ? l_Father : r_Father;
father[small] = big;
value[small] = Math.abs(-value[l] + value[r] + s);
}在本题中,想要求任意范围内的部分和时,只要左端点l和右端点r的根节点root相同,则利用【l到root的权值】减去【r到root的权值】就可以得出【l到r的权值】。由于本题中需要包括端点的值,因此节点序号从0开始,比如:求[1,5]区间的数字之和时,1到5之间只有4条边,只能求出四个位置上数的和,因此将求[1,5]区间的数字之和改为求(0,5]区间的数字和即可解决。
具体代码如下:
import java.util.Scanner;
/**
* 推导部分和,利用带权并查集求部分和
*
* @author hedingqin
*
*/
public class PartialSum {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int M = in.nextInt();
int Q = in.nextInt();
int[] father = new int[N + 1];// 每个节点的父节点
for (int i = 0; i <= N; i++) {
father[i] = i;
}
// value[i]表示i到其根节点的路径长度
// 本题中,左区间从0开始,计算部分和时不包括左端点的值。
// 原因:求1到2位置上的部分和时,若并查集结构为(1->2),此时1到2之间就只能
// 有一个权值,即只能知道1或者2位置上的值,所以并查集结构应改为(0->1->2),
// 即(0->1)的边权值表示1位置的值,(1->2)的边权值表示2位置的值,此时求1到2位置
// 上数字和时,即(0->1->2)路径的权值和。
long[] value = new long[N + 1];
while (M > 0) {
int l = in.nextInt();
int r = in.nextInt();
long s = in.nextLong();
l--;
// 找根节点,并压缩路径
int l_Father = findFather(l, father, value);
int r_Father = findFather(r, father, value);
if (l_Father != r_Father) {
// 合并l和r的集合,并更新权值
// 合并规则,将小根节点集合指向大根节点集合
int small = l_Father > r_Father ? r_Father : l_Father;
int big = small == r_Father ? l_Father : r_Father;
father[small] = big;
value[small] = Math.abs(-value[l] + value[r] + s);
}
M--;
}
while (Q > 0) {
int l = in.nextInt();
int r = in.nextInt();
l--;
int l_Father = findFather(l, father, value);
int r_Father = findFather(r, father, value);
// 同一集合,就能计算出其结果
if (l_Father == r_Father) {
System.out.println(value[l] - value[r]);
} else {
System.out.println("UNKNOWN");
}
Q--;
}
}
// 查找;路径压缩
static int findFather(int x, int[] father, long[] value) {
if (x != father[x]) {
int temp = father[x];
father[x] = findFather(father[x], father, value);// 找根节点
value[x] += value[temp];// 压缩路径
}
return father[x];
}
}