【LeetCode每日一题合集】2023.9.18-2023.9.24（⭐拓扑排序&⭐设计数据结构:LRU缓存实现 LinkedHashMap⭐）

337. 打家劫舍 III（树形DP）

https://leetcode.cn/problems/house-robber-iii/description/?envType=daily-question&envId=2023-09-18

提示：
树的节点数在 [1, 10^4] 范围内
0 <= Node.val <= 10^4

class Solution {
    public int rob(TreeNode root) {
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }

    public int[] dfs(TreeNode root) {
        // 返回值{a,b} a表示没选当前节点的最大值,b表示选了当前节点的最大值
        if (root == null) return new int[]{0, 0};
        int[] l = dfs(root.left), r = dfs(root.right);
        int a = Math.max(l[0], l[1]) + Math.max(r[0], r[1]), b = root.val + l[0] + r[0];
        return new int[]{a, b};
    }
}

2560. 打家劫舍 IV（二分查找+动态规划）

https://leetcode.cn/problems/house-robber-iv/description/?envType=daily-question&envId=2023-09-19

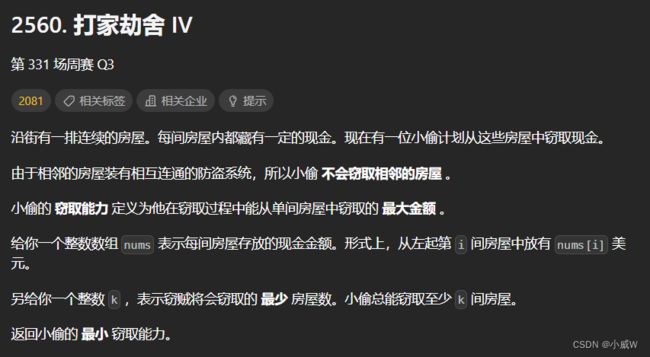
提示：
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
1 <= k <= (nums.length + 1)/2

二分查找答案。 对于每次查找，判断是否可以至少偷k家。

class Solution {
    public int minCapability(int[] nums, int k) {
        if (nums.length == 1) return nums[0];
        int l = Integer.MAX_VALUE, r = Integer.MIN_VALUE;
        for (int x: nums) {
            l = Math.min(l, x);
            r = Math.max(r, x);
        }
        // 二分查找答案
        while (l < r) {
            int mid = l + r >> 1;
            if (op(nums, mid) >= k) r = mid;
            else l = mid + 1;
        }
        return l;
    }

    // 动态规划
    public int op(int[] nums, int k) {
        int n = nums.length;
        int[] dp = new int[n];      // dp[i]表示0~i中最多能偷几个
        dp[0] = nums[0] <= k? 1: 0;
        dp[1] = Math.max(dp[0], nums[1] <= k? 1: 0);
        for (int i = 2; i < n; ++i) {
            dp[i] = Math.max(dp[i - 1], dp[i - 2] + (nums[i] <= k? 1: 0));
        }
        return dp[n - 1];
    }
}

LCP 06. 拿硬币（简单贪心模拟）

https://leetcode.cn/problems/na-ying-bi/

class Solution {
    public int minCount(int[] coins) {
        int ans = 0;
        for (int x: coins) ans += (x + 1) / 2;
        return ans;
    }
}

2603. 收集树中金币⭐

https://leetcode.cn/problems/collect-coins-in-a-tree/description/?envType=daily-question&envId=2023-09-21

提示：
n == coins.length
1 <= n <= 3 * 10^4
0 <= coins[i] <= 1
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵合法的树。

难度分 2712 是因为当时美国站点崩了，很多人没看到题。

思路——拓扑排序删边

https://leetcode.cn/problems/collect-coins-in-a-tree/solutions/2191371/tuo-bu-pai-xu-ji-lu-ru-dui-shi-jian-pyth-6uli/?envType=daily-question&envId=2023-09-21

先去掉所有没有金币的叶子节点。
再去掉最外两层的节点。
最后的答案就是剩余的边数 * 2。

class Solution {
    public int collectTheCoins(int[] coins, int[][] edges) {
        int n = coins.length;
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        int[] deg = new int[n];     // 记录每个节点的入度
        for (int[] e: edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
            deg[x]++;
            deg[y]++;
        }

        int leftEdges = n - 1;      // 记录剩余的边数
        // 拓扑排序，去掉所有没有金币的子树
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < n; ++i) {
            if (deg[i] == 1 && coins[i] == 0) q.offer(i);
        }
        while (!q.isEmpty()) {
            leftEdges--;            // 删除当前节点和其父节点之间的边
            for (int y: g[q.poll()]) {
                if (--deg[y] == 1 && coins[y] == 0) {
                    q.offer(y);
                }
            }
        }

        // 再次拓扑排序，删除最外两层的节点
        for (int i = 0; i < n; ++i) {
            if (deg[i] == 1 && coins[i] == 1) q.offer(i);
        }
        leftEdges -= q.size();
        for (int x: q) {
            for (int y: g[x]) {
                if (--deg[y] == 1) leftEdges--;
            }
        }
        return Math.max(leftEdges * 2, 0);
    }
}

2591. 将钱分给最多的儿童（分类讨论）

https://leetcode.cn/problems/distribute-money-to-maximum-children/description/?envType=daily-question&envId=2023-09-22

class Solution {
    public int distMoney(int money, int children) {
        if (money < children) return -1;
        money -= children;
        int x = Math.min(money / 7, children);      // 计算最多多少个儿童分到8美元
        int y = money - x * 7;                      // 计算剩余的美元
        if ((x == children - 1 && y == 3 ) || (x == children  && y > 0)) return x - 1;
        return x;
    }
}

1993. 树上的操作（设计数据结构）

https://leetcode.cn/problems/operations-on-tree/description/?envType=daily-question&envId=2023-09-23

提示：
n == parent.length
2 <= n <= 2000
对于 i != 0 ，满足 0 <= parent[i] <= n - 1
parent[0] == -1
0 <= num <= n - 1
1 <= user <= 10^4
parent 表示一棵合法的树。
lock ，unlock 和 upgrade 的调用 总共 不超过 2000 次。

class LockingTree {
    int[] parent;
    int[] lockNodeUser;
    List<Integer>[] g;      // 存储所有儿子

    public LockingTree(int[] parent) {
        int n = parent.length;
        this.parent = parent;
        lockNodeUser = new int[n];
        Arrays.fill(lockNodeUser, -1);
        g = new List[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int i = 0; i < n; ++i) {
            if (parent[i] != -1) g[parent[i]].add(i);
        }
    }
    
    public boolean lock(int num, int user) {
        if (lockNodeUser[num] == -1) {
            lockNodeUser[num] = user;
            return true;
        }
        return false;
    }
    
    public boolean unlock(int num, int user) {
        if (lockNodeUser[num] == user) {
            lockNodeUser[num] = -1;
            return true;
        }
        return false;
    }
    
    public boolean upgrade(int num, int user) {
        // 自己没被上锁，没有祖宗上锁，有子孙节点上锁了
        boolean res = lockNodeUser[num] == -1 && !hasLockedAncestor(num) && checkAndUnlockDescendant(num);
        if (res) lockNodeUser[num] = user;
        return res;
    }

    // 是否有祖宗节点被上锁
    public boolean hasLockedAncestor(int num) {
        num = parent[num];
        while (num != -1) {
            if (lockNodeUser[num] != -1) return true;
            num = parent[num];
        }
        return false;
    }

    // 是否有子孙节点被上锁，并解锁
    public boolean checkAndUnlockDescendant(int num) {
        boolean res = lockNodeUser[num] != -1;
        lockNodeUser[num] = -1;         
        for (int y: g[num]) {
            res |= checkAndUnlockDescendant(y);
        }
        return res;
    }
}

/**
 * Your LockingTree object will be instantiated and called as such:
 * LockingTree obj = new LockingTree(parent);
 * boolean param_1 = obj.lock(num,user);
 * boolean param_2 = obj.unlock(num,user);
 * boolean param_3 = obj.upgrade(num,user);
 */

这题的重点在于操作三的实现。

146. LRU 缓存（⭐数据结构：哈希表+双向链表）

https://leetcode.cn/problems/lru-cache/description/?envType=daily-question&envId=2023-09-24

提示：

1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 10^5
最多调用 2 * 10^5 次 get 和 put

解法1——哈希表+双向链表⭐

双向链表维护各个节点被使用的情况，头节点是最近被使用的，尾节点是最久未被使用的。
哈希表维护key和节点之间的映射，帮助快速找到指定key的节点。

class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {};
        public DLinkedNode(int _key, int _value) {
            this.key = _key;
            this.value = _value;
        }
    }

    Map<Integer, DLinkedNode> cache = new HashMap<>();  // key和节点的映射
    int size = 0;       // 大小
    int capacity;       // 容量
    // 虚拟头尾节点
    DLinkedNode head = new DLinkedNode(), tail = new DLinkedNode();

    public LRUCache(int capacity) {
        this.capacity = capacity;
        head.next = tail;
        tail.prev = head;
    }
    
    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) return -1;
        moveToHead(node);
        return node.value;
    }
    
    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            DLinkedNode newNode = new DLinkedNode(key, value);
            cache.put(key, newNode);
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                DLinkedNode last = removeTail();    
                cache.remove(last.key);
                --size;
            } 
        } else {
            node.value = value;
            moveToHead(node);
        }
    }

    // 将节点添加到头部
    public void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    // 删除节点
    public void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    // 将节点移动到头部
    public void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    // 删除最后一个节点
    public DLinkedNode removeTail() {
        DLinkedNode node = tail.prev;
        removeNode(node);
        return node;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

解法2——Java JDK LinkedHashMap

class LRUCache extends LinkedHashMap<Integer, Integer>{
    private int capacity;

    public LRUCache(int capacity) {
        super(capacity, 0.75F, true);
        this.capacity = capacity;
    }
    
    public int get(int key) {
        return super.getOrDefault(key, -1);
    }
    
    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity;
    } 
}

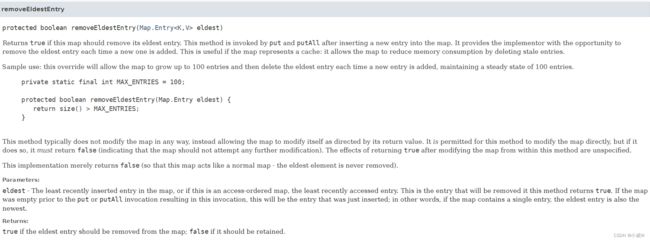
补充——LinkedHashMap

https://docs.oracle.com/en/java/javase/11/docs/api/java.base/java/util/LinkedHashMap.html

构造器：

---

protected boolean removeEldestEntry​(Map.Entry eldest)
如果此映射应该删除其最年长的条目，则返回true。在向映射中插入新条目后，put和putAll调用该方法。它为实现者提供了每次添加新条目时删除最老条目的机会。如果映射表示缓存，这很有用:它允许映射通过删除过时的条目来减少内存消耗。

补充——Java修饰符