【多目标进化优化】多目标进化算法的收敛性
声明
本文内容来源于 《多目标进化优化》 郑金华 邹娟著,非常感谢两位老师的知识分享,如有侵权,本利立即删除,同时在此表示,本文内容仅学习使用,也禁止他人侵权,谢谢!
0 前言
\quad\quad 对 M O E A MOEA MOEA 收敛性的研究是 M O E A MOEA MOEA 研究的重要内容,但目前这方面的研究结果比较少。 一个 M O E A MOEA MOEA 的收敛性可以从两个方面考虑;一是有限时间内的收敛;二是当时间趋向于无穷大时的收敛。第一类收敛是最理想的,也是 M O E A MOEA MOEA 设计所追求的,但这方面的研究结果很少。第二类收敛是理论上的收敛,它对 M O E A MOEA MOEA 设计也具有指导意义。目前的多数工作主要集中于对第二类收敛的研究。本文通过建立 M O E A MOEA MOEA 的简单进化模型来讨论有限时间内的收敛;同时讨论一般情况下 M O E A MOEA MOEA 在理论上的收敛性。
1. 多目标进化模型及其收敛性分析
\quad\quad 本节我们先讨论 M O E A MOEA MOEA 的简单进化模型,并定义一些 r e d u c e reduce reduce 函数,然后论证其收敛性。
1.1 多目标进化简单模型
\quad\quad 定义 5.1(目标空间) \quad 设有限集 Z Z Z 是目标空间中所有可行解的集合,即 Z ∈ P r , r ≥ 2 Z \in P^r,r≥2 Z∈Pr,r≥2 为目标数。(多目标优化中将原始的 x x x 组成的集合叫决策空间,此处定义目标空间用 Z Z Z 来表示)
\quad\quad 定义 5.2(Pareto 最优边界) \quad 设有限集 Z ∗ Z^* Z∗ 表示 Z Z Z 的 P a r e t o Pareto Pareto 最优边界集合, Z ∗ = { z ∗ ∈ Z ∣ ∄ z ∈ Z , z ≻ z ∗ } Z^* = \{z^* \in Z|\not \exists z \in Z, z \succ z^*\} Z∗={z∗∈Z∣∃z∈Z,z≻z∗}
\quad\quad 定义 5.3(归档集) 设有限集 M t ⊆ Z M_t \subseteq Z Mt⊆Z 为时间 t t t (或第 t t t 代)的归档集。(即在第 t 代所产生的最优非支配解集)
\quad\quad 定义 5.4(个体产生过程) 过程 G e n ( t ) Gen(t) Gen(t) 在时间 t t t 产生的个体为 z t ∈ Z z_t \in Z zt∈Z。对 Z Z Z 中每个个体 z z z ,在时间 t t t 通过 G e n ( t ) Gen(t) Gen(t) 产生 z z z 的概率为 p r ( t , z ) , p r ( t , z ) > 0 p_r(t, z), p_r(t, z)>0 pr(t,z),pr(t,z)>0 \quad ( G e n ( t ) Gen(t) Gen(t):表示某一种进化算法)
\quad\quad 定义 5.5(非支配集过滤器) 任给一个目标向量集 Z 1 Z^1 Z1,它的非支配集为 N D S e t ( Z 1 ) NDSet(Z^1) NDSet(Z1): (即用 N D S e t ( Z 1 ) NDSet(Z^1) NDSet(Z1) 来表示 Z 1 Z^1 Z1 的非支配集)
N D S e t ( Z 1 ) = { z i ∈ Z 1 ∣ ∄ z j ∈ Z 1 , z j ≻ z i , i , j ∈ 1 ⋅ ⋅ ⋅ ∣ Z 1 ∣ } NDSet(Z^1) = \{z^i \in Z^1 |\not \exists z^j \in Z^1, z^j \succ z^i, i, j \in 1 ··· |Z^1| \} NDSet(Z1)={zi∈Z1∣∃zj∈Z1,zj≻zi,i,j∈1⋅⋅⋅∣Z1∣}
\quad\quad 定义 5.6 \quad 设向量 z a z^a za, 非支配集 Z n d = N D S e t ( Z n d ) , z a Z_{nd} = NDSet(Z_{nd}),z^a Znd=NDSet(Znd),za 和 Z n d Z_{nd} Znd 之间的关系定义如下: ( z a z^a za:表示 a 这个个体,为向量是因为含有多个目标,且每个目标可能含有多个变量)
\quad\quad ① z a ≻ Z n d ⇔ ∃ z ∈ Z n d , 有 z a ≻ z z^a \succ Z_{nd} \Leftrightarrow \exists z \in Z_{nd}, 有 z^a \succ z za≻Znd⇔∃z∈Znd,有za≻z
\quad\quad ② Z n d ≻ z a ⇔ ∃ z ∈ Z n d , 有 z ≻ z a ,或者 Z n d ≻ z a ⇔ Z n d = N D S e t ( { z a } ∪ Z n d ) , 且 z ∉ Z n d Z_{nd} \succ z^a \Leftrightarrow \exists z \in Z_{nd}, 有 z \succ z^a,或者 Z_{nd} \succ z^a \Leftrightarrow Z_{nd} =NDSet(\{z^a\} \cup Z_{nd}), 且 z \not \in Z_{nd} Znd≻za⇔∃z∈Znd,有z≻za,或者Znd≻za⇔Znd=NDSet({za}∪Znd),且z∈Znd
\quad\quad ③ z a ∽ Z n d ⇔ z a ⊁ Z n d ∧ Z n d ⊁ z a ,且 z ∉ Z n d z^a \backsim Z_{nd} \Leftrightarrow z^a \not \succ Z_{nd} \wedge Z_{nd} \not \succ z^a,且 z \not \in Z_{nd} za∽Znd⇔za≻Znd∧Znd≻za,且z∈Znd 。( 即表示: z a z^a za 与 Z n d Z_{nd} Znd 无关,互不支配)
\quad\quad 在讨论 M O E A MOEA MOEA 的收敛性之前,为简便起见,先建立一个简化了的 M O E A MOEA MOEA 模型,如算法 5.1 (simple MOEA, SMOEA)所示。虽然 S M O E A SMOEA SMOEA 在每一代进化时只产生一个新个体,但很容易将 S M O E A SMOEA SMOEA 扩展为一般的 M O E A MOEA MOEA,即在每一代进化时产生多个新个体。

\quad\quad 定义 5.7(收敛) 当 M t M_t Mt 中所有个体在进一步运行 S M O E A SMOEA SMOEA 时不再发生变化,即 ∀ t > t c \forall t > t_c ∀t>tc,有 M t = M t c M_t = M_{t_{c}} Mt=Mtc,则称 M t M_t Mt 收敛。 (即随着新一代产生,归档集中的个体不发生变化时,收敛)
1.2 reduce 函数
(1)unbounded reduce 函数
\quad\quad unbounded reduce 函数非常简单,每次产生一个新个体时,只有当它对归档集是非支配的,才将该个体加人到归档集,并将归档集中被它所支配的所有个体删除,如算法 5.2 所示。容易证明,unbounded reduce 函数可以使 SMOEA 收敛到最优解集。由此,归档集的大小取决于可行解集 Z Z Z 的大小,而 Z Z Z 可能很大,因此这类算法的实用价值不大。

(2)simple bounded reduce 函数
\quad\quad simple bounded reduce 函数与 unbounded reduce函数的不同之处在于,归档集的大小为一约定值 arcsize。这样,当新个体支配归档集时,将它加入到归档集中,同时删除归档集中被该个体所支配的个体;否则,只有当归档集不满时,即当 ( ∣ M t − 1 − 1 ∣ | M_{t-1}-1 | ∣Mt−1−1∣ < arcsize)时,才将它加入到归档集中,同时删除归档集中被该个体所支配的个体。如算法 5.3 所示。容易证明 simple bounded reduce 函数可以使 SMOEA 收敛到最优解集的一个子集,但解集具有比较差的分布性。

(3)S-metric reduce 函数
- S ( A ) S(A) S(A) :由一组目标向量所支配的区域
\quad\quad 在 S-metric reduce 函数中,当有新的非支配个体产生时,利用 S-metric 来保持归档集中个体的分布性。S-metric 最早由 Zitzler 等提出(Zitzler et al,1999a), Fleischer 也对它 (Fleischer, 2003)进行了比较详细的讨论。S-metric 类似于 hypervolume measure 方法,是目标空间中被非支配集所支配的一块区域,如图 5.1 所示。在图 5.1 的左上部,三个向量 { z 1 , z 2 , z 3 } \{z^1,z^2,z^3\} {z1,z2,z3} 共同支配的区域为 S(A),在图 5.1 的右上部,三个向量 { z 1 , z 2 , z 3 } \{z^1,z^2,z^3\} {z1,z2,z3} 共同支配的区域为 S(B),有 S(A) > S(B)。在图 5.1 的下半部分,由于参考向量 z r e f z^{ref} zref 在第二个目标上的值变大,而在第一个目标上的值又变小了,这样,三个向量 { z 1 , z 2 , z 3 } \{z^1,z^2,z^3\} {z1,z2,z3} 共同支配的区域发生了变化,此时有 S(A) < S(B)。由此可见,S-metric 与参考向量的选取有关。 ( z r e f z^{ref} zref:参考向量)

\quad\quad 给定向量集 A = { z 1 , z 2 , … } A = \{z^1 , z^2 ,…\} A={z1,z2,…},其中 z i = { z 1 i , z 2 i , … , z r i } z^i=\{z_1^i, z_2^i ,…, z_r^i\} zi={z1i,z2i,…,zri} 和一个参考向量 z r e f = { z 1 r e f , z 2 r e f , . . . , z r r e f } z^{ref} = \{z_1^{ref}, z_2^{ref}, ..., z_r^{ref}\} zref={z1ref,z2ref,...,zrref}, 定义 R ( A , z r e f ) R(A, z^{ref}) R(A,zref) 为:
R ( A , z r e f ) = ∪ i ∈ 1... ∣ A ∣ R ( z i , z r e f ) R(A, z^{ref}) = \cup_{i \in 1...|A|} R(z^i, z^{ref}) R(A,zref)=∪i∈1...∣A∣R(zi,zref)
式中, R ( z i , z r e f ) = { y ∣ y ≻ z r e f ∧ z i ≻ y , y ∈ R r } R(z^i, z^{ref}) = \{y|y \succ z^{ref} \wedge z^i \succ y, y \in \Bbb{R}^r\} R(zi,zref)={y∣y≻zref∧zi≻y,y∈Rr} (即向量集 A 中的每个向量与参考向量之间的区域,如图 5.1 中的 S 区域)
\quad\quad A A A 的 S − m e t r i c S-metric S−metric 是 A A A 与参考向量 z r e f z^{ref} zref 之间的一块区域,或者说是 R ( z i , z r e f ) R(z^i, z^{ref}) R(zi,zref) 的 Lebesgue integral 积分
\quad\quad 在只有 2 个目标的情况下, S ( A ) S(A) S(A) 的计算可表示为
S ( A ) = ∑ i ∈ 1... ∣ A ∣ ∣ z 1 i − z 1 r e f ∣ ⋅ ∣ z 2 i − z 2 i − 1 ∣ S(A) = \sum_{i \in 1...|A|} |z_1^i - z_1^{ref} | \cdot |z_2^i - z_2^{i-1}| S(A)=i∈1...∣A∣∑∣z1i−z1ref∣⋅∣z2i−z2i−1∣
式中, z 2 0 = z 2 r e f z_2^0 = z_2^{ref} z20=z2ref。(其中 z 1 i z^i_1 z1i 表示第 i i i 个个体的第 1 个目标向量,即上标表示个体,下标表示目标)
\quad\quad 当目标数大于 2 时,计算 S ( A ) S(A) S(A) 比较复杂一些,这里介绍一个用递归计算 S ( A ) S(A) S(A) 的方法 s i z e − o f − s e t ( A , z r e f , r ) size-of-set(A, z^{ref}, r) size−of−set(A,zref,r),如算法 5.4 所示。值得说明的是,在计算 S ( A ) S(A) S(A) 时,要在第一个目标上对 A A A 中个体按降序排序。


1.3 收敛性分析
\quad\quad 下面来讨论 S − m e t r i c r e d u c e S-metric reduce S−metricreduce 函数的收敛性,即讨论 S − m e t r i c r e d u c e S-metric reduce S−metricreduce 函数是否可以使 S M O E A SMOEA SMOEA 收敛到最优解集。为了讨论方便,这里将 S M O E A + S − m e t r i c r e d u c e SMOEA + S-metric reduce SMOEA+S−metricreduce 函数表示为 S M O E A S SMOEAS SMOEAS
\quad\quad 引理 5.1 \quad 若 M t − 1 M_{t-1} Mt−1 是一个非支配集,在时刻 t t t 应用了 ( r u l e : s i z e ) (rule: size) (rule:size),则 M t M_t Mt 仍为非支配集。也就是说, ( r u l e : s i z e ) (rule: size) (rule:size) 能维持归档集为一个非支配集。 ( ( r u l e : s i z e ) (rule: size) (rule:size):表示通过进化算法产生新的个体 z t z_t zt,并利用 S-metric reduce 函数筛选后得到了 M t M_t Mt)

\quad\quad 引理 5.2 \quad 若存在 t , t, t, S M O E A − S SMOEA-S SMOEA−S 使 M t M_t Mt 收敛,则有 M t ⊆ Z ∗ M_t \subseteq Z^* Mt⊆Z∗ \quad ( Z ∗ Z^* Z∗ 为 Pareto 最优边界组成的集合,都收敛了肯定属于 Z ∗ Z^* Z∗)

\quad\quad 引理 5.3 \quad 若 t n > t m , M t n ≠ M t m t_n > t_m,M_{t_n} ≠ M_{t_m} tn>tm,Mtn=Mtm,则 ∀ t > t m , M t ≠ M t m \forall t > t_m, M_{t} ≠ M_{t_m} ∀t>tm,Mt=Mtm

\quad\quad 引理 5.4 \quad 存在 t , S M O E A − S t,SMOEA-S t,SMOEA−S 使 M t M_t Mt 收敛。

\quad\quad 引理 5.5 \quad S M O E A − S SMOEA-S SMOEA−S 使 M t M_t Mt 收敛到 Z ∗ Z^* Z∗ 的子集。

2. 自适应网格算法及其收敛性
\quad\quad 在 多目标进化群体的分布性 一文中已经讨论了自适应网格技术,这里将具体讨论自适应网格算法(adaptive grid algorithm, AGA),并对其收敛性进行分析。由于采用 A G A AGA AGA 保持进化群体分布性时,不能有效地阻止某些非支配个体多次循环地进入和移出归档集,因此 S M O E A + A G A ( 简称 S M O E A − A ) SMOEA+AGA (简称SMOEA-A) SMOEA+AGA(简称SMOEA−A) 不能满足定义 5.7 的收敛性, 但 S M O E A − A SMOEA-A SMOEA−A 能使进化群体具有良好的分布性。
2.1 有关定义
为了讨论方便,先给出有关定义
\quad\quad 定义 5.8 \quad 设第 t − 1 t-1 t−1 代归档集为 M t − 1 , G e n ( t ) M_{t-1},Gen(t) Mt−1,Gen(t) 产生的新个体为 z t z_t zt ,则 N t = N D S e t ( { z t } ∪ M t − 1 ) N_t = NDSet(\{z_t\} \cup M_{t-1}) Nt=NDSet({zt}∪Mt−1)。注意,此时可能有 ∣ N t ∣ > a r c s i z e |N_t| > arcsize ∣Nt∣>arcsize。 ( N t N_t Nt:表示第 t 代的非支配集)
\quad\quad 定义 5.9 \quad 可行解集 Z Z Z 中,设第 k k k 个目标的最大和最小值分别表示为 m a x z k , z maxz_{k, z} maxzk,z 和 m i n z k , z minz_{k, z} minzk,z ,其中 m a x z k , z = m a x z ∈ Z ( z k ) , m i n z k , z = m i n z ∈ Z ( z k ) maxz_{k, z} = max_{z \in Z}(z_k), minz_{k, z} = min_{z \in Z}(z_k) maxzk,z=maxz∈Z(zk),minzk,z=minz∈Z(zk) 。 则 N t N_t Nt 中,第 k k k 个目标的域宽 r a n g e k , t = m a x { z k ∣ z ∈ N t } − m i n { z k ∣ z ∈ N t } range_{k,t} = max\{z_k | z \in N_t\} - min\{z_k | z \in N_t\} rangek,t=max{zk∣z∈Nt}−min{zk∣z∈Nt} \quad (第 k 个目标的域宽即为非支配集中,最大向量 - 最小向量)
\quad\quad 定义 5.10 \quad 一个自适应网格,需要设置 2 r 2r 2r 个边界:下界 ( l b k ) (lb_k) (lbk) 和上界 ( u b k ) ( k = 1 , 2 , . . . , r ) , r (ub_k) (k = 1, 2, ..., r), r (ubk)(k=1,2,...,r),r 为目标数。 ∀ t , ∀ k , l b k , t < m i n { z k ∣ z ∈ N t } \forall t, \forall k, lb_{k, t} < min\{z_k | z \in N_t\} ∀t,∀k,lbk,t<min{zk∣z∈Nt} 且 u b k , t > m a x { z k ∣ z ∈ N t } ub_{k, t} > max\{z_k | z \in N_t\} ubk,t>max{zk∣z∈Nt}。 (第 k 个目标的下界小于非支配集中的最小向量,上界大于最大向量)
\quad\quad 定义 5.11 \quad 用超立方体的两个对角标识一个自适应网格: ( l b 1 , t , l b 2 , t , . . . . , l b r , t ) (lb_{1,t}, lb_{2,t}, ...., lb_{r,t}) (lb1,t,lb2,t,....,lbr,t) 和 ( u b 1 , t , u b 2 , t , . . . . , u b r , t ) , (ub_{1,t}, ub_{2,t}, ...., ub_{r,t}), (ub1,t,ub2,t,....,ubr,t), 它可以被分割为若干个小网格(或区域) r t i ∈ R t r_t^i \in R_t rti∈Rt 这里 i = ( i 1 , i 2 , . . . , i r ) i = (i_1, i_2, ..., i_r) i=(i1,i2,...,ir),且有 i k ∈ { 1 , 2 , . . . , d } , d ∈ Z i_k \in \{1, 2, ..., d\}, d \in \Bbb Z ik∈{1,2,...,d},d∈Z 是一个常数,表是在每一维上的分割次数,一般为大于 2 的自然数。具体的分割次数取决于进化群体的大小和待优化问题的目标数。将所有小网格 r t i ∈ R t r_t^i \in R_t rti∈Rt 的坐标 i i i 表示为 I I I 的集合,有 ∣ I ∣ = d r |I| = d^r ∣I∣=dr。 \quad (对于这里 r t i r_t^i rti 不怎么清楚的朋友,可以先看一下我另一篇博文的网格部分:多目标进化群体的分布性)
\quad\quad 定义 5.12 \quad 每个小网格 r t i ∈ R t r_t^i \in R_t rti∈Rt 的边界定义如下:
∀ k ∈ { 1 , 2 , . . . , r } , r u b k , i , t = l b k , t + i k × w k , t \forall k \in \{1, 2, ..., r\}, rub_{k, i, t} = lb_{k, t} + i_k × w_{k, t} ∀k∈{1,2,...,r},rubk,i,t=lbk,t+ik×wk,t
r l b k , i , t = l b k , t + ( i k − 1 ) × w k , t rlb_{k, i, t} = lb_{k, t} + (i_k - 1)× w_{k, t} rlbk,i,t=lbk,t+(ik−1)×wk,t
其中 w k , t w_{k, t} wk,t 为每一个小网格在第 k k k 维上的宽度 , w k = r a n g e k , t / d , , r a n g e k , t , w_k = range_{k, t}/d,,range_{k, t} ,wk=rangek,t/d,,rangek,t 为第 k k k 维上的域宽。 ( r t i r_t^i rti 即如下的很多个小网格区域)
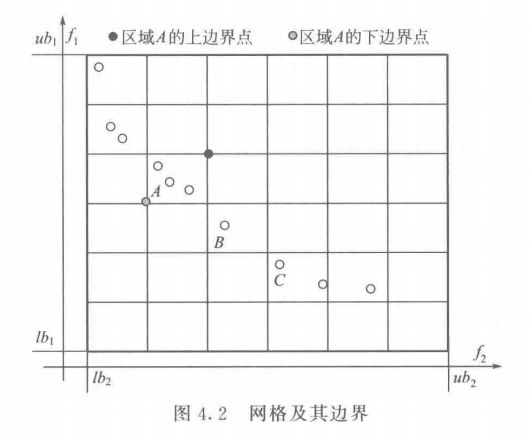
\quad\quad 定义 5.13 (占用区) \quad 设 z ∈ M t − 1 , z \in M_{t-1} , z∈Mt−1, 对区域 r t i , r_t^i, rti, 若 ∀ k ∈ { 1 , 2 , . . . , r } , z k ≥ r l b k , i , t \forall k \in \{1, 2, ..., r\}, z_k ≥ rlb_{k, i, t} ∀k∈{1,2,...,r},zk≥rlbk,i,t 且 z k < r u b k , i , t , z_k < rub_{k, i, t}, zk<rubk,i,t, 则称个体 z z z 在区域 r t i r_t^i rti 中,并将 r t i r_t^i rti 称为占用区(occupied region,OR)
\quad\quad 定义 5.14 (Pareto 占用区) \quad 设 z ∈ Z ∗ z \in Z^* z∈Z∗ ( z z z 可以不在 M t − 1 M_{t-1} Mt−1 中),对区域 r t i r_t^i rti,若 ∀ k ∈ { 1 , 2 , . . . , r } , z k ≥ r l b k , i , t \forall k \in \{1, 2, ..., r\}, z_k ≥ rlb_{k, i, t} ∀k∈{1,2,...,r},zk≥rlbk,i,t 且 z k < r u b k , i , t z_k < rub_{k, i, t} zk<rubk,i,t ,则将 r t i r_t^i rti 称为 Pareto 占用区(Pareto occupied region, POR)。
\quad\quad 定义 5.15 \quad p ( r t i ) p(r_t^i) p(rti) 为区域 r t i r_t^i rti 中所有个体的计数,即 p ( r t i ) = ∣ { z ∈ M t − 1 ∣ ∀ k ∈ { 1 , 2 , . . . , r } , z k ≥ r l b k , i , t ∧ z k < r u b k , i , r } ∣ p(r_t^i) = | \{z \in M_{t-1} | \forall k \in \{1, 2, ..., r\}, z_k ≥ rlb_{k, i, t} \wedge z_k < rub_{k, i, r}\} | p(rti)=∣{z∈Mt−1∣∀k∈{1,2,...,r},zk≥rlbk,i,t∧zk<rubk,i,r}∣。 \quad (注意这里是对 M t − 1 M_{t-1} Mt−1 中的个体进行计数)
\quad\quad 定义 5.16 \quad o c c ( r t i , Z ) occ(r_t^i, Z) occ(rti,Z) 为区域 r t i r_t^i rti 中所有个体的集合,即 o c c ( r t i , Z ) = { z ∈ Z ∣ ∀ k ∈ { 1 , 2 , . . . , r } , z k ≥ r l b k , i , t ∧ z k < r u b k , i , r } , o c c ( r t i , Z ) ⊆ Z occ(r_t^i, Z) = \{z \in Z | \forall k \in \{1, 2, ..., r\},z_k ≥ rlb_{k, i, t} \wedge z_k < rub_{k, i, r} \}, occ(r_t^i, Z) \subseteq Z occ(rti,Z)={z∈Z∣∀k∈{1,2,...,r},zk≥rlbk,i,t∧zk<rubk,i,r},occ(rti,Z)⊆Z
\quad\quad 定义 5.17 \quad 在时间 t , t, t, 被向量 z z z 所占用的区域 r t i r_t^i rti,表示为 r t i ( z ) r_t^{i(z)} rti(z)
\quad\quad 定义 5.18 \quad 在 N t N_t Nt 中的极点向量(uniquely extremal vectors)定义为: \quad ( N t N_t Nt:第 t 代的非支配集)
z e x t = { y ∈ N t ∣ ( ∃ k ∈ { 1 , 2 , . . . , r } , ∄ z ∈ N t , z ≠ y , z k ≤ y k ) ∨ ( ∃ k ∈ { 1 , 2 , . . . , r } , ∄ z ∈ N t , z ≠ y , z k ≥ y k ) } z^{ext} = \{y \in N_t | (\exists k \in \{1, 2, ..., r\}, \not \exists z \in N_t, z ≠ y, z_k ≤ y_k) \vee (\exists k \in \{1, 2, ..., r\}, \not \exists z \in N_t, z ≠ y, z_k ≥ y_k)\} zext={y∈Nt∣(∃k∈{1,2,...,r},∃z∈Nt,z=y,zk≤yk)∨(∃k∈{1,2,...,r},∃z∈Nt,z=y,zk≥yk)}
\quad\quad 也就是说,在某个目标上其值最大或最小的个体均被认为是极点。极点总是分布在端点位置上,它有利于使进化群体具有更好的分布性,故而在执行选择操作时,一般不能让极点丢失。
\quad\quad 定义 5.19 \quad 在区域 r t i r_t^i rti 中,将除去极点后所有个体的集合(non-uniquely extremal vectors)定义为 n u e ( r t i ) , nue(r_t^i), nue(rti), 即 n u e ( r t i ) = o c c ( r t i , Z ) \ z e x t nue(r_t^i) = occ(r_t^i, Z) \backslash z^{ext} nue(rti)=occ(rti,Z)\zext。 ( \ \backslash \ 并不是除法,表示除去其中的向量)
\quad\quad 定义 5.20(最大区域聚集) \quad 定义 p u n e ( r t i ) = ∣ n u e ( r t i ) ∣ , p_{une}(r_t^i) = |nue(r_t^i)| , pune(rti)=∣nue(rti)∣, 则当 p u n e ( r t i ) p_{une}(r_t^i) pune(rti) 具有最大值时,表明在区域 r t i r_t^i rti 聚集的个体最多(crowded region, CR),将所有 C R CR CR 的集合定义为 C R t = { i ∈ I ∣ m a x ( p u n e ( r t i ) ) } CR_t = \{i \in I | \ max(p_{une}(r_t^i))\} CRt={i∈I∣ max(pune(rti))}
\quad\quad 定义 5.21 \quad 定义时间 t , t, t, 所有 C R CR CR 中的个体组成的集合为 Z c , t = { z ∣ z ∈ ∪ n u e ( r t i ) , r t i ∈ C R t } Z_{c,t} = \{z | z \in \cup nue(r_t^i), r_t^i \in CR_t\} Zc,t={z∣z∈∪nue(rti),rti∈CRt} \quad (最大区域聚集中的个体)
\quad\quad 在 Z c , t Z_{c,t} Zc,t 中,其个体的聚集程度最大,因此,为保持进化群体的分布性,通常从 Z c , t Z_{c,t} Zc,t 中随机选取个体 z c , t ∈ Z c , t z_{c,t} \in Z_{c,t} zc,t∈Zc,t 删除
\quad\quad 值得说明的是,在以上定义中,假定 ∀ t , k ∈ { 1 , 2 , . . . , r } , m a x { z k ∣ z ∈ N t } ≠ m i n { z k ∣ z ∈ N t } \forall t, k \in \{1,2,... ,r \}, max\{z_k | z \in N_t\} ≠ min\{z_k | z \in N_t\} ∀t,k∈{1,2,...,r},max{zk∣z∈Nt}=min{zk∣z∈Nt} , 同时假设归档集大小 a r c s i z e > 2 r , arcsize>2r, arcsize>2r,这里 r r r 为目标数。
2.2 自适应网格算法


2.3 AGA 收敛性分析
\quad\quad 要分析 AGA(自适应网格算法) 的收敛性,就必须考虑网格的边界,网格中的每一个区域的边界,以及进化个体在这些区域中的分布等,本节讨论 AGA 在一定条件下是收敛的。
\quad\quad 引理 5.5 \quad 设在时间 t t t 产生的向量为 z t ∈ Z z_t \in Z zt∈Z, 如果对一些 j ∈ { 1 , 2 , . . . , r } j \in \{1, 2, ..., r\} j∈{1,2,...,r},有 z j = m i n z j , Z z_j = minz_{j, Z} zj=minzj,Z,则 m i n z j , M t = m i n z j , Z minz_{j, M_t} = minz_{j, Z} minzj,Mt=minzj,Z

\quad\quad 引理 5.6 \quad 如果对一些 j ∈ { 1 , 2 , . . . , r } , ∃ z ∈ M t m 使 z j = m i n z j , Z , j \in \{1, 2, ..., r\}, \exists z \in M_{t_m} 使 z_j = minz_{j, Z}, j∈{1,2,...,r},∃z∈Mtm使zj=minzj,Z, 则 ∀ t > t m , ∃ z ∈ M t \forall t > t_m,\exists z \in M_t ∀t>tm,∃z∈Mt 使 z j = m i n z j , Z z_j = minz_{j, Z} zj=minzj,Z

\quad\quad 定理 5.2 \quad 网格的下边界 ( l b k , t lb_{k,t} lbk,t) 收敛, k ∈ { 1 , 2 , . . . , r } k \in \{1, 2, ..., r\} k∈{1,2,...,r}

\quad\quad 定理 5.2 表明了上边界是收敛的。但对于上边界,它在一般条件下是不收敛的,只有在某种特定的条件下才收敛。为了后续讨论,先假定上边界也是收敛的。
\quad\quad 假设 5.1 \quad 网格的上边界 ( u b k , t ub_{k, t} ubk,t) 收敛, k ∈ { 1 , 2 , . . . , r } k \in \{1, 2, ..., r\} k∈{1,2,...,r}
\quad\quad 推论 5.1 \quad 网格中所有小网格(区域)的边界是收敛。
\quad\quad 推论 5.1 是由定理 5.2 和假设 5.1 得出的。接下来的讨论将依赖于推论 5.1。为便于进 一步的讨论,下面先定义有关术语。
\quad\quad 定义 5.22 \quad 将边界收敛的区域的集合定义为区域收敛集,每个这样的区域定义为收敛区域(converged region, CR)。
\quad\quad 定义 5.23 \quad 若一个区域收敛集的子集总是被占用,则说存在占用区域的收敛集(a converged set of occupied regions),表示为 R C O R R_{COR} RCOR,并将这样的区域称为常占区(constantly occupied region, COR) 。
\quad\quad 定义 5.24 \quad 我们说一个区域厂 r ( 1 ) r^{(1)} r(1) 优于另一个区域 r ( 2 ) r^{(2)} r(2),或者说 r ( 2 ) r^{(2)} r(2) 比 r ( 1 ) r^{(1)} r(1) 劣,当且仅当 r ( 1 ) r^{(1)} r(1) 的坐标均小于 r ( 2 ) r^{(2)} r(2) 的。
\quad\quad 这样,在 r ( 2 ) r^{(2)} r(2) 中的个体均被 r ( 1 ) r^{(1)} r(1) 中的个体所支配,任何一个比 P O R POR POR 差的区域不可能是 P O R , POR, POR, 如图 5. 2 所示 (POR:Pareto 占用区)

\quad\quad 定义 5.25 \quad 当 r ( 1 ) r^{(1)} r(1) 的坐标小于等于 r ( 2 ) r^{(2)} r(2) 的坐标时,我们说区域 r ( 1 ) r^{(1)} r(1) 稍优于区域 r ( 2 ) r^{(2)} r(2),或者说 r ( 2 ) r^{(2)} r(2) 比 r ( 1 ) r^{(1)} r(1) 稍劣。
\quad\quad 如果 r ( 2 ) r^{(2)} r(2) 比 r ( 1 ) r^{(1)} r(1) 稍劣,则在 r ( 2 ) r^{(2)} r(2) 中可能存在非支配个体,这样, r ( 2 ) r^{(2)} r(2) 可能是 POR。
\quad\quad 定义 5.26 \quad 如果两个区域之间相互没有谁优或稍优,则称这两个区域是相互不可比较的(incomparable),或称相容。
\quad\quad 定义 5.27 \quad 在收敛区域集中,不比其他任何 P O R POR POR 稍劣的 P O R POR POR 称为关键 P O R POR POR 或 C P O R ( c r i t i c a l P O R ) CPOR (critical POR) CPOR(criticalPOR) 所有 C P O R CPOR CPOR 的集合表示为 R C P O R R_{CPOR} RCPOR,如图 5.3 所示

\quad\quad 在图 5.3 中, z 1 z^1 z1 所在区域 r 2 , 2 r^{2,2} r2,2 稍优于 z 2 z^2 z2 所在区域 r 2 , 3 , r^{2,3}, r2,3, 或者 r 2 , 3 r^{2,3} r2,3 稍劣于 r 2 , 2 r^{2,2} r2,2。 r 2 , 3 r^{2,3} r2,3 中个体可能被 r 2 , 2 r^{2,2} r2,2 中个体所支配,但 r 2 , 2 r^{2,2} r2,2 中个体绝不可能被 r 2 , 3 r^{2,3} r2,3 中个体所支配。事实上, r 2 , 2 r^{2,2} r2,2 不比其他任何区域稍劣,因此它是 C P O R , CPOR, CPOR, 可见,在 C P O R CPOR CPOR 中的个体不被可行解集 Z Z Z 中任何其他个体所支配。
\quad\quad 定义 5.28 \quad 我们将 P O R POR POR 和比 P O R POR POR 稍劣的区域统称为 P a r e t o Pareto Pareto 非劣区域,或 PNIR (Pareto non-inferior region),如图 5.4 所示。在图 5.4 中, r 1 , 5 r^{1, 5} r1,5 是 P O R , POR, POR, r 2 , 5 r^{2, 5} r2,5 比 r 1 , 5 r^{1, 5} r1,5 稍劣,它们都是 PINR。
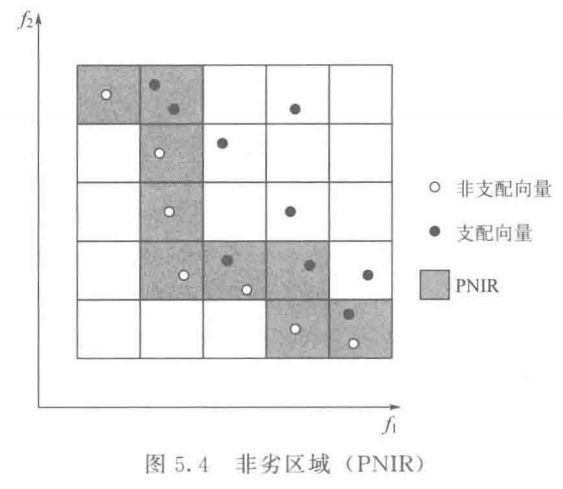
\quad\quad 引理 5.7 \quad 如果一个 C P O R CPOR CPOR 在时间 t i t_i ti 是被占用的,则对该 C P O R CPOR CPOR 也是被占用的

\quad\quad 定理 5.3 \quad 在一个有 r r r 个目标的向量空间中,非劣区域的最大数目为 d r − ( d − 1 ) r , d^r - (d-1)^r, dr−(d−1)r, 其中 d d d 为每一维空间的均分次数。
\quad\quad 引理 5.8 \quad ∀ t , G e n ( t ) \forall t, Gen(t) ∀t,Gen(t) 产生的向量为 z t ∈ Z ∗ , z_t \in Z^*, zt∈Z∗, 若 a r c s i z e > d r − ( d − 1 ) r + 2 r , arcsize > d^r - (d-1)^r + 2r, arcsize>dr−(d−1)r+2r, 则有 p ( r t i ( z t ) ) ≥ 1 p(r_t^{i(z_t)}) ≥ 1 p(rti(zt))≥1

\quad\quad 定理 5.4 \quad 若 a r c s i z e > d r − ( d − 1 ) r + 2 r , arcsize > d^r - (d-1)^r + 2r, arcsize>dr−(d−1)r+2r, 则 ∃ t m , \exists t_m, ∃tm, 使得 ∀ t > t m , ∀ r t i ∈ R C P O R , \forall t > t_m, \forall r_t^i \in R_{CPOR}, ∀t>tm,∀rti∈RCPOR, 有 p ( r t − 1 i ) > 0 p(r_{t-1}^i) > 0 p(rt−1i)>0

\quad\quad 定理 5.5 \quad 若在时间 t m t_m tm,所有的 C P O R CPOR CPOR 收敛到 R C P O R R_{CPOR} RCPOR,则 ∀ t > t m , M t \forall t > t_m , M_t ∀t>tm,Mt 中所有的个体将会占用 PNIR。



2.4 AGA 的收敛条件
\quad\quad 上一小节讨论了在网格的上边界是收敛的情况下,AGA 是收敛的。本节将讨论网格的上边界在什么条件下收敛。
\quad\quad 一种特殊情况是,当目标数为 2,同时在每个目标上最优边界的宽度与整个搜索空间的宽度相同,这种情况下网格的上边界是收敛的。然而,对于一般情况,结果未必正确,如个体循环地进入归档集和从归档集中移出,这种情况的上边界是不收敛的。例如,在一个 3 目标归档集中,设当前第一个目标值最大的向量为 z 1 = ( 5 , 2 , 7 ) z^1 = (5, 2, 7) z1=(5,2,7) 若在下一个时间产生了一 个向量 z 2 = ( 6 , 4 , 5 ) z^2=(6, 4, 5) z2=(6,4,5),则向量 z 2 z^2 z2 将被接收进入归档集,并将第一个目标的上边界从 5 修改为 6;若接下来产生了一个向量 z 3 = ( 5 , 3 , 4 ) z^3 = (5, 3, 4) z3=(5,3,4),因 z 3 z^3 z3 支配 z 2 z^2 z2,故接收 z 3 z^3 z3,并将 z 2 z^2 z2 从归档集中移出,同时将第一个目标的上边界从 6 改为 5。如果这种进入和移出操作循环发生,第 一个目标的上边界就不会收敛。
\quad\quad 为使网格的上边界收敛,有必要做一些限制。
\quad\quad 条件 5.1 \quad ∀ k , ∄ z ∈ C ( Z ∗ ) , z k ≥ m a x z k , Z ∗ , ∃ z ∗ ∈ Z ∗ , z k ∗ = m a x z k , Z ∗ , z ∽ z ∗ \forall k, \not \exists z \in C(Z^*),z_k ≥ maxz_{k, Z^*},\exists z^* \in Z^*,z_k^* = maxz_{k, Z^*},z \backsim z^* ∀k,∃z∈C(Z∗),zk≥maxzk,Z∗,∃z∗∈Z∗,zk∗=maxzk,Z∗,z∽z∗。 这里 C ( Z ∗ ) = Z \ Z ∗ , r C(Z^*) = Z \backslash Z^*,r C(Z∗)=Z\Z∗,r 为目标数
\quad\quad 条件5.1 做岀的限制是,不存在这样的支配向量,它在某个目标上的值大于等于非支配 向量在这个目标上的最大值,同时它又与这个具有最大目标值的向量不可比较。
\quad\quad 引理 5.9 \quad 如果条件 5.1 成立,同时在时间 t t t 产生了一个向量 z ∗ ∈ Z ∗ , k ∈ { 1 , 2 , . . . , r } , z k ∗ = m a x z k , Z ∗ , z^* \in Z^*,k \in \{1, 2, ..., r\},z_k^* = maxz_{k, Z^*}, z∗∈Z∗,k∈{1,2,...,r},zk∗=maxzk,Z∗, 则有 m a x z k , M t = m a x z k , Z ∗ maxz_{k, M_t} = maxz_{k, Z^*} maxzk,Mt=maxzk,Z∗。这里 r r r 为目标数。

\quad\quad 引理 5.10 \quad 如果条件 5.1 成立, k ∈ { 1 , 2 , . . . , r } , ∃ z ∈ M t m , z k = m a x z k , Z ∗ k \in \{1, 2, ..., r\},\exists z \in M_{t_m}, z_k = maxz_{k, Z^*} k∈{1,2,...,r},∃z∈Mtm,zk=maxzk,Z∗ ,则 ∀ t > t m , ∃ y ∈ M t , y k = m a x z k , Z ∗ \forall t > t_m,\exists y \in M_t,y_k = maxz_{k, Z^*} ∀t>tm,∃y∈Mt,yk=maxzk,Z∗。 这里 r r r 为目标数。

\quad\quad 定理 5.6 \quad 如果条件5.1 成立,网格的上边界 u b k , t ub_{k, t} ubk,t 收敛 ( k ∈ { 1 , 2 , . . . , r } k \in \{1, 2, ..., r\} k∈{1,2,...,r}), r r r 为目标数。

\quad\quad 下面讨论在 2 目标的特殊情况下,条件 5.1 总是成立的
\quad\quad 定理 5.7 \quad 当目标数 r = 2 r = 2 r=2 时,条件5.1 成立
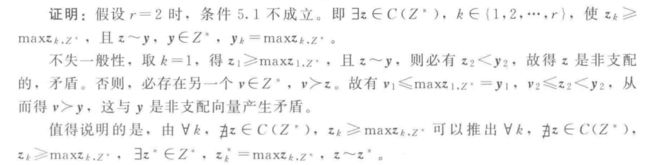
3. MOEA 的收敛性分析
\quad\quad 前面已讨论了,通过建立多目标进化的简单模型,针对具体的 reduce 函数,论证了其收敛性。最大的特点是,算法在有限步内收敛,因此具有很好的实用价值。但不足之处是不具有一般性,为此,本节从一般意义上讨论 MOEA 的收敛性。
3.1 Pareto 最优解集的特征
\quad\quad 在单目标优化 EA 中。任意两个目标函数值均可以比较其大小,因此可行解集合是全序的。而在多目标优化 MOEA 中,存在一些个体,它们之间是不可比较的,如所有的非支配个体(或向量)之间是相互不可比较的。多目标优化的可行解集是一个偏序集。
\quad\quad 定义 5.29 (关系) \quad 令 x , y ∈ X , x,y \in X, x,y∈X, R R R 为定义在 x x x 和 y y y 上的二元关系,即存在序偶 ⟨ x , y ⟩ ∈ R , \langle x, y \rangle \in R, ⟨x,y⟩∈R, 表示为 x R y xRy xRy。 若 ∀ x ∈ X , x R x \forall x \in X,xRx ∀x∈X,xRx, 则称 R R R 为自反的。若 ∀ x ∈ X , ⟨ x , x ⟩ ∉ R \forall x \in X,\langle x, x \rangle \not \in R ∀x∈X,⟨x,x⟩∈R, 则称 R R R 为反自反的。若 ∀ x , y ∈ X , x R y , \forall x,y \in X,xRy, ∀x,y∈X,xRy, 则必有 y R x , yRx, yRx, 称 R R R 为对称的。若 ∀ x , y ∈ X , x R y , y R x , \forall x,y \in X,xRy,yRx, ∀x,y∈X,xRy,yRx, 则必有 x = y , x =y, x=y, 称 R R R 为反对称的。若 ∀ x , y ∈ X , x R y , y R z , \forall x,y \in X,xRy,yRz, ∀x,y∈X,xRy,yRz, 则必有 x R z , xRz, xRz, 称 R R R 为传递的。
\quad\quad 定义 5.30 (偏序关系和偏序集) \quad 若 R R R 是自反的、反对称的和传递的,则称 R R R 为偏序关系,同时称 ( X , R ) (X, R) (X,R) 为偏序集。
\quad\quad 定义 5.31 (严格偏序关系) \quad 若 R R R 是反自反的、传递的,则称 R R R 为严格偏序关系。
\quad\quad 在定义 5.31 中没有列出反对称关系,是因为由反自反和传递的这两个关系,可以推导岀反对称关系。在多目标优化中定义的支配关系 “ ≻ ” “\succ” “≻” 是严格偏序关系,称 ( X , ≻ ) (X, \succ) (X,≻) 为偏序集。
\quad\quad 定义 5.32 (最小元素) \quad 称 x ∗ x^* x∗ 是偏序集 ( X , ≻ ) (X, \succ) (X,≻) 中的最小元素,若在 X X X 中不存在任何其他 x x x 比 x ∗ x^* x∗ 更小,即 ∄ x ∈ X , \not \exists x \in X, ∃x∈X, 使 x ≻ x ∗ x \succ x^* x≻x∗。 所有最小元素的集合表示为 M ( X , ≻ ) M(X, \succ) M(X,≻)。
\quad\quad 这里定义的最小元集合 M ( X , ≻ ) M(X, \succ) M(X,≻),就是 X X X 的非支配集。
\quad\quad 一般情况下,有 X = R n X = R^n X=Rn,但在 M O E A MOEA MOEA 实现和应用中,所有的操作或运算都是基于有限集合的,通常将这个有限集合称为可行解集。在任何有限解集上,至少存在一个最优解。
\quad\quad 定理 5.8 \quad 给定一个多目标优化问题 MOP (multi-objective problem)和非空有限可行解集 w ⊆ Ω w \subseteq \Omega w⊆Ω, 至少存在一个最优解

\quad\quad 定义 5.33 (variation kernel, VK) \quad 在 E A EA EA 中, V K VK VK 是一个函数,它将搜索空间中父个体的转移概率映射到其子个体。当 V K > 0 VK>0 VK>0,表明 V K VK VK 是正的,即 PVK( positive variation kernel)
\quad\quad Rudolph 定义的 V K VK VK,即转移概率函数,就是可达条件。也就是说,通过合适的交叉和变异操作,使搜索空间中每个点(个体)均成为可访问的。这样,在有限时间内,至少有一个个体进入到偏序集中。
\quad\quad 定理 5.9 \quad 在有限搜索空间中,一个具有 P V K PVK PVK 和最优个体选择策略的 M O E A MOEA MOEA,在进化过程中产生了一个群体序列 P k n o w n ( t ) P_{known}(t) Pknown(t),至少有一个个体在有限时间内以概率 1 1 1 进入偏序集中。
\quad\quad 定理 5. 10 (充分条件) \quad 如果一个 M O E A MOEA MOEA 的 V K VK VK 是正的,则在有限时间内以概率 1 1 1 使组成群体 P k n o w n P_{known} Pknown 的个体均为最小元素。
\quad\quad 定理 5.11 \quad 任何 M O P MOP MOP 的 P a r e t o Pareto Pareto 最优边界 P F t r u e PF_{true} PFtrue 最多由无穷个不可数的向量组成。
\quad\quad 在讨论 M O P MOP MOP 时, P F t r u e PF_{true} PFtrue 的界是一个有很意义的概念,定理 5.8 给出了其下界为 1 1 1,定理 5.12 将给出其上界。我们可以用 B o x Box Box 计数来定义最优边界的维数。
\quad\quad 定义 5.34 (Box 计数维数) \quad 在空间 R k R^k Rk 中,一个有界集 S S S 的 B o x Box Box 计数维数定义为:
B o x d i m ( S ) = lim ϵ → 0 l n N ( ϵ ) l n ( 1 / ϵ ) Boxdim(S) = \lim_{\epsilon \to 0} \frac {lnN(\epsilon)}{ln(1/\epsilon)} Boxdim(S)=ϵ→0limln(1/ϵ)lnN(ϵ)
式中, N ( ϵ ) N(\epsilon) N(ϵ) 为与 S S S 相交(intersect)的 Box 的数目,且极限存在。
\quad\quad 定理 5.12 \quad 给定一个 MOP 及其 Pareto 最优边界 P F t r u e , PF_{true}, PFtrue, 如果 P F t r u e PF_{true} PFtrue 是有界的,则它是一个 Box 计数维数不大于 q — 1 集合。

3.2 MOEA 的收敛性
\quad\quad 为了讨论 MOEA 的收敛性,先回顾一下单目标情况下 EA 的收敛性。设 x x x 为决策变量, I I I 为决策变量空间, F F F 为适应度函数, t t t 为进化代数。当满足条件:
\quad\quad ① ∀ x , y ∈ I , \forall x,y \in I, ∀x,y∈I, y y y 为 x x x 通过进化操作所得(即可达性)
\quad\quad ② 群体进化序列 P ( 0 ) , P ( 1 ) , … , P(0), P(1),…, P(0),P(1),…, 是单调的,即
∀ t : m i n { F ( x ( t + 1 ) ∣ x ( t + 1 ) ∈ P ( t + 1 ) ) } ≤ m i n { F ( x ( t ) ∣ x ( t ) ∈ P ( t ) ) } \forall t:min\{F(x(t +1)|x(t + 1) \in P(t +1))\} ≤ min\{F(x(t)|x(t)\in P(t))\} ∀t:min{F(x(t+1)∣x(t+1)∈P(t+1))}≤min{F(x(t)∣x(t)∈P(t))}
\quad\quad Back 证明了 E A EA EA 将以概率 1 1 1 收敛
\quad\quad 在多目标情况下,以上两个条件都不合适。一方面,单目标优化时,可行解集是全序的,而多目标优化时可行解集是偏序的;另一方面,基于 Pareto 的适应度的计算不同于单目标函数的适应度,它在不同进化代可能具有不同的值;第三个方面,多目标优化的解个体是一个向量,而且最后的结果是一个解集。
\quad\quad MOEA 的收敛过程是通过 P F k n o w n PF_{known} PFknown 不断逼近 P F t r u e PF_{true} PFtrue 实现的,为了描述不同进化代之间的关系,下面给出有关定义
\quad\quad 定义 5.35 \quad 给定一个 MOP 以及其进化群体 P A PA PA 和 P B PB PB,定义 P A PA PA 和 P B PB PB 的关系为 P A ≥ P B PA ≥ PB PA≥PB,若满足条件 ∀ x ∈ P A , ∄ y ∈ P B , \forall x \in PA,\not \exists y \in PB, ∀x∈PA,∃y∈PB, 使 y ≻ x y \succ x y≻x。 \quad ( P i P_i Pi:表示第 i i i 代进化群体序列)
\quad\quad 定义 5.35 表明,若 P A ≥ P B PA ≥ PB PA≥PB, 则在 P A PA PA 中不存任何受 P B PB PB 所支配的向量,但在 P B PB PB 中可能存在受 P A PA PA 所支配的向量。由此可知 P k n o w n ( t + 1 ) ≥ P k n o w n ( t ) P_{known}(t +1) ≥ P_{known}(t) Pknown(t+1)≥Pknown(t),因为 P k n o w n ( t + 1 ) = N D ( P k n o w n ( t ) ∪ P c u r r e n t ( t + 1 ) ) = { x ∈ P k n o w n ( t ) ∪ P k n o w n ( t + 1 ) ∣ ∄ y ∈ P k n o w n ( t ) ∪ P c u r r e n t ( t + 1 ) , P_{known}(t +1) = ND(P_{known}(t) \cup P_{current}(t +1)) = \{x \in P_{known}(t) \cup P_{known}(t + 1) | \not \exists y \in P_{known}(t) \cup P_{current}(t +1) , Pknown(t+1)=ND(Pknown(t)∪Pcurrent(t+1))={x∈Pknown(t)∪Pknown(t+1)∣∃y∈Pknown(t)∪Pcurrent(t+1), 使 y ≻ x } y \succ x\} y≻x}
\quad\quad 定理 5.13 \quad 给定 MOP 和 MOEA,若满足条件:
\quad\quad ① Pareto 最优边界的 Box 计数维数不大于 r − 1 , r r-1, r r−1,r 为目标数。
\quad\quad ② P k n o w n ( 0 ) , P k n o w n ( 1 ) , . . . P_{known}(0),P_{known}(1),... Pknown(0),Pknown(1),... 是单调的,即
∀ t : P k n o w n ( t + 1 ) ≥ P k n o w n ( t ) \forall t : P_{known}(t + 1) ≥ P_{known}(t) ∀t:Pknown(t+1)≥Pknown(t)
即 MOEA 以概率 1 1 1 收敛,即
P r o b ( lim t → ∞ { P t r u e = P ( t ) } ) = 1 P_{rob}(\lim_{t \to \infty}\{P_{true} = P(t)\}) = 1 Prob(t→∞lim{Ptrue=P(t)})=1
式中, P r o b ( ) 为概率, P_{rob}() 为概率, Prob()为概率, P ( t ) = P k n o w n ( t ) , P t r u e P(t) = P_{known}(t),P_{true} P(t)=Pknown(t),Ptrue 为 全局 Pareto 最优解集。
\quad\quad 定理 5.14 \quad 如果定理 5.9 成立,且在 P k n o w n ( t ) P_{known}(t) Pknown(t) 中的最小元是其父代个体的组合并产生子代个体,则进化群体将收敛到 Pareto 最优解集 P t r u e P_{true} Ptrue
\quad\quad Rudolph 的收敛理论中,除基于 VK 外(如定理 5.14),他还提出了基于相似随机矩阵的方法。
\quad\quad 定义 5.36 \quad G G G 是一个随机矩阵(stochastic matrix), 它记录了从当前进化群体到下一 代的转移概率,即从 P c u r r e n t ( t ) P_{current}(t) Pcurrent(t) 到 P c u r r e n t ( t + 1 ) P_{current}(t+1) Pcurrent(t+1) 的转移概率
\quad\quad 定义 5.37 (收敛) \quad 如果当 t → ∞ t \to \infty t→∞ 时, P F t r u e PF_{true} PFtrue 与 P F k n o w n ( t ) PF_{known}(t) PFknown(t) 之间的距离以概率 1 1 1 趋向于 0 0 0,即
\quad\quad 当 t → ∞ t \to \infty t→∞ 时, ∣ P F t r u e ∪ P F k n o w n ( t ) ∣ − ∣ P F t r u e ∩ P F k n o w n ( t ) ∣ → 0 |PF_{true} \cup PF_{known}(t)| - |PF_{true} \cap PF_{known}(t)| \to 0 ∣PFtrue∪PFknown(t)∣−∣PFtrue∩PFknown(t)∣→0
或
\quad\quad 当 t → ∞ t \to \infty t→∞ 时, ∣ P F k n o w n ( t ) ∣ − ∣ P F t r u e ∪ P F k n o w n ( t ) ∣ → 0 |PF_{known}(t)| - |PF_{true} \cup PF_{known}(t)| \to 0 ∣PFknown(t)∣−∣PFtrue∪PFknown(t)∣→0
则称 MOEA 收敛。
\quad\quad 定理 5.15 \quad 设 G G G 是一个相似随机矩阵,它记录了从 P c u r r e n t ( t ) P_{current}(t) Pcurrent(t) 到 P c u r r e n t ( t + 1 ) P_{current}(t+1) Pcurrent(t+1) 的转移概率。对于给定的 MOEA,如果 G G G 是正定的,则 M O E A MOEA MOEA 收敛。
\quad\quad 如果将当前代的所有最小元都选入到下一代,则会使进化群体变得越来越大。在实际应中,往往只选取一部分有代表性的最小元进入下一代进化群体。
\quad\quad 定理 5.16 \quad 设 G G G 是一个相似随机矩阵,它记录了从 P c u r r e n t ( t ) P_{current}(t) Pcurrent(t) 到 P c u r r e n t ( t + 1 ) P_{current}(t+1) Pcurrent(t+1) 的转移概率。对于给定的 MOEA,每一代进化时从 P c u r r e n t ( t ) P_{current}(t) Pcurrent(t) 中选取一部分具有代表性的最小元 进入 P c u r r e n t ( t + 1 ) P_{current}(t+1) Pcurrent(t+1),如果 G G G 是正定的,则 MOEA 收敛
\quad\quad 推论 5.2 \quad F F F 是给定 M O P MOP MOP 的目标向量函数,针对定理 5.15 的情况(即上一代最小元无限制地进入下一代),则进化群体以概率 1 1 1 收敛到 Pareto 最优解集,同时进化群体的规模以概率 1 1 1 收敛到预定的最小值或 P t r u e P_{true} Ptrue 的势(即 ∣ P t r u e ∣ |P_{true}| ∣Ptrue∣)
\quad\quad 推论 5.3 \quad F F F 是给定 MOP 的目标向量函数,针对定理 5.16 的情况(即限定进化群体规模,每次只从上一代选取一定数量的,且有代表性的最小元进入下一代),则进化群体以概率 1 1 1 收敛到 Pareto 最优解集的子集。
\quad\quad 值得说明的是,根据定义 5.37、定理 5.15 和定理 5.16 所指的收敛是从目标向量方面考虑的,而推论 5.2 和推论 5.3 则是从决策向量方面考虑的
\quad\quad 本节讨论的收敛理论主要基于两个假设:一是搜索空间是可数的;二是 Pareto 最优解集的势是有限的。Hanne 基于锥(cone)理论,针对连续函数提出了 MOEA 收敛理论。
