NNDL 作业6 卷积
一、概念
（一）卷积
（1）什么叫卷积
卷积、旋积或褶积(英语：Convolution)是通过两个函数f和g生成第三个函数的一种数学运算，其本质是一种特殊的积分变换，描述一个函数和另一个函数在某个维度上的加权“叠加”作用，学术语言也就是：表征函数f与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。
文来自卷积核_百度百科 (baidu.com)
（2）卷积的类别
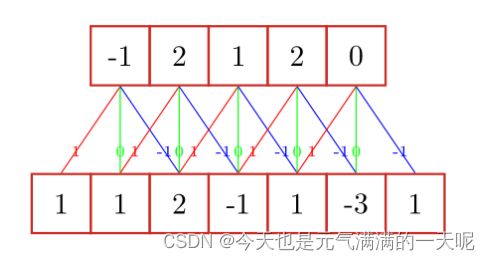
1）一维卷积：在一维数据上进行滑动窗口操作并进行加权求和。
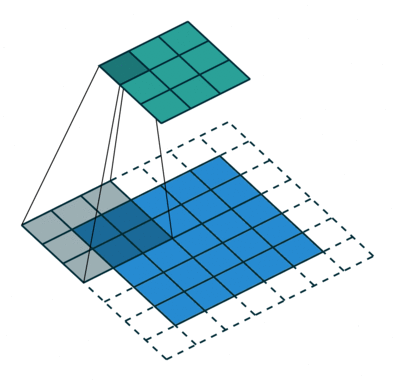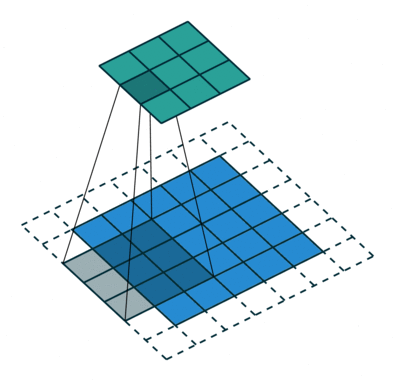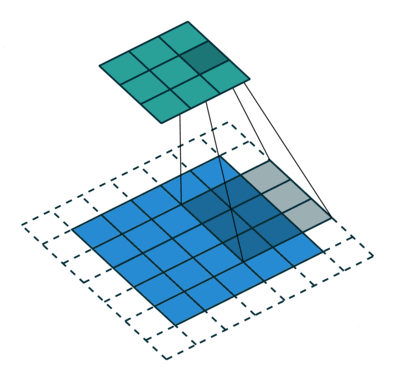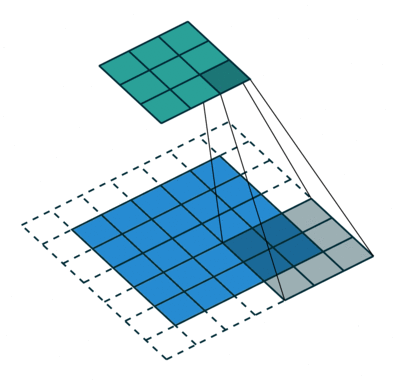
2）二维卷积：在二维图像上进行滑动窗口操作并进行加权求和。
二维卷积中又包含单通道卷积和多通道卷积，下图为一个单通道卷积
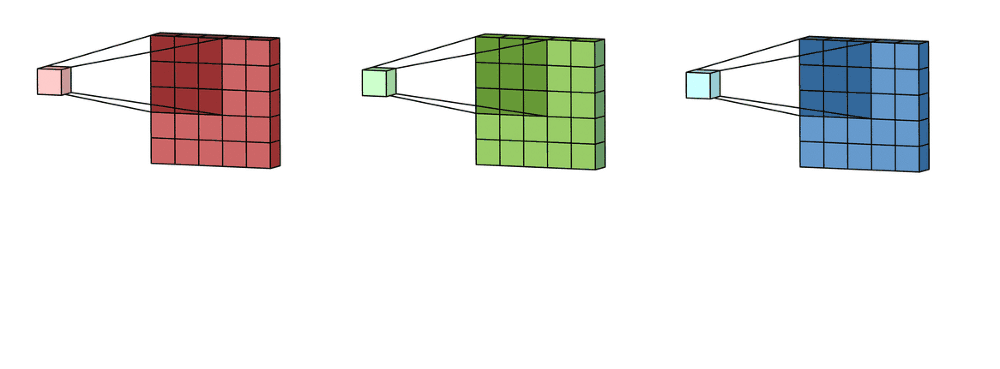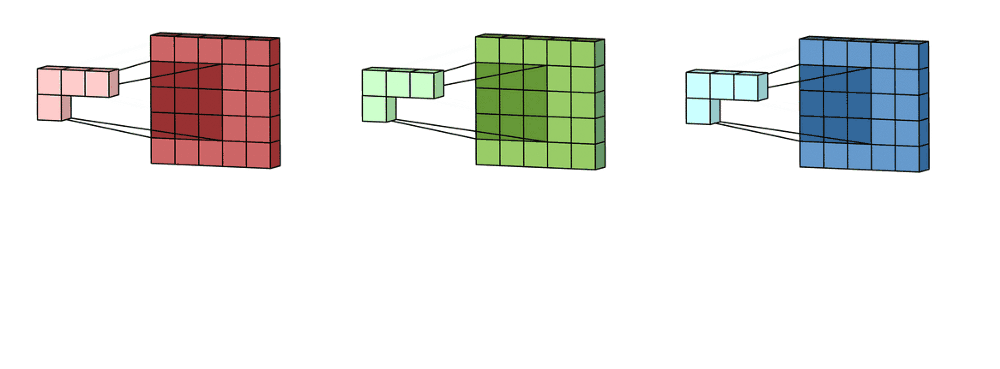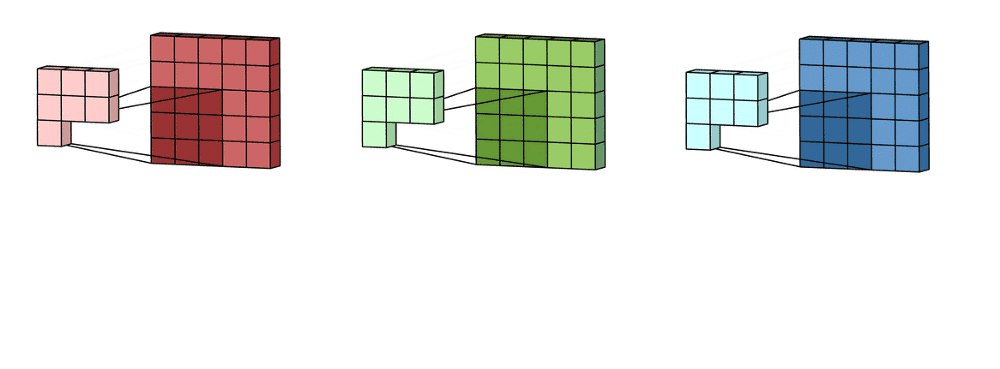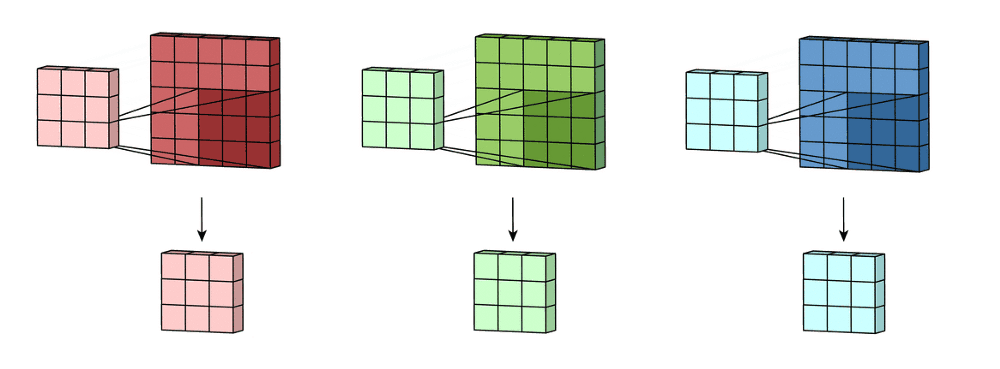
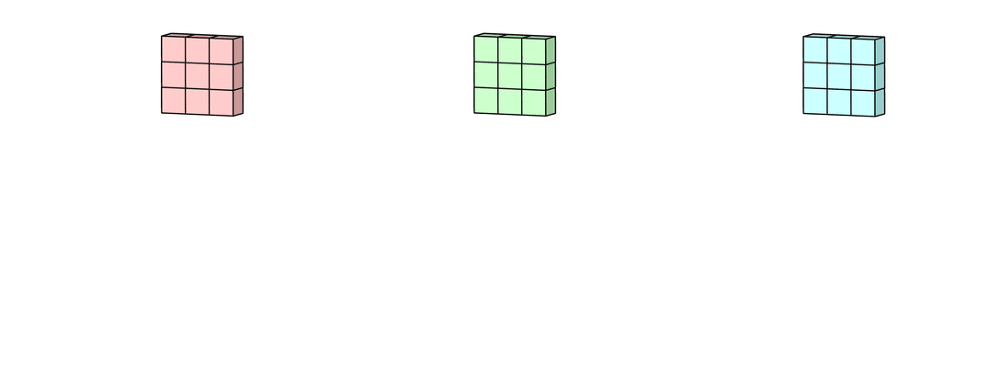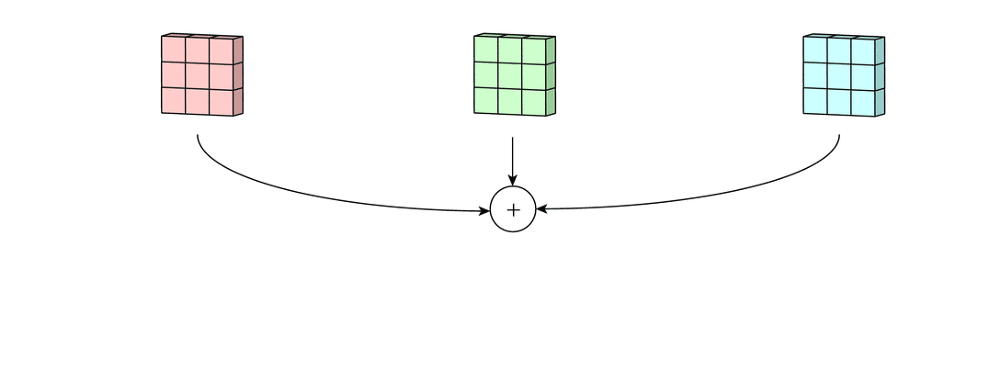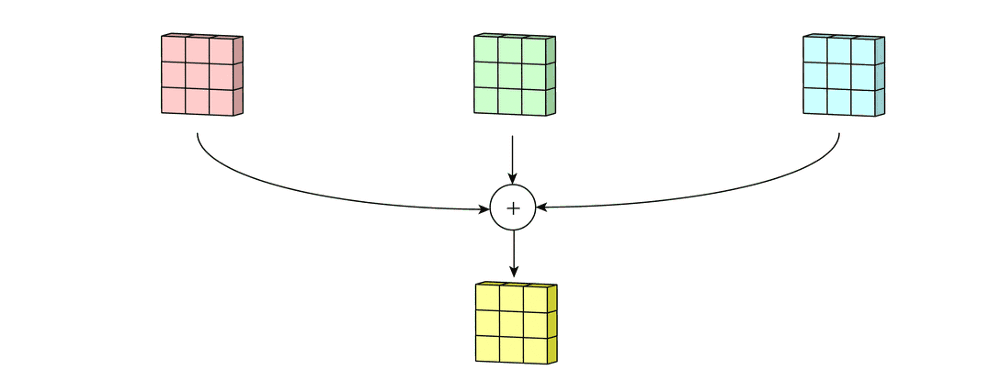
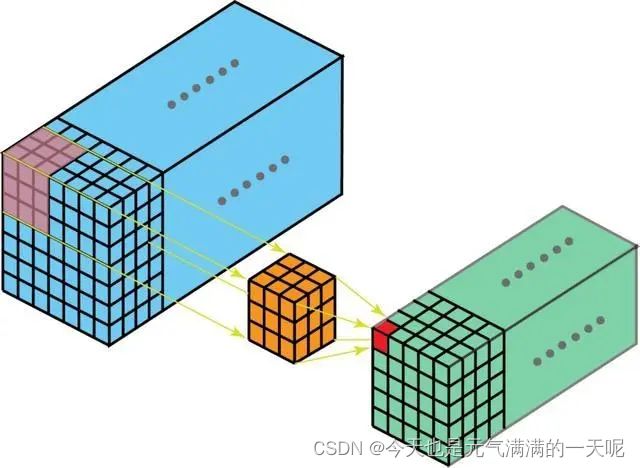
多通道卷积：卷积神经网络中每层用多个滤波器核就是多通道，比如RGB图像。
首先过滤器中的每个内核分别应用于输入层中的三个通道,并相加；然后，执行三次卷积，产生3个尺寸为3×3的通道。
然后将这三个通道相加在一起（逐元素加法）以形成一个单通道。
3）3D卷积
所有3个方向（图像的高度，宽度，通道）上移动。在每个位置，逐元素乘法和加法提供一个数字。由于滤镜滑过3D空间，因此输出数字也排列在3D空间中，然后输出是3D数据。
5）转置卷积（解卷积、反卷积）
6）扩张卷积
来自形象理解深度学习中八大类型卷积 (baidu.com)
（3）卷积的作用
1）特征提取：卷积可以通过滤波器提取出信号中的特征，比如边缘、纹理等。这些特征对于图像分类和识别任务非常重要。
2）降维：卷积可以通过池化操作减小图像的尺寸，从而降低数据的维度。这对于处理大规模图像和文本数据非常有用。
3）去噪：卷积可以通过滤波器去除信号中的噪声。这在信号处理和图像处理领域中非常常见，有助于提高数据的质量。
4）图像增强：卷积可以通过一些滤波器对图像进行增强，比如锐化、平滑等。这有助于提高图像的视觉效果和品质。
【来自卷积的作用与意义 - 飞桨AI Studio星河社区 (baidu.com)】
（二）卷积核
（1）什么是卷积核
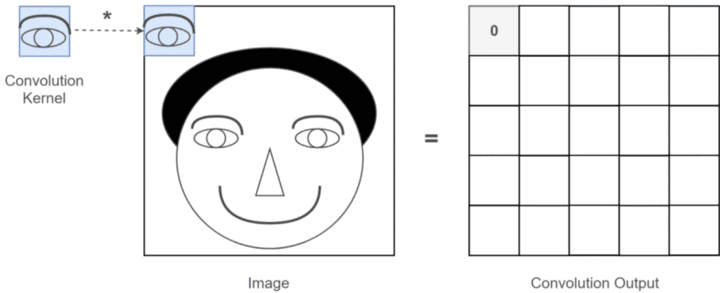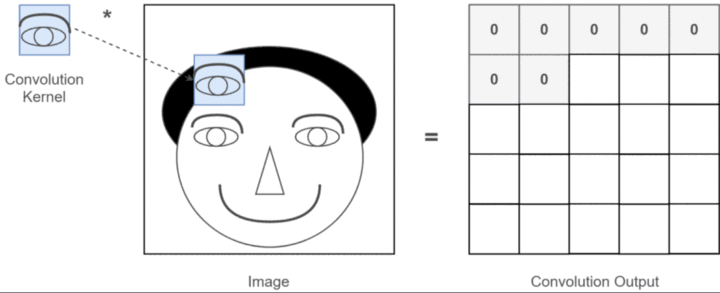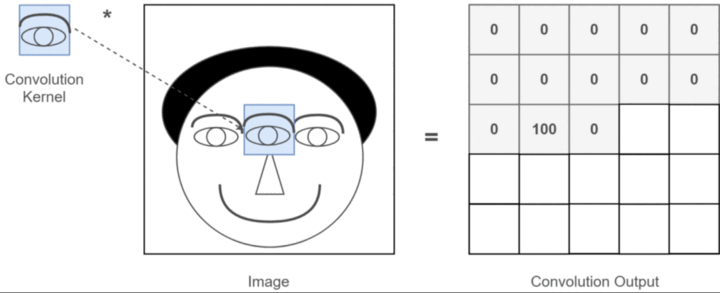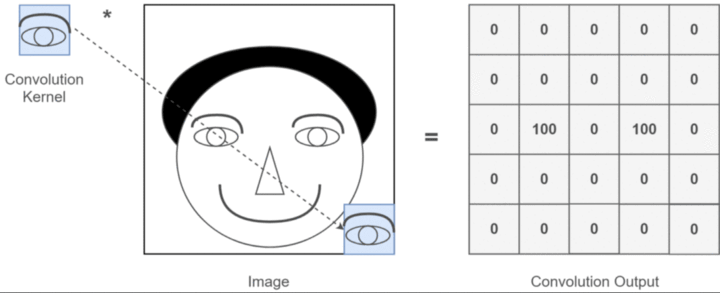
卷积核就是图像处理时，给定输入图像，输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素，其中权值由一个函数定义，这个函数称为卷积核。
在卷积神经网络里，卷积核其实就是一个过滤器，但在深度学习里，它不做反转，而是直接执行逐元素的乘法和加法，我们把这个又称为互相关，在深度学习里称为卷积。
卷积核_百度百科 (baidu.com)
（2）卷积核都有什么
一个卷积核一般包括核大小(Kernel Size)、步长(Stride)以及填充步数(Padding)。
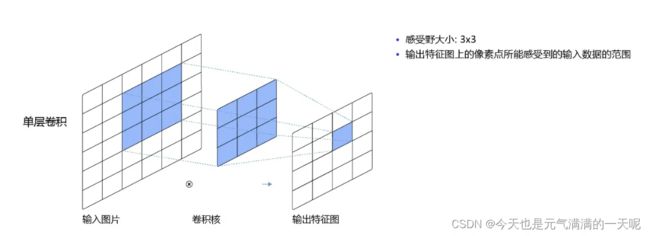
核大小：定义了卷积的大小范围，在网络中代表感受野的大小。一般情况下，卷积核越大，感受野越大，看到的图片信息越多，所获得的全局特征越好。但大的卷积核会导致计算量的暴增，计算性能也会降低。
步长：步长代表提取的精度, 步长定义了当卷积核在图像上面进行卷积操作的时候，每次卷积跨越的长度。
填充：卷积核与图像尺寸不匹配，会造成了卷积后的图片和卷积前的图片尺寸不一致，为了避免这种情况，需要先对原始图片做边界填充处理。
（3）卷积核能做什么
卷积核可以提取图像的局部特征，生成一个个神经元，再经过深层的连接，就构建出了卷积神经网络。
它通过滑动窗口的方式在输入数据上进行卷积操作，提取出不同位置的局部特征，并生成对应的特征图。这些特征图包含了输入数据的不同抽象层次的特征信息，具有重要的表征能力。
来自【23-24 秋学期】NNDL 作业6 卷积-CSDN博客 CICC科普栏目｜卷积核的基本概况 (qq.com)
（三）特征图
卷积神经网络的重要组件之一是特征图，它是通过对图像应用卷积滤波器生成的输入图像的表示。
通俗来说，特征图是卷积神经网络中卷积层的输出。它们是二维数组，包含卷积滤波器从输入图像或信号中提取的特征。
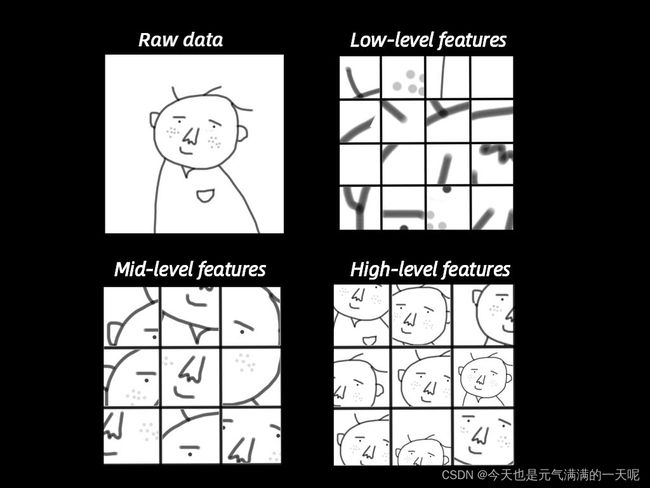
随着层数的增加，网络能够学习越来越复杂和抽象的特征。通过结合来自多层的特征，网络可以识别输入数据中的复杂模式，并做出准确的预测。
如下图所示【图来自白话版，聊聊“深度学习” (qq.com)】
【文部分来自可视化CNN和特征图 (baidu.com)】
（四）特征选择
图来自【精选】卷积神经网络工作原理的直观理解_nvidia sparse convolution 原理_superdont的博客-CSDN博客
（1）什么是特征选择？
特征选择旨在通过去除不相关、冗余或嘈杂的特征，从原始特征中选择一小部分相关特征。特征选择过程基于从特征向量中选择最一致、相关和非冗余的特征子集。
（2）特征选择的好处
特征选择通常可以带来更好的学习性能、更高的学习精度、更低的计算成本和更好的模型可解释性。它不仅减少了训练时间和模型复杂性，而且最终有助于防止过度拟合。
（3）特征选择技术
监督方法：可以识别相关特征以最好地实现监督模型的目标（例如分类或回归问题），并且它们依赖于标记数据的可用性。
半监督方法：当一小部分数据被标记时，我们可以利用半监督特征选择，它可以同时利用标记数据和未标记数据。
无监督方法：忽略目标变量，例如使用相关性去除冗余变量的方法。
文来自特征选择——详尽综述 - 知乎 (zhihu.com)
（五）步长
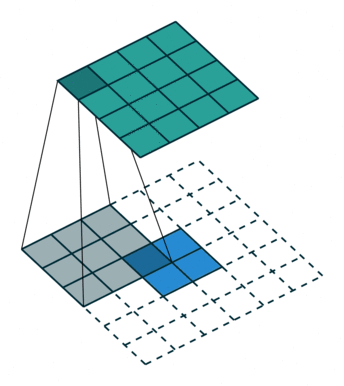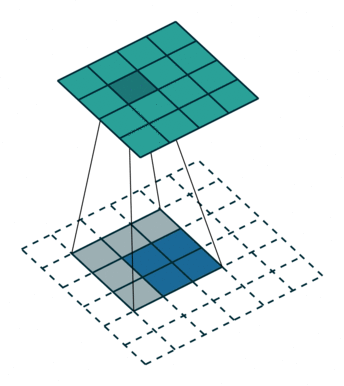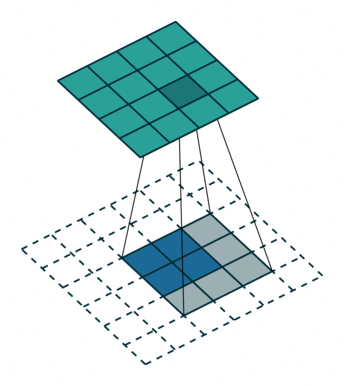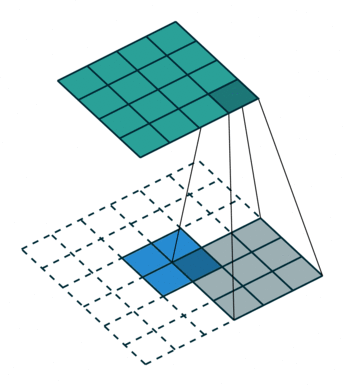
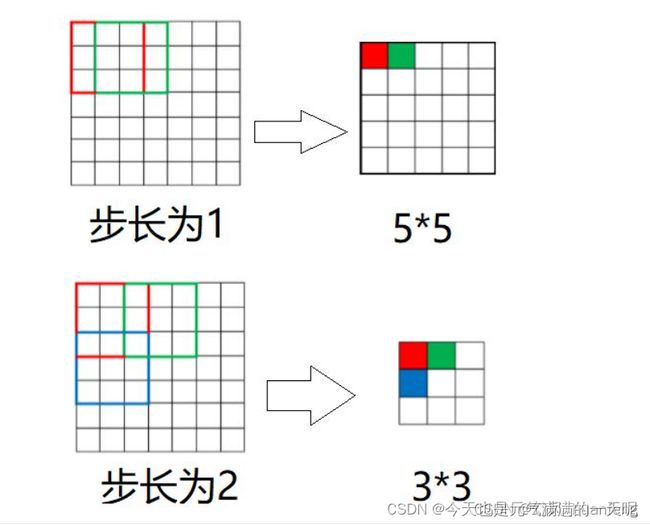
步长简单来说就是是行/列的滑动步数，是卷积核的重要组成部分之一，在前文中也提到了这一概念。
下图来自计算机视觉：卷积步长(Stride)_幻风_huanfeng的博客-CSDN博客
（六）填充
（1）填充是什么
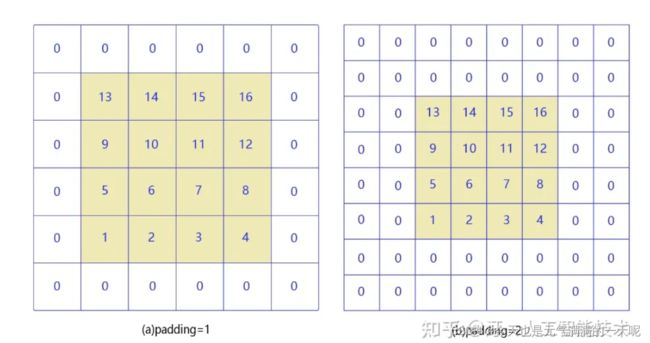
填充是指在边缘像素点周围填充数，使得输入图像的边缘像素也可以参与卷积计算。其中常用的有零填充，也就是在输入周围添加0。
如下图所示【图文来自深度学习基础入门篇[9.1]：卷积之标准卷积：卷积核/特征图/卷积计算、填充、感受视野、多通道输入输出、卷积优势和应用案例讲解 - 知乎 (zhihu.com)】：
（2）为什么填充
1.由于输入图像边缘位置的像素点无法进行卷积滤波，进行填充可以减少边缘信息丢失，使边缘像素也参与卷积滤波。
2.使得输入输出图像尺寸一致
（七）感受野
（1）什么是感受野
（2）感受野的特点
- 感受野越大，说明其接触的原始图像的范围越大，意味着其包含着更加全局、语义信息更丰富的特征；
- 感受野越小，说明其包含的特征更关注局部细节；
- 感受野不受padding的影响，sripe会影响下一层的感受野。
文来自卷积神经网络的感受野(receptive field) - Liang-ml - 博客园 (cnblogs.com)
二、探究不同卷积核的作用
卷积神经网络工作原理的直观理解_superdont的博客-CSDN博客
（图1）
（图二） 
（图三）
（一）图1分别使用卷积核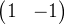
，
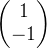输出特征图
（2）代码
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from PIL import Image
import matplotlib.pyplot as plt
file_path = 'tu1.png'
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False
im = Image.open(file_path).convert('L') # 读入一张灰度图的图片
im = np.array(im, dtype='float32') # 将其转换为一个矩阵
# 定义（-1，1）卷积核
kernel = np.array([[-1, 1]])
#定义（-1，1）.T卷积核
kerne2=np.array([[-1,1]]).T
plt.imshow(im.astype('uint8'), cmap='gray') # 可视化图片
plt.title('原图')
plt.show()
# 执行卷积操作
feature_map1 = np.zeros(im.shape)
feature_map2 = np.zeros(im.shape)
for i in range(im.shape[0]):
for j in range(im.shape[1] - 1):
patch = im[i, j:j+2]
feature_map1[i, j+1] = np.sum(patch * kernel)
# 可视化特征图
plt.imshow(feature_map1, cmap='gray')
plt.title('（-1，1）的特征图')
plt.show()
for i in range(im.shape[0]):
for j in range(im.shape[1]-1):
patch=im[i,j:j+2]
feature_map2[i,j+1]=np.sum(patch*kerne2)
# 可视化特征图
plt.imshow(feature_map2, cmap='gray')
plt.title('（-1，1）.T的特征图')
plt.show()
后发现每次都进行一次卷积和的计算太麻烦，接改成了convolve函数：
def convolve(im, kernel):
# 执行卷积操作
feature_map = np.zeros(im.shape)
for i in range(im.shape[0]):
for j in range(im.shape[1] - 1):
patch = im[i, j:j+2]
feature_map[i, j+1] = np.sum(patch * kernel)
return feature_map（2）实验结果
（3）修正
后来看到了学长【精选】NNDL 作业5：卷积_cmap='gray-CSDN博客 ，生成的照片相比较更好
代码改为：
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image, ImageFilter
# 生成图片
pic = np.zeros((7,6))
pic[:,3:6]=255
print(pic)
plt.imshow(pic,cmap='Greys_r')
plt.title('原图')
plt.show()
# 转换为灰度图像并进行卷积操作并可视化特征图
im = Image.fromarray(pic.astype('uint8'))
im = im.convert('L')
im = np.array(im, dtype='float32')
def convolve(im, kernel):
# 执行卷积操作
feature_map = np.zeros(im.shape)
for i in range(im.shape[0]):
for j in range(im.shape[1] - 1):
patch = im[i, j:j+2]
feature_map[i, j+1] = np.sum(patch * kernel)
return feature_map
#卷积核1
kernel = np.array([[1, -1]])
feature_map = convolve(im, kernel)
plt.imshow(feature_map, cmap='gray')
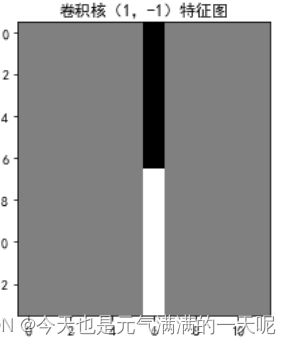
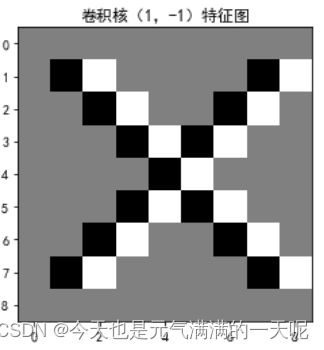
plt.title('卷积核（1，-1）特征图')
plt.show()
#卷积核2
kerne2 = np.array([[1, -1]]).T
feature_map = convolve(im, kerne2)
plt.imshow(feature_map, cmap='gray')
plt.title('卷积核（1，-1）.T特征图')
plt.show()得到的实验结果：
比从ppt中截图生成的效果更好【自己截屏的上边还有黑边边】。
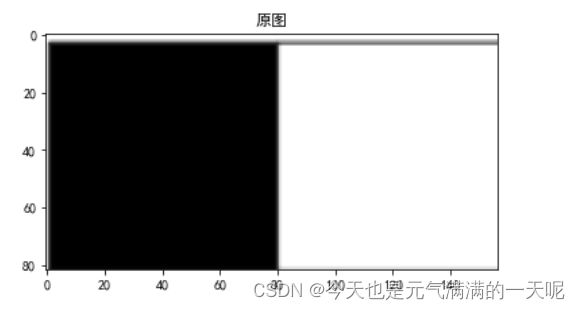
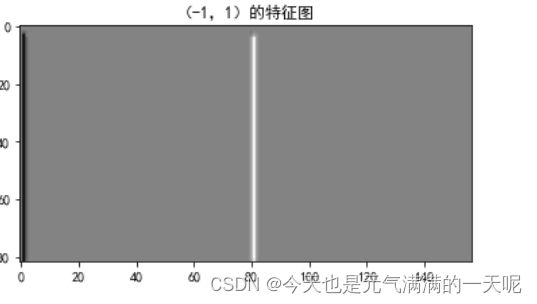
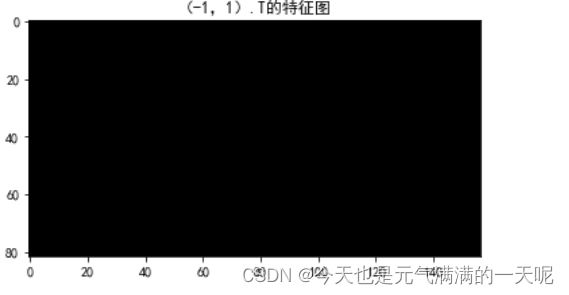
（二）图2分别使用卷积核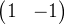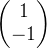，输出特征图
（1）代码
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image, ImageFilter
# 生成图片
pic = np.zeros((14,12))
pic[7:14,0:6]=255
pic[0:7,6:12]=255
plt.imshow(x,cmap='Greys_r')
plt.title('原图')
plt.show()
# 转换为灰度图像并进行卷积操作并可视化特征图
im = Image.fromarray(pic.astype('uint8'))
im = im.convert('L')
im = np.array(im, dtype='float32')
def convolve(im, kernel):
# 执行卷积操作
feature_map = np.zeros(im.shape)
for i in range(im.shape[0]):
for j in range(im.shape[1] - 1):
patch = im[i, j:j+2]
feature_map[i, j+1] = np.sum(patch * kernel)
return feature_map
#卷积核1
kernel = np.array([[1, -1]])
feature_map = convolve(im, kernel)
plt.imshow(feature_map, cmap='gray')
plt.title('卷积核（1，-1）特征图')
plt.show()
#卷积核2
kerne2 = np.array([[1, -1]]).T
feature_map = convolve(im, kerne2)
plt.imshow(feature_map, cmap='gray')
plt.title('卷积核（1，-1）.T特征图')
plt.show()（2）实验结果
（三） 图3分别使用卷积核，，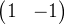
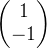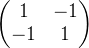，输出特征图
（1）代码
参照了一下学长的代码HBU_神经网络与深度学习 作业5 卷积_学完卷积后的作业_ZodiAc7的博客-CSDN博客，我前边都是用的numpy写的，这里改成了pytorch。
import numpy as np
import torch
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
#卷积核1
w1 = np.array([1, -1], dtype='float32').reshape([1, 1, 1, 2])
w1 = torch.Tensor(w1)
#卷积核2
w2 = np.array([1, -1], dtype='float32').T.reshape([1, 1, 2, 1])
w2 = torch.Tensor(w2)
#卷积核3
w3 = np.array([[1, -1, -1, 1]], dtype='float32').reshape([1, 1, 2, 2])
w3 = torch.Tensor(w3)
#创建卷积层
conv1 = torch.nn.Conv2d(1, 1, [1, 2])#卷积核形状为1x2：对应（1，-1）
conv1.weight = torch.nn.Parameter(w1)
conv2 = torch.nn.Conv2d(1, 1, [2, 1])#卷积核形状为2*1：对应（1，-1）.T
conv2.weight = torch.nn.Parameter(w2)
conv3 = torch.nn.Conv2d(1, 1, [2, 2])#卷积核形状为2x2,对应的是（（1，-1），（-1，1））2*2矩阵
conv3.weight = torch.nn.Parameter(w3)
# 生成图片
pic = np.zeros((9,9))
for i in range(0,7):
pic[i+1,i+1]=255
pic[i+1,7-i]=255
plt.imshow(pic,cmap='Greys_r')
plt.title('原图')
plt.show()
x = pic.reshape([1, 1, 9, 9])
x = torch.Tensor(x)
y1 = conv1(x).detach().numpy()
plt.imshow(y1.squeeze(),cmap='Greys_r')
plt.title('卷积核(1,-1)的特征图')
plt.show()
y2 = conv2(x).detach().numpy()
plt.imshow(y2.squeeze(),cmap='Greys_r')
plt.title('卷积核(-1，1)的特征图')
plt.show()
y3 = conv3(x).detach().numpy()
plt.imshow(y3.squeeze(),cmap='Greys_r')
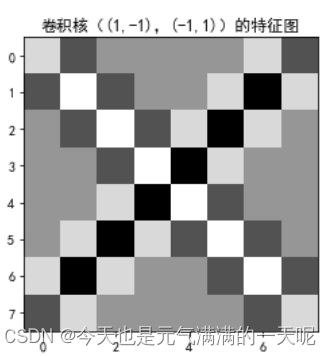
plt.title('卷积核（(1,-1)，(-1,1)）的特征图')
plt.show()（2）实验结果
（四） 实现灰度图的边缘检测、锐化、模糊。
（1）边缘检测
实验代码：
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from PIL import Image
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False
file_path = 'tu4.png'
im = Image.open(file_path).convert('L')
im = np.array(im, dtype='float32')
plt.imshow(im.astype('uint8'), cmap='gray') # 可视化图片
plt.title('原图')
plt.show()
def kernel(kernel,im,conv1):
inout_kernel=kernel.reshape((1,1,3,3))
conv1.weight.data = torch.from_numpy(inout_kernel)
edge1 = conv1(im)
#确保图像数值不超过【0，255】
for i in range(edge1.shape[2]):
for j in range(edge1.shape[3]):
if edge1[0][0][i][j] > 255:
edge1[0][0][i][j] = 255
if edge1[0][0][i][j] < 0:
edge1[0][0][i][j] = 0
x = edge1.detach().numpy().squeeze()
return x
im = np.reshape(im, (1, 1, im.shape[0], im.shape[1]))
conv1 = nn.Conv2d(1, 1, 3 ,bias=False,padding=1) # 定义边缘卷积)
#卷积核--边缘
sobel_kernel = np.array([[-1, -1, -1],
[-1, 8, -1],
[-1, -1, -1]], dtype='float32')
im = torch.from_numpy(im)
edge1 = conv1(im) # 作用在图片上
x=kernel(sobel_kernel,im,conv1)
plt.imshow(x, cmap='gray')
plt.title('边缘检测')
plt.show()实验结果：
实验代码及处理灰度图参照【精选】NNDL 作业5：卷积_cmap='gray-CSDN博客
（2）锐化
实验代码：
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from PIL import Image
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 #有中文出现的情况，需要u'内容
file_path = 'tu4.png'
im = Image.open(file_path).convert('L') # 读入一张灰度图的图片
im = np.array(im, dtype='float32') # 将其转换为一个矩阵
print(im.shape[0], im.shape[1])
plt.imshow(im.astype('uint8'), cmap='gray') # 可视化图片
plt.title('原图')
plt.show()
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
conv1 = nn.Conv2d(1, 1, 3 ,bias=False,padding=1) # 定义卷积
#锐化卷积核
sobel_kernel = np.array([[0, -1, 0],
[-1, 5, -1],
[0, -1,0]], dtype='float32')
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3))
conv1.weight.data = torch.from_numpy(sobel_kernel)
edge1 = conv1(Variable(im)) # 作用在图片上
for i in range(edge1.shape[2]):
for j in range(edge1.shape[3]):
if edge1[0][0][i][j]>255:
edge1[0][0][i][j]=255
if edge1[0][0][i][j]<0:
edge1[0][0][i][j]=0
x = edge1.data.squeeze().numpy()
print(x.shape) # 输出大小
plt.imshow(x, cmap='gray')
plt.show()实验结果：
（3）模糊
实验代码：
# coding=gbk
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from PIL import Image
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 #有中文出现的情况，需要u'内容
file_path = 'tu4.png'
im = Image.open(file_path).convert('L') # 读入一张灰度图的图片
im = np.array(im, dtype='float32') # 将其转换为一个矩阵
print(im.shape[0], im.shape[1])
plt.imshow(im.astype('uint8'), cmap='gray') # 可视化图片
plt.title('原图')
plt.show()
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
conv1 = nn.Conv2d(1, 1, 3 ,bias=False,padding=1) # 定义卷积
#模糊
sobel_kernel = np.array([[0.0625, 0.125, 0.0625],
[0.125, 0.25, 0.125],
[0.0625, 0.125,0.0625]], dtype='float32') # 定义轮廓检测算子
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3)) # 适配卷积的输入输出
conv1.weight.data = torch.from_numpy(sobel_kernel) # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im)) # 作用在图片上
for i in range(edge1.shape[2]):
for j in range(edge1.shape[3]):
if edge1[0][0][i][j]>255:
edge1[0][0][i][j]=255
if edge1[0][0][i][j]<0:
edge1[0][0][i][j]=0
x = edge1.data.squeeze().numpy()
print(x.shape) # 输出大小
plt.imshow(x, cmap='gray')
plt.title('模糊')
plt.show()实验结果：
（五） 总结不同卷积核的特征和作用。
参考https://setosa.io/ev/image-kernels/
（1）边缘检测
卷积核：
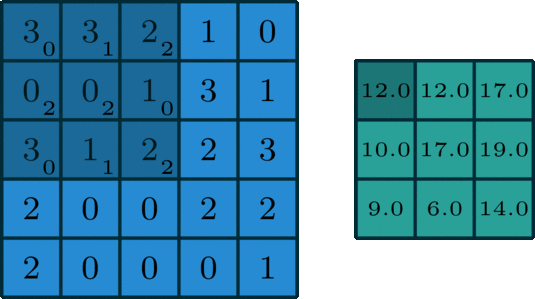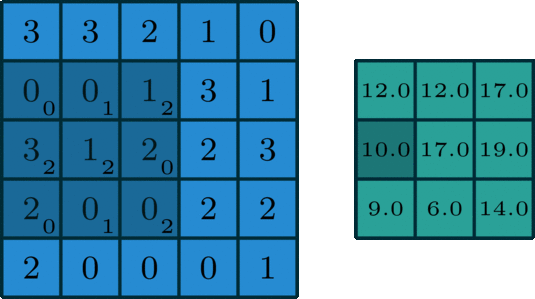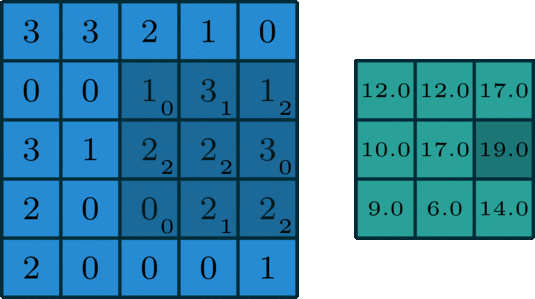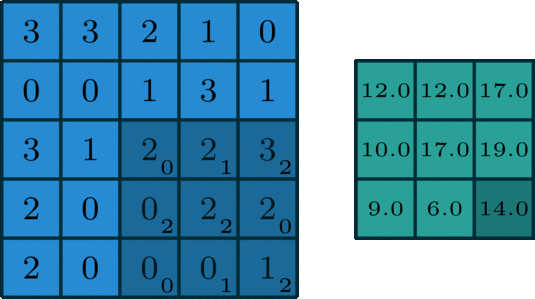
可以看到，卷积核中最大的值为8，在下图那个红框框中，可以发现，上边三个值都比较小，下边的值都比较大，也就是卷积边缘地带时，得到的卷积值比较大，最后出来的值像素色一般是白色。
对比一下下边这个红框框，此时不是边缘地带，可以发现最后的卷积值接近0，也就是偏黑色。
由此可知，边缘检测的原理：扩大卷积核中的一个数为突出值，使得边缘处两色像素值的差值大，实现对边缘特征的提取。
（2）锐化
可以看到这个红框框中心相对于其他地方偏白，中心值最大可以着重提取这个地方的白色。
锐化的原理：着重提取中心处的颜色，使其色彩更加鲜明，提高聚焦度。
（3）模糊
这个直接观察卷积核，卷积核中的值都小于0，可以减少图像中像素值差异大的点。
模糊原理：使用卷积核处理图中与周围亮度差异过大的点，减少差异，使得像素值相近、轮廓模糊。
来自【【23-24 秋学期】NNDL 作业6 卷积-CSDN博客】
三、总结
概念类的（一）已经有了详细说明了，总结中着重说一下我代码遇到的问题
（一）
开始的图1，图2，我是直接截的老师ppt里边的图，但是发现效果不太好，然后参考了学长的【在前边有注明】，使用：
pic = torch.zeros((7,6))
x=pic
pic[:,3:6]=255
print(pic)
plt.imshow(pic,cmap='Greys_r')
plt.show()生成了图像，发现效果的确要好一些。
（二）
在使用卷积核得到特征图时，最开始是直接用的numpy，使用的卷积原理（卷积核kernel和图像块patch进行元素级相乘，并使用np.sum()函数对结果进行求和，得到当前位置的特征图值。）做的【开始忘了tensor了】，在第三个实验里改为pytorch：
大概过程就是：建立三个卷积核，分别设置对应的格式：([1, 1, 1, 2])--卷积核（1，-1）；([1, 1, 2, 1])--卷积核（1，-1）.T；([1, 1, 2, 2])--卷积核（（1，-1），（-1，1））。画出原图pic，设为四维：x = pic.reshape([1, 1, 9, 9]) x = torch.Tensor(x)。以卷积核（1，-1）为例，创建卷积层conv1 = torch.nn.Conv2d(1, 1, [1, 2])。然后卷积：y1 = conv1(x).detach().numpy()再降维成n*n: plt.imshow(y1.squeeze(),cmap='Greys_r')
（三）
边缘检测中，我参照了学长的代码，觉得每次都要写一个完整的程序有点麻烦，想写一个def函数【使用指定的卷积核对图像进行卷积操作，同时将像素值控制（0，255）合理范围内】：
def kernel(kernel,im,conv1):
inout_kernel=kernel.reshape((1,1,3,3))
conv1.weight.data = torch.from_numpy(inout_kernel)
edge1 = conv1(im)
#确保图像数值不超过【0，255】
for i in range(edge1.shape[2]):
for j in range(edge1.shape[3]):
if edge1[0][0][i][j] > 255:
edge1[0][0][i][j] = 255
if edge1[0][0][i][j] < 0:
edge1[0][0][i][j] = 0
x = edge1.detach().numpy().squeeze()
return x但是，一运行，他说我的内核挂掉了：
不写成函数就没有这个问题。
在上边这个代码中，学长也解决了灰色问题：
就是
for i in range(edge1.shape[2]):
for j in range(edge1.shape[3]):
if edge1[0][0][i][j] > 255:
edge1[0][0][i][j] = 255
if edge1[0][0][i][j] < 0:
edge1[0][0][i][j] = 0（四）
还是有个小问题，我不知道为啥我用numpy写的，转置以后的图像都是全黑图。
（五）
学习就是一个探索的过程，感觉真的在求知：
我开始直接用numpy和卷积原理实现的卷积----
感觉卷积核多每次都写一个完整程序麻烦----
相同步骤部分改成def函数----
看到学长的，使用的pytorch，建立tensor卷积核和对应卷积层----我改
我自己想写一个def函数会简单一点，结果内核挂掉----我改
又返回最开始的学长的代码----
美女舍友写的遇到了灰色问题---【[23-24 秋学期]NNDL 作业6 卷积 [HBU]-CSDN博客】
我没遇到，后来又着重研究了学长的代码----
发现他的代码里灰色问题的解决方法----
最终我完成了我的作业