第二课.PyTorch入门
什么是PyTorch
Pytorch是一个基于Python的科学计算库,类似于Numpy,但可以使用GPU,可灵活开展深度学习实验,其数据结构tensor类似于ndarray,但tensor可以在GPU上加速运算
GPU版本Pytorch安装
GPU版本Pytorch的快速下载安装(比如cudatoolkit=10.0版本):
conda install cudatoolkit=10.0
conda install pytorch torchvision -c https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/pytorch
pytorch的导入为:
import torch
torch.__version__ #pytorch的版本号
Pytorch张量的基本操作
tensor的声明
#构造一个未初始化的5x3矩阵
torch.empty(5,3)
#构造一个随机初始化的5x3矩阵
torch.rand(5,3)#值在0到1
torch.randn(5,3)#标准正态分布,值在-1到1
#构造一个全零矩阵,数值类型为long(int64)
torch.zeros(5,3,dtype=torch.long)
#或者简写为
torch.zeros(5,3).long()
#直接从数据构建tensor
torch.tensor([1.0,2.0])
tensor的复刻
从一个已有的tensor构建新tensor,这样做的意义在于重用原来tensor的特征,例如数据类型,如果要更改数据类型,也可以通过关键字参数指定
#数据类型的复刻
x=torch.tensor([6,6],dtype=torch.double)
x_new=x.new_zeros(5,3) #数据类型也是float64
x_new=x.new_ones(5,3,dtype=torch.float) #数据类型改为float32
#tensor形状的复刻
x=torch.randn(6,6,dtype=torch.float)
x_new=torch.ones_like(x,dtype=torch.int32) #_like代表新tensor形状相同
#查看形状
x_new.shape
#等价于
x_new.size()
tensor的运算
tensor的运算方式很多,但无非基于加减乘除,卷积,矩阵等基本操作,下面将以加法操作为例子
x=torch.rand([5,3])
y=torch.rand([5,3])
#加法
x+y
#等价于
torch.add(x,y)
实际上,写x+y时,会自动调用方法torch.add();
in-place操作
另一种加法操作基于in-place,in-place看似不起眼,但是不注意使用会导致各种各样的漏洞
in-place的实际案例:
#in-place案例
# 用 id() 这个函数,其返回值是对象的内存地址
# 情景 1
a = torch.tensor([3.0, 1.0])
print(id(a)) # 2112716404344
a = a.exp()
print(id(a)) # 2112715008904
#在这个过程中a.exp()生成了一个新的对象,然后再让a指向它的地址,所以这不是个 inplace 操作
# 情景 2
a = torch.tensor([3.0, 1.0])
print(id(a)) # 2112716403840
a[0] = 10
print(id(a), a) # 2112716403840 tensor([10., 1.])
# inplace 操作,内存地址没变
in-place加法:
x=torch.rand([5,3])
y=torch.rand([5,3])
#in-place加法,为了节省空间,结果保存在原有对象中
print(y)
#in-place操作都有一个下划线结尾,一旦使用in-place,原对象必然会被改变
y.add_(x)
print(y)#加法结果保存在y内
###########################################
# i += 1 与 i = i+1 的区别
'''
对于Python数值对象,不存在in-place
'''
i = 0
print(id(i)) # 1564271360
i += 1
print(id(i)) # 1564271376
i = i + 1
print(id(i)) # 1564271392
'''
对于ndarray或是tensor,i+=1属于inplace,i=i+1不属于inplace
'''
import numpy as np
arr=np.array(6)
print(id(arr))
arr+=1
print(id(arr))
arr=arr+1
print(id(arr))
"""
140163988691504
140163988691504
140163988636272
"""
tensor索引和变形
Pytorch的索引与Numpy一致,切片也是左闭右开(Python魔法方法__getitem__中定义的规则)
print(x)
print(x[:,1:]) #取所有行,取第一列到最后一列
"""
tensor([[0.6817, 0.5885, 0.4934],
[0.4521, 0.7160, 0.6664],
[0.4955, 0.6965, 0.0801],
[0.5151, 0.2415, 0.4981],
[0.2836, 0.0920, 0.2456]])
tensor([[0.5885, 0.4934],
[0.7160, 0.6664],
[0.6965, 0.0801],
[0.2415, 0.4981],
[0.0920, 0.2456]])
"""
Resizing或者Reshape,在pytorch中是view
x=torch.randn(4,4)
print(x.shape)
y=x.view(16)
print(y.shape)
#指定某个维度为-1,则该维度会自动被计算出形状
z=x.view(2,-1)
print(z.shape)
"""
torch.Size([4, 4])
torch.Size([16])
torch.Size([2, 8])
"""
如果tensor内部只有一个元素,使用item()可以将value取出作为Python的数值
x[1,1]
#>tensor(0.1198)
x[1,1].item()
#>0.11984860897064209
补充:如果dir(tensor对象),得到张量内有两个重要对象:data和grad;
data是张量本身,gard是张量的梯度:
x=torch.randn(1)
x.data
x.grad
交换维度
tensor.transpose(dim0,dim1)交换维度0和维度1,所以,对于一个张量x(x是3维及以上的张量),x.transpose(0,2)等价于x.transpose(2,0)
x=torch.randn(5,3,2)
print(x.shape)
x_t=x.transpose(0,2)
print(x_t.shape)
"""
torch.Size([5, 3, 2])
torch.Size([2, 3, 5])
"""
ndarray和tensor类型转换
tensor默认在CPU上,在程序运行中,tensor将和ndarray共享内存,因此,CPU上的TorchTensor与NumpyNdarray之间的转换很容易
tensor转ndarray:
a=torch.ones(5)#tensor([1., 1., 1., 1., 1.])
#转为array
b=a.numpy()#array([1., 1., 1., 1., 1.], dtype=float32)
#共享内存
b[1]=6
print(a)#tensor([1., 6., 1., 1., 1.])
ndarray转tensor:
import numpy as np
import torch
a=np.ones(5)
b=torch.from_numpy(a)#生成tensor,赋值到b,b和a共享内存
#in-place操作
np.add(a,1,out=a)
"""
如果写a=a+1
b将还是tensor([1., 1., 1., 1., 1.]),如果写a=a+1,out并没有保存到原本的a对象,实际上是重新定义了对象,只是名字还叫a
"""
print(b)
#tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
#对a操作,改变了b,再次验证array与CPU的tensor共享内存
CUDA tensor
所谓CUDA tensor是指布置在GPU上的张量,GPU可以加速张量的计算,首先判断GPU是否可以使用:
#判断GPU是否可用
torch.cuda.is_available()
tensor默认在CPU上,现在将tensor迁移到GPU:
#把tensor布置到GPU上(tensor默认都是在CPU上)
x=torch.randn(5,3)
if torch.cuda.is_available():
device_gpu = torch.device("cuda")
y = torch.ones_like(x, device=device_gpu)
# 也可以直接用.to部署到gpu
x = x.to(device_gpu)
# z将在GPU上完成运算,对于小数据没有感觉到不同,对于大数据,会感受到明显的计算速度差异
z = x + y
print(z)
# 如果要将tensor转为array,必须先从GPU搬运到CPU
# 现在把z转回CPU
device_cpu = torch.device("cpu")
z = z.to(device=device_cpu, dtype=torch.double)
print(z)
z = z.numpy()
print(z)
Pytorch的tensor布置到GPU需要一步一步完成,为了化简步骤,可以先定义模型,然后直接:
molde=model.cuda(),自动将模型布置到GPU上;
对于设置某个张量的迁移,一般推荐使用.to()方法,可以具体选择要哪一个GPU
实验一:用Numpy实现两层神经网络
要求:全连接网络,激活函数为ReLU,权重不加bias,L2 loss,完全用Numpy实现前向和反向计算;
- h = W 1 X h=W_1X h=W1X
- a = m a x ( 0 , h ) a=max(0,h) a=max(0,h)
- y h a t = W 2 a y_{hat}=W_2a yhat=W2a
计算流程:
- forward pass
- loss
- backward pass
ndarray只是一个普通的n维array,它内部没有任何DL相关的对象(比如梯度),也不知道计算图,ndarray只是一个用于数学计算的数据结构
首先,熟悉numpy的一些操作,在np.后的方法,操作对象为每一个元素(可广播),比如:
np.maximum(y,0),y是一个6x3矩阵,maximum会将0广播到每个元素,返回比较结果,返回的依然是6x3矩阵;
np.square(y_pred-y)会取对应位置的每个元素求square,最后返回的结果还是6x3矩阵:
# 关于Numpy的操作
# 在np.后的方法,操作对象为每一个元素(可广播)
import numpy as np
y=np.random.randn(6,3)
y_pred=np.random.randn(6,3)
print(y)
print(np.maximum(y,0))
temp=np.square(y_pred-y)
temp.sum(),temp.mean()
"""
[[ 0.46866875 1.53064624 0.61860204]
[-1.81656938 -1.01940481 0.79725882]
[-1.03559533 0.78828324 1.17177584]
[ 2.10932798 0.08326097 -0.34045735]
[ 1.97852545 -0.4410186 0.4620433 ]
[-0.39703326 -1.46239008 0.35678806]]
[[0.46866875 1.53064624 0.61860204]
[0. 0. 0.79725882]
[0. 0.78828324 1.17177584]
[2.10932798 0.08326097 0. ]
[1.97852545 0. 0.4620433 ]
[0. 0. 0.35678806]]
(67.80287390030654, 3.7668263277948077)
"""
假设这个神经网络输入为1000,中间层输出为100,最后输出结果是10维,训练的样本为64,学习率设置1e-6:
import numpy as np
N=64 #样本数
D_in=1000
H=100 #中间层输出
D_out=10 #最后一层输出
# 随机创建训练数据
x=np.random.randn(N,D_in)
y=np.random.randn(N,D_out)
# 随机初始权重
w1=np.random.randn(D_in,H)
w2=np.random.randn(H,D_out)
learning_rate=1e-6
一共迭代500次(由于每次都是使用整个数据集更新,所以一次就是一个epoch),每次都需要前向传播,计算loss,反向传播梯度,更新权重:
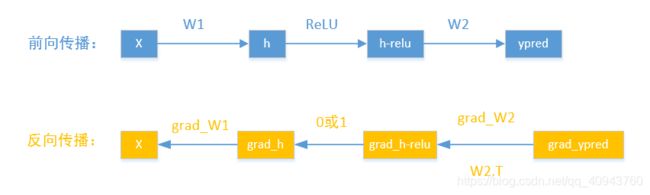
对于前向传播,按照要求为:
#Forward Pass
h=x.dot(w1) # x乘w1->N*H
h_relu=np.maximum(h,0) #N*H
y_pred=h_relu.dot(w2) # h_relu乘w2->N*D_out
然后计算loss:
#compute loss,假设用 MSE loss
loss=np.square(y_pred-y).sum()
#np.square(y_pred-y)为N*D_out,通过sum()对ndarray求和获得loss值(是一个数值)
然后反向传播梯度,目标是更新权重,所以最终需要的是权重的梯度:grad_w1,grad_w2;
求权重的梯度有公式:
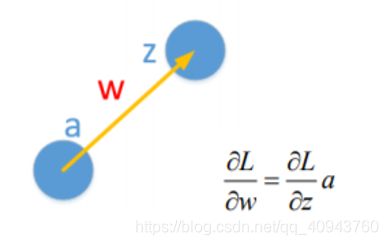
可以看出,要想知道权重的梯度必须知道前向计算时的激活值a,和反向传播时的下一神经元的激活前的z的梯度,求z的梯度才是体现反向传播的关键,比如本实验的grad_h_relu的计算:
g r a d _ h _ r e l u = g r a d _ y _ p r e d . d o t ( W 2 . T ) grad\_h\_relu=grad\_y\_pred.dot(W_2.T) grad_h_relu=grad_y_pred.dot(W2.T)
W 2 . T W_2.T W2.T是 W 2 W_2 W2的转置;
除此之外,梯度流经激活函数ReLU时,需要乘0或者1(相乘操作来自求导链式法则),即正向计算中,h大于0,相乘的导数是1,否则为0,可以大致写一个流程:
grad_h[h<0]=0;
grad_h[h>=0]=1*grad_h_relu;
但是实际实现时不要直接赋值,因为数组直接赋值,两者共享内存,最好进行深拷贝以避免不必要的错误;
于是这个网络的反向传播为:
#Backward Pass
#compute gradient
grad_y_pred=2.0*(y_pred-y)
grad_w2=h_relu.T.dot(grad_y_pred)
grad_h_relu=grad_y_pred.dot(w2.T) #N*D_out乘D_out*H->N*H
#深拷贝:拷贝到父子对象级别,前后完全是两个不相关的对象,以避免科学计算出现错误
grad_h=grad_h_relu.copy()
#Numpy的快速数据检索
grad_h[h<0]=0
grad_w1=x.T.dot(grad_h) #D_in*N乘N*H->D_in*H
最后更新权重:
#update weights of w1 and w2
w1=w1-learning_rate*grad_w1
w2=w2-learning_rate*grad_w2
完整的过程如下:
import numpy as np
N=64 #样本数
D_in=1000
H=100 #中间层输出
D_out=10 #最后一层输出
# 随机创建训练数据
x=np.random.randn(N,D_in)
y=np.random.randn(N,D_out)
# 随机初始权重
w1=np.random.randn(D_in,H)
w2=np.random.randn(H,D_out)
learning_rate=1e-6
for ite in range(500):
#Forward Pass
h=x.dot(w1) # x乘w1->N*H
h_relu=np.maximum(h,0) #N*H
y_pred=h_relu.dot(w2) # h_relu乘w2->N*D_out
#compute loss,假设用 MSE loss
loss=np.square(y_pred-y).sum() #np.square(y_pred-y)为N*D_out,通过sum()对ndarray求和获得loss值(是一个数值)
print(ite,loss)
#Backward Pass
#compute gradient
grad_y_pred=2.0*(y_pred-y)
grad_w2=h_relu.T.dot(grad_y_pred)
grad_h_relu=grad_y_pred.dot(w2.T) #N*D_out乘D_out*H->N*H
#深拷贝:拷贝到父子对象级别,前后完全是两个不相关的对象,以避免科学计算出现错误
grad_h=grad_h_relu.copy()
#Numpy的快速数据检索
grad_h[h<0]=0
grad_w1=x.T.dot(grad_h) #D_in*N乘N*H->D_in*H
#update weights of w1 and w2
w1=w1-learning_rate*grad_w1
w2=w2-learning_rate*grad_w2
使用numpy实现神经网络有助于充分了解forward pass和backward pass的整个过程
实验二:用Pytorch完成实验一
数据从ndarray更换到tensor;
矩阵乘法在np中是.dot,在pytorch中是.mm(即matrix multiplication);
torch的clamp()比numpy的maximum()更好,clamp类似钳位电路,可设置min钳位和max钳位,让在值内的信号通过,否则为min,max;
因此,获得第一次的修改:
import torch
N=64 #样本数
D_in=1000
H=100 #中间层输出
D_out=10 #最后一层输出
# 随机创建训练数据
x=torch.randn(N,D_in)
y=torch.randn(N,D_out)
# 随机初始权重
w1=torch.randn(D_in,H)
w2=torch.randn(H,D_out)
learning_rate=1e-6
for ite in range(500):
#Forward Pass
h=x.mm(w1) # x乘w1->N*H
h_relu=h.clamp(min=0) #N*H
y_pred=h_relu.mm(w2) # h_relu乘w2->N*D_out
#compute loss,假设用 MSE loss
loss=(y_pred-y).pow(2).sum().item() #sum结果是tensor,所以用item()转为Python数值
print(ite,loss)
#Backward Pass
#pytorch是会自动求梯度的,但强行手动反向传播也不是不行
grad_y_pred=2.0*(y_pred-y)
grad_w2=h_relu.t().mm(grad_y_pred)
grad_h_relu=grad_y_pred.mm(w2.t()) #N*D_out乘D_out*H->N*H
#深拷贝:拷贝到父子对象级别,前后完全是两个不相关的对象,以避免科学计算出现错误
grad_h=grad_h_relu.clone()
#快速数据检索
grad_h[h<0]=0
grad_w1=x.t().mm(grad_h) #D_in*N乘N*H->D_in*H
#update weights of w1 and w2
w1=w1-learning_rate*grad_w1
w2=w2-learning_rate*grad_w2
以上修改中,我还是人为地去计算梯度了,pytorch支持自动求梯度(依据定义模型的计算图),所以先探索一下autograd,当定义一个张量时,有参数requires_grad默认为False,该参数用于前向传播时自动计算梯度:
#pytorch的autograd(自动求梯度)
x=torch.tensor(6,requires_grad=True,dtype=torch.float32)
对于自动计算梯度的认识,有以下简单实例:
#简单的自动求梯度
x=torch.tensor(1.) #x不能自动计算梯度
w=torch.tensor(2.,requires_grad=True)
b=torch.tensor(3.,requires_grad=True)
#这是一个计算图
y=w*x+b #y=2*1+3
#反向计算不用手动写过程(基于计算图自动反向计算),直接写:
y.backward()
#dy/dw
print(w.grad)
#dy/dx,由于x的requires_grad=False,所以其梯度为None
print(x.grad)
#dy/db
print(b.grad)
"""
tensor(1.)
None
tensor(1.)
"""
这里补充一下,这样的实例看起来很正常,但当我在训练中inplace更新权重时,将会遇到一些错误,所以先了解一下叶子张量
叶子张量
叶子张量(叶子节点)是人为定义的张量,为了节省显存,运算完一次,非叶子节点(由节点生成的节点,因为它类似于临时变量)的梯度就会被释放,当然,可以用tensor.retain_grad()保存非叶子节点的梯度;
如果只是为了打印梯度而便于调试,可以用tensor.register_hook();
注意,不管requires_grad是True还是False,人为定义的tensor都是叶子节点:

看完叶子张量,再了解一下torch.no_grad()
torch.no_grad()
当我们在做 evaluating 的时候(不需要计算导数),我们可以将推断(inference)的代码包裹在 with torch.no_grad() 之中,以达到暂时不追踪网络参数中的导数的目的;
如果用pytorch的autograd(比如之前的w1.grad)去更新参数,写成in-place的形式才能更新,为什么?
因为一旦写成:
w1=w1-learning_rate*w1.grad
就代表w1已经不再是叶子节点,loss.backward()语句结束后,w1的梯度就被间隔性释放了,更新时有可能出现根本找不到w1.grad(已经为None)的情况;
而pytorch又有规定,对于requires_grad为True的张量,不允许in-place更新,现在很矛盾,那该如何更新?
1.首先可以用torch.no_grad(),将更新语句置于其下,这样,执行到torch.no_grad(),pytorch不会检查(追踪)张量的requires_grad,此时就可以放心进行in-place,但注意一点,w.grad的结果是不断累积的,为了避免训练出错,必须在每次更新前进行grad对象清零:
w1.grad.zero_()
上述过程为:
with torch.no_grad():
#in-place更新时,需要指定暂时不追踪计算图,不然没法更新
#如果不用in-place更新,w=w-grad*lr,会导致叶子节点w变成非叶子节点,梯度会丢失,从而无法更新
w1-=learning_rate*w1.grad
w2-=learning_rate*w2.grad
#梯度会累加,需要每次进行清零
w1.grad.zero_()
w2.grad.zero_()
2.另一种方式下,依然追踪计算图,当然就不能in-place了,但是我可以在loss.backward()前保留梯度:
w1.retain_grad()
w2.retain_grad()
#Backward Pass
loss.backward()
w1=w1-learning_rate*w1.grad
w2=w2-learning_rate*w2.grad
现在,通过自动梯度,简化实验如下:
#借助autograd化简代码
import torch
N=64 #样本数
D_in=1000
H=100 #中间层输出
D_out=10 #最后一层输出
# 随机创建训练数据
x=torch.randn(N,D_in)
y=torch.randn(N,D_out)
# 随机初始权重
w1=torch.randn(D_in,H,requires_grad=True)
w2=torch.randn(H,D_out,requires_grad=True)
learning_rate=1e-6
for ite in range(500):
#Forward Pass
h=x.mm(w1) # x乘w1->N*H
h_relu=h.clamp(min=0) #N*H
y_pred=h_relu.mm(w2) # h_relu乘w2->N*D_out
#compute loss,假设用 MSE loss
loss=(y_pred-y).pow(2).sum() # 基于pytorch的实现,loss(不进行item)实际是computation graph
loss_value=loss.item()
print(ite,loss_value)
#Backward Pass
loss.backward()
with torch.no_grad():
#in-place更新时,需要指定暂时不追踪计算图,不然没法更新
#如果不用in-place更新,w=w-grad*lr,会导致叶子节点w变成非叶子节点,梯度会丢失,从而无法更新
w1-=learning_rate*w1.grad
w2-=learning_rate*w2.grad
#梯度会累加,需要每次进行清零
w1.grad.zero_()
w2.grad.zero_()
进一步化简
上面这样写总感觉还有些麻烦;
pytorch还有一个库nn,使用起来就像keras一样搭建积木,可以用网络库nn化简:
#Pytorch内部提供了一个丰富的网络库:nn
#使用起来就像keras
import torch.nn
N,D_in,H,D_out=64,1000,100,10
#随机生成训练数据
x=torch.randn(N,D_in)
y=torch.randn(N,D_out)
#使用Sequential搭建模型
model=torch.nn.Sequential(
torch.nn.Linear(D_in,H),#默认bias=True
torch.nn.ReLU(),
torch.nn.Linear(H,D_out)
)
#设置模型初始化
torch.nn.init.normal_(model[0].weight)
#model[1]是ReLU,没法初始化权重
torch.nn.init.normal_(model[2].weight)
if torch.cuda.is_available():
model=model.cuda()
#reduction决定了输出张量维度缩减的方式,默认是mean
loss_fn=torch.nn.MSELoss(reduction='sum')
learning_rate=1e-6
for ite in range(500):
#前向传播
y_pred=model(x)#本质是call :model.forward(x)
#计算loss
loss=loss_fn(y_pred,y)
print(ite,loss.item())
#反向传播
loss.backward()
with torch.no_grad():
#model.parameters()是模型的参数集合
for param in model.parameters():
param-=learning_rate*param.grad
#参数梯度清零,直接简写为
model.zero_grad()
还可以查看model[0]的权重,第0层:
torch.nn.Linear(D_in,H)

使用优化器训练
训练不必须使用传统的梯度下降,还可以选择Adam等更高阶的优化方法:
#优化方法
import torch.nn
import torch
N,D_in,H,D_out=64,1000,100,10
#随机生成训练数据
x=torch.randn(N,D_in)
y=torch.randn(N,D_out)
#使用Sequential搭建模型
model=torch.nn.Sequential(
torch.nn.Linear(D_in,H),#默认bias=True
torch.nn.ReLU(),
torch.nn.Linear(H,D_out)
)
#这里没有正态分布初始化,初始化与optimizer有联系,Adam不一定适合正态分布初始化
if torch.cuda.is_available():
model=model.cuda()
#reduction决定了输出张量维度缩减的方式,默认是mean
loss_fn=torch.nn.MSELoss(reduction='sum')
learning_rate=1e-4 #Adam一般使用1e-3到1e-4
#优化方法,不再使用传统的梯度更新
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)
for ite in range(500):
#前向传播
y_pred=model(x)
#计算loss
loss=loss_fn(y_pred,y)
print(ite,loss.item())
#反向传播
loss.backward()
#更新模型
optimizer.step()
#梯度清零
optimizer.zero_grad()
基于优化器,代码更加简洁:
loss.backward()用于计算好梯度;
optimizer.step()根据计算好的梯度进行更新;
optimizer.zero_grad()用于在下一次梯度计算前进行梯度清零,等价于model.zero_grad()
模型定义进阶
上次模型定义依赖于torch.nn.Sequential,我现在继承一个子类,用自定义的类去初始化模型;
一般来说,只要在__init__()和forward()两个方法进行修改就能满足部分需求;
模型继承自torch.nn.Module,要遵循规则:
1.要求导的层需要定义在__init__下
2.层的前向传播过程写在forward下
class TowLayerNet(torch.nn.Module):
def __init__(self,D_in,H,D_out):
#子类调用父类初始化,继承到父类的所有属性
super().__init__()
self.linear1=torch.nn.Linear(D_in,H,bias=False)
self.linear2=torch.nn.Linear(H,D_out,bias=False)
def forward(self,x):
y_pred=self.linear2(self.linear1(x).clamp(min=0))
return y_pred
实例化网络:
model=TowLayerNet(D_in,H,D_out)
前向传播:
y_pred=model.forward(x)
#或者
y_pred=model(x)
完整实现:
#模型定义进阶
import torch.nn
import torch
N,D_in,H,D_out=64,1000,100,10
#随机生成训练数据
x=torch.randn(N,D_in)
y=torch.randn(N,D_out)
#模型继承自torch.nn.Module,要遵循规则:要求导的层需要定义在__init__下
#层的前向传播过程写在forward下
class TowLayerNet(torch.nn.Module):
def __init__(self,D_in,H,D_out):
#子类调用父类初始化,继承到父类的所有属性
super().__init__()
self.linear1=torch.nn.Linear(D_in,H,bias=False)
self.linear2=torch.nn.Linear(H,D_out,bias=False)
def forward(self,x):
y_pred=self.linear2(self.linear1(x).clamp(min=0))
return y_pred
model=TowLayerNet(D_in,H,D_out)
if torch.cuda.is_available():
model=model.cuda()
#reduction决定了输出张量维度缩减的方式,默认是mean
loss_fn=torch.nn.MSELoss(reduction='sum')
learning_rate=1e-4 #Adam一般使用1e-3到1e-4
#优化方法,不再使用传统的梯度更新
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)
for ite in range(500):
#前向传播
y_pred=model(x)
#计算loss
loss=loss_fn(y_pred,y)
print(ite,loss.item())
#反向传播
loss.backward()
#更新模型
optimizer.step()
#梯度清零
optimizer.zero_grad()