java TreeSet,TreeMap——红黑树原理
在java中使用TreeSet集合时,需要对加入的元素进行比较,对于同一个类的元素之间进行比较,需要实现Comparable接口的compareTo(Object obj)方法,对于不同类之间的元素比较,需要实现Comparator接口的compare(Object obj1,Object obj2)方法
加入元素的add(Object obj)方法的内部:
public boolean add(E e) {
return m.put(e, PRESENT)==null;
}
m是Map的一个类型,这里的put方法是TreeMap里put的实现:
public V put(K key, V value) {
Entry t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry parent;
// split comparator and comparable paths
Comparator cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
可能要进入正题了,从put的第一行就可以看出来TreeMap果然用的是tree,一点点解读它
Entry t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
首先将自己定义的root给了Entry
接下来就是关于元素之间的比较了:
int cmp;
Entry parent;
// split comparator and comparable paths
Comparator cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
这里面的cpr != null代表了该元素类或者它的超类实现了Comparator接口,就开始了和它父节点开始比较,使用的是实现的compare(Object obj1,Object obj2)方法比较,可以看到,如果返回值小于0,它将成为父亲的左孩子,如果大于0,将成为父亲的右孩子。这和下面的实现Comparable接口的十分相似:
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
两种情况都使用了while循环以遍历到没有子节点的叶子节点,这其实涉及到的是二叉查找数(也叫二叉排序树):
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树
举个例子:

简单来说就是每个节点的左孩子比他小,右孩子比他大,这样在查询上会快很多,但是总会有特殊情况发生,比如这样的:

天,这样一直右孩子到底还不如不要什么二叉查找树了,所以针对这种情况,我们的TerrMap引入红黑树来解决问题
就是put最后这段代码:
Entry e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
e就是这最后一个叶子节点嘛,智商超高的我们一眼看出了关键——fixAfterInsertion(e);
看看实现:
private void fixAfterInsertion(Entry x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { //1.
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) { //2.
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK); //3.
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { //4.
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) { //5.
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK); //6.
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
乍一看这代码有点蒙圈,所以事先了解一下什么是红黑树(平衡二叉树的一种实现)很必要。
首先红黑树本身就是二叉查找树,并且具有以下的性质:
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
并且在红黑树中,空节点是黑色
好,现在跟着代码来看看它究竟是如何做到上述的性质的,并且看看这样有什么意义;
首先:x.color = RED;
这个x代表的含义就是我们插入的节点,它现在因为put中的遍历已经成为了叶子节点,那这个意思就是把它的颜色改成红的呗。
接下来就是while (x != null && x != root && x.parent.color == RED)
我们的所有处理代码全在这个里面,看来红黑树发动的条件是插入的节点的父节点是红色
在代码最后root.color = BLACK;将根节点转变为黑色,意思就是如果只有书上只有一个节点,它将是作为跟节点并且是黑色的,插入的节点是红色的,给个图更清晰:

分析代码可以看到处理情况分为下面几种:
1.父亲节点是祖父节点的左孩子,叔叔节点是红色,
2.父亲节点是祖父节点的左孩子,叔叔节点是黑色,该节点是右孩子
3.父亲节点是祖父节点的左孩子,叔叔节点是黑色,该节点是左孩子
4.父亲节点是祖父节点的右孩子,叔叔节点是红色
5.父亲节点是祖父节点的右孩子,叔叔节点是黑色,该节点是左孩子
6.父亲节点是祖父节点的右孩子,叔叔节点是黑色,该节点是右孩子
3个以上的节点就会开始处理了
例如加入25会时最开始会出现下图(注意空节点是黑色)
在上述程序标出
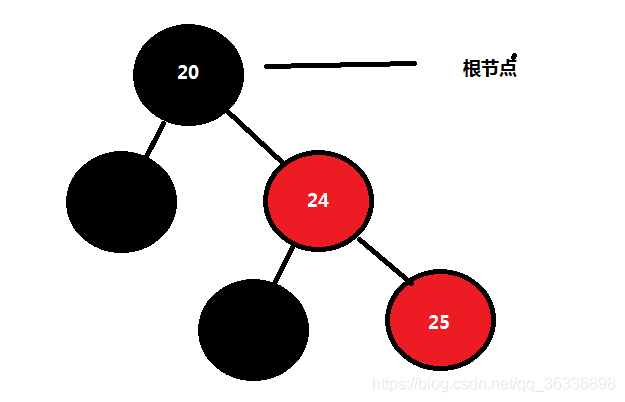
红色节点的父节点是红色时,需要处理,这里可以看到插入节点25的 父节点是祖父节点的右孩子,叔叔节点是黑色,该节点是右孩子,对应情况6,对应代码是:
setColor(parentOf(x), BLACK); //6.
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
可以看到,这里将父节点设置成黑色,祖父节点设置为红色,然后来了个rotateLeft(parentOf(parentOf(x)));
这就是红黑树里面树的左旋转,先简单画一下什么是左旋转:
如下是以a为轴的左旋
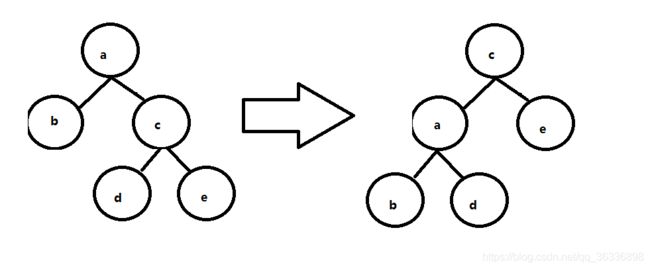
它当然有对应的代码:
private void rotateLeft(Entry p) {
if (p != null) {
Entry r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
当然对应的也有右旋转,以a为轴右旋

所以改变颜色加旋转后

树的深度降低了!
再插入30试试:

父亲节点是祖父节点的右孩子,叔叔节点是红色,对应情况4,代码:
if (colorOf(y) == RED) { //4.
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
将父节点和叔叔节点都设置成黑色了,这确实是很简便的方法,x会成为它自己的祖父节点继续做处理。

为了了解他多插入几个数:40

父亲节点是祖父节点的右孩子,叔叔节点是黑色,该节点是右孩子,情况6(以下不一一写处理代码,详情请见上)

接着插入10:

父节点是黑色的,无需处理
插入8:
父亲节点是祖父节点的左孩子,叔叔节点是黑色,该节点是左孩子,情况3:

这里用到了右旋转。示意如下
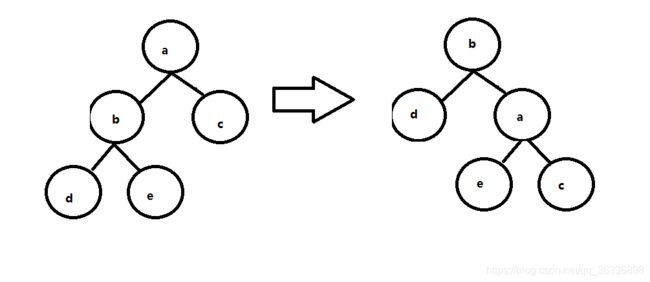
好了不在一一插入了,我们可以根据代码最后概况每种情况并寻找这样做的意图
1.父亲节点是祖父节点的左孩子,叔叔节点是红色
父节点变黑,叔叔节点变黑,祖父节点变红
2.父亲节点是祖父节点的左孩子,叔叔节点是黑色,该节点是右孩子
将x先变为他的父节点,再以x为轴左旋转,该节点会成为左孩子节点,这时就会变成情况3
3.父亲节点是祖父节点的左孩子,叔叔节点是黑色,该节点是左孩子
将父亲节点变黑色,祖父节点变为红色,以祖父节点为轴右旋转
4.父亲节点是祖父节点的右孩子,叔叔节点是红色
父节点变黑,叔叔节点变黑,祖父节点变红
5.父亲节点是祖父节点的右孩子,叔叔节点是黑色,该节点是左孩子
将x先变为他的父节点,再以x为轴右旋转,该节点会成为右孩子节点,这时就会变成情况6
6.父亲节点是祖父节点的右孩子,叔叔节点是黑色,该节点是右孩子
将父亲节点变黑色,祖父节点变为红色,以祖父节点为轴左旋转
这六种情况都试图将树的每层统一为同一种颜色,这样保证性质4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
通过改变颜色保证性质3 每个红色节点的两个子节点都是黑色。
同时通过树的旋转来保证树的深度不过大。