机器学习之用逻辑回归制作评分卡（分类分析：基于UCI的german信用评分卡设计）

---

前言

提示：这里可以添加本文要记录的大概内容：
本次实验希望通过利用来自UCI数据集中的german.data进行数据处理和特征选择。之后通过逻辑回归进行模型构建与评估，然后构建评分卡模型，分数转化生成评分卡，最后制作符合业务要求且兼顾用户体验的评分卡。

---

提示：工具选择：JupyterLab notebook

一、知识准备

1.构建逻辑回归模型


Sigmoid函数





逻辑回归（Logistic Regression）是对数几率回归，属于广义线性模型（GLM），它的因变量一般只有0或1.
线性回归并没有对数据的分布进行任何假设，而逻辑回归隐含了一个基本假设 ：每个样本均独立服从于伯努利分布（0-1分布）

2.分箱
分箱方法：等频分箱、等距分箱（pandas的cut和qcut函数）、Chi-megerd卡方分箱，Best-KS方法（局限性较多，不建议使用），IV最优分箱，基于树的最优分箱（信息增益，gini指数等）。
3.特征选择

4.评分卡构建
关于评分卡的构建的理论知识，读者可仔细阅读以下文章：
1.信用评分卡模型的理论准备
2.让你彻底理解信用评分卡原理（Python实现评分卡代码）

二、数据获取及读入

1. 数据准备：来自UCI数据集https://archive.ics.uci.edu/ml/machine-learning-databases/statlog/german/
2. 读入数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] # SimHei.ttf
plt.rcParams['axes.unicode_minus'] = False 
rc = {'font.sans-serif': 'SimHei',
      'axes.unicode_minus': False}

data = pd.read_csv('数据/german.data',header = None ,sep='\\s+')
# display(df.head(2))
#变量重命名
#account_status（（定性）现有支票帐户的状况）；period（（数值）月份持续时间，还了多久的贷款了）；history_credit（（定性）信用记录）
#credit_purpose（（定性）贷款目的）；credit_limit（（数值）信用额）；saving_account（（定性）储蓄账户/债券）
#person_employee（（定性）目前就业（就业年限））；income_installment_rate（（数值）分期付款率按可支配收入的百分比计算）；marry_sex（（定性）个人地位和性别）
#other_debtor（（定性）其他债务人/担保人）；address（（数值）现在居住地）；property（（定性）属性）
#age（数值）年龄；installment_plans（（定性）其他分期付款计划）；housing（（定性）住房）
#credits_num（（数值）此银行现有的信用额）；job（（定性）工作）；dependents（（数值）可还款人数）
#have_phone（（定性）电话）；foreign_worker（（定性）外国工人）；target（ 信用好坏）

columns = ["account_status","period","history_credit","credit_purpose","credit_limit","saving_account","person_employee",
           "income_installment_rate","marry_sex","other_debtor","address","property","age","installment_plans","housing","credits_num","job","dependents","have_phone","foreign_worker","target"]
data.columns = columns
##将标签变量由状态1,2转为0,1;0表示好用户，1表示坏用户
data.target = data.target - 1
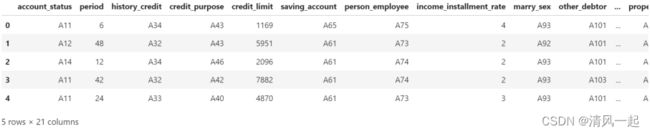
data.head()

三、数据处理

3.1.缺失值处理

#查看数据属性
data.info()

由上图可以看出，每一列并不存在缺失值，不需要进行缺失值处理。

3.2.异常值处理

#查看连续变量数据分布
data.describe()

由上图及结合各个列数据的含义及实际情况，认为各连续变量均分布在合理范围内。

3.3.重复值处理

#查看是否有重复值
data[data.duplicated()==True]
#异常值应该不存在，不做探究

四、探索性分析

#分辨出连续变量与离散变量 
feature_names = ["account_status","period","history_credit","credit_purpose","credit_limit","saving_account","person_employee",
           "income_installment_rate","marry_sex","other_debtor","address","property","age","installment_plans","housing","credits_num","job","dependents","have_phone","foreign_worker"]
#所有列名
categorical_var = [] #保存离散变量列名
numerical_var = []  #保存连续型变量列名
##先判断类型，如果是int或float就直接作为连续变量
numerical_var = list(data[feature_names].select_dtypes(include=['int','float','int32','float32','int64','float64']).columns.values)
categorical_var = [x for x in feature_names if x not in numerical_var]
display(categorical_var)
display(numerical_var)

4.1.查看数据分布是否平衡

#查看一下好坏客户分布
sns.set(style = 'darkgrid',color_codes = True,rc=rc)
sns.countplot(x = df['target'],data = df)

可知，数据并不平衡，需要进行样本平衡处理。

4.2.样本平衡

由上面结果，我们可以知道，存在样本不平衡问题，需要进行样本平衡，采用过采样（上采样）的方法。RandomOverSampler通过对少数类样本进行有放回地随机采样来生成少数类的样本。

#样本平衡
from imblearn.over_sampling import RandomOverSampler
ros = RandomOverSampler(random_state=42)
X,y= ros.fit_resample(X,y)

n_sample_ = X.shape[0]#278584

pd.Series(y).value_counts()
 
n_1_sample = pd.Series(y).value_counts()[1]
n_0_sample = pd.Series(y).value_counts()[0]
 
print('样本个数：{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))
#样本个数：278584; 1占50.00%; 0占50.00%

4.3.离散型变量在好坏客户上的分布

#离散型变量  在好客户与坏客户分布上的可视化
p = 1
plt.figure(figsize=(20,18))
row = 5  #画布为几行
col = 3  #画布为几列
for i in categorical_var[0:13]:
    # df_var = "df_" + i
    df_var = pd.crosstab(df[i],df["target"])
    df_var["bad_rate"] = round(df_var[1]/(df_var[1]+df_var[0]),4)
    # display(df_var)
    # print(df_var.index)
    # print(df_var.columns)
    # print(p)
    
    #添加子区间绘制，
    ax1 = plt.subplot(row,col,p) #子区空间为n行n列 

    year = df_var.index # 横坐标
    data1 = df_var[0] # 纵坐标 好用户
    data2 = df_var[1] # 纵坐标 坏用户
    data3 = df_var["bad_rate"]  #坏用户占比

    # 先得到year长度, 再得到下标组成列表
    x = range(len(year))
    bar_width = 0.3  #每一个柱子偏移的距离

    # 好坏用户柱状图
    ax1.bar(x, data1, width=bar_width, color='#3A669C', label="好用户")
    # 向右移动0.2, 柱状条宽度为0.2
    #坏用户柱状图
    ax1.bar([i + bar_width for i in x], data2, width=bar_width, color='#C0504D',label="违约用户")

    # 底部汉字移动到两个柱状条中间(本来汉字是在左边蓝色柱状条下面, 向右移动0.1)
    plt.xticks([i + bar_width/2 for i in x], year)
    if p == 1 or p == col+1:
        ax1.set_ylabel('用户数量',size=10)
    ax1.set_xlabel(i,size=10) #很坐标的标签设为列名

    text_heiht = 3
    # 为每个条形图添加数值标签
    for x1,y1 in enumerate(data1):
        ax1.text(x1, y1+text_heiht, y1,ha='center',fontsize=8)
    for x2,y2 in enumerate(data2):
        ax1.text(x2+bar_width,y2+text_heiht,y2,ha='center',fontsize=8)

    # bad_rate线 共用纵坐标轴
    ax2 = ax1.twinx()
    p3 = ax2.plot([i + bar_width/2 for i in x], data3, color="gray",linestyle='--', label="坏用户占比")

    if p == 3 or p == 6:
        ax2.set_ylabel("坏用户占比")
    showlabel=True
    if p == 1 and showlabel == True:
        ax1.legend(loc="upper center")
        ax2.legend(loc=2)

    p = p + 1

plt.show()

4.4.连续型变量在好坏客户上的分布

#连续性变量分布直方图
p = 1
plt.figure(figsize=(20,18))
row = 4  #画布为几行
col = 2  #画布为几列
for i in numerical_var[0:7]:
    df_var = "df_" + i
    df_var = pd.DataFrame({'target':df["target"],'variables':df[i]})
    
    df_var_good = df_var.loc[df_var["target"]==0,]
    df_var_good = df_var_good.sort_values(["variables"]) #排序

    df_var_bad = df_var.loc[df_var["target"]==1,]
    df_var_bad = df_var_bad.sort_values(["variables"]) #排序

    plt.subplot(row,col,p) #子区空间为2行3列 
    if i == "period" or i == "age":
        bins_i = 60
    elif i == "credit_limit":
        bins_i = 150
    else:
        bins_i = 50
    #参数density=True表示是否归一化
    plt.hist(df_var_good["variables"],bins=bins_i,color='r',alpha=0.5,rwidth=0.6,density=True,label='好用户') 
    plt.hist(df_var_bad['variables'],bins=bins_i,color='b',alpha=0.5,rwidth=0.6,density=True,label='坏用户')
    plt.legend()
    if p == 1:
        plt.title('好坏用户分布直方图')
    plt.xlabel(i)
    plt.ylabel('count')

    p = p+1

plt.show()

五、数据预处理

主要式分箱及WOE的转换

5.1.离散变量WOE值转换

woeall = {}  #定义保存各分类（分箱）weo值字典
woe1 = {}  
for i in categorical_var:
    element = list(df[i].unique())
    for j in element:
        all1 = len(df[df[i]==j])
        bad = len(df[(df[i]==j)&(df['target']==1)])
        good = len(df[(df[i]==j)&(df['target']==0)])
        woe = np.log((good/all1)/(bad/all1))
        woe1[j] = round(woe,3)
        df.loc[df[i]==j,i] = round(woe,3)
    woeall[i] = woe1
    woe1 = {}
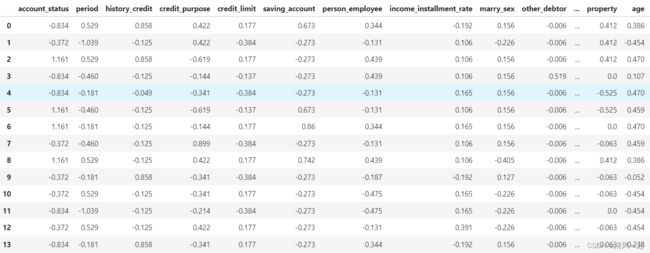
df.head(10)
#保存标签和weo值到字典中

woeall #查看以下各列各元素对应的WOE值

5.2.连续型变量的分箱及WOE值转换

1.定义预分箱函数（等距分箱）

# 在 统计学中, 以查尔斯·爱德华·斯皮尔曼命名的斯皮尔曼等级相关系数，即spearman相关系数。经常用希腊字母ρ表示。
# 它是衡量两个变量的依赖性的 非参数 指标。 它利用单调方程评价两个统计变量的相关性。 
# 如果数据中没有重复值， 并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1
#0表示好用户，1表示坏用户
# from scipy import stats
def mono_bin1(Y,X,n = 2):
    # r = 0
    bad = Y.sum()   #坏客户的个数
    good = Y.count()-bad  #好客户的个数
    list1 = []
    while n < 11:
        d1 = pd.DataFrame({"X":X,"Y":Y,"Bucket":pd.cut(X,n,duplicates='drop')})  ##将原数据离散化，分成20份区间
        d2 = d1.groupby('Bucket',as_index = True)    #以区间的分组
        # r,p = stats.spearmanr(d2.mean().X,d2.mean().Y)   #每一个区间的平均值与每一个区间分类的平均值
        n = n+1
        d3 = pd.DataFrame(d2.X.min(),columns = ['min'])   #该分区的最小值
        d3['min'] = d2.min().X
        d3['max'] = d2.max().X
        d3['sum'] = d2.sum().Y        #坏客户总数
        d3['total'] = d2.count().Y    #客户总数
        d3['rate'] = d2.mean().Y     #这个是坏的客户的占比
        d3['Distribution_Good'] = (d3['total'] - d3['sum']) / ((d3['total'] - d3['sum']).sum()) #相对于ppt中good%
        d3['Distribution_Bad'] = d3['sum'] / d3['sum'].sum() #相对于ppt中bad%
        d3['weo'] = np.log(d3['Distribution_Good'] / d3['Distribution_Bad'])
        iv = (d3['weo'] * (d3['Distribution_Good'] - d3['Distribution_Bad'])).sum()
        list1.append(iv)
    return list1

# 1.定义DataFrame,存放我们的每一个列的iv值
df_iv = pd.DataFrame()

#连续变量列
dd = ['period',
 'credit_limit',
 'income_installment_rate',
 'address',
 'age',
 'credits_num',
 'dependents']
for i in dd:
    df_iv[i] = mono_bin1(df['target'],df[i])

df_iv['份数'] =[2,3,4,5,6,7,8,9,10]
df_iv

# 1.定义DataFrame,存放我们的每一个列的iv值
df_iv = pd.DataFrame()

#连续变量列
dd = ['period',
 'credit_limit',
 'income_installment_rate',
 'address',
 'age',
 'credits_num',
 'dependents']
for i in dd:
    df_iv[i] = mono_bin1(df['target'],df[i])

df_iv['份数'] =[2,3,4,5,6,7,8,9,10]
df_iv

2.可视化df_iv，观察每一个变量最适合的分箱数

p = 1
plt.figure(figsize=(22,18))
row = 5  #画布为几行
col = 2  #画布为几列
for i in df_iv.iloc[:,0:7]:
    
    plt.subplot(row,col,p) #子区空间为2行3列 
    #参数density=True表示是否归一化
    plt.plot(df_iv['份数'], df_iv[i], marker ='*', linewidth=2, linestyle='--', color='orange')
    plt.title(i)
    # plt.hist(df_iv[i],color='r',alpha=0.5,rwidth=0.6,density=True) 
    p = p+1
plt.show()

3.正式分箱函数（等距分箱）

#0表示好用户，1表示坏用户
from scipy import stats
def mono_bin(Y,X,n):
    bad = Y.sum()   #坏客户的个数
    good = Y.count()-bad  #好客户的个数
    d1 = pd.DataFrame({"X":X,"Y":Y,"Bucket":pd.cut(X,n,duplicates='drop')})  ##将原数据离散化
    d2 = d1.groupby('Bucket',as_index = True)    #以区间的分组
    d5 = d1['Bucket'].sort_values().astype('str').unique()
    d3 = pd.DataFrame(d2.X.min(),columns = ['min'])   #该分区的最小值
    d3['min'] = d2.min().X
    d3['max'] = d2.max().X
    d3['sum'] = d2.sum().Y        #坏客户总数
    d3['total'] = d2.count().Y    #客户总数
    d3['rate'] = d2.mean().Y     #这个是坏的客户的占比
    d3['Distribution_Good'] = (d3['total'] - d3['sum']) / ((d3['total'] - d3['sum']).sum()) #相对于ppt中good%
    d3['Distribution_Bad'] = d3['sum'] / d3['sum'].sum() #相对于ppt中bad%
    d3['weo'] = np.log(d3['Distribution_Good'] / d3['Distribution_Bad'])
    iv = (d3['weo'] * (d3['Distribution_Good'] - d3['Distribution_Bad'])).sum()
    d4 = (d3.sort_values(by = 'min')).reset_index(drop = True)
    cut = []
    cut.append(float('-inf'))
    for i in range(len(d5)-1):
        x = eval(d5[i].split(',')[1][:-1])
        cut.append(x)
    cut.append(float('inf'))
    weo = list(d4['weo'].round(3))
    woe1={}
    for j in range(len(cut)-1):
        val = '('+str(cut[j])+','+str(cut[j+1])+']'
        woe1[val] = weo[j]
    woeall[X.name] = woe1
    woe1 = {}
    return d4,iv,cut,weo

d4_period,iv_period,cut_period,weo_period = mono_bin(df['target'],df['period'],5)
d4_credit_limit ,iv_credit_limit,cut_credit_limit,weo_credit_limit = mono_bin(df['target'],df['credit_limit'],5)
d4_income_installment_rate ,iv_income_installment_rate,cut_income_installment_rate,weo_income_installment_rate = mono_bin(df['target'],df['income_installment_rate'],4)
d4_address ,iv_address,cut_address,weo_address= mono_bin(df['target'],df['address'],4)
d4_age ,iv_age,cut_age,weo_age= mono_bin(df['target'],df['age'],8)
d4_credits_num ,iv_credits_num,cut_credits_num,weo_credits_num= mono_bin(df['target'],df['credits_num'],4)

4.连续变量WOE值转换函数

#连续变量WEO转换
def replace_weo(series,cut,weo):
    list1 = []
    i = 0
    while i<len(series):
        value = series[i]
        j = len(cut)-2
        m = len(cut)-2
        while j >=0:
            if value >=cut[j]:
                j = -1
            else:
                j = j-1
                m = m -1
        list1.append(weo[m])
        i = i+1
    return list1

df['period'] = pd.Series(replace_weo(df['period'],cut_period,weo_period))
df['credit_limit'] = pd.Series(replace_weo(df['credit_limit'],cut_credit_limit,weo_credit_limit))
df['income_installment_rate'] = pd.Series(replace_weo(df['income_installment_rate'],cut_income_installment_rate,weo_income_installment_rate))
df['address'] = pd.Series(replace_weo(df['address'],cut_address,weo_address))
df['age'] = pd.Series(replace_weo(df['age'],cut_age,weo_age))
df['credits_num'] = pd.Series(replace_weo(df['credits_num'],cut_credits_num,weo_credits_num))

df.head(30)

六、特征选择

df_columns = ["account_status","period","history_credit","credit_purpose","credit_limit","saving_account","person_employee",
           "income_installment_rate","marry_sex","other_debtor","address","property","age","installment_plans","housing","credits_num","job","dependents","have_phone","foreign_worker"]
list_iv = []
for i in df_columns:
    iv = 0
    only = df[i].unique()
    for j in only:
        good_rate = len(df.loc[(df[i]==j)&(df['target']==0)])/len(df[df['target']==0])
        bad_rate = len(df.loc[(df[i]==j)&(df['target']==1)])/len(df[df['target']==1])
        iv = iv+(j*(good_rate-bad_rate))
    list_iv.append(iv)
# list_iv
for i in range(len(list_iv)):
    print(f"列：{df_columns[i]},  iv=:{list_iv[i]}")

可视化更清晰

columns1 = ["account_status","period","history_credit","credit_purpose","credit_limit","saving_account","person_employee",
           "income_installment_rate","marry_sex","other_debtor","address","property","age","installment_plans","housing","credits_num","job","dependents","have_phone","foreign_worker"]
list_iv
#创建按一个以columns1为索引，list_iv为值的Series，便于我们画图
iv_plot = pd.Series(list_iv,index = columns1,name = "iv")
iv_plot = iv_plot.sort_values()
#可视化一下IV值排行（从小到大）
plt.figure(figsize = (25 ,7))
plt.bar(iv_plot.index ,iv_plot.values ,color = '#3beeb5')
# 对x轴进行翻转，竖向显示
plt.xticks(rotation=90, fontsize=14)
for a ,b in zip(iv_plot.index ,iv_plot.values.round(4)):
    plt.text(a ,b + 0.01 ,b ,ha = 'center' ,va = 'bottom')

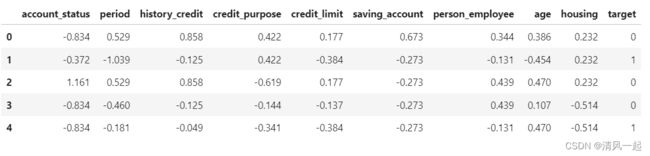
我只选取iv值大于0.1的变量作为特征变量，因此选取出以下变量

#剩下的目标变量
data = df[["account_status","period","history_credit","credit_purpose","credit_limit","saving_account","person_employee",
           "age","housing","target"]]
data.head()

七、Logistic回归模型构建

7.1.划分训练集和测试集

from sklearn import model_selection as cv
data_train_woe, data_test_woe = cv.train_test_split(df, test_size=0.2, random_state=10, stratify=df.target)

7.2.探索模型最优参数及训练模型

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
##训练模型
####取出训练数据与测试数据
x_train = np.array(data_train_woe[[i for i in data_train_woe.columns if i!='target']])
y_train = np.array(data_train_woe.target)

x_test = np.array(data_test_woe[[i for i in data_test_woe.columns if i!='target']])
y_test = np.array(data_test_woe.target)

##网络搜索查找最优参数
lr_param = {'C': [0.01, 0.1, 0.2, 0.5, 1, 1.5, 2],
            'class_weight': [{1: 1, 0: 1}, {1: 2, 0: 1}, {1: 3, 0: 1}, 'balanced'],
            'max_iter': range(10,100,10)}

##逻辑回归模型
lr_gsearch = GridSearchCV(
    estimator=LogisticRegression(random_state=0, fit_intercept=True, penalty='l2'),
    param_grid=lr_param, cv=5, scoring='f1', n_jobs=-1, verbose=2)

##执行超参数优化 
lr_gsearch.fit(x_train, y_train)
print('logistic model best_score_ is {0},and best_params_ is {1}'.format(lr_gsearch.best_score_,
                                                                         lr_gsearch.best_params_))

##用最优参数，初始化Logistic模型
LR_model_2 = LogisticRegression(C=lr_gsearch.best_params_['C'], penalty='l2',
                                class_weight=lr_gsearch.best_params_['class_weight'],
                                max_iter=lr_gsearch.best_params_['max_iter'])
##训练Logistic模型
LR_model_fit = LR_model_2.fit(x_train, y_train)

print ('逻辑回归的准确率为：{0:.2f}%'.format(LR_model_fit.score(x_test, y_test) *100))

八、模型检验

8.1.测试集预测值与真实的好坏样本分布图

from sklearn.metrics import precision_recall_curve
#预测概率值
y_score_test = LR_model_fit.predict_proba(x_test)[:,1]
##计算不同概率阈值的精确召回对
test_precision,test_recall,thresholds=precision_recall_curve(y_test,y_score_test)
##区分测试集中真实的好坏样本数据
df_pre_all = pd.DataFrame({'y_score':y_score_test,'y_test':y_test})
df_pre_good = df_pre_all.loc[df_pre_all["y_test"]==0,]
df_pre_good = df_pre_good.sort_values(["y_score"])
df_pre_bad = df_pre_all.loc[df_pre_all["y_test"]==1,]
df_pre_bad = df_pre_bad.sort_values(["y_score"])
##结果绘图
plt.figure(figsize=(10,6))
plt.rcParams["font.family"]=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.hist(df_pre_good["y_score"],bins=100,color='r',alpha=0.5,rwidth=0.6,density=True,label='好样本')
plt.hist(df_pre_bad['y_score'],bins=100,color='b',alpha=0.5,rwidth=0.6,density=True,label='坏样本')
plt.legend()
plt.title('好坏样本分布直方图')
plt.xlabel('predict y proba')
plt.ylabel('count')
plt.show()

8.2.混淆矩阵及PR曲线

from sklearn.metrics import confusion_matrix
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score
##计算混淆矩阵、P、R 与f1-score
y_pred = LR_model_fit.predict(x_test)  #返回预测分类值数组
cnf_matrix = confusion_matrix(y_test, y_pred, labels=[0,1]) #建立混淆矩阵 
recall_value = recall_score(y_test, y_pred)
precision_value = precision_score(y_test, y_pred)
acc = accuracy_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
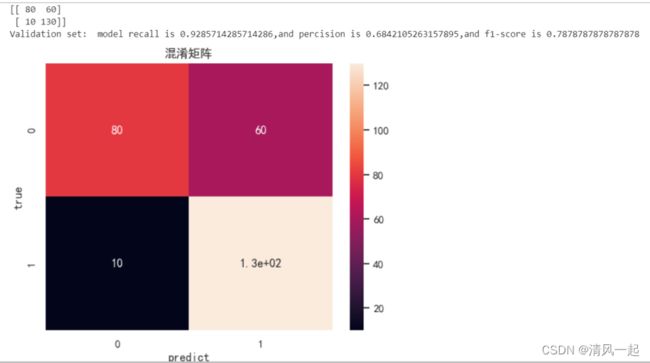
print(cnf_matrix)
print('Validation set:  model recall is {0},and percision is {1},and f1-score is {2}'.format(recall_value,
             precision_value,f1)) 
###绘制混淆矩阵
f,ax=plt.subplots()
sns.heatmap(cnf_matrix,annot=True,ax=ax) #画热力图
ax.set_title('混淆矩阵') #标题
ax.set_xlabel('predict') #x轴
ax.set_ylabel('true') #y轴
plt.show()

##绘制pr曲线，需要用到上面计算的不同概率阈值的精确召回对
#计算不同概率阈值的精确召回对
test_precision,test_recall,thresholds=precision_recall_curve(y_test,y_score_test)
plt.figure(figsize=(12,6))
lw = 2
fontsize_1 = 16
plt.plot(test_recall,test_precision,color='darkorange',lw=lw)
plt.plot([0,1],[0,1],color='navy',lw=lw,linestyle='--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.05])
plt.xticks(fontsize=fontsize_1)
plt.yticks(fontsize=fontsize_1)
plt.xlabel('Recall',fontsize=fontsize_1)
plt.ylabel('Precision',fontsize=fontsize_1)
plt.title('PR曲线',fontsize=fontsize_1)
plt.show()

#给各变量赋值
# TP：表示预测为坏样本，实际上也是坏样本，正确拒绝的样本数 (130)
TP = cnf_matrix[1,1]
# FP：表示预测为坏样本，实际上是好样本，错误拒绝的样本数 (60)
FP = cnf_matrix[0,1]
# FN：表示预测为好样本，实际上是坏样本，漏报的样本，被错误准入的样本数 (10)
FN = cnf_matrix[1,0]
# TN：表示预测为好样本，实际上是好样本，正确准入的样本数 (80)
TN = cnf_matrix[0,0]
#我们知道在评分卡业务场景下更关注坏账率和通过率，理想的评分卡模型是最大化通过率，最小坏账率
pt = (FN+TN)/(FN+TN+TP+FP)#通过率
bd = FN/(FN+TN) #坏账率
E = (FN+FP)/(FN+FP+TP+TN) #错误率
Acc = (TP+TN)/(FN+FP+TP+TN) #精度
Recall = TP/(TP+FN)  #召回率 ：即所有坏样本中找到多少坏样本
Precisoin = TP/(TP+FP) #精准率：衡量所有模型预测为正例的样本中真实为正例的概率（一部分好样本预测成坏样本了）

print(f"通过率为:pt = {pt}")
print(f"坏账率为:bd = {bd}")
print(f"错误率为:E = {E}")
print(f"精度为:Acc = {Acc}")
print(f"召回率为:Recall = {Recall}")
print(f"精确率为:Precisoin = {Precisoin}")

#PR曲线中，我们求平衡点（BEP）来衡量，BEP越大，模型性能越好，更好的指标是F1
F1 = (2*Precisoin*Recall)/(Precisoin+Recall)
print(F1)

8.3.ROC曲线

from sklearn.metrics import roc_curve
from sklearn.metrics import auc
#真阳性率（TPR）,假阳性率（FPR）
#我们目的是希望FPR尽可能小，TPR尽可能大
##计算TPR FPR ROC曲线 AUC AR gini等
fpr, tpr, thresholds = roc_curve(y_test, y_score_test)
roc_auc = auc(fpr, tpr)
ar = 2*roc_auc-1  #Gini系数时往往用ROC曲线曲线和中线围成的面积与中线之上面积的比例，也就是Gini=2AUC-1
gini = ar 
ks = max(tpr - fpr)
print('test set:  model AR is {0},and ks is {1},auc={2}'.format(ar,
             ks,roc_auc)) 
##绘制ROC曲线
plt.figure(figsize=(10,6))
lw = 2
fontsize_1 = 16
plt.plot(fpr,tpr,color='darkorange',lw=lw,label='ROC curve(area=%.2f)' % roc_auc)
plt.plot([0,1],[0,1],color='navy',lw=lw,linestyle='--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.05])
plt.xticks(fontsize=fontsize_1)
plt.yticks(fontsize=fontsize_1)
plt.xlabel('FPR',fontsize=fontsize_1)
plt.ylabel('TPR',fontsize=fontsize_1)
plt.title('ROC曲线',fontsize=fontsize_1)
plt.legend(loc='lower right',fontsize=fontsize_1)
plt.show()

九、评分卡构建

理论部分读者注意文章开头的知识准备

9.1.基础得分

lr = LR_model_fit
B = 20/np.log(2)
A = 600 + B*np.log(1/60)
base_score = A - B*lr.intercept_#lr.intercept_：截距
base_score

9.2.各评分结果

X = data_train_woe[[i for i in data_train_woe.columns if i!='target']]
df_fen = pd.DataFrame(columns = ['属性','区间','分数'])
list_key =[] #1.保存每一列的列名
list_value = []  #2.保存每一变量的区间（也叫分箱区间）
score_list=[] #3.保存每一个分箱的分数
list_key.append('基础得分')
list_value.append('无')
score_list.append(int(base_score))
for i,col in enumerate(X.columns):#[*enumerate(X.columns)]
    list2 = []
    list3 = []
    for key,value in woeall[col].items():
        # print(value)
        list2.append(value)
        list3.append(key)
    score = np.array(list2) * (-B*lr.coef_[0][i])
    for j in range(len(list3)):
        list_key.append(col)
        list_value.append(list3[j])
        score_list.append(score[j])
    list2 = []
    list3 = []
df_fen['属性'] = list_key
df_fen['区间'] = list_value
df_fen['分数'] = score_list
df_fen['分数取整'] = df_fen['分数'].round()    

df_fen.to_csv('评分卡分数.csv',header=True)

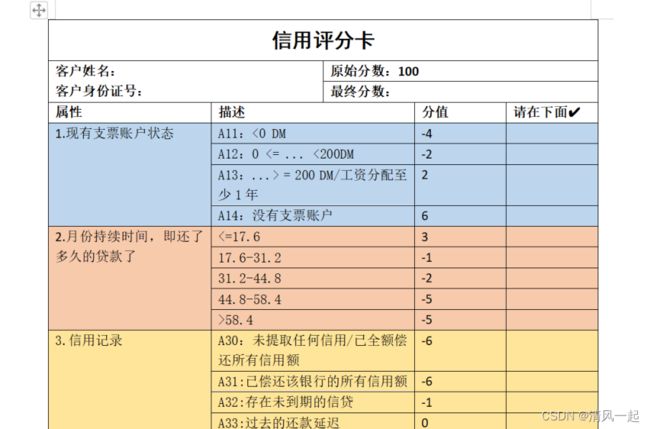
最后对评分卡进行规范化以及考虑使用该评分卡的用户的友好体验，对评分表进行优化:

1.增加没一个区间（分箱）的含义
2.基础分转化为100分
3.增加评分卡的使用说明
部分内容如下：

参考：
PYTHON机器学习之用逻辑回归制作评分卡（个人消费类贷款数据案例实战）
信用评分卡建模—基于German Credit德国信用数据集

《python金融大数据风控建模实战-基于机器学习》