【学习笔记】数据结构|算法 | Java——常见基本排序
数据结构的常见排序
| 插入排序—— 直接插入排序、折半插入排序和希尔排序 |
| 交换排序——冒泡排序‘、快速排序 |
| 选择排序——简单选择排序、堆排序 |
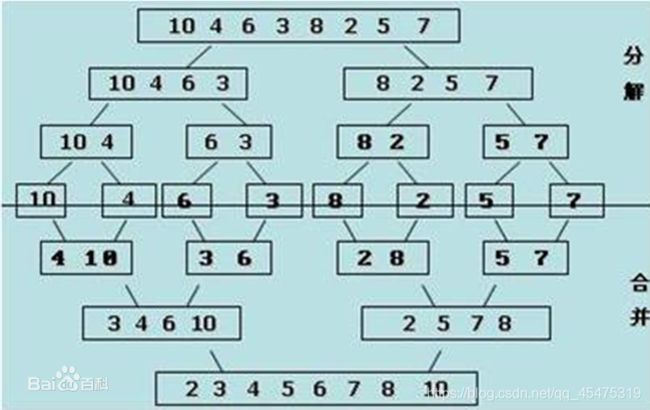
| 归并排序 |
| 计数数排序 |
| 基数排序 |
| 桶排序 |
1、冒泡排序
在数组范围内比较相邻的元素,如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做同样的工作,最后最大的元素就会冒泡到最后一个元素。
然后更新循环数组范围,因为最后一个元素不必比较,如此反复,直到没有要比较的相邻元素。
for(int i=0;i<arr.length;i++)
for(int j=0;j<arr.length-1-i;j++)
{
if(arr[j]>arr[j+1])
{
swap(arr,j,j+1);
}
}
2、选择排序
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
//外层for循环控制数组范围
for (int r = arr.length - 1; r >= 0; r--) {
//在范围内找到最大元素的值和下标
int index0fMax = 0;
int max = arr[0];
for (int i = 0; i <= r; i++) {
if (arr[i] > max) {
index0fMax = i;
max = arr[i];
}
}
//内层for循环完成,就找到了这次循环的范围内的最大值及其下标,然后与最后一个元素交换
swap(arr, index0fMax, r);
}
3、插入排序
像我们平时玩的手牌,乱序数组的元素像放在桌上的牌(待插入的元素),每次从桌上拿起手牌,都与手上的牌比较(手上的牌总是有序的),然后插入到正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。
static void insert(int[] arr)
{
int i,j,temp;
//第一层循环好比摸牌,从上到下一张一张去摸
for(i=1;i<arr.length;i++)
{
temp=arr[i];//新牌
//第二层循环将新牌从右往左与手上的牌比较
for(j=i-1;j>=0&&arr[j]>temp;j--)
{
arr[j+1]=arr[j];//后移
}
//新手牌放到合适的位置
arr[j+1]=temp;
}
}
4、希尔排序-(缩小增量排序)
希尔排序是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是把数组按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个数组恰被分成一组,算法便终止。
static void shellSort(int[] arr)
{ //不断地缩小增量
for(int interval=arr.length/2;interval>0;interval=interval/2)
{
//增量为i的插入排序
for(int i=interval;i<arr.length;i++){
int target=arr[i];//target为将要插入的元素
int j=i-interval;//j=0,j总是指向已排好序的元素的最后一个
while (j>-1&&target<arr[j]){//元素后移留出相应的位置
arr[j+interval]=arr[j];
j-=interval;
}
arr[j+interval]=target;
}
}
}
分治法
-
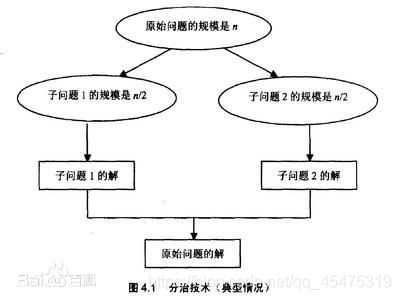
分治法(divide and conquer,D&C) :将原问题划分成若干个规模较小而结构与原问题一致的子问题;递归地解决这些子问题然后再合并其结果,就得到原问题的解。
-
容易确定运行时间,是分治算法的优点之一。
-
分治模式在每一层递归上都有三个步骤
分解(Divide) :将原问题分解成一系列子问题;
解决(Conquer) :递归地解各子问题。若子问题足够小,则直接有解;
合并(Combine):将子问题的结果合并成原问题的解。 -
分治的关键点
原问题可以一直分解为形式相同子问题,当子问题规模较小时,可自然求解,如一-个元素本身有序
子问题的解通过合并可以得到原问题的解
子问题的分解以及解的合并一定是比较简单的,则分解和合并所花的时间可能超出暴力解法,得不偿失
快速排序重点在划分
归并排序重点在合并
5、快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
-
分解:数组A[p…r]被划分为两个子数组A[p. .q-1]和A[q+1,r],使得A[q]为大小居中的数,左侧A[p. .q-1]中的每个元素都小于等于它,而右侧A[q+1,r]中的每个元素都大于等于它。其中计算下标q也是划分过程的一部分。
-
解决:通过递归调用快速排序,对子数组A[p. .q-1]和A[q+1,r]进行排序
-
合并:因为子数组都是原址排序的,所以不需要合并,数组A[p. .r]已经有序
那么,划分就是问题的关键
两种方法
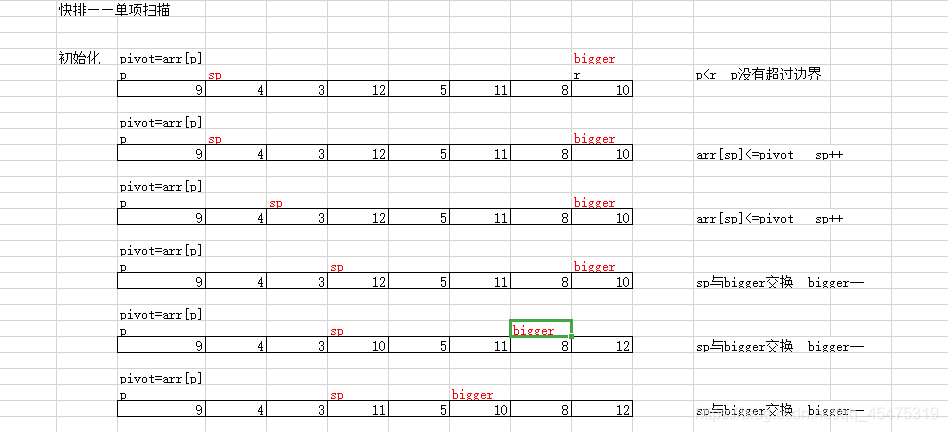
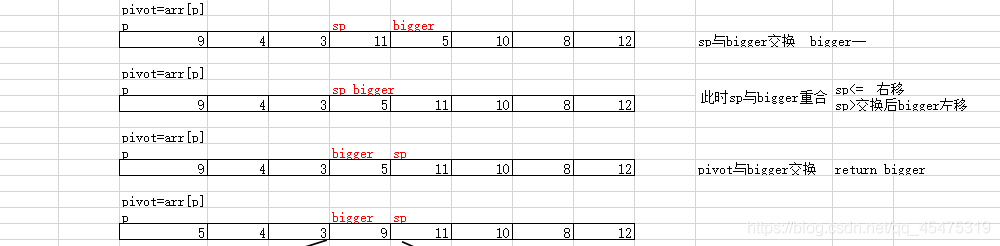
1、单向扫描法
算法设计思路:
- 用两个指针将数组划分为三个区间
- 扫描指针(scan_pos)左边是确认小于等于主元的
- 扫描指针到某个指针(next_bigger_pos)中间为未知的,因此我们将第二个指针(next_bigger_pos) 称为未知区间末指针,末指针的右边区间为确认大于主元的元素
在这里插入图片描述
private static void quickSort(int[] arr1,int p,int r) {
if(p<r){
int q=partition(arr1,p,r);
quickSort(arr1,p,q-1);
quickSort(arr1,q+1,r);
}
}
public static int partition(int[] arr1,int p,int r)
{
int pivot=arr1[p];
int sp=p+1;
int bigger=r;
while (sp<=bigger)
{
if(arr1[sp]<=pivot)
{
sp++;
}
else {
swap(arr1,sp,bigger);
bigger--;
}
}
swap(arr1,bigger,p);
return bigger;
}
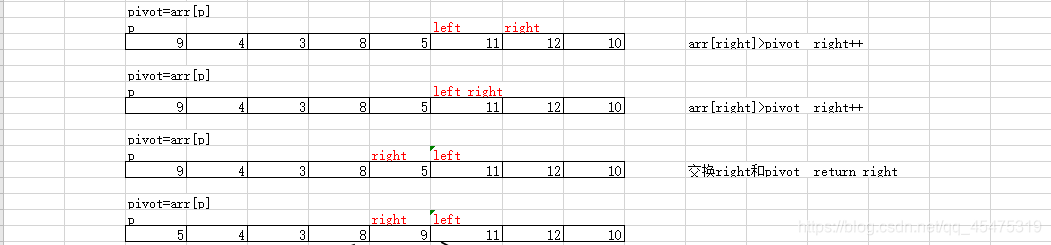
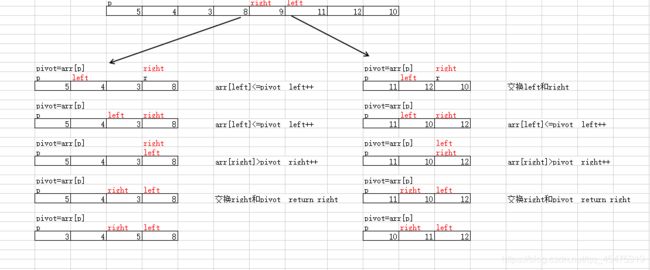
2、双向扫描法
双向扫描的思路是,头尾指针往中间扫描,从左找到大于主元的元素,从右找到小于等于主元的元素二者交换,继续扫描,直到左侧无大元素,右侧无小元素
private static void quickSort2(int[] arr1,int p,int r) {
if(p<r){
int q=partition2(arr1,p,r);
quickSort2(arr1,p,q-1);
quickSort2(arr1,q+1,r);
}
}
public static int partition2(int[] arr,int p,int r)
{
int pivot=arr[p];
int left=p+1;
int right=r;
//left不停往右走,直到遇到大于主元元素
while (left<=right) {
while (left<=right&&arr[left] <= pivot) left++;
while (left<=right&&arr[right] > pivot) right--;
if(left<right)
swap(arr, left, right);
}
swap(arr,p,right);
return right;
}
6、归并排序
- 归并排序(Merge Sort)算法完全依照了分治模式
分解:将n个元素分成各含n/2个元素的子序列;
解决:对两个子序列递归地排序;
合并:合并两个已排序的子序列以得到排序结果
和快排不同的是
归并的分解较为随意
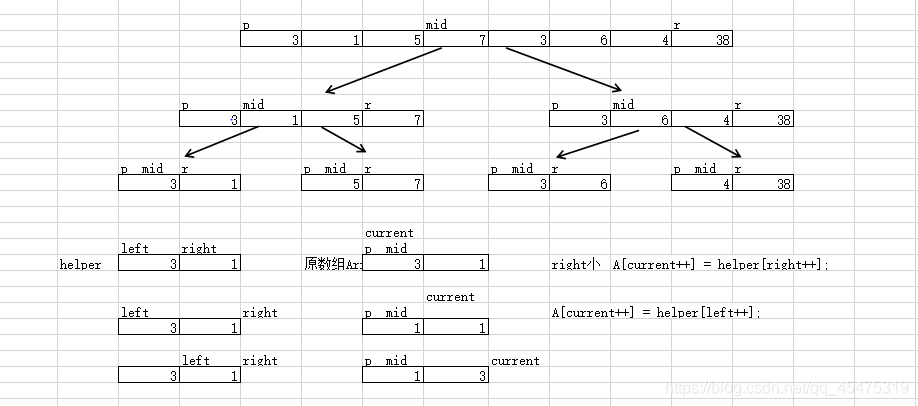
重点是合并 - 归并操作的工作原理如下:
第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置
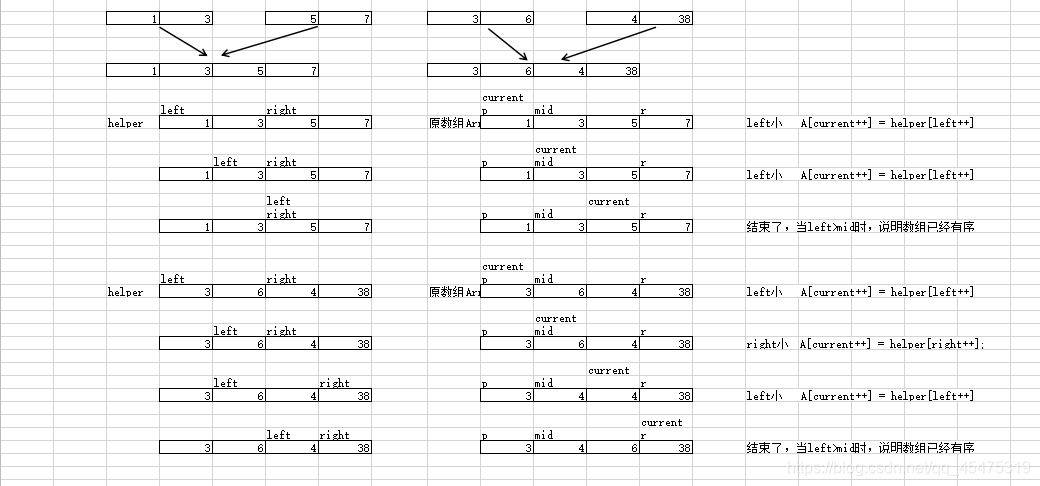
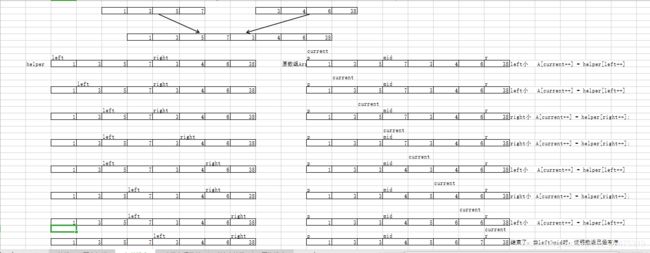
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针超出序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
//创建辅助数组
static int[] helper;
public static void sort(int[] Arr){
helper=new int[Arr.length];
sort(Arr,0,Arr.length-1);
}
public static void sort(int[]Arr,int p,int r){
if(p<r)
{
int mid=p+((r-p)>>1);//将数组从中间分成两段
sort(Arr,p,mid);//对左厕排序
sort(Arr,mid+1,r);//对右侧排序
merge(Arr,p,mid,r);//合并
}
}
public static void merge(int[] Arr,int p,int mid,int r){
//将原数组拷贝到辅助数组中
System.arraycopy(Arr,p,helper,p,r-p+1);
//辅助数组的两个指针
int left=p;int right=mid+1;//分别指向分半数组左右的头元素
//原始数组的指针
int current=p;
while(left<=mid&&right<=r)//保证left和right不越界
{
if (helper[left]<=helper[right])//左边小
{
Arr[current++]=helper[left++];
}else {
Arr[current++]=helper[right++];//右变小
}
}
while (left<=mid)//考虑right超出边界,left还没到边界
{
Arr[current++]=helper[left++];
}
7、堆排序
算法思路:1. 堆化:反向调整使得每个子树都是大顶堆或者小顶堆
2. 按序输出元素:把堆顶和最末元素对调,然后调整堆顶元素
大顶堆——正序输出
小顶堆——逆序输出
小顶堆排序
public static void MinHeap(int[] A,int n){
for(int i=n/2-1;i>=0;i--)
{
MinHeapFixDown(A,i,n);//对每个根结点(i)进行堆化
}
}
//进行局部堆化
static void MinHeapFixDown(int[] A,int i,int n)
{
//找到左右孩子
int left=2*i+1;//左孩子
int right=2*i+2;//右孩子
if(left>=n){//左孩子越界,i就是叶子节点,退出递归
return ;
}
//====min指向左右孩子中较小的一个=========
int min=left;
if(right>=n){
min=left;
}else{
//左右孩子没有越界
if(A[right]<A[left])
{
min=right;
}
}
//====min指向左右孩子中较小的一个=========
//如果A[i]比两个孩子都要小,不用调整
if(A[i]<=A[min])
{
return ;
}
//否则,找到两个孩子中较小的,和i比较
int temp=A[i];
A[i]=A[min];
A[min]=temp;
//小孩子那个位置的值发生变化,i变更为小孩子那个位置,递归调整
MinHeapFixDown(A,min,n);
}
//按序输出
static void sort(int[] A,int n){
//先对A进行堆化
MinHeap(A,n);
for(int x=n-1;x>=0;x--) {
//把堆顶,0号元素和最后一个元素对调(对调就不满足堆性质了)
swap(A, 0, x);
//缩小堆范围,对堆顶元素进行向下调整
MinHeapFixDown(A, 0, x);//每次交换影响的都是堆顶
}
}
8、计数排序
用辅助数组堆数组中出现的数字统计,元素转下标,下标转元素
public static void countSort(int[] A){
int max=A[0];
for(int item:A)
{
if(item>max)
max=item;
}
//创建辅助空间
int[] helper=new int[max+1];
for(int i:A)
helper[i]++;
int k=0;//数据回填的位置
for(int i=1;i<helper.length;i++)
{
while (helper[i]>0){
A[k++]=i;
helper[i]--;//防止漏掉重复的元素
}
}
}