博弈论——霍特林博弈(Hotelling Game)

0 引言

前一篇文章在特殊的伯特兰德博弈模型的基础上，解释了伯特兰德悖论，我们先简单回顾一下：
三个假设：
（1）各寡头厂商通过选择价格进行竞争；
（2）各寡头厂商生产的产品是同质的(完全可替代的)；
（3）寡头厂商之间也没有正式或非正式的串谋行为 。
内容和结论：
（1）伯特兰德模型是一个价格竞争模型；
（2）根据伯特兰德模型，谁的价格低谁就将赢得整个市场，而谁的价格高谁就将失去整个市场，因此寡头之间会相互削价，直至价格等于各自边际成本为止；
（3）根据伯特兰德均衡可以得到两个结论：a.寡头市场的均衡价格为：P=MC；b.寡头的长期经济利润为0。
博弈论——伯特兰德悖论(Bertrand Paradox)

当然，我们也在文章的末尾讨论了出现该悖论的三个原因就是因为三个假设，其中一个便是各寡头厂商生产的产品是同质的(完全可替代的)。如果企业生产的产品不完全相同，存在差异，则企业就可以通过产品的差异化进行竞争，避免直接的价格竞争。

也就是说解决这个悖论的方法之一就是引入产品的差异性，如果不同企业生产的产品是有差异的，替代弹性就不会是无限的,此时消费者对不同企业的产品有着不同的偏好,价格不是他们感兴趣的唯一变量，在这种情况下，均衡价格就不会是边际成本。

产品的差异性可以存在很多，比如包装、品牌、质量等等，这篇文章我们考虑一种特殊的差异——空间差异(Spatial differences)，这便是霍特林模型(Hotelling model)。

当然，空间差异也是有不同的，可能两家店在同一条直线街道上，也能在不是直线的街道上；可能两家店在街道的头尾，也可能都在街道中，所以根据空间差异不同，我们又可以进一步介绍霍特林模型的三种情况。

1 霍特林模型

在霍特林模型中，产品是同质的，但是在空间位置上有差异，因为不同位置上的消费者需要支付不同的运输成本，所以此时，顾客考虑的因素就有两点：价格、运输成本(旅行成本)。

很好理解，假设你家位于一条街道上，街头和街尾都有一家味道一样的冰淇淋店，这时候你要买冰淇淋的话，就会考虑这两家店的价格以及走到两家店的时间(路程)，那如果这条街道上从头到尾都有人家，那么其他人会考虑去哪里买呢？现在我们把这个问题抽象成一个数学问题，进一步讨论。

假设有一个长度为1的线性城市，消费者均匀地分布在[0,1]区间内。假定有两个商店出售同质的产品，商品同质表示就商品本身而言，能够带给消费者的效用(utility)是相同的。我们假设商店1、2出售的产品的效用均为U，并且效用U>旅行成本+价格。
每个商店单位产品的成本为c，消费者购买商品的旅行成本为t。

（1）case1：两家商店分别位于街道两端

假设两个商店分别位于街道的两端，商店1位于最左端，商店2位于最右端即商店1在x=0处，商店2在x=1处。住在x处的消费者，如果要去商店1消费，要花费$tx$的旅行成本；在商店2消费，要花费$t(1-x)$的旅行成本。假设所有消费者均购买一单位的产品，商店1的价格为$p_1$，商店2的价格为$p_2$，$D_i(p_1,p_2),i=1,2$为两个商店的需求函数。
所以消费者们从商品上获得的最终效用为商品效用-旅行成本-价格即
$$U_{final}=U-travelcost-price$$
因此，消费者选择商店1或者商店2的临界位置为消费者去两家店最终获得的效用相同即：
$$U_{final}^1=U_{final}^2$$
$$U-tx-p_1=U-t(1-x)-p_2$$
解得：
$$x^{\ast }=\frac{p_2-p_1+t}{2t}$$
所以，位于$x^{\ast }$左边的($x\in [0,x^{\ast })$)的消费者都会去商店1购买；位于$x^{\ast }$右边的($x\in (x^{\ast },1]$)的消费者都会去商店2购买；位于$x^{\ast }$处的消费者不论去哪个店最终效用都一样，称为无差别消费者位置。

也就是说双方的需求函数为(消费者服从[0,1]的均匀分布)：
$$D_1(p_1,p_2)={\int }_0^{x^{\ast }}1dx=x^{\ast }=\frac{p_2-p_1+t}{2t}$$
$$D_2(p_1,p_2)={\int }_{x^{\ast }}^{0}1dx=1-x^{\ast }=\frac{p_1-p_2+t}{2t}$$

解读：
(1)$D_1(p_1,p_2)$关于p1递减，关于p2递增，也就是说当商店1的价格变高时，商店1的需求量就下降；当商店2的价格变高时，商店1的需求量就上升。
$D_2(p_1,p_2)$是关于p2递减，关于p1递增的，解释也是类似。
(2)当p1=p2时，无差别消费者位置位于中间(x=1/2)处，此时商店1、2平分整个市场份额；
当p1>p2时，无差别消费者位置位于x=1/2的左边；
当p1

则两个商店的利润函数为
$${\pi }_1(p_1,p_2)=(p_1-c)D_1(p_1,p_2)=\frac{1}{2t}(p_1-c)(p_2-p_1+t)$$
$${\pi }_2(p_1,p_2)=(p_2-c)D_2(p_1,p_2)=\frac{1}{2t}(p_2-c)(p_1-p_2+t)$$
对利润函数求导为0：
$$\frac{\partial {\pi }_1(p_1,p_2)}{\partial p_1}=\frac{1}{2t}(p_2-2p_1+t+c)=0$$
$$\frac{\partial {\pi }_2(p_1,p_2)}{\partial p_2}=\frac{1}{2t}(p_1-2p_2+t+c)=0$$
解得博弈的均衡价格为：
$$p_1^{\ast }=p_2^{\ast }=c+t$$
两家店的均衡利润为：
$${\pi }_1^{\ast }={\pi }_2^{\ast }=\frac{t}{2}$$
我们将消费者的位置差异解释为产品差异，这个差异进一步可解释为消费者购买产品的旅行成本。旅行成本越高，产品的差异就越大，均衡价格就越大从而均衡利润也就越高。原因在于，随着旅行成本的上升，不同商店出售的产品之间的替代性下降，每个商店对附近的消费者的垄断力加强，商店之间的竞争越来越弱，消费者对价格的敏感度下降，从而每个商店的最优价格更接近于垄断价格。

（2）case2：两家商店在同一个位置
在case1中，假定两个商店分别位于街道的两端，事实上，均衡结果对于商店的位置是很敏感的。考虑一个极端的情况，假定两个商店位于同一个位置x，此时对于所有位置的消费者，他们到两家店的旅行成本都相同，所以对于任意一个消费者，不管他住哪，他去两家店的旅行成本都相同，也就是为两家店的空间差异不存在了（在同一个位置当然空间位置就没差异了）。此时，由于出售的是同质的产品，消费者又变成了只关心价格，该模型的唯一均衡就是伯特兰德均衡，即：
$$p_1^{\ast }=p_2^{\ast }=c$$
$${\pi }_1^{\ast }={\pi }_2^{\ast }=0$$
再次提醒，这里两家商店位于同一个位置，对于不同位置的消费者而言，旅行成本还是存在的，离商店远的旅行成本就高，离商店近的旅行成本就低。但如果从某一个消费者角度而言，这两家店在同一个位置，没有空间差异，不管去哪家店，该消费者的旅行成本都一样。

（3）case3：两家商店可以位于街道任意位置
Case3中，我们讨论商店位于任何位置的情况，这种情况其实是更一般的情况，根据这种情况的结论我们也可以去推得上述两个例子。
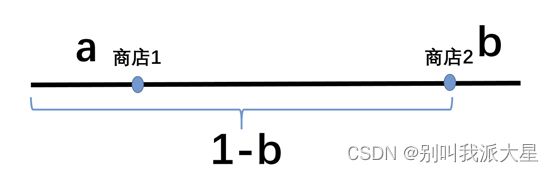
假定商店1位于$a\ge 0$，商店2位于$1-b(b\ge 0)$。为不失一般性,假定$1-(a+b)\ge 0$(即商店1位于商店2的左边)。如果旅行成本为二次式,即旅行成本为$t{d}^2$,这里$d$是消费者到商店的距离。同样，我们假设无差别消费者位置为x，x左边的消费者都在商店1消费，x右边的消费者都在商店2消费。

因此我们同样可以根据最终效用来计算x:
$$U_{final}^1=U_{final}^2$$
$$U-t(x^{\ast }-a{)}^2-p_1=U-t[(1-b)-x^{\ast }{]}^2-p_2$$
解得：
$$x^{\ast }=\frac{1-b+a}{2}+\frac{p_2-p_1}{2t(1-a-b)}$$
即$x<x^{\ast }$的消费者都在商店1买，$x>x^{\ast }$的消费者都在商店2买，$x=x^{\ast }$处为无差别消费者位置。
因此，可以得到需求函数分别为:
$$D_1(p_1,p_2)={\int }_0^{x^{\ast }}1dx=x^{\ast }=\frac{1-b+a}{2}+\frac{p_2-p_1}{2t(1-a-b)}$$
$$D_2(p_1,p_2)={\int }_{x^{\ast }}^{1}1dx=1-x^{\ast }=\frac{1+b-a}{2}+\frac{p_1-p_2}{2t(1-a-b)}$$
为了让结果有更好地解释性以及方便读者理解，我们进一步将结果改写为：
$$D_1(p_1,p_2)=a+\frac{1-b-a}{2}+\frac{p_2-p_1}{2t(1-a-b)}$$
$$D_2(p_1,p_2)=b+\frac{1-b-a}{2}+\frac{p_1-p_2}{2t(1-a-b)}$$
需求函数的第一项是商店自己的“地盘”(a是住在商店1左边的消费者，b是住在商店2右边的消费者)；第二项是位于两商店之间的消费者中靠近自己的一半，第三项代表需求对价格差异的敏感度。

则两个商店的利润函数为
$${\pi }_1(p_1,p_2)=(p_1-c)D_1(p_1,p_2)=(p_1-c)[a+\frac{1-b-a}{2}+\frac{p_2-p_1}{2t(1-a-b)}]$$
$${\pi }_2(p_1,p_2)=(p_2-c)D_2(p_1,p_2)=(p_2-c)[b+\frac{1-b-a}{2}+\frac{p_1-p_2}{2t(1-a-b)}]$$
同样，分别对p1、p2求导为0：
$$\frac{\partial {\pi }_1(p_1,p_2)}{\partial p_1}=0$$
$$\frac{\partial {\pi }_2(p_1,p_2)}{\partial p_2}=0$$
解得：
$$p_2-2p_1=-t(1-b+a)(1-a-b)-c$$
$$p_1-2p_2=-t(1+b-a)(1-a-b)-c$$
进一步求解关于$p_1$ 、$p_2$的二元一次方程，得：
$$p_1^{\ast }=c+\frac{1}{3}t(1-a-b)(3+a-b)$$
$$p_2^{\ast }=c+\frac{1}{3}t(1-a-b)(3+b-a)$$

根据这个一般模型的结论，我们再推导一下前文提到的两种情况。

• 商店在街道两端，此时a=b=0，则 $$p_1^{\ast }=c+t，p_2^{\ast }=c+t$$
• 商店在同一个位置，此时 a=1-b，则 $$p_1^{\ast }=p_2^{\ast }=c$$

两种情况的结论与前文推出的结论相同！