人工智能-深度学习计算：层和块

我们关注的是具有单一输出的线性模型。 在这里，整个模型只有一个输出。

注意，单个神经网络 （1）接受一些输入； （2）生成相应的标量输出； （3）具有一组相关 参数（parameters），更新这些参数可以优化某目标函数。

然后，当考虑具有多个输出的网络时， 我们利用矢量化算法来描述整层神经元。 像单个神经元一样，层（1）接受一组输入， （2）生成相应的输出， （3）由一组可调整参数描述。 当我们使用softmax回归时，一个单层本身就是模型。 然而，即使我们随后引入了多层感知机，我们仍然可以认为该模型保留了上面所说的基本架构。

对于多层感知机而言，整个模型及其组成层都是这种架构。 整个模型接受原始输入（特征），生成输出（预测）， 并包含一些参数（所有组成层的参数集合）。 同样，每个单独的层接收输入（由前一层提供）， 生成输出（到下一层的输入），并且具有一组可调参数， 这些参数根据从下一层反向传播的信号进行更新。

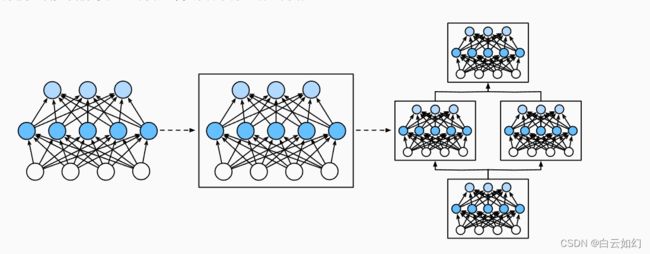
事实证明，研究讨论“比单个层大”但“比整个模型小”的组件更有价值。 例如，在计算机视觉中广泛流行的ResNet-152架构就有数百层， 这些层是由层组（groups of layers）的重复模式组成。 这个ResNet架构赢得了2015年ImageNet和COCO计算机视觉比赛 的识别和检测任务 (He et al., 2016)。 目前ResNet架构仍然是许多视觉任务的首选架构。 在其他的领域，如自然语言处理和语音， 层组以各种重复模式排列的类似架构现在也是普遍存在。

为了实现这些复杂的网络，我们引入了神经网络块的概念。 块（block）可以描述单个层、由多个层组成的组件或整个模型本身。 使用块进行抽象的一个好处是可以将一些块组合成更大的组件， 这一过程通常是递归的。 通过定义代码来按需生成任意复杂度的块， 我们可以通过简洁的代码实现复杂的神经网络。

 下面的代码生成一个网络，其中包含一个具有256个单元和ReLU激活函数的全连接隐藏层， 然后是一个具有10个隐藏单元且不带激活函数的全连接输出层。

import torch
from torch import nn
from torch.nn import functional as F

net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))

X = torch.rand(2, 20)
net(X)

tensor([[ 0.0343,  0.0264,  0.2505, -0.0243,  0.0945,  0.0012, -0.0141,  0.0666,
         -0.0547, -0.0667],
        [ 0.0772, -0.0274,  0.2638, -0.0191,  0.0394, -0.0324,  0.0102,  0.0707,
         -0.1481, -0.1031]], grad_fn=)

在这个例子中，我们通过实例化nn.Sequential来构建我们的模型， 层的执行顺序是作为参数传递的。 简而言之，nn.Sequential定义了一种特殊的Module， 即在PyTorch中表示一个块的类， 它维护了一个由Module组成的有序列表。 注意，两个全连接层都是Linear类的实例， Linear类本身就是Module的子类。 另外，到目前为止，我们一直在通过net(X)调用我们的模型来获得模型的输出。 这实际上是net.__call__(X)的简写。 这个前向传播函数非常简单： 它将列表中的每个块连接在一起，将每个块的输出作为下一个块的输入。