力扣第337题 打家劫舍 IIl c++ 附Java代码 暴力+记忆递推 或or 动态规划
题目
337. 打家劫舍 III
中等
相关标签
树 深度优先搜索 动态规划 二叉树
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
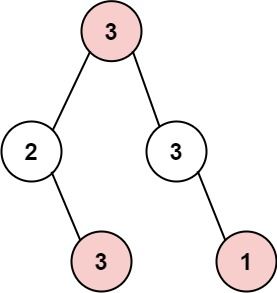
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示:
- 树的节点数在
[1, 104]范围内 0 <= Node.val <= 104
思路和解题方法一 (暴力解法+记忆递推)
先讲解纯暴力的代码超时(c++)
class Solution {
public:
int rob(TreeNode* root) { // rob函数接收一个TreeNode指针root作为参数,并返回一个整数值
if (root == NULL) return 0; // 如果root为空,直接返回0
if (root->left == NULL && root->right == NULL) return root->val; // 如果root没有左右孩子,直接返回root的值
int val1 = root->val; // 偷取父节点的金额
if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 如果存在左孩子,加上偷取左孩子的最大金额
if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 如果存在右孩子,加上偷取右孩子的最大金额
int val2 = rob(root->left) + rob(root->right); // 不偷取父节点的金额,考虑偷取左右孩子的最大金额
return max(val1, val2); // 返回偷取父节点和不偷取父节点两种情况下的最大金额
}
};
时间复杂度:
- 遍历一次数组,需要线性时间O(n)。
- 对于每个数,我们需要将其转换为字符串并计算各个位数上的平方和,这需要常数级的时间O(k),其中k是数字的位数。
- 因此,总时间复杂度为O(n*k),其中n是数组中数字的数量,k是最大数字的位数。
空间复杂度:
- 我们只使用了常数级的额外空间,因此空间复杂度为O(1)。
正确解法
- 用了递归的方式来计算二叉树节点的最大偷盗金额。在递归过程中,通过一个
unordered_map(哈希表)umap来记录已经计算过的结果,避免重复计算。- 首先判断二叉树是否为空,如果为空,则返回0。然后判断二叉树是否只有一个节点,如果是,则直接返回该节点的值。
- 接下来,检查
umap中是否已经有当前节点的计算结果,如果有,则直接返回之前计算的结果,避免重复计算。- 然后,我们开始考虑偷当前节点的情况。首先,将当前节点的值
root->val保存到val1中。接着,如果存在左子节点,将递归计算左子节点的左右孩子的最大值,并加到val1中。如果存在右子节点,同样地,将递归计算右子节点的左右孩子的最大值,并加到val1中。- 然后,我们考虑不偷当前节点的情况。计算左右子节点的最大值,并加到
val2中。- 最后,将计算得到的结果
val1和val2中的最大值存入umap中,以便后续使用,并返回最大值。- 该算法通过利用递归和动态规划的思想,避免了重复计算,从而提高了计算效率。
- 对于时间复杂度,每个节点只会被访问一次,因此总的时间复杂度为O(n),其中n是节点的数量。
复杂度
时间复杂度:
O(n)
对于时间复杂度,由于每一个节点只会被访问一次,因此总的时间复杂度为 O(n),其中 n 是节点的数量。
空间复杂度
O(n)
对于空间复杂度,除了存储二叉树结构本身所需要的空间外,还使用了
umap哈希表来记录已经计算过的结果。在最坏的情况下,umap中需要存储所有节点的结果,因此空间复杂度为 O(n)。
c++ 代码一
class Solution {
public:
unordered_map umap; // 记录计算过的结果
int rob(TreeNode* root) {
if (root == NULL) return 0; // 如果二叉树为空,返回0
if (root->left == NULL && root->right == NULL) return root->val; // 如果二叉树只有一个节点,返回该节点的值
if (umap[root]) return umap[root]; // 如果在umap中已经有记录,则直接返回之前计算的结果,避免重复计算
// 偷父节点
int val1 = root->val;
if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 如果存在左子节点,递归计算左子节点的左右孩子的最大值,并加到val1中
if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 如果存在右子节点,递归计算右子节点的左右孩子的最大值,并加到val1中
// 不偷父节点
int val2 = rob(root->left) + rob(root->right); // 递归计算左右子节点的最大值,并加到val2中
umap[root] = max(val1, val2); // 将计算得到的结果存入umap中,以便后续使用
return max(val1, val2); // 返回val1和val2中的最大值
}
};
思路和解题方法二 (动态规划)
- 首先定义了一个
rob函数,接收一个TreeNode类型的指针root,并返回一个整数值。- 在
rob函数中,调用了robTree函数来计算打家劫舍的结果。将结果保存在result向量中。- 最后,从
result向量中取出不偷根节点和偷根节点的两个值,返回其中较大的值作为结果。robTree函数接收一个TreeNode类型的指针cur,并返回一个长度为 2 的整数向量。- 如果当前节点
cur为空,说明到达了叶子节点,返回长度为 2 的全 0 向量。- 对于非空的当前节点,首先递归调用
robTree函数计算左子树和右子树的结果,分别存储在left和right向量中。- 考虑偷当前节点
cur,则不能偷左右节点。计算偷当前节点时,总值为当前节点值加上左子树不偷和右子树不偷的总值。- 考虑不偷当前节点
cur,则可以选择偷或不偷左右子树,取两者中较大的情况。总值为左子树中较大的偷或不偷的值加上右子树中较大的偷或不偷的值。- 最后,将不偷和偷的总值存储在长度为 2 的向量中,返回该向量作为结果。
复杂度
时间复杂度:
O(n)
时间复杂度:该算法使用了递归实现,每个节点只参与到两个子树的计算中,因此时间复杂度为 O(n),其中 n 是二叉树的节点数。
空间复杂度
O(n)
空间复杂度:除了存储二叉树结构本身所需要的空间外,只使用了长度为 2 的向量来保存每个节点的结果,因此空间复杂度为 O(n)。
c++ 代码
class Solution {
public:
int rob(TreeNode* root) {
vector result = robTree(root);
return max(result[0], result[1]);
}
// robTree函数接收一个TreeNode类型的指针cur, 并返回一个长度为2的vector
// 第一个元素表示不偷当前节点时,子树所能获得的最大收益,第二个元素表示偷当前节点时,子树所能获得的最大收益。
vector robTree(TreeNode* cur) {
if (cur == NULL) return vector{0, 0}; // 如果当前节点为空,则返回{0,0}
vector left = robTree(cur->left); // 递归计算左子树的结果
vector right = robTree(cur->right); // 递归计算右子树的结果
// 偷cur,那么就不能偷左右节点。
int val1 = cur->val + left[0] + right[0]; // 当前节点被偷时,左右子节点必须都不能被偷,因此val1等于当前节点值加上左右子树不偷的值(left[0], right[0])
// 不偷cur,那么可以偷也可以不偷左右节点,则取较大的情况
int val2 = max(left[0], left[1]) + max(right[0], right[1]); // 当前节点不被偷时,左右子节点可以选择偷或不偷,因此val2等于左右子树中所能获得的最大收益(max(left[0], left[1]), max(right[0], right[1]))之和
return {val2, val1}; // 返回长度为2的vector,第一个元素为不偷该节点时所能获得的最大收益,第二个元素为偷该节点时所能获得的最大收益
}
};
Java代码
递归去偷,会超时:该算法使用递归实现,分别考虑偷当前节点和不偷当前节点,然后分别递归计算左子树和右子树的结果。时间复杂度为 O(2^n),其中 n 是树的高度,会超时。
递归去偷,记录状态:该算法使用递归实现,将结果记录在 HashMap 中,遇到相同的节点时直接从 memo 中取值,避免重复计算。时间复杂度为 O(n),其中 n 是树的节点数。
状态标记递归:该算法同样使用递归实现,用数组 res 来记录当前节点偷或者不偷的情况下的最大价值,res[0] 表示不偷 root 节点时的最大价值,res[1] 表示偷 root 节点时的最大价值。在递归过程中,分别计算当前节点不偷和偷的情况下,左右子树可以偷或不偷的最大值。时间复杂度为 O(n),其中 n 是树的节点数。
class Solution {
// 1.递归去偷,会超时
public int rob(TreeNode root) {
if (root == null)
return 0;
int money = root.val;
if (root.left != null) {
money += rob(root.left.left) + rob(root.left.right);
}
if (root.right != null) {
money += rob(root.right.left) + rob(root.right.right);
}
return Math.max(money, rob(root.left) + rob(root.right));
}
// 2.递归去偷,记录状态
// 将结果记录在 memo HashMap 中,遇到相同的节点时直接从 memo 中取值,避免重复计算
public int rob1(TreeNode root) {
Map memo = new HashMap<>();
return robAction(root, memo);
}
int robAction(TreeNode root, Map memo) {
if (root == null)
return 0;
if (memo.containsKey(root)) // memo 中已经记录了 root 的值,直接返回它
return memo.get(root);
int money = root.val;
if (root.left != null) {
money += robAction(root.left.left, memo) + robAction(root.left.right, memo);
}
if (root.right != null) {
money += robAction(root.right.left, memo) + robAction(root.right.right, memo);
}
int res = Math.max(money, robAction(root.left, memo) + robAction(root.right, memo));
memo.put(root, res); // 将 root 当前的结果放入 memo 中
return res;
}
// 3.状态标记递归
// 用数组 res 来记录当前节点偷或者不偷的情况下的最大价值
// res[0] 表示不偷 root 节点时的最大价值,res[1] 表示偷 root 节点时的最大价值
public int rob2(TreeNode root) {
int[] res = robAction1(root);
return Math.max(res[0], res[1]);
}
int[] robAction1(TreeNode root) {
int res[] = new int[2];
if (root == null)
return res;
int[] left = robAction1(root.left);
int[] right = robAction1(root.right);
// 当前节点不偷时,左右子树可以偷或不偷
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
// 当前节点偷时,左右子树必须都不偷
res[1] = root.val + left[0] + right[0];
return res;
}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。