2021年8月LeetCode每日一题
每日一题
- 2021年8月
-
- (DP-中等)最长回文子序列
- (数学-困难)数字中 1 的个数
- (模拟-中等)统计不开心的朋友
- (DP-中等)出界的路径数
- (深搜|状压DP)-中等)优美的排列
-
- 深搜
- 状压DP
- (模拟-简单)学生出勤记录 I
- (DP - 困难)学生出勤记录 II
- (模拟-简单)反转字符串中的元音字母
- (模拟-简单)反转字符串 II
- (模拟-中等)压缩字符串
- (数学-中等)逃脱阻碍者
- (模拟-简单)获取生成数组中的最大值
- (图论-中等)K站中转内最便宜的航班
- (搜索-中等)所有可能的路径
- (贪心-中等)救生艇
- (模拟-困难)数据流的中位数
-
- 双端队列
- 双指针
- (前缀和-简单)一维数组的动态和
- (前缀和-简单)所有奇数长度子数组的和
- (前缀和+二分-中等)按权重随机选择
- (差分前缀和-中等)航班预订统计
2021年8月
(DP-中等)最长回文子序列
题目描述:
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
题目链接
思路: 局部最优,可以推广到全局最优,很显然是动态规划
- dp[ i ][ j ] 表示从i到j最长回文子序列的最大长度。
- 如果s[ i ] == s[ j ] 那么dp[ i ][ j ] = dp[i + 1][j - 1] + 2。这两个相等,所以的,最大长度等于更小范围内的最大子序列长度加2
- 如果s[ i ] != s[ j ] 那么dp[ i ][ j ] = max(dp[i + 1][ j ],d[ i ][ j - 1])。这两个不相等,最大长度等于包括两边任意一个最大长度最为它的最大长度。
- 有点像区间DP,从小范围更新到大范围。这里只需要注意一下循环的顺序就好。
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
vector<vector<int> > dp(n + 1,vector<int>(n + 1,0));
for (int i = 0; i < n; i ++) dp[i][i] = 1;
for (int i = n-2; i >= 0; i --){
for (int j = i + 1; j < n; j ++){
if (s[i] == s[j])dp[i][j] = dp[i+1][j-1] + 2;
else dp[i][j] = max(dp[i][j-1],dp[i+1][j]);
}
}
return dp[0][n-1];
}
};
(数学-困难)数字中 1 的个数
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
0 <= n <= 2*10^9
题目链接
思路: 思路借鉴大佬
把n各个位上为1的数量相加,即为1出现的总次数。
把n设为x位,把n的第i为记为 ni,那么n可以写成nxnx-1…n2n1。
- 设ni 为 当前位 ,记为 cur
- 称ni-1ni-2…n2n1 为 ni 的 低位,记为 low
- 称nx-1nx-2…ni+2ni+1 为 ni 的 高位,记为 high
- 称 10i 为 位因子,记为 digit
对cur分情况讨论:
1. 当 cur 为 0 时:此时1的出现个数只由high决定,计算公式为: h i g h × d i g i t high×digit high×digit
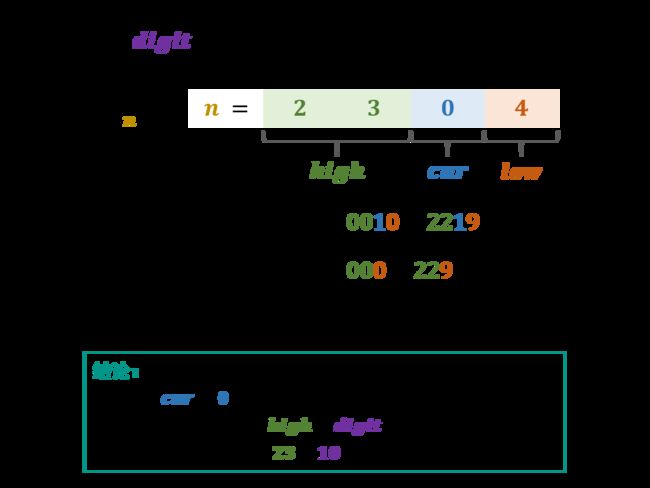
2. 当 cur 为 1 时:此时1的出现个数由高位的high和低位的low决定,计算公式为: h i g h × d i g i t + l o w + 1 high×digit + low + 1 high×digit+low+1

3. 当 cur 为 2,3,4,5,6,7,8,9 时:此时1的出现个数只由high决定,计算公式为: ( h i g h + 1 ) × d i g i t (high+ 1)×digit (high+1)×digit

因此从低位地推到高位,循环计数,即为答案。
循环次数为n的位数,所以时间复杂度为O( log N \log_N logN)
typedef long long LL;
class Solution {
public:
int countDigitOne(int n) {
LL digit = 1;
int res = 0;
int high = n / 10, cur = n % 10, low = 0;
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
};
(模拟-中等)统计不开心的朋友

思路:今天的比较简单 题目链接
(x,y)和(u,v)
比较四种情况:符合条件就标记一下(用标记是因为直接统计会有重复计算的情况)
- (x,u)和(x,y)且上(u,x)和(u,v)
- (x,v)和(x,y)且上(v,x)和(v,u)
- (y,u)和(y,x)且上(u,y)和(u,v)
- (y,v)和(y,x)且上(v,y)和(v,u)
class Solution {
public:
int unhappyFriends(int n, vector<vector<int>>& pes, vector<vector<int>>& pas) {
vector<vector<int> > rank(510,vector<int>(510,0));
vector<int> vis(510,0);
int t = pas.size();
for (int i = 0; i < n; i ++){
int m = pes[i].size();
int cnt = 600;
for (int j = 0; j < m; j ++){
rank[i][pes[i][j]] = cnt--;
}
}
int res = 0;
for (int i = 0; i < t; i ++){
int x = pas[i][0],y = pas[i][1];
for (int j = i+1; j < n/2; j ++){
int u = pas[j][0],v = pas[j][1];
if ((rank[x][u] > rank[x][y])&&(rank[u][x] > rank[u][v])){
vis[x] = 1;
vis[u] = 1;
}
if ((rank[x][v] > rank[x][y])&&(rank[v][x] > rank[v][u])){
vis[x] = 1;vis[v] = 1;
}
if ((rank[y][u] > rank[y][x])&&(rank[u][y] > rank[u][v])){
vis[y] = 1;vis[u] = 1;
}
if ((rank[y][v] > rank[y][x])&&(rank[v][y] > rank[v][u])){
vis[y] = 1;vis[v] = 1;
}
}
}
for (int i = 0; i < n; i ++){
if (vis[i])res++;
}
return res;
}
};
(DP-中等)出界的路径数

思路:动态规划 题目链接
遇到动态规划就没有做出来过 我不认命
dp[k][i][j] 表示走k步到[i,j]位置的最大方案 初值dp[0][startRow][startColumn] = 1走到初始位置方案数就是 1
当从dp[k][i][j] 走到 dp[k+1][i+x][j+y]
- 如果i+x和j+y没有出界,那么dp[k+1][i+x][j+y] = (dp[k+1][i+x][j+y] + dp[k][i][j])%MOD 用当前dp[k][i][j] 加上从其他地方转移来的 dp[k+1][i+x][j+y] 更新到当前 dp[k+1][i+x][j+y] 理解这里,容易更好的理解下面优化空间(降一维空间)
- 如果i+x和j+y出界了,那么就该记录答案了 res = (res + dp[k][i][j])%MOD
const int MOD = 1e9+7;
class Solution {
public:
int findPaths(int m, int n, int maxMove, int r, int c) {
vector<vector<int> > pos = {{0,-1},{1,0},{0,1},{-1,0}};
vector<vector<vector<int>>> dp(maxMove+1,vector<vector<int>>(m,vector<int>(n,0)));//maxMove+1防止k+1越界
int res = 0;
dp[0][r][c] = 1;
for (int k = 0; k < maxMove; k ++){
for (int i = 0; i < m; i ++){
for (int j = 0; j < n; j ++){ //注意m和n不要搞反了
if (dp[k][i][j]){
for(auto &p : pos){
int x = i + p[0],y =j + p[1];
if (x >= 0 && x < m && y >= 0 && y < n)
dp[k+1][x][y] = (dp[k][i][j] + dp[k+1][x][y])%MOD;
else
res = (res + dp[k][i][j])%MOD;
}
}
}
}
}
return res;
}
};
可以发现判断条件if (x >= 0 && x < m && y >= 0 && y < n) 和 k 没有关系,也就是说结果和 k 也没有关系,那我们是不是可以把去掉 k 那一维数组,空间复杂度又可以降一维。
const int MOD = 1e9+7;
class Solution {
public:
int findPaths(int m, int n, int maxMove, int r, int c) {
vector<vector<int> > pos = {{0,-1},{1,0},{0,1},{-1,0}};
vector<vector<int> > dp(m,vector<int>(n,0));
int res = 0;
dp[r][c] = 1;
for (int k = 0; k < maxMove; k ++){
vector<vector<int> > tp(m,vector<int>(n,0)); //滚动更新数组
for (int i = 0; i < m; i ++){
for (int j = 0; j < n; j ++){
if (dp[i][j]){
for(auto &p : pos){
int x = i + p[0],y =j + p[1];
if (x >= 0 && x < m && y >= 0 && y < n)
tp[x][y] = (dp[i][j] + tp[x][y])%MOD;
else
res = (res + dp[i][j])%MOD;
}
}
}
}
dp = tp; //更新数组
}
return res;
}
};
(深搜|状压DP)-中等)优美的排列

我的第一想法也是深搜,但是时间复杂度为n的阶乘,15的阶乘 = 1307674368000,所以觉得会超时,就没写,但是看了官方的答案发现确实深搜,好像 在LeetCode时间复杂度O(n!)也能过。
深搜
class Solution {
public:
vector<vector<int> > pre;
vector<int> vis;
int res = 0;
void dfs(int index,int n){
if (index == n + 1){
res++;
return;
}
for (int i = 0; i < pre[index].size(); i ++){
if (!vis[pre[index][i]]){
vis[pre[index][i]] = 1;
dfs(index+1,n);
vis[pre[index][i]] = 0;
}
}
}
int countArrangement(int n) {
pre.resize(n+1);
vis.resize(n+1);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= n; j ++)
if (i % j == 0 || j % i == 0){
pre[i].push_back(j);
}
dfs(1,n);
return res;
}
};
状压DP
我就解释一下官方的题解

时间复杂度O(2n) ,完全在1秒内。
具体解释看注释:
class Solution {
public:
int countArrangement(int n) {
vector<int> f(1 << n); //开所有状态总数的空间
f[0] = 1;
for (int mask = 1; mask < (1 << n); mask++) { //所有状态
int num = __builtin_popcount(mask);//计算mask中有多少1,也表示在第num位置添加一个数
for (int i = 0; i < n; i++) {//枚举填入数的位置
//mask & (1 << i) 这里是判断 mask 第 i 为是否为 1
//num % (i + 1) == 0 || (i + 1) % num == 0 判断i + 1这个数可不可放到第num这个位置。
if (mask & (1 << i) && (num % (i + 1) == 0 || (i + 1) % num == 0)) {
f[mask] += f[mask ^ (1 << i)]; //加上没放i + 1这个数的方案数
}
}
}
return f[(1 << n) - 1];
}
};
(模拟-简单)学生出勤记录 I
没啥好说的。 题目链接
class Solution {
public:
bool checkRecord(string s) {
int n = s.size();
int num = 0,cnt = 0;
for (int i = 0; i < n; i ++){
if (s[i]=='A')num++;
if (s[i]=='L'&&i < n-2&&s[i+1]=='L'&&s[i+2]=='L')return false;
}
if (num>=2)return false;
else return true;
}
};
(DP - 困难)学生出勤记录 II
和简单题是一样的题目,只不过是问,给定一个n,表示字符串的长度,问有多少种情况可以得到奖励。 题目链接
我的第一反应是组合数学,但是我的组合数学贼垃圾
分析官方给的题解,时间复杂度O(n)(优化我就不讲了,是我太菜了 )
分析:
dp[i][j][k] 表示前i个字符,有j个字符A,有连续k个字符L的所有符合条件的方案数。其中 i ∈ \in ∈ [0,n],j ∈ \in ∈ [0,1],k ∈ \in ∈ [0,2]。
当i = 0时, d p [ 0 ] [ 0 ] [ 0 ] = 1 dp[0][0][0] = 1 dp[0][0][0]=1 ,当 i = 0 时,一定是符合。
当 i ∈ \in ∈ [1,n]三种情况分析
- 当第i个字符为 P 时,也就是到场,则第i天和i-1天,字符A的字符数量不变,连续字符L数量归零。(j ∈ \in ∈ [0,1]),如下:
d p [ i ] [ j ] [ 0 ] = d p [ i ] [ j ] [ 0 ] + ∑ k = 0 2 d p [ i − 1 ] [ j ] [ k ] dp[i][j][0] = dp[i][j][0] + \sum_{k=0}^2dp[i-1][j][k] dp[i][j][0]=dp[i][j][0]+k=0∑2dp[i−1][j][k] - 当第i个字符为A时,也就是缺勤,则第i天和i-1天,字符A的字符数量加1,连续字符L数量归零。j = 0,如下:
d p [ i ] [ j ] [ 0 ] = d p [ i ] [ j ] [ 0 ] + ∑ k = 0 2 d p [ i − 1 ] [ 0 ] [ k ] dp[i][j][0] = dp[i][j][0] + \sum_{k=0}^2dp[i-1][0][k] dp[i][j][0]=dp[i][j][0]+k=0∑2dp[i−1][0][k] - 当第i个字符为L时,也就是迟到,则第i天和i-1天,字符A的数量不变,连续字符L数量加1。j ∈ \in ∈ [0,1],k ∈ \in ∈ [1,2],如下:
d p [ i ] [ j ] [ 0 ] = d p [ i ] [ j ] [ 0 ] + d p [ i − 1 ] [ j ] [ k − 1 ] dp[i][j][0] = dp[i][j][0] + dp[i-1][j][k-1] dp[i][j][0]=dp[i][j][0]+dp[i−1][j][k−1]
const int MOD = 1000000007;
class Solution {
public:
int checkRecord(int n) {
vector<vector<vector<int>>> dp(n + 1, vector<vector<int>>(2, vector<int>(3))); // 长度A的数量,结尾连续 L 的数量
dp[0][0][0] = 1;
for (int i = 1; i <= n; i++) {
// 以 P 结尾的数量
for (int j = 0; j <= 1; j++)
for (int k = 0; k <= 2; k++)
dp[i][j][0] = (dp[i][j][0] + dp[i - 1][j][k]) % MOD;
// 以 A 结尾的数量
for (int k = 0; k <= 2; k++) dp[i][1][0] = (dp[i][1][0] + dp[i - 1][0][k]) % MOD;
// 以 L 结尾的数量
for (int j = 0; j <= 1; j++)
for (int k = 1; k <= 2; k++)
dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k - 1]) % MOD;
}
int res = 0; //长度为n所有情况加起来
for (int j = 0; j <= 1; j++)
for (int k = 0; k <= 2; k++)
res = (res + dp[n][j][k]) % MOD;
return res;
}
};
(模拟-简单)反转字符串中的元音字母
题目:编写一个函数,以字符串作为输入,反转该字符串中的元音字母。题目链接
很简单,唯一的坑点,它数据包含大写和小写。
直接上代码:
class Solution {
public:
string reverseVowels(string s) {
map<int,char> mp;
int n = s.size();
string res = "";
int i,j;
for (i = 0,j = n-1; i < j ;){
while (i < j && !(s[i]=='a'||s[i]=='e'||s[i]=='i'||s[i]=='o'||s[i]=='u'||s[i]=='A'||s[i]=='E'||s[i]=='I'||s[i]=='O'||s[i]=='U')){
res+=s[i];
i++;
}
while (i < j && !(s[j]=='a'||s[j]=='e'||s[j]=='i'||s[j]=='o'||s[j]=='u'||s[j]=='A'||s[j]=='E'||s[j]=='I'||s[j]=='O'||s[j]=='U')) j--;
if (i <= j){
res+=s[j];
mp[j] = s[i];
i ++;
j --;
}
}
for (; i < n; i ++){
if (s[i]=='a'||s[i]=='e'||s[i]=='i'||s[i]=='o'||s[i]=='u'||s[i]=='A'||s[i]=='E'||s[i]=='I'||s[i]=='O'||s[i]=='U'){
if (mp[i]!=NULL)res += mp[i];
else res += s[i];
}else res += s[i];
}
return res;
}
};
(模拟-简单)反转字符串 II
不难题目链接
代码如下:
class Solution {
public:
string reverseStr(string s, int k) {
int n = s.size();
string res = "";
for (int i = 0; i < n; i += 2*k){
int t = n - i;
if (t <= k){
for (int j = n-1; j >= i; j --)res += s[j];
return res;
}
if (k < t && t < 2*k){
for (int j = i + k - 1; j >= i; j --)res += s[j];
for (int j = i + k; j < n; j ++)res += s[j];
return res;
}
for (int j = i + k - 1; j >= i; j --)res += s[j];
for (int j = i + k; j <= i + 2*k-1; j ++)res += s[j];
}
return res;
}
};
(模拟-中等)压缩字符串
题目很好懂,就不讲了,就是压缩字符串的意思。题目链接
有意思的地方是,原字符数组,也是答案的一部分,需要修改原字符数组,而且要使用常量的空间。
class Solution {
public:
int compress(vector<char>& chars) {
int n = chars.size(),res = 0,j = 0,num,cnt;
char t[5]; //用来暂时记录每一位数字
char c;
for (int i = 0; i < n; i ++){
c = chars[i]; //比较字符
num = 1;
chars[j++] = c;
while(++ i < n && chars[i]==c)num++; //计数
cnt = 0;
if (num > 1){
while(num){
res ++;
t[cnt++] = num%10+'0'; //拆数
num/=10;
}
for (int k = cnt-1; k >= 0; k --)chars[j++] = t[k]; //修改chars数组
}
i --;
res ++;
}
return res;
}
};
(数学-中等)逃脱阻碍者
我感觉就是简单题,还达不到中等题。题目链接
就是求给定数组里的坐标和目的坐标欧几里得距离,是否小于原点和目的坐标欧几里得距离,如果小于返回false,如果大于返回true
class Solution {
public:
bool escapeGhosts(vector<vector<int>>& ghosts, vector<int>& target) {
int x = target[0],y = target[1];
int n = ghosts.size();
for (int i = 0; i < n; i ++){
if ((abs(x - ghosts[i][0]) + abs(y - ghosts[i][1])) <= (abs(x)+abs(y)))return false;
}
return true;
}
};
(模拟-简单)获取生成数组中的最大值
简单模拟一下,没有难度 题目链接
class Solution {
public:
int getMaximumGenerated(int n) {
vector<int> num(n+2,0);
if (n==0)return 0;
if (n==1)return 1;
int res = 1;
num[0] = 0;
num[1] = 1;
for (int i = 1; i <= n; i ++){
if (2*i <= n){
num[2*i] = num[i];
res = max(res,num[2*i]);
}
if (2*i+1 <= n){
num[2*i+1] = num[i] + num[i+1];
res = max(res,num[2*i+1]);
}
}
return res;
}
};
(图论-中等)K站中转内最便宜的航班
赤裸裸的模板题。题目链接
Bellman_Ford算法
善于求解有边数限制的最短路求法

官方动态规划题解
下面是Bellman_Ford代码
const int maxn = 10000;
int m,k,dis[110],last[110];
struct Edge{
int x,y,w;
}edges[maxn];
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
m = flights.size();
k++;
for (int i = 1; i <= m; i ++)edges[i] = {flights[i-1][0],flights[i-1][1],flights[i-1][2]};
memset(dis,0x3f,sizeof dis);
dis[src] = 0;
for(int i = 1; i <= k; i++){ //进行k次松弛,就相当于走k条边
memcpy(last,dis,sizeof dis);
for(int j = 1; j <= m; j++){
auto e = edges[j];
dis[e.y] = min(dis[e.y],last[e.x]+e.w); //和dijkstra差不多
}
}
if(dis[dst] > 0x3f3f3f3f / 2)return -1;
else return dis[dst];
}
};
(搜索-中等)所有可能的路径
就是一个赤裸裸的搜索题目链接
我的代码看起来不好看,就不贴了
class Solution {
public:
vector<vector<int>> ans;
vector<int> stk;
void dfs(vector<vector<int>>& graph, int x, int n) {
if (x == n) {
ans.push_back(stk);
return;
}
for (auto& y : graph[x]) {
stk.push_back(y);
dfs(graph, y, n);
stk.pop_back();
}
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
stk.push_back(0);
dfs(graph, 0, graph.size() - 1);
return ans;
}
};
(贪心-中等)救生艇
很简单的贪心,由于题目说一个船只能做两个人,那题目就变得简单了,判断最大的和最小的能不能组合,能就两个人坐一条船,不能就最大的单独坐一条船,一次贪心下去。题目链接
class Solution {
public:
int numRescueBoats(vector<int>& p, int l) {
int res = 0;
sort(p.begin(),p.end());
int le = p.size();
for (int i = 0,j = le - 1; i <= j;){
if (p[j]+p[i]<=l){
i++,j--;
}else j--;
res++;
}
return res;
}
};
(模拟-困难)数据流的中位数
最优解法求中位数。题目链接
双端队列
class MedianFinder {
public:
priority_queue<int, vector<int>, less<int>> queMin; //小顶堆:存放大于中位数的值
priority_queue<int, vector<int>, greater<int>> queMax; //大顶堆:存放小于中位数的值
MedianFinder() {}
void addNum(int num) {
if (queMin.empty() || num <= queMin.top()) { //如果小于等于小顶堆堆首,添加进去
queMin.push(num);
if (queMax.size() + 1 < queMin.size()) { //判断小顶堆的数量是否比大顶堆多2个
queMax.push(queMin.top()); //平衡两个堆,使得两个堆的数量差值为1
queMin.pop();
}
} else {
queMax.push(num);
if (queMax.size() > queMin.size()) {
queMin.push(queMax.top()); //平衡两个堆,使得两个堆的数量相等
queMax.pop();
}
}
}
double findMedian() {
if (queMin.size() > queMax.size()) {
return queMin.top(); //如果小顶堆数量大于大顶堆数量
}
return (queMin.top() + queMax.top()) / 2.0; //两个堆数量相等
}
};
双指针
class MedianFinder {
multiset<int> nums; //有序数组
multiset<int>::iterator left, right; //两个指针
public:
MedianFinder() : left(nums.end()), right(nums.end()) {} //初始化
void addNum(int num) {
const size_t n = nums.size(); //判断有序数组里面的数量
nums.insert(num); //把num加入nums
if (!n) { //如果n = 0
left = right = nums.begin(); //两个指针指向第一个元素
} else if (n & 1) { //如果n为奇数,说明此时两个指针指向同一个地方
if (num < *left) {//如果小于中位数,num加入后一定在加入前中位数前面的位置
left--; //左指针左移
} else {
right++; //右指针右移
}
} else { //偶数
if (num > *left && num < *right) { //num在左右指针中间
left ++; //左指针右移
right --; //右指针左移 两指针指向同一个位置
} else if (num >= *right) { //num大于等于右指针值
left++; //左指针右移 两指针指向同一个位置
} else { //num小于右指针值,可能小于等于左指针值
right--; //右指针左移
left = right; //无论是小于还是等于左指针值,此时都可使两指针指向中位数
}
}
}
double findMedian() {
return (*left + *right) / 2.0;
}
};
(前缀和-简单)一维数组的动态和
题目链接
class Solution {
public:
vector<int> runningSum(vector<int>& nums) {
int n = nums.size();
for (int i = 1; i < n; i ++)nums[i] += nums[i-1];
return nums;
}
};
(前缀和-简单)所有奇数长度子数组的和
题目链接
class Solution {
public:
int sumOddLengthSubarrays(vector<int>& arr) {
int n = arr.size();
for (int i = 1; i < n; i ++)arr[i] += arr[i-1];
vector<int> sum(n+5,0);
for (int i = 1; i <= n; i ++)sum[i] = arr[i-1];
int res = 0;
for (int i = 1; i <= n; i += 2)
for (int j = 1; j + i - 1 <= n; j ++)
res += sum[j+i-1]-sum[j-1];
return res;
}
};
(前缀和+二分-中等)按权重随机选择
说是话我一开始没看懂题目,看懂之后发现就是一道前缀和+二分 的一道题。题意理解
题意: 给定一个数组w[1, 2, 3, 4], 这个数组的的和为 1 + 2 + 3 + 4 = 10. 对应的我们得到 index {0,1,2,3} 的概率为 {1/10, 2/10, 3/10, 4/10}。现在要求用pickIndex()函数,返回一些index,返回的这些index的概率是依据上面的权重来的。
思路: 创建一个全局数组用来记录w数组的前缀和,通过二分判断随机数在哪个区间上,返回那个值。如 [ 0 ] 代 表 1 , [ 1 , 2 ] 代 表 2 , [ 3 , 4 , 5 ] 代 表 3 , [ 6 , 7 , 8 , 9 ] 代 表 4 [0] 代表 1,[1,2] 代表 2,[3,4,5] 代表 3,[6,7,8,9] 代表 4 [0]代表1,[1,2]代表2,[3,4,5]代表3,[6,7,8,9]代表4
class Solution {
public:
vector<int> W;
Solution(vector<int>& w) {
int n = w.size();
W.push_back(w[0]);
for (int i = 1; i < n; i ++){
w[i] += w[i-1];
W.push_back(w[i]);
}
}
int pickIndex() {
int weight = rand() % W.back();
//upper_bound查找第一个大于某个元素的位置
return upper_bound(W.begin(), W.end(), weight) - W.begin();
}
};
(差分前缀和-中等)航班预订统计
题目链接
模 板 题 模板题 模板题
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& a, int n) {
vector<int> sum(n+1,0);
int le = a.size();
for (int i = 0; i < le; i ++){
int x = a[i][0],y = a[i][1],z = a[i][2];
sum[x-1]+=z;
sum[y]-=z;
}
for (int i = 1; i < n; i ++)sum[i] += sum[i-1];
sum.pop_back();
return sum;
}
};