Unit1_2：分治算法

一、主要思想

分：将给定问题分成两个或多个子问题(理想情况下大小大致相等)。
治：解决每个子问题(如果足够小，直接解决或递归解决)。
连：将子问题的解组合成一个全局解。

二、最大连续子数组–MCS

在一串给定数组中，找到一组连续字串使得和最大。

思路

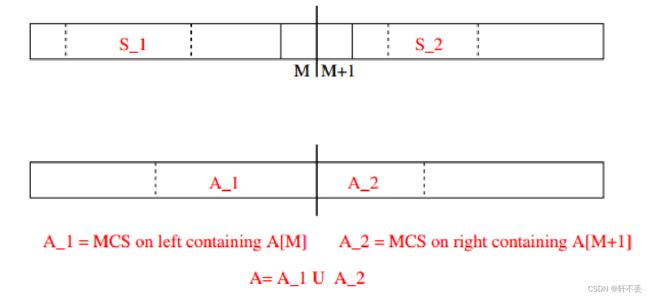
将问题分成一半，此时求的是左边的MCS，右边的MCS以及连接处的MCS。
假设连接处两边字串为$A1$和$A2$，那么需满足
  $A1$是以M结尾的最大字串
  $A2$是以M+1开头的最大字串
求解$A1$和$A2$很简单设为$F(n)$：以$A1$为例，$A2$同理。

MAX ←A[m]
SUM← A[m]
for i← m-1 to 1 do
	SUM ← SUM+A[i]
	if  SUM > MAX then
		MAX ← SUM;
	end
end

计算$A1$时间复杂度为$O(m)$，计算$A2$时间复杂度为$O(n-m)$，因此总时间复杂度为$O(n)$，很小。
综上所述，计算$MCS(n)$的过程即为$MCS(n)=2MCS(n/2)+F(n)$

MCS(A,s,t)
begin
	if s=t then return A[s]
	else
		m ← (s+t)/2
		Find MCS(A,s,n)
		Find MCS(A,m+1,t)
		Find MCS that contains both A[m] and A[m-1](F(A,m))
		return maximum of the three sequences found
end

调用MCS(A,1,n)

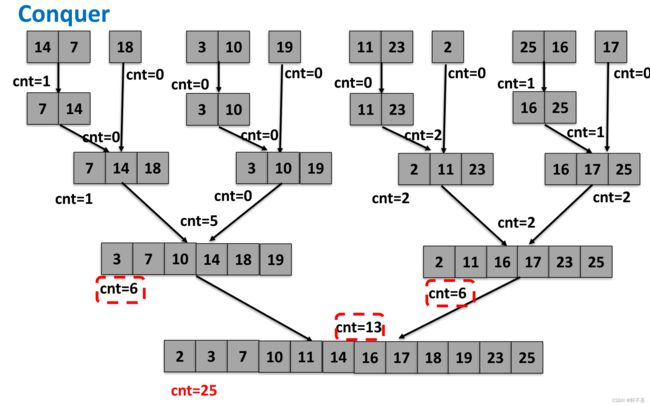
流程分析

时间复杂度

典型的分治算法，时间复杂度：

$T(n)=\{\begin{array}{ll}2T(\frac{n}{2})+n& ifn>1\\ 1& ifn=1\end{array}$
在第一节时提及三种计算方式，最后得出复杂度为$O(nlogn)$

彩蛋

本题还有更快的算法（与本章讲解无关），这种连续求和的问题，首先想到的应该就是前缀和。

在读入数组的时候就可以计算前缀和s[i]，表示前i个数的和。

要求最大得到字串，本质上就是找到$i,j$使得$s[i][-s[j]$的和最大。

因此只要在这些前缀和中找到最大值和最小值，此时
$MAX(s[i])-MIN(s[j])$即为最大连续子数组。

时间复杂度即读入数组时的$O(n)$，每个子操作都是$O(1)$，因为读入数组必然需要花费$O(n)$，因为这个算法最快。

三、逆序计算

思路

分：将数组分成$A$和$B$两部分
治：递归地计数每个数组中的反转
和：对$a\in A,b\in B$的反转$(a,b)$进行计数，记为f(n)

接下来的问题就是如何对f(n)进行计数，因为逆序是A，B之间问题，与A，B内部没有关系，倘若A，B排好序，则技术就会简单许多，当排好序后，问题即可如下解决：
从左到右扫描A和B
比较ai和bj
 如果ai < bj，则ai不与B中剩余的任何元素反向。
 如果ai > bj，则bj与A中剩下的每个元素倒转。
此时因为比较再顺便将序拍好（归并排序）

Merge-and-Count(A, B)
while both A and B are not empty do
	// Let a and b represent the first element of A and B, repectively
	if a

一层循环，时间复杂度为$O(n)$

流程解释

伪代码

if L is empty then
	return 0, L;
end
Divide L into two halves A and B;
(rA, A)←Sort-and-Count(A);
(rB, B)←-Sort-and-Count(B);
(rL, L)←Merge-and-Count(A, B);//O(n)
return

时间复杂度

同样是典型的分治算法，时间复杂度：

$T(n)=\{\begin{array}{ll}2T(\frac{n}{2})+n& ifn>1\\ 1& ifn=1\end{array}$
在第一节时提及三种计算方式，最后得出复杂度为$O(nlogn)$

四、多项式乘法

思路

正常多项式的计算，时间复杂度为$O(n^2)$，下面介绍分治算法。
定义：
  $A_0(x)=a_0+a_{1}x+\dots \dots +a_{\frac{n}{2}-1}{x}^{\frac{n}{2}-1}$
  $A_1(x)=a_{\frac{n}{2}}+a_{\frac{n}{2}+1}x+\dots \dots +a_n{x}^{\frac{n}{2}}$
        $A(x)=A_0(x)+A_1(x)x^{\frac{n}{2}}$
同理，定义：
        $B(x)=B_0(x)+B_1(x)x^{\frac{n}{2}}$

这样，原始问题被分成了4个输入大小为n/2的问题。
$A(x)B(x)=A_0(x)B_0(x)+(A_0(x)B_1(x)+A_1(x)B_0(x))x^{\frac{n}{2}}+A_1(x)B_1(x)x^n$

分治

根据上述思路：
分：计算$A_0(x)B_0(x)$     $A_0(x)B_1(x)$     $A_1(x)B_0(x)$     $A_1(x)B_1(x)$
治：可通过递归算法计算四次
和：计算$A(x)B(x)=A_0(x)B_0(x)+(A_0(x)B_1(x)+A_1(x)B_0(x))x^{\frac{n}{2}}+A_1(x)B_1(x)x^n$

伪代码

$A_0(x)=a_0+a_{1}x+\dots \dots +a_{\frac{n}{2}-1}{x}^{\frac{n}{2}-1}$
$A_1(x)=a_{\frac{n}{2}}+a_{\frac{n}{2}+1}x+\dots \dots +a_n{x}^{\frac{n}{2}}$
$B_0(x)=b_0+b_{1}x+\dots \dots +b_{\frac{n}{2}-1}{x}^{\frac{n}{2}-1}$
$B_1(x)=b_{\frac{n}{2}}+b_{\frac{n}{2}+1}x+\dots \dots +b_n{x}^{\frac{n}{2}}$
$U(x)\leftarrow PolyMultil(A_0(x),B_0(x))$                     $T(\frac{n}{2})$
$V(x)\leftarrow PolyMultil(A_0(x),B_1(x))$                    $T(\frac{n}{2})$
$W(x)\leftarrow PolyMultil(A_1(x),B_0(x))$                   $T(\frac{n}{2})$
$Z(x)\leftarrow PolyMultil(A_1(x),B_1(x))$                    $T(\frac{n}{2})$
$return(U(x)+[V(x)+W(x)]x^{\frac{n}{2}}+Z(x)x^n)$    $O(n)$

时间复杂度

$T(n)=\{\begin{array}{ll}4T(\frac{n}{2})+n& ifn>1\\ 1& ifn=1\end{array}$
根据主定理，$T(n)=O(n^2)$
时间复杂度并没有得到提升，因此考虑优化

优化

考虑计算$A_0(x)B_0(x)$     $A_0(x)B_1(x)+A_1(x)B_0(x)$     $A_1(x)B_1(x)$三个多项式而不是四个
因此设:
$Y=(A_0(x)+A_1(x))(B_0(x)+B_1(x))$
$U=A_0(x)B_0(x)$
$Z=A_1(x)B_1(x)$
因此
$A_0(x)B_1(x)+A_1(x)B_0(x)=Y-U-Z$
伪代码：
$A_0(x)=a_0+a_{1}x+\dots \dots +a_{\frac{n}{2}-1}{x}^{\frac{n}{2}-1}$
$A_1(x)=a_{\frac{n}{2}}+a_{\frac{n}{2}+1}x+\dots \dots +a_n{x}^{\frac{n}{2}}$
$B_0(x)=b_0+b_{1}x+\dots \dots +b_{\frac{n}{2}-1}{x}^{\frac{n}{2}-1}$
$B_1(x)=b_{\frac{n}{2}}+b_{\frac{n}{2}+1}x+\dots \dots +b_n{x}^{\frac{n}{2}}$
$Y(x)\leftarrow PolyMultil(A_0(x)+A_1(x),B_0(x)+B_1(x))$                    $T(\frac{n}{2})$
$W(x)\leftarrow PolyMultil(A_0(x),B_0(x))$                   $T(\frac{n}{2})$
$Z(x)\leftarrow PolyMultil(A_1(x),B_1(x))$                    $T(\frac{n}{2})$
$return(U(x)+[Y(x)-U(x)-Z(x)]x^{\frac{n}{2}}+Z(x)x^n)$    $O(n)$
此时时间复杂度：
$T(n)=\{\begin{array}{ll}3T(\frac{n}{2})+n& ifn>1\\ 1& ifn=1\end{array}$
根据主定理，$T(n)=O(n^{log3})$

彩蛋

分治算法并不总是给你最好的解决方案，我们最初的算法就像蛮力一样糟糕。
多项式乘法中最快是其实是$T(n)=O(nlogn)$，它涉及到使用快速傅里叶变换算法作为子程序。
我们上述做法一个类似的思想是经典的Strassen矩阵乘法算法的基础。