[深度学习入门]PyTorch环境配置与PyTorch学习
目录
- 一.PyTorch简介与环境配置
- 二.PyTorch学习
-
- (一)Torch与Numpy
- (二)张量tensor
- (三)Torch 中的数学运算
- (四)矩阵运算
- (五)利用PyTorch简单地实现几种激活函数
- (六)建造第一个神经网络——关系拟合 (回归)
- (七)快速搭建法
- (八)保存提取
-
- 1.保存并恢复全网络:
- 2.只保存并恢复参数:
- (九)批训练(mini-batch training)
- (十)加速神经网络训练 (Speed Up Training)
-
- 1.SGD(随机梯度下降)
- 2.Momentum(动量法)
- 3. AdaGrad
- 4. RMSProp
- 5. Adam
- 补充:Optimizer 优化器
一.PyTorch简介与环境配置
PyTorch是一个开源的Python机器学习库,是一个相当简洁且高效快速的框架,是Torch在Python上的衍生。
因为Torch是一个使用Lua语言的神经网络库,Torch很好用,但是 Lua 又不是特别流行,所以开发团队将Lua的Torch移植到了更流行的语言——Python上。PyTorch一发布就引起了剧烈的反响。
下载网址:https://pytorch.org/。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第1张图片](http://img.e-com-net.com/image/info8/c680f0c39cd04acfbb403cbe1a186257.jpg)
Anaconda是由Continuum Analytics开发的一款集成了Conda、Python以及一大堆安装好的工具包的开源软件。
其中Conda是一个包、环境管理器,可以用于在同一个机器上安装不同版本的软件包及其依赖,并能够在不同的环境之间切换。
下载网址:https://www.anaconda.com/。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第2张图片](http://img.e-com-net.com/image/info8/fae07ca731024da192f44e7df146a645.jpg)
GPU(可选):一张高性能NVIDIA显卡。
具体安装教程可以参考B站up:我是土堆 的视频BV1hE411t7RN。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第3张图片](http://img.e-com-net.com/image/info8/300f91ab51354df8ade12fc8824e766d.jpg)
IDE推荐:PyCharm
![[深度学习入门]PyTorch环境配置与PyTorch学习_第4张图片](http://img.e-com-net.com/image/info8/744b8090210541e1a0276752a963d4e3.jpg)
自带汉化包插件
可更换Python解释器,这里要选择第二行的Anaconda自带的Python(在这个Python环境中安装了Pytorch框架)。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第5张图片](http://img.e-com-net.com/image/info8/43aac291bb1e45da9f77e749655192af.jpg)
可编辑脚本文件,也可在Python控制台实现交互式编辑
![[深度学习入门]PyTorch环境配置与PyTorch学习_第6张图片](http://img.e-com-net.com/image/info8/1b57375146604b76bdedfd225c1f7d31.jpg)
在下面菜单栏的Python Packages中可以查看本解释器已安装的第三方包。
二.PyTorch学习
(一)Torch与Numpy
Torch 自称为神经网络界的 Numpy, 因为他能将 Torch 产生的 tensor 放在 GPU 中加速运算 (前提是你有合适的 GPU), 就像 Numpy 会把 array 放在 CPU 中加速运算。
所以神经网络的话, 当然是用 Torch 的 tensor 形式数据最好。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第7张图片](http://img.e-com-net.com/image/info8/63e5c92b62414f668fea9c8286c4505b.jpg)
(二)张量tensor
张量tensor分为0维、1维、2维和多维。
0维张量就是标量。
1维张量就是数组。
2维张量就是矩阵。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第8张图片](http://img.e-com-net.com/image/info8/9fa63f6ede17456eacaa3ef3bc4ed432.jpg)
(三)Torch 中的数学运算
(四)矩阵运算
除了简单的计算, 矩阵运算才是神经网络中最重要的部分。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第11张图片](http://img.e-com-net.com/image/info8/41fdcd93deb944caab24f849e0026275.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第12张图片](http://img.e-com-net.com/image/info8/8f75c5ad733d4fb6a1dcf9a765bb4574.jpg)
tensor.dot()是把两个张量的每一对元素都分别对应相乘再相加。
最后结果应该是30.0
(五)利用PyTorch简单地实现几种激活函数
(六)建造第一个神经网络——关系拟合 (回归)
如何在数据当中找到他们的关系, 然后用神经网络模型来建立一个可以代表他们关系的线条。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第16张图片](http://img.e-com-net.com/image/info8/1d9e312b47bf42e786fa29e97095f6b1.jpg)
torch.unsqueeze(input, dim, out=None):起升维的作用,参数dim表示在哪个地方加一个维度,dim范围在:[-input.dim() - 1, input.dim() + 1]之间。比如输入input是一维,则dim=0时数据为行方向扩,dim=1时为列方向扩,再大会出现错误。
tensor.size(x)用于返回tensor第 x 维的长度,不放参数即返回tensor的形状(同tensor.shape)。
torch.rand(x.size()) →随机生成一个与x形状相同的矩阵,取值在(0,1)区间。
1.首先,我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它(如果不加噪声,得到的y仅仅是一条x平方的曲线,而不是一些需要拟合的点)
2.然后,我们建立一个神经网络,这里可以直接运用 torch 中的体系。先定义所有的层属性(init()), 然后再一层层搭建(forward(x))层与层的关系链接。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第17张图片](http://img.e-com-net.com/image/info8/79e7a6bef2ee4f10b1b94bdf05c3a223.jpg)
多少个输入,多少个隐藏层神经元,多少个输出
self.hidden(x) → 使用隐藏层加工一下x,x作为输入经过隐藏层,得到输出为n_hidden。
F.relu() → 用relu激励函数激励n_hidden。
上页搭建的神经网络的结构如下:
![[深度学习入门]PyTorch环境配置与PyTorch学习_第18张图片](http://img.e-com-net.com/image/info8/2f155b81ef5f417280411153045e991b.jpg)
3.接下来,我们开始训练搭建好的神经网络。
损失函数的实例化:

损失函数输入是一个输入的pair(对):(output, target),然后计算出一个数值来评估output和target之间的差距大小;
其中output代表的是神经网络评估出来的输出值yk,>target代表(有监督训练的,真实的)标签tk。
torch.nn中有若干个不同的损失函数可供使用,比如nn.MSELoss就是通过计算均方损失来评估输入和目标值之间从差距【越小越好】
![[深度学习入门]PyTorch环境配置与PyTorch学习_第19张图片](http://img.e-com-net.com/image/info8/ea82b6a006de4d7c884168c26c89d945.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第20张图片](http://img.e-com-net.com/image/info8/c1e0b8664d0145fca3c6e4619632360e.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第21张图片](http://img.e-com-net.com/image/info8/9eb8bcb7cd1c4be5b174901fc00aac71.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第22张图片](http://img.e-com-net.com/image/info8/4aa1a8d4c57b451b93cef92d5622595d.jpg)
(七)快速搭建法

Sequential 本质是一个模块(即 Module),根据Pytorch中的约定,模块中可以继续添加模块。
这意味着我们可以在 Sequential 中添加其它的模块(自然也就可以添加其他的 Sequential)。
添加完成后,Sequential 会将这些模块组成一个流水线,输入将依次通过这些模块得到一个输出。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第23张图片](http://img.e-com-net.com/image/info8/2bfd86d436644d0bb8d3c4d833d7eb8b.jpg)
(八)保存提取
1.保存并恢复全网络:
这种方式很简单,不需要再构造一个网络,直接net2=torch.load(‘net.pkl’)(名字要和保存的一致)。
2.只保存并恢复参数:
这种方式则需要构建一个层数,神经元数一致的网络。
之后再net2.load_state_dict(torch.load(‘net_params.pkl’))即可。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第24张图片](http://img.e-com-net.com/image/info8/d3cf5001f49a49319d2a0ad2f254e286.jpg)
state_dict()将layer_name : layer_param的键值信息存储为dict形式。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第25张图片](http://img.e-com-net.com/image/info8/bdbda19437f146d3af348e4d43e8b9b5.jpg)
load_state_dict是使用反序列化的state_dict加载模型的参数字典,用来加载模型参数。(load_state_dict函数的参数是字典对象,而不是保存对象的路径)
格式:torch.nn.Module.load_state_dict(state_dict, strict=True)
对net123用完全相同的方式训练100步,并进行可视化。
运行程序并验证,发现三张图完全一致。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第26张图片](http://img.e-com-net.com/image/info8/ca5199f1c3a448d9a1f814d4a140640d.jpg)
(九)批训练(mini-batch training)
首先介绍一下import torch.utils.data as Data,这在训练过程中基本都会用到。该接口大多用来读取数据和把数据封装成Tensor,之后的DataLoader用来做mini-batch训练。

DataLoader 是 torch 给我们用来包装数据的工具。
所以要将自己的 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中。使用 DataLoader 的好处是:他们帮你有效地迭代数据。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第27张图片](http://img.e-com-net.com/image/info8/7b15cd8bdca041e8a467fef846f2deb3.jpg)
TensorDataset 基于一系列张量构建数据集。这些张量的形状可以不尽相同,但第一个维度必须具有相同大小。( TensorDataset 将张量的第一个维度视为数据集大小的维度,数据集在传入 DataLoader 后,该维度也是 batch_size 所在的维度)
实际上还有第五个参数drop_last: 当样本数不能被batchsize整除时, 是否舍弃最后一批数据。(默认不舍弃)
DataLoader构建可迭代的数据装载器,我们在训练的时候,每一个for循环,每一次iteration(迭代),就是从DataLoader中获取一个batch_size大小的数据的。
Epoch: 所有训练样本都已输入到模型中,称为一个Epoch。
Iteration(step): 一批样本输入到模型中,称为一个Iteration。
Batchsize: 一批样本的大小, 决定一个Epoch有多少个Iteration。
例:假设样本总数80, Batchsize是8, 那么1Epoch=10Iteration。 假设样本总数是87, Batchsize是8, 如果drop_last=True, 那么1Epoch=10Iteration;如果等于False, 那么1Epoch=11Iteration, 最后1个Iteration有7个样本。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第28张图片](http://img.e-com-net.com/image/info8/96336eca85d74c8cabc003beca872d49.jpg)
enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标。
输出结果如下:
![[深度学习入门]PyTorch环境配置与PyTorch学习_第29张图片](http://img.e-com-net.com/image/info8/7dec88fc00fa4450a77c60dd2325627e.jpg)
若将BATCH_SIZE改为8,则结果如下:

多次运行上述代码,发现结果均一致,而不是随机的。
这是因为我们在程序开头加入了这句:
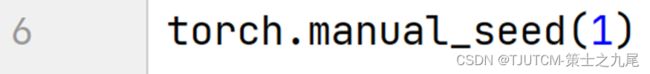
torch.manual_seed()手动设置种子,一般可用于固定随机初始化的权重值(一旦固定种子,后面依次生成的随机数其实都是固定的)
这样就可以让每次重新训练网络时的权重的初始值虽然是随机生成的,但结果却是固定的。
(十)加速神经网络训练 (Speed Up Training)

深度学习的优化算法主要有GD,SGD,Momentum,RMSProp和Adam算法等。
深度学习中绝大多数目标函数都很复杂。因此,很多优化问题并不存在解析解,而需要使用基于数值方法的优化算法找到近似解,即数值解。以下讨论的优化算法都是这类基于数值方法的算法。
1.SGD(随机梯度下降)
如果使用梯度下降(GD),每次自变量迭代的计算开销为O(n),它随着n线性增长。因此,当训练数据样本数很大时,梯度下降每次迭代的计算开销很高。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第30张图片](http://img.e-com-net.com/image/info8/7d4dc1ba536447358e356527d7da25ae.jpg)
而随机梯度下降(stochastic gradient descent,SGD)减少了每次迭代的计算开销。在随机梯度下降的每次迭代中,我们随机均匀采样的一个样本索引i∈{1,…,n},并计算梯度∇fi(x)来迭代x。于是每次迭代的计算开销从梯度下降的O(n)降到了常数O(1)。
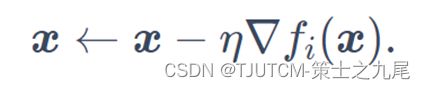
我们还可以在每轮迭代中随机均匀采样多个样本来组成一个小批量,然后使用这个小批量来计算梯度。称为小批量随机梯度下降。通常,小批量随机梯度在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。

2.Momentum(动量法)
在SGD的每次迭代中,梯度下降根据自变量当前位置,沿着当前位置的梯度更新自变量。然而,如果自变量的迭代方向仅仅取决于自变量当前位置,这可能会带来一些问题。
同一位置上,目标函数在竖直方向比在水平方向的斜率的绝对值更大。因此,给定学习率,梯度下降迭代自变量时会使自变量在竖直方向比在水平方向移动幅度更大。
动量法依赖指数加权移动平均(exponentially weighted moving average)使得自变量的更新方向更加一致,从而降低发散的可能。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第31张图片](http://img.e-com-net.com/image/info8/028ca9522b244cdd8ce08c0dc94fd786.jpg)
其中,动量超参数γ满足0≤γ<1。当γ=0时,动量法等价于小批量随机梯度下降。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第32张图片](http://img.e-com-net.com/image/info8/62765c8edd2040e483a071daea421d45.jpg)
3. AdaGrad
AdaGrad算法根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率,并让目标函数自变量中每个元素都分别拥有自己的学习率,从而避免统一的学习率难以适应所有维度的问题。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第33张图片](http://img.e-com-net.com/image/info8/21b7b305e8134f1abc0b0ecc5837d025.jpg)
ϵ是为了维持数值稳定性而添加的常数,如10−6。
因为调整学习率时分母上的变量st一直在累加按元素平方的小批量随机梯度,所以目标函数自变量每个元素的学习率在迭代过程中一直在降低(或不变)。因此,当学习率在迭代早期降得较快且当前解依然不佳时,AdaGrad算法在迭代后期由于学习率过小,可能较难找到一个有用的解。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第34张图片](http://img.e-com-net.com/image/info8/6a7e789d43c6498eb8882f324b2332e9.jpg)
4. RMSProp
![[深度学习入门]PyTorch环境配置与PyTorch学习_第35张图片](http://img.e-com-net.com/image/info8/9f42a7e34a584193a0f9ab61e71fb2fe.jpg)
RMSProp算法对AdaGrad算法做了一点小小的修改。
不同于AdaGrad算法里状态变量st是截至时间步t所有小批量随机梯度gt按元素平方和,RMSProp算法将这些梯度按元素平方做指数加权移动平均。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第36张图片](http://img.e-com-net.com/image/info8/b0ec18d2301b45ff8deb3d9b6ffa4013.jpg)

RMSProp同时具备Momentum& AdaGrad两种方法的优势。
但我们还没把 Momentum合并完全, RMSProp 缺少了 Momentum 中的红框部分。
5. Adam
![[深度学习入门]PyTorch环境配置与PyTorch学习_第37张图片](http://img.e-com-net.com/image/info8/522f7cb29a4c4f6a83a90695611e3215.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第38张图片](http://img.e-com-net.com/image/info8/96e751f776e847b3952294f77d47627d.jpg)
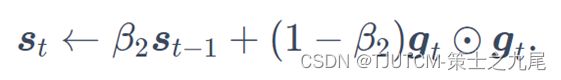




Adam方法的基本思路更像是融合Momentum和AdaGrad二者的优点, Adam算法在RMSProp算法的基础上对小批量随机梯度也做了指数加权移动平均。
Adam的优点主要在于经过偏置校正(使过去各时间步小批量随机梯度权值之和为1)后,每一次迭代学习率都有个确定范围,使得参数比较平稳。
大多数时候, 使用 Adam 都能又快又好的达到目标, 迅速收敛。
![[深度学习入门]PyTorch环境配置与PyTorch学习_第9张图片](http://img.e-com-net.com/image/info8/45ce594ca01440dea2cb5aa1f4941579.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第10张图片](http://img.e-com-net.com/image/info8/37fcee85626143a98071e1b2098067be.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第13张图片](http://img.e-com-net.com/image/info8/60f3d0d0a5f8463abe50877b034b33fb.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第14张图片](http://img.e-com-net.com/image/info8/899d93c2436144f69643f91ce21ea837.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第15张图片](http://img.e-com-net.com/image/info8/64aabd189abc4df8a86204cf0a554368.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第39张图片](http://img.e-com-net.com/image/info8/cdff47447f294a808d2abe0547ae6b40.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第40张图片](http://img.e-com-net.com/image/info8/f48d25c49b9143058ddc1bc2918279e9.jpg)
![[深度学习入门]PyTorch环境配置与PyTorch学习_第41张图片](http://img.e-com-net.com/image/info8/ed61becd9c7848bd870645e07a15fc50.jpg)