Redis中的Zset类型
目录
Zset的相关命令
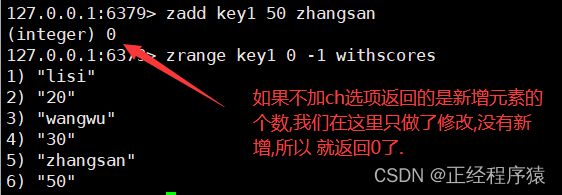
zadd
zrange
zcard
zcount
zrevrange
zrangebyscore
zpopmax
bzpopmax
zpopmin和bzpopmin
zrank
zrevrank
zscore
zrem
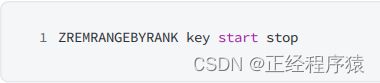
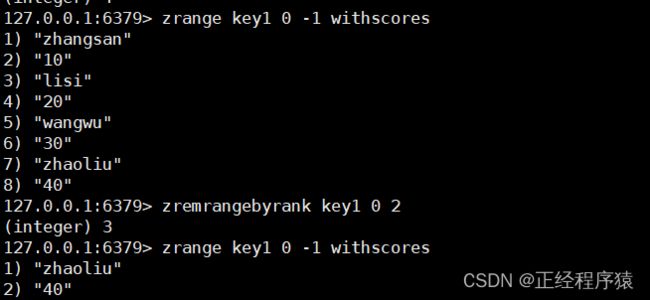
zremrangebyrank
zremrangebyscore
操作集合间的命令
zinterstore和zunionstore
内部编码
Zset的应用场景
Zset表示有序集合的意思.
有序集合保留了集合不能有重复元素的特性,同时,有序集合里的元素总是以升序排列的.
说到排序,要指定一个排序的规则,zset为了实现排序规则,给zset中的member同时引入了一个属性-分数(score),浮点类型.每个member都会安排一个分数.进行排序的时候,就是依照此处的分数大小来进行升序排序的.
zset中的元素是唯一的,但是分数可以重复.
Zset的相关命令
zadd
添加或者更新指定的元素以及关联的分数到zset中,分数应该符合double类型.+inf/-inf作为正负数极限也是合法的.
member和score称为是一个pair.不要把member和score理解成键值对.键值对中是有明确的角色区分的,谁是键谁是值是明确的,一定是根据键来找到对应的值.而对于有序集合来说,既可以通过member找到对应的score,又可以通过score找到匹配的member.
我们在添加的时候既要添加member也要添加分数,而且是分数在前,member在后.
XX:member存在才更新元素,不会添加新的元素.
NX:member不存在才创建新的member,不会更新已经存在的member.
不加XX或者NX:如果当前member不存在,此时就会达到添加新member的效果;如果member已经存在,此时就会更新分数.
LT:less than的缩写,member已经存在,如果更新分数,新的分数比旧的分数小,此时就更新成功,否则就不更新.member不存在,就创建member.
GT:greater than的缩写,member已经存在,如果更新分数,新的分数比旧的分数要大,此时就更新成功,否则就不更新.member不存在,就创建新的member.
CH:zadd本来只返回新增的元素个数,加上CH,就会将改变的member也算上.
INCR:对member的分数加上对应值.如果member不存在,默认其原始的分数为0,并且创建member.
当使用incr的时候,此条命令只能针对一个member-score使用,不能同时操作多组了.
时间复杂度是O(logN).之前hash,set,list很多时候添加一个元素都是O(1).此处的zset是logN,是因为zset是有序结构,要求新添加的元素要放到合适的位置上,找到合适的位置时间复杂度就是logN.
之所以是logN不是N,也是充分利用了有序这样的特点.
当多个元素的分数相同时,它们会按照member的字典序进行排序.
zrange
查看有序集合中的元素详情.
类似于lrange,可以指定一对下标构成的区间.
因为有序集合本身就是有先后顺序的,谁在前谁在后都是明确的,因此也就可以给这个有序集合赋予下标这样的概念了.
当前的查询结果就是按照升序来排列的.
如果修改的分数,影响到了之前的顺序,就会自动的移动元素的位置,保持原有的升序顺序不变.
时间复杂度为O(log(N)+M),N为集合中总的元素个数,M为区间内的元素个数.
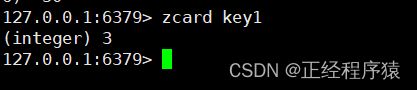
zcard
zcard key用来获取一个zset的基数,即zset中的元素个数.
返回的是zset中的元素个数.
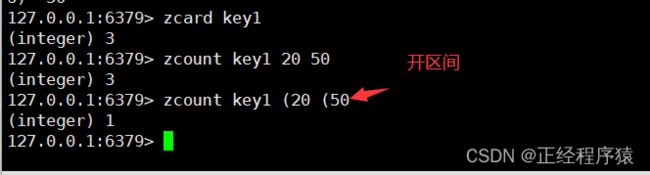
zcount
返回分数在min和max之间的元素个数,默认情况下,min和max都是包含的.如果想要排除边界值,可以加上括号(.
时间复杂度是O(logN).
zcount先根据min找到对应的元素,此时时间复杂度为logN;在根据max找到对应的元素,花费logn.再根据下标做减法,就知道区间里有几个元素了.没有去遍历区间里的元素,所以总的时间复杂度为O(logN).
注意这里的min和max也可以写成浮点数,因为zset中的分数本身就是浮点数.
zrevrange
rev->reverse代表逆序的意思,此时就是按照分数的降序进行遍历并打印了.
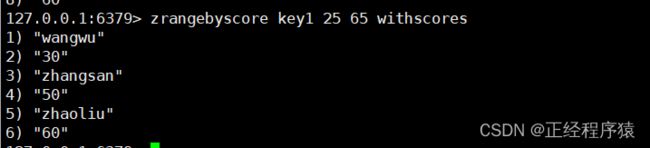
zrangebyscore
按照分数来找元素,和刚才的zcount类似.
时间复杂度是O(log(N)+M).
此命令将在未来的版本中废弃(当前为redis5),并且功能将合并到zrange中.
zpopmax
删除并返回分数最高的count个元素.
返回值就是被删除的元素,包括member和score.
如果存在多个元素的分数相同,同时为最大值,此时zpopmax删除的时候,仍然只删除其中一个元素.
因为分数相同会按照member字符串的字典序来决定先后,所以总有一个顺序.
时间复杂度为O(log(N)*M).
N是有序集合的总的元素个数,M是要删除的元素个数.
此处的删除最大值就相当于是尾删,其实redis内部针对有序集合是记录了尾部这样的位置,那我们就可以通过O(1)的时间复杂度来找到这个元素.但是redis内部并没有这样实现,而是根据member的值进行查找找到位置后在删除.
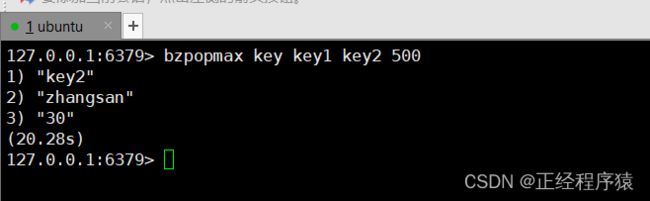
bzpopmax
这是一个带有阻塞功能的命令.
我们的有序集合可以视为是一个优先级队列,有的时候,也需要一个带有阻塞功能的优先级队列.
每个key都是一个有序集合,阻塞也是在有序集合为空的时候触发,一直阻塞到其他客户端往有序集合中插入元素或者超过了阻塞的最大时间.
如果有序集合中有元素了,直接就能返回了,就不会阻塞了.
timoout表示超时时间,最多阻塞多长时间,单位是s,支持小数形式,写作0.1就表示100ms.
时间复杂度为O(logN),删除最大值所需要花费的时间.
注意这里的时间复杂度不是O(log(N)*M),M表示监听的key的个数.虽然监听了多个key,但是我们最终只需要在这多个key中删除一个最大值即可,而不是每个key里都删除一次,所以时间复杂度为logN.
zpopmin和bzpopmin
这两条命令的和上述的zpopmax和bzpopmax逻辑是一致的.只不过是删除有序集合中最小的元素.
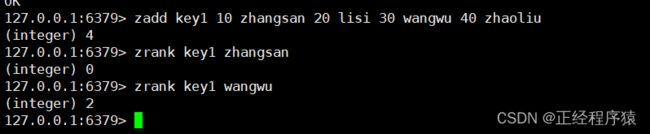
zrank
返回指定元素的排名,升序.
时间复杂度是O(logN).
zrank得到的下标是从前往后算的,升序.
排名是从0开始的.
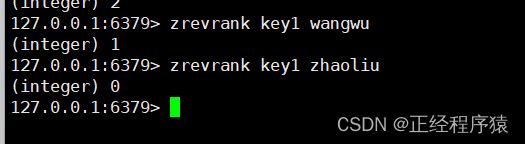
zrevrank
也是获取member的下标,但是下标是反着算的,从后往前.
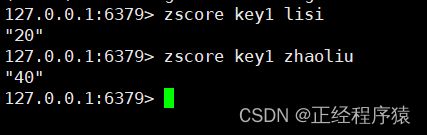
zscore
返回指定元素的分数.
根据member查找分数.
时间复杂度为O(1).此处redis对于这样的查询操作做了优化,付出了额外的空间代价,针对这里的时间复杂度又滑到了O(1).
zrem
删除指定的元素.
返回的是本次操作删除的元素个数.
时间复杂度为O(log(N)*M),N为有序集合中的元素个数,M为要删除的元素个数.
zremrangebyrank
按照升序,删除指定范围内的元素,闭区间.
O(log(N)+M),N是整个有序集合的元素个数,M是区间内的元素个数.
此处查找位置,只需要进行一次,不需要重复进行.
zremrangebyscore
指定一个删除的区间,通过分数来描述.默认是闭区间,可以用(排除边界值.
时间复杂度O(log(N)+M).
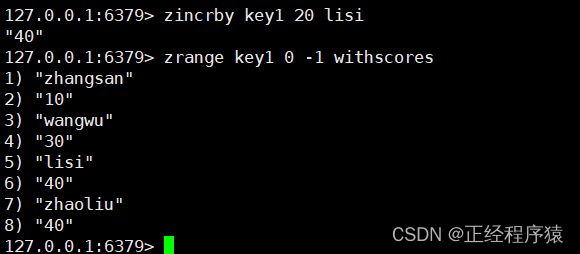
zincrby
为指定的元素的关联分数添加指定的分数值.
返回的是增加后元素的分数.
时间复杂度为O(logN).
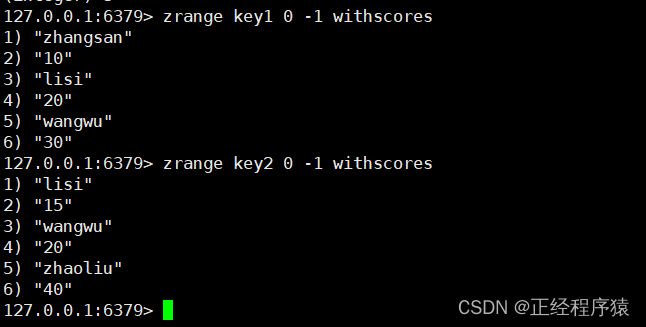
操作集合间的命令
zinter,zunion,zdiff这几个命令是从redis6.2开始支持的,redis5支持的命令有zinterstore和zunionstore.
zinterstore:求交集,结果保存到另一个key中.
zunionstore:求并集,结果保存到另一个key中.
zinterstore和zunionstore
destination:要把结果保存到那个key对应的zset中.
numkeys:是一个整数,描述了后续有几个key参与交集运算.
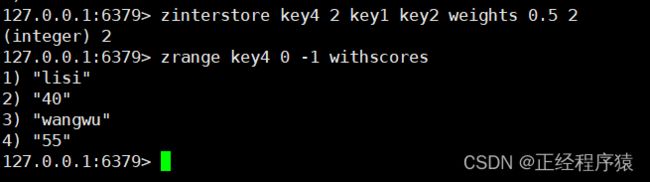
weights:权重,此处的集合是有序集合,每一个member都带有分数,此处指定的权重就相当于一个系数,在集合间进行操作的时候,会让有序集合中的member的分数乘上对应的权重.
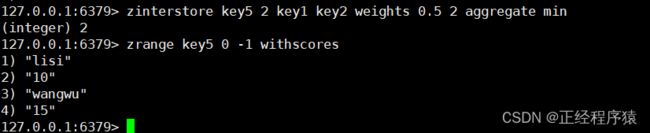
aggregate:表示最终结果集合中的分数是如何计算的,sum表示分数加和,min表示取最小的分数,max表示取最大的分数.
时间复杂度:
这里的时间复杂度如何计算取决于redis源码是如何实现上述求交集操作的.
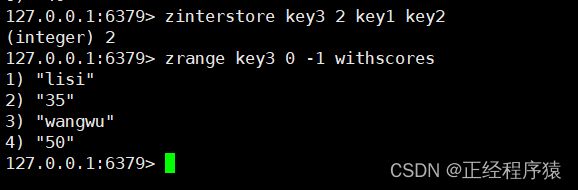
当不加任何选项的时候,默认权重都是1,计算结果分数用的是各分数的和.
加上权重的效果如上.
加上aggregate的效果如上.
zunionstore和zinterstore用法一致,只是zunionstore求的是并集.
时间复杂度:
内部编码
有序集合的内部编码有两种,压缩列表和跳表.
ziplist当有序集合的元素个数⼩于 zset-max-ziplist-entries 配置(默认 128 个), 同时每个元素的值都⼩于 zset-max-ziplist-value 配置(默认 64 字节)时,Redis 会⽤ ziplist 来作为有序集合的内部实现,ziplist 可以有效减少内存的使⽤。
skiplist:当 ziplist 条件不满⾜时,有序集合会使⽤ skiplist 作为内部实现,因为此时 ziplist 的操作效率会下降。
Zset的应用场景
Zset最关键的应用场景就是排行榜系统,例如微博热搜,游戏天梯排行,成绩排行等等.
这类排行榜的关键要点是用来排行的"分数"要求是实时变化的.
使用zset来完成上述操作就非常契合了.
比如游戏天梯排行,只需要把玩家信息和对应的分数给放到有序集合当中即可.此时就自动形成了一个排行榜,随时可以按照排行(下标),按照分数来进行范围查询.随着分数发生改变,也可以比较方便的通过incrby命令来修改分数,排行顺序也会自动调整.
对于要综合考虑各个维度的排行榜,比如微博热搜榜,我们可以使用有序集合间的命令来完成.
比如微博热度要综合考虑浏览量,点赞量,转发量和评论量,此时我们可以把这些都用有序集合来表示.
根据每个维度来计算综合得分,给不同的维度赋予不同的权重,此时就可以借助zinterstore或者zunionstore的加权方式来处理了.