最小哈希Min-hashing理解

最小哈希Min-hashing理解

1. Jaccard

​ 自然文本可以表示成集合，而集合又可以表示成高维的数据，集合除了表示文本，还可以表示图中的顶点。对于集合来说，应用较为广泛的距离或者相似度度量为Jaccard距离或者Jaccard相似度。给定两个集合A和B，两者之间的Jaccard 相似度和距离定义如下:

• Jaccard相似度：

$$Jaccard(A,B)=\frac{|A\cap B|}{|A\cup B|}$$

• Jaccard距离：

$$DJ(A,B)=1-\frac{|A\cap B|}{|A\cup B|}$$

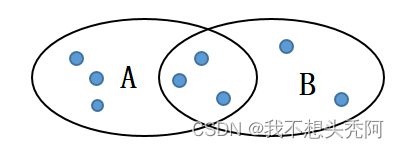
例子：下图中，集合A和集合B的交集大小为3，并集大小为8。因此
$$Jaccard(A,B)=\frac{3}{8}，DJ(A,B)=1-\frac{3}{8}=\frac{5}{8}$$

2. Shingling

​ Shingling是自然语言处理领域中用于衡量两个文档相似度的技术。将一篇文档视为一个字符串，文档的k-Shingling定义为其中任意长度为k的子串。这样，每篇文档便可用文档中出现至少一次 k-Shingling 的集合或包来表示。注意，**集合与包的区别在于集合中的元素只能出现一次，而包中的元素可以出现任意次。**在得到某两篇文档的Shingling表示后，可基于该表示采用Jaccard来衡量两篇文档的相似度。

---

例子：假设一篇文档D的内容为“abcdabcf”。

• 文档D所有2-Shingling组成的包为
  $$S(D)=\{ab,bc,cd,da,ab,bc,cf\}$$

• 文档D所有2-Shingling组成的集合为
  $$S(D)=\{ab,bc,cd,da,cf\}$$

​ k大小的选择对最终的结果影响很大。例如，当k=1时，由于每篇文档都会包含大量的常用字，因此会得到很多Jaccard相似度很高的文档对;而当k太大，会导致每篇文档只有很少的k-Shingling存在交集，即几乎所有文档之间Jaccard相似度为0。因此，k大小的选择依赖于文档的典型字符的长度，其值应当能保证任意给定的Shingling 出现在任意文档中的概率较低。

---

3. Min-hashing

​ 给定布尔向量 v 和随机排列 h ，h(v)为布尔向量v经过随机排列后得到的新向量，mh(v)为新得到的布尔向量h(v)中第一个不为0的行号，函数mh(v)被称之为最小哈希函数。

定义	含义
v	布尔向量
h	随机排列
h(v)	v经过随机排列后得到的新向量
mh(v)	h(v)中第一个不为0的行号

---

例子：给定如下四篇文档，求各文档的最小哈希值

文档	内容
d1	“数据 科学 真 是 有趣”
d2	”数据 科学“
d3	“科学 真 是 有趣”
d4	“数据 科学 是 有趣”

①先求出2-Shingling的特征矩阵，分为以下三个步骤：

• 步骤1：求出每篇文档分词后的2-Shingling集合，这里分词的策略是按照空格进行划分

文档	2-Shingling集合
d1	{数据 科学、科学 真、真 是、是 有趣}
d2	{数据 科学}
d3	{科学 真， 真 是，是 有趣}
d4	{数据 科学、科学 是、是 有趣}

• 步骤2：利用哈希函数将2-Shingling集合中的元素映射为其对应的桶号：
  $$\begin{gathered} h(数据科学)=0 \\ h(科学真)=1 \\ h(真是)=2 \\ h(是有趣)=3 \\ h(科学是)=4 \end{gathered}$$

  ---

  $$\begin{gathered} d_1=\{0、1、2、3\} \\ {d}_2=\{0\} \\ {d}_3=\{1、2、3\} \\ {d}_4=\{0、4、3\} \end{gathered}$$

• 建立出特征矩阵

桶编号	d1	d2	d3	d4
0	1	1	0	1
1	1	0	1	0
2	1	0	1	0
3	1	0	1	1
4	0	0	0	1

②对特征矩阵进行行重排，得到如下的矩阵

桶编号	d1	d2	d3	d4
4	0	0	0	1
1	1	0	1	0
3	1	0	1	1
2	1	0	1	0
0	1	1	0	1

​ 各文档的最小哈希值为
$$\begin{gathered} mh(d_1)=1 \\ mh(d_2)=4 \\ mh(d_3)=1 \\ mh(d_4)=0 \end{gathered}$$

---

定理：两个集合S1和S2经过多次随机排列之后得到的两个最小哈希值相等的概率等于这两个集合的Jaccard相似度，即
$$Pr[mh(S_1)=mh(S_2)]=Jaccard(S_1,S_2)$$

3.1 最小哈希签名

​ 随机选择n个排列变换用于对特征矩阵进行随机重排，对集合S，将会得到n个最小哈希值。集合S的最小哈希签名即为n个最小哈希值构成的列向量
$$(m{h}_1(S),m{h}_2(S),...,m{h}_n(S))$$
​ 由多个集合的最小哈希签名构成的矩阵即为最小哈希签名矩阵。

​ 对特征矩阵进行随机行排列变换可以通过一个随机的哈希函数来模拟，该哈希函数可将特征矩阵的行号映射到与矩阵行数相同的桶中。具体地，将原来的第r行放在随机排列变换后第h®的位置上。至此，可以随机选取$h_1,h_2,...,h_n$模拟n次随机行排列变换。

---

​ 例子：给定两个用于代替行排列变换的哈希函数$h_1(x)=(x+1)mod5$和$h_2(x)=(3x+1)mod5$，求出上文中的特侦矩阵对应的最小哈希签名矩阵。

​ 首先计算两个哈希函数对行号映射的结果

行号	d1	d2	d3	d4	(x+1) mod 5	(3x+1) mod 5
0	1	1	0	1	1	1
1	1	0	1	0	2	4
2	1	0	1	0	3	2
3	1	0	1	1	4	0
4	0	0	0	1	0	3

哈希函数$(x+1)mod5$表示第0行经过行重排将被映射到第1行，第1行经过行重排将被映射到第2行

​ 根据最小哈希签名的定义可知：
$$m{h}_1(d_1)=1,m{h}_1(d_2)=1,m{h}_1(d_3)=2,m{h}_1(d_4)=0$$
​ 和
$$m{h}_2(d_1)=0,m{h}_2(d_2)=1,m{h}_2(d_3)=0,m{h}_2(d_4)=0$$
​ 则最小哈希签名矩阵为：

	d1	d2	d3	d4
h1	1	1	2	0
h2	0	1	0	0

​ 因此，$d_1$和$d_2$基于最小哈希签名的相似度$Jaccard(d_1,d_2)=\frac{\{1,0\}\cap \{1,1\}}{\{1,0\}\cup \{1,1\}}=\frac{1}{2}$（这里写的不太严谨）

3.2 基于最小哈希签名的相似度

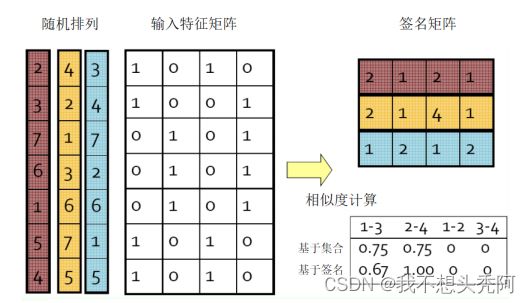
​ 基于最小哈希签名矩阵可以估算文档的相似度。如下图所示，左侧彩色竖条为混排后桶号对应的位置(注意:桶编号和文档编号均从1开始编号)。其对应的最小哈希签名矩阵为右上角。右下角的矩阵中第一行为文档间的Jaccard 相似度，第二行为基于最小哈希签名矩阵计算出的文档相似度。虽然用最小哈希签名矩阵可以近似估算两个集合的相似度，但是当哈希函数个数较少时，估算误差可能会比较大。因此，需要选择恰当数量的哈希函数来降低估算误差。

参考书籍：高明 胡卉芪《数据科学与工程算法基础》